2.4 二次函数的应用 同步练习题(无答案)2022-2023学年北师大版九年级数学下册
文档属性
| 名称 | 2.4 二次函数的应用 同步练习题(无答案)2022-2023学年北师大版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 11:07:28 | ||
图片预览


文档简介
2.4 二次函数的应用 同步练习题2022-2023学年北师大版九年级数学下册
一、选择题
1.用一条长为40 cm的绳子围成一个面积为S cm2的矩形,则S的值不可能为 ( )
A.20 B.40 C.100 D.120
2.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价金额x(元)之间满足函数关系式y=-2x2+60x+800,则获利最多为 ( )
A.15元 B.400元 C.800元 D.1 250元
3.如图,在长为20 m、宽为14 m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1 m,则花圃中的阴影部分有 ( )
A.最小面积,为247 m2 B.最小面积,为266 m2
C.最大面积,为247 m2 D.最大面积,为266 m2
4.如图,某农场拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1 m宽的门,已知现有材料可建墙体(不包括门)的总长为27 m,则能建成的饲养室的最大面积为(墙体的厚度忽略不计) ( )
A.75 m2 B. m2
5.某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售单价为25元时平均每天能售出8件,当销售单价每降低2元时,平均每天能多售出4件,为使该服装店平均每天的销售利润最大,则每件的定价应为 ( )
A.21元 B.22元 C.23元 D.24元
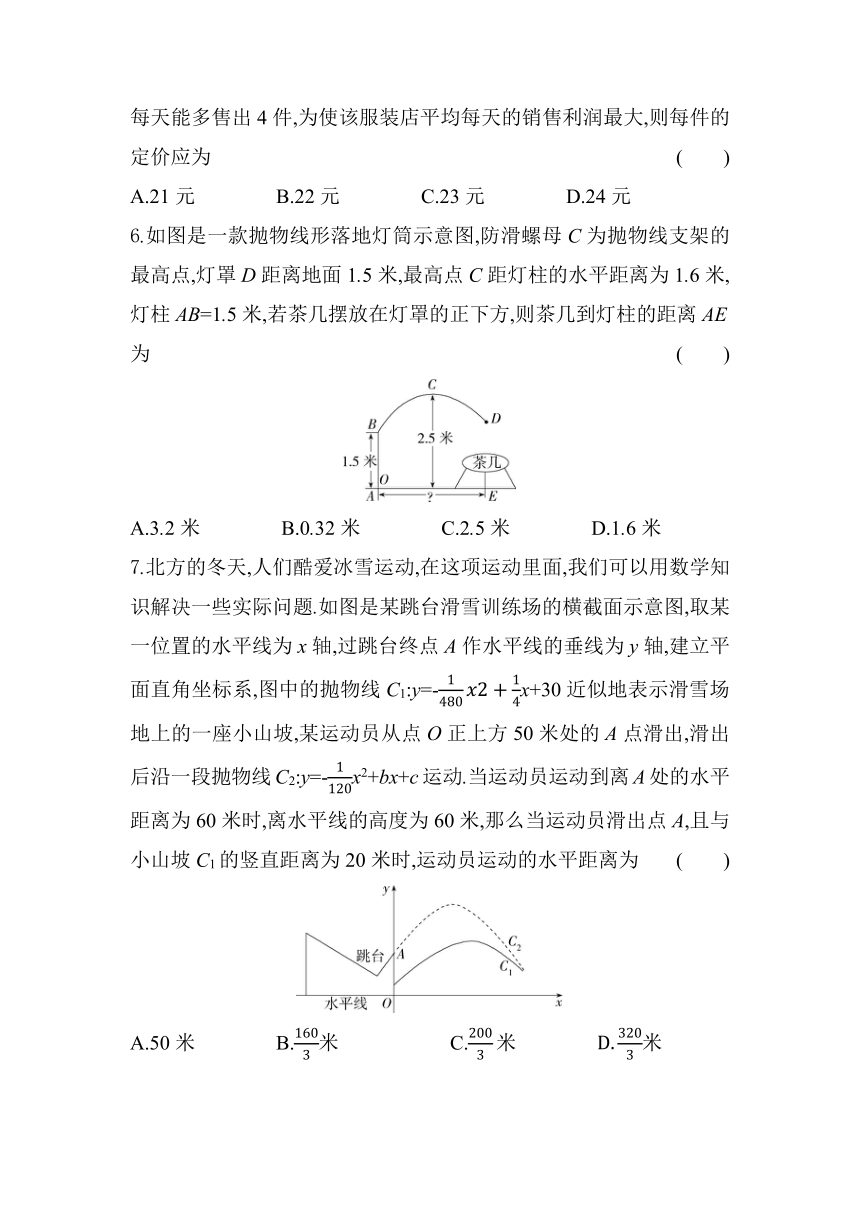
6.如图是一款抛物线形落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB=1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为 ( )
A.3.2米 B.0.32米 C.2.5米 D.1.6米
7.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=-x+30近似地表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线C2:y=-x2+bx+c运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米,那么当运动员滑出点A,且与小山坡C1的竖直距离为20米时,运动员运动的水平距离为 ( )
A.50米 B.米 C.米
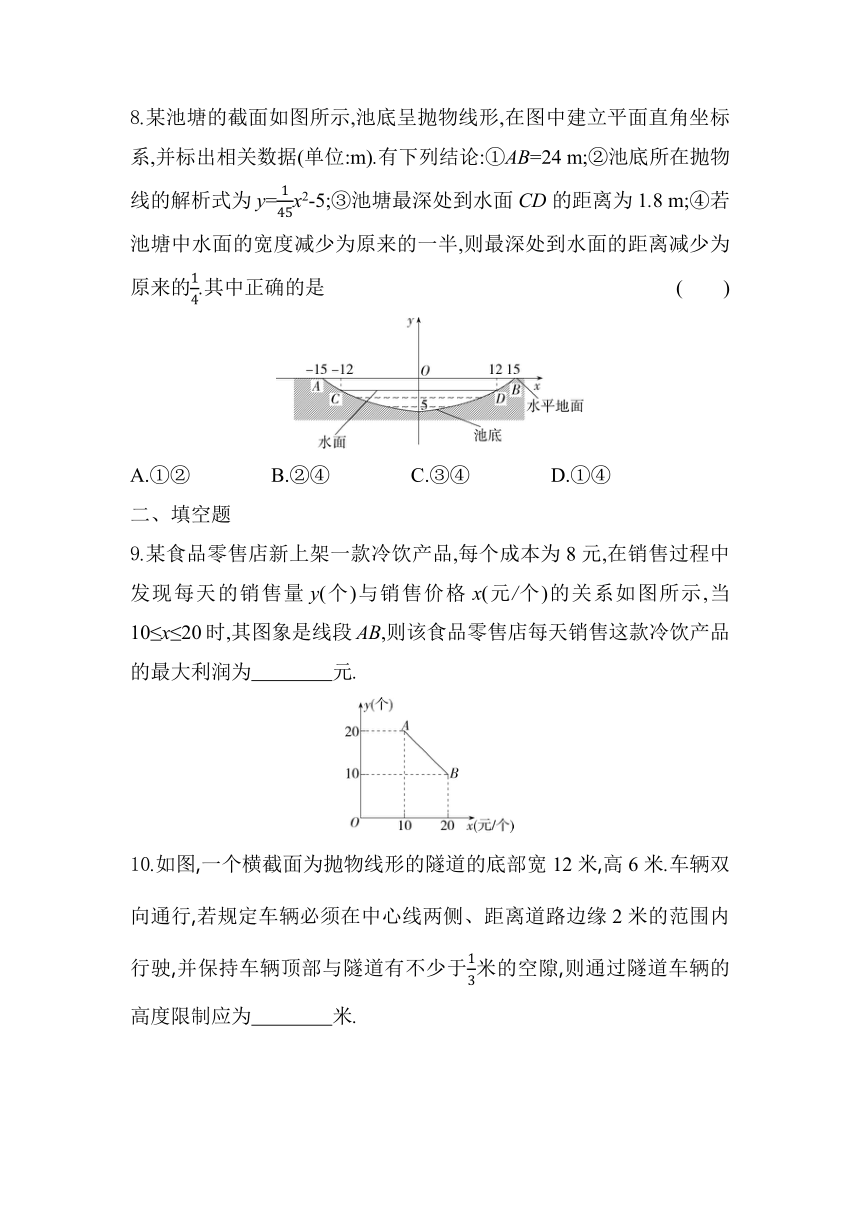
8.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:①AB=24 m;②池底所在抛物线的解析式为y=x2-5;③池塘最深处到水面CD的距离为1.8 m;④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的.其中正确的是 ( )
A.①② B.②④ C.③④ D.①④
二、填空题
9.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中发现每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为 元.
10.如图,一个横截面为抛物线形的隧道的底部宽12米,高6米.车辆双向通行,若规定车辆必须在中心线两侧、距离道路边缘2米的范围内行驶,并保持车辆顶部与隧道有不少于米的空隙,则通过隧道车辆的高度限制应为 米.
11.北仑梅山所产的草莓柔嫩多汁,芳香味美,深受消费者喜爱.有一草莓种植大户,每天草莓的采摘量为300千克,当草莓的零售价为22元/千克时,刚好可以全部售完.经调查发现,零售价每上涨1元,每天的销量就减少30千克,而剩余的草莓可由批发商以18元/千克的价格统一收购,则当草莓零售价为
元/千克时,该种植户一天的销售收入最大.
三、解答题
12.2022年春,新型冠状病毒在多地区肆虐,为方便快捷确保安全,某医疗公司设计了核酸检测小屋,如图所示的是小屋的底面示意图.
设计要求小屋的高为2.4 m,现在有长2.4 m,宽1.2 m的板材20块,制作了内墙(门窗不计).求这个核酸检测小屋的最大占地面积.
13.2022年,疫情导致各行业实体店均面临前所未有的挑战,为了刺激消费,各商场对某些商品降价销售,其中鲜猪肉进价为每千克16元,当销售价为30元/千克时,每天能售出200千克,当售价每千克每降低2元时,平均每天可多售出40千克,当售价为多少时,每天的销售利润最大
14.三分线到篮球筐中心的水平距离为7 m,在三分线上投篮,刚好命中篮球筐中心.如图,篮球运动的路线可看成是抛物线y=-x2+bx+c的一部分.
(1)求抛物线的解析式;
(2)求这次投球的最高点的高度.(结果保留整数)
15.“八婺”菜场指导菜农生产和销售某种蔬菜,提供如下信息:
①统计售价与需求量的数据,发现该蔬菜需求量y需求(吨)关于售价x(元/千克)的函数图象可以看成抛物线,其表达式为y需求=ax2+c,部分对应值如下表:
售价x (元/千克) … 2.5 3 3.5 4 …
需求量 y需求(吨) … 7.75 7.2 6.55 5.8 …
②该蔬菜供给量y供给(吨)关于售价x(元/千克)的函数表达式为y供给=x-1.
③1~7月份该蔬菜售价x售价(元/千克)、成本x成本(元/千克)关于月份t的函数表达式分别为x售价=t+2,x成本=t+3,函数图象如图所示.
请解答下列问题:
(1)求a,c的值;
(2)根据所给函数图象判断哪个月出售这种蔬菜每千克获利最大,并说明理由;
(3)求该蔬菜供给量与需求量相等时的售价,以及按此价格出售获得的总利润.
16.为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某校准备在校园里利用围墙(墙长12 m)和21 m长的篱笆墙,围成Ⅰ、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案(除围墙外,实线部分为篱笆墙,且不浪费篱笆墙),请根据设计方案回答下列问题:
(1)方案一:如图①,全部利用围墙的长度,但要在Ⅰ区中留一个宽度AE=1 m的水池且需保证总种植面积为32 m2,试分别确定CG、DG的长;
(2)方案二:如图②,若围成的Ⅰ、Ⅱ两块矩形的总种植面积最大,则BC应设计为多长 此时最大面积为多少
图1 图2
17.为应对全球变暖,落实国家节能减排政策,某公司积极进行技术创新,将原本直接排放进大气中的二氧化碳转化为固态形式的化工产品,从而实现变废为宝、低碳排放.经过生产实践和数据分析,在这种技术下,该公司二氧化碳月处理成本y(万元)与二氧化碳月处理量x(2≤x≤6,单位:百吨)之间满足的二次函数关系如图所示,已知点A(2,2),顶点B(3,1.5),假设每处理一百吨二氧化碳得到的化工产品的收入为2万元.
(1)求该公司二氧化碳月处理成本y(万元)与二氧化碳月处理量x(2≤x≤6,单位:百吨)之间的函数解析式;
(2)该公司利用这种技术处理二氧化碳的最大月收益W(万元)是多少 (月收益=月收入-月处理成本)
18.第二十四届冬奥会成功举办,在跳台滑雪项目中,运动员首先沿着跳台助滑道飞速下滑,然后在起跳点腾空,身体在空中飞行至着陆坡着陆,再滑行到停止区终止.本项目主要考核运动员的飞行距离和动作姿态,某数学兴趣小组对该项目中的数学问题进行了深入研究:
如图为该兴趣小组绘制的赛道截面图,以停止区CD所在水平线为x轴,过起跳点A与x轴垂直的直线为y轴,O为坐标原点,建立平面直角坐标系.着陆坡AC的坡角为30°,OA=65 m.某运动员在A处起跳腾空后,飞行至着陆坡的B处着陆,AB=100 m.在空中飞行过程中,运动员到x轴的距离y(m)与水平方向移动的距离x(m)具备二次函数关系,其解析式为y=-x2+bx+c.
(1)求b、c的值.
(2)进一步研究发现,运动员在飞行过程中,其水平方向移动的距离x(m)与飞行时间t(s)具备一次函数关系,当运动员在起跳点腾空时,t=0,x=0;空中飞行5 s后着陆.
①求x关于t的函数解析式;
②当t为何值时,运动员离着陆坡的竖直距离h(m)最大 最大值是多少
一、选择题
1.用一条长为40 cm的绳子围成一个面积为S cm2的矩形,则S的值不可能为 ( )
A.20 B.40 C.100 D.120
2.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价金额x(元)之间满足函数关系式y=-2x2+60x+800,则获利最多为 ( )
A.15元 B.400元 C.800元 D.1 250元
3.如图,在长为20 m、宽为14 m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1 m,则花圃中的阴影部分有 ( )
A.最小面积,为247 m2 B.最小面积,为266 m2
C.最大面积,为247 m2 D.最大面积,为266 m2
4.如图,某农场拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1 m宽的门,已知现有材料可建墙体(不包括门)的总长为27 m,则能建成的饲养室的最大面积为(墙体的厚度忽略不计) ( )
A.75 m2 B. m2
5.某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售单价为25元时平均每天能售出8件,当销售单价每降低2元时,平均每天能多售出4件,为使该服装店平均每天的销售利润最大,则每件的定价应为 ( )
A.21元 B.22元 C.23元 D.24元
6.如图是一款抛物线形落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB=1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为 ( )
A.3.2米 B.0.32米 C.2.5米 D.1.6米
7.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=-x+30近似地表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线C2:y=-x2+bx+c运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米,那么当运动员滑出点A,且与小山坡C1的竖直距离为20米时,运动员运动的水平距离为 ( )
A.50米 B.米 C.米
8.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:①AB=24 m;②池底所在抛物线的解析式为y=x2-5;③池塘最深处到水面CD的距离为1.8 m;④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的.其中正确的是 ( )
A.①② B.②④ C.③④ D.①④
二、填空题
9.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中发现每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为 元.
10.如图,一个横截面为抛物线形的隧道的底部宽12米,高6米.车辆双向通行,若规定车辆必须在中心线两侧、距离道路边缘2米的范围内行驶,并保持车辆顶部与隧道有不少于米的空隙,则通过隧道车辆的高度限制应为 米.
11.北仑梅山所产的草莓柔嫩多汁,芳香味美,深受消费者喜爱.有一草莓种植大户,每天草莓的采摘量为300千克,当草莓的零售价为22元/千克时,刚好可以全部售完.经调查发现,零售价每上涨1元,每天的销量就减少30千克,而剩余的草莓可由批发商以18元/千克的价格统一收购,则当草莓零售价为
元/千克时,该种植户一天的销售收入最大.
三、解答题
12.2022年春,新型冠状病毒在多地区肆虐,为方便快捷确保安全,某医疗公司设计了核酸检测小屋,如图所示的是小屋的底面示意图.
设计要求小屋的高为2.4 m,现在有长2.4 m,宽1.2 m的板材20块,制作了内墙(门窗不计).求这个核酸检测小屋的最大占地面积.
13.2022年,疫情导致各行业实体店均面临前所未有的挑战,为了刺激消费,各商场对某些商品降价销售,其中鲜猪肉进价为每千克16元,当销售价为30元/千克时,每天能售出200千克,当售价每千克每降低2元时,平均每天可多售出40千克,当售价为多少时,每天的销售利润最大
14.三分线到篮球筐中心的水平距离为7 m,在三分线上投篮,刚好命中篮球筐中心.如图,篮球运动的路线可看成是抛物线y=-x2+bx+c的一部分.
(1)求抛物线的解析式;
(2)求这次投球的最高点的高度.(结果保留整数)
15.“八婺”菜场指导菜农生产和销售某种蔬菜,提供如下信息:
①统计售价与需求量的数据,发现该蔬菜需求量y需求(吨)关于售价x(元/千克)的函数图象可以看成抛物线,其表达式为y需求=ax2+c,部分对应值如下表:
售价x (元/千克) … 2.5 3 3.5 4 …
需求量 y需求(吨) … 7.75 7.2 6.55 5.8 …
②该蔬菜供给量y供给(吨)关于售价x(元/千克)的函数表达式为y供给=x-1.
③1~7月份该蔬菜售价x售价(元/千克)、成本x成本(元/千克)关于月份t的函数表达式分别为x售价=t+2,x成本=t+3,函数图象如图所示.
请解答下列问题:
(1)求a,c的值;
(2)根据所给函数图象判断哪个月出售这种蔬菜每千克获利最大,并说明理由;
(3)求该蔬菜供给量与需求量相等时的售价,以及按此价格出售获得的总利润.
16.为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某校准备在校园里利用围墙(墙长12 m)和21 m长的篱笆墙,围成Ⅰ、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案(除围墙外,实线部分为篱笆墙,且不浪费篱笆墙),请根据设计方案回答下列问题:
(1)方案一:如图①,全部利用围墙的长度,但要在Ⅰ区中留一个宽度AE=1 m的水池且需保证总种植面积为32 m2,试分别确定CG、DG的长;
(2)方案二:如图②,若围成的Ⅰ、Ⅱ两块矩形的总种植面积最大,则BC应设计为多长 此时最大面积为多少
图1 图2
17.为应对全球变暖,落实国家节能减排政策,某公司积极进行技术创新,将原本直接排放进大气中的二氧化碳转化为固态形式的化工产品,从而实现变废为宝、低碳排放.经过生产实践和数据分析,在这种技术下,该公司二氧化碳月处理成本y(万元)与二氧化碳月处理量x(2≤x≤6,单位:百吨)之间满足的二次函数关系如图所示,已知点A(2,2),顶点B(3,1.5),假设每处理一百吨二氧化碳得到的化工产品的收入为2万元.
(1)求该公司二氧化碳月处理成本y(万元)与二氧化碳月处理量x(2≤x≤6,单位:百吨)之间的函数解析式;
(2)该公司利用这种技术处理二氧化碳的最大月收益W(万元)是多少 (月收益=月收入-月处理成本)
18.第二十四届冬奥会成功举办,在跳台滑雪项目中,运动员首先沿着跳台助滑道飞速下滑,然后在起跳点腾空,身体在空中飞行至着陆坡着陆,再滑行到停止区终止.本项目主要考核运动员的飞行距离和动作姿态,某数学兴趣小组对该项目中的数学问题进行了深入研究:
如图为该兴趣小组绘制的赛道截面图,以停止区CD所在水平线为x轴,过起跳点A与x轴垂直的直线为y轴,O为坐标原点,建立平面直角坐标系.着陆坡AC的坡角为30°,OA=65 m.某运动员在A处起跳腾空后,飞行至着陆坡的B处着陆,AB=100 m.在空中飞行过程中,运动员到x轴的距离y(m)与水平方向移动的距离x(m)具备二次函数关系,其解析式为y=-x2+bx+c.
(1)求b、c的值.
(2)进一步研究发现,运动员在飞行过程中,其水平方向移动的距离x(m)与飞行时间t(s)具备一次函数关系,当运动员在起跳点腾空时,t=0,x=0;空中飞行5 s后着陆.
①求x关于t的函数解析式;
②当t为何值时,运动员离着陆坡的竖直距离h(m)最大 最大值是多少
