2022-2023学年人教版数学七年级下册5.3.1平行线的性质(解答题)(无答案)
文档属性
| 名称 | 2022-2023学年人教版数学七年级下册5.3.1平行线的性质(解答题)(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 117.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览


文档简介
2022-2023学年5.3.1平行线的性质(解答题)
姓名: 得分: 日期:
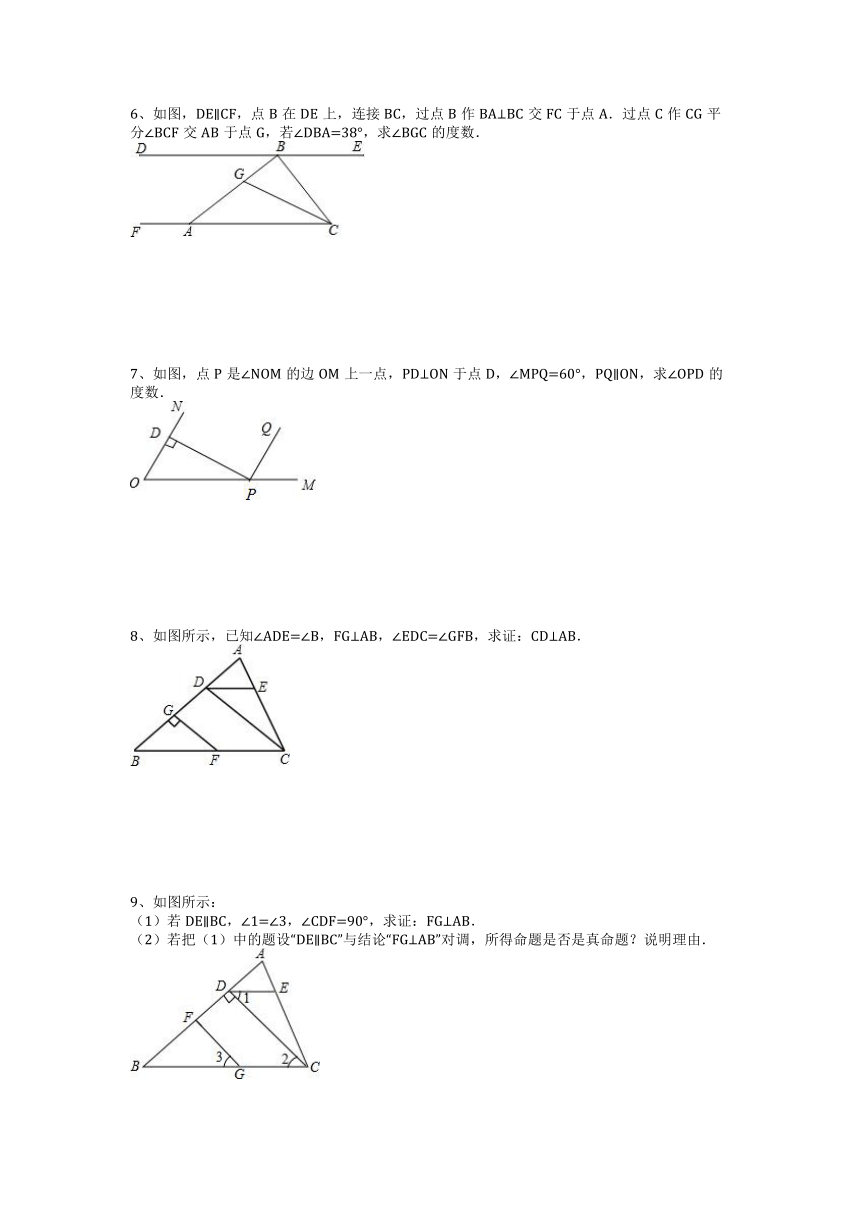
1、如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE=______度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE=______;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,∠1=45°,∠2=58°,求图中∠3与∠4的度数.
3、(1)如图1,已知AB∥CD,求证:∠EGF=∠AEG+∠CFG.
(2)如图2,已知AB∥CD,∠AEF与∠CFE的平分线交于点G.猜想∠G的度数,并证明你的猜想.
(3)如图3,已知AB∥CD,EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,∠G=95°,求∠H的度数.
4.如图,点E在直线DF上,点B在直线AC上,若∠1=∠2、∠C=∠D,试判断∠A与∠F的关系,并说明理由.
5、如图,某工程队从点A出发,沿北偏西67°方向铺设管道AD,由于某些原因,BD段不适宜铺设,需改变方向,由B点沿北偏东23°的方向继续铺设BC段,到达C点又改变方向,从C点继续铺设CE段,∠ECB应为多少度,可使所铺管道CE∥AB?试说明理由.此时CE与BC有怎样的位置关系?
6、如图,DE∥CF,点B在DE上,连接BC,过点B作BA⊥BC交FC于点A.过点C作CG平分∠BCF交AB于点G,若∠DBA=38°,求∠BGC的度数.
7、如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠MPQ=60°,PQ∥ON,求∠OPD的度数.
8、如图所示,已知∠ADE=∠B,FG⊥AB,∠EDC=∠GFB,求证:CD⊥AB.
9、如图所示:
(1)若DE∥BC,∠1=∠3,∠CDF=90°,求证:FG⊥AB.
(2)若把(1)中的题设“DE∥BC”与结论“FG⊥AB”对调,所得命题是否是真命题?说明理由.
10、如图,已知AF分别与BD、CE交于点G、H,∠1=52°,∠2=128°.
(1)求证:BD∥CE;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
11、(1)完成下面的证明.
如图,在四边形AECD中,∠1=∠2,AC是∠DAB的平分线.求证:DC∥AB.
证明:∵AC是∠DAB的平分线(已知)
∴∠______=∠______(角平分线的定义)
又∠1=∠2(已知
∴∠______=∠______(等量代换)
∴DC∥AB(______)
(2)已知线段AB=12cm,C是AB的中点,D在直线AB上,且BD= AC,画图并计算CD的长.
12、如图,已知AB∥CD,直线MN分别交AB、CD于点M、N,NG平分∠MND交AB于点G,若∠1=30°,求∠2的度数.
13、如图,已知,CD∥EF,∠1=∠2,若∠3=40°,求∠ACB的度数.
14、完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴______(同角的补角相等)①
∴______(内错角相等,两直线平行)②
∴∠ADE=∠3(______)③
∵∠3=∠B(______)④
∴______(等量代换)⑤
∴DE∥BC(______)⑥
∴∠AED=∠C(______)⑦
15、如图,已知∠1=∠2,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
16、如图,已知AE∥BF,∠A=60°,点P为射线AE上任意一点(不与点A重合),BC,BD分别平分∠ABP和∠PBF,交射线AE于点C,点D.
(1)图中∠CBD=______°;
(2)当∠ACB=∠ABD时,∠ABC=______°;
(3)随点P位置的变化,图中∠APB与∠ADB之间的数量关系始终为______,请说明理由.
17、如图①是大众汽车的图标,图②是该图标抽象的几何图形,且AC∥BD,∠A=∠B,试猜想AE与BF的位置关系,并说明理由.
18、如图1,ND∥MB,点C为ND、MB之间一点,连接CD、CB,DA平分∠NDC交MB于点A,BE平分∠MBC交ND于点E,AD与BE交于点F,∠FDC+∠ABC=180°.
(1)求证:AD∥BC;
(2)如图2,连接CF并延长至点K,若∠KFA=∠CDF,请直接写出图中所有与∠ABC相等的角.
姓名: 得分: 日期:
1、如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE=______度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE=______;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,∠1=45°,∠2=58°,求图中∠3与∠4的度数.
3、(1)如图1,已知AB∥CD,求证:∠EGF=∠AEG+∠CFG.
(2)如图2,已知AB∥CD,∠AEF与∠CFE的平分线交于点G.猜想∠G的度数,并证明你的猜想.
(3)如图3,已知AB∥CD,EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,∠G=95°,求∠H的度数.
4.如图,点E在直线DF上,点B在直线AC上,若∠1=∠2、∠C=∠D,试判断∠A与∠F的关系,并说明理由.
5、如图,某工程队从点A出发,沿北偏西67°方向铺设管道AD,由于某些原因,BD段不适宜铺设,需改变方向,由B点沿北偏东23°的方向继续铺设BC段,到达C点又改变方向,从C点继续铺设CE段,∠ECB应为多少度,可使所铺管道CE∥AB?试说明理由.此时CE与BC有怎样的位置关系?
6、如图,DE∥CF,点B在DE上,连接BC,过点B作BA⊥BC交FC于点A.过点C作CG平分∠BCF交AB于点G,若∠DBA=38°,求∠BGC的度数.
7、如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠MPQ=60°,PQ∥ON,求∠OPD的度数.
8、如图所示,已知∠ADE=∠B,FG⊥AB,∠EDC=∠GFB,求证:CD⊥AB.
9、如图所示:
(1)若DE∥BC,∠1=∠3,∠CDF=90°,求证:FG⊥AB.
(2)若把(1)中的题设“DE∥BC”与结论“FG⊥AB”对调,所得命题是否是真命题?说明理由.
10、如图,已知AF分别与BD、CE交于点G、H,∠1=52°,∠2=128°.
(1)求证:BD∥CE;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
11、(1)完成下面的证明.
如图,在四边形AECD中,∠1=∠2,AC是∠DAB的平分线.求证:DC∥AB.
证明:∵AC是∠DAB的平分线(已知)
∴∠______=∠______(角平分线的定义)
又∠1=∠2(已知
∴∠______=∠______(等量代换)
∴DC∥AB(______)
(2)已知线段AB=12cm,C是AB的中点,D在直线AB上,且BD= AC,画图并计算CD的长.
12、如图,已知AB∥CD,直线MN分别交AB、CD于点M、N,NG平分∠MND交AB于点G,若∠1=30°,求∠2的度数.
13、如图,已知,CD∥EF,∠1=∠2,若∠3=40°,求∠ACB的度数.
14、完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴______(同角的补角相等)①
∴______(内错角相等,两直线平行)②
∴∠ADE=∠3(______)③
∵∠3=∠B(______)④
∴______(等量代换)⑤
∴DE∥BC(______)⑥
∴∠AED=∠C(______)⑦
15、如图,已知∠1=∠2,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
16、如图,已知AE∥BF,∠A=60°,点P为射线AE上任意一点(不与点A重合),BC,BD分别平分∠ABP和∠PBF,交射线AE于点C,点D.
(1)图中∠CBD=______°;
(2)当∠ACB=∠ABD时,∠ABC=______°;
(3)随点P位置的变化,图中∠APB与∠ADB之间的数量关系始终为______,请说明理由.
17、如图①是大众汽车的图标,图②是该图标抽象的几何图形,且AC∥BD,∠A=∠B,试猜想AE与BF的位置关系,并说明理由.
18、如图1,ND∥MB,点C为ND、MB之间一点,连接CD、CB,DA平分∠NDC交MB于点A,BE平分∠MBC交ND于点E,AD与BE交于点F,∠FDC+∠ABC=180°.
(1)求证:AD∥BC;
(2)如图2,连接CF并延长至点K,若∠KFA=∠CDF,请直接写出图中所有与∠ABC相等的角.
