冀教版九年级下35.5 《圆与圆的位置关系》课件
文档属性
| 名称 | 冀教版九年级下35.5 《圆与圆的位置关系》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 226.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-26 20:30:12 | ||
图片预览









文档简介
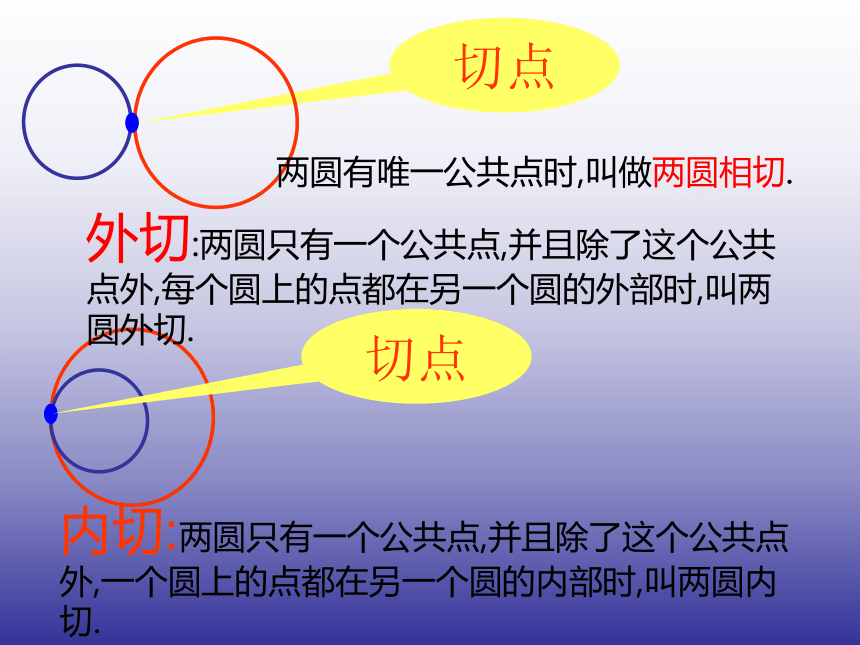
课件33张PPT。 圆与圆的位置关系护迟中学 刘立群新 北 京 新 奥 运 2 0 0 8探究活动(一)你发现两圆有那些位置关系?切点两圆有唯一公共点时,叫做两圆相切.内切:两圆只有一个公共点,并且除了这个公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切. 外切:两圆只有一个公共点,并且除了这个公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.
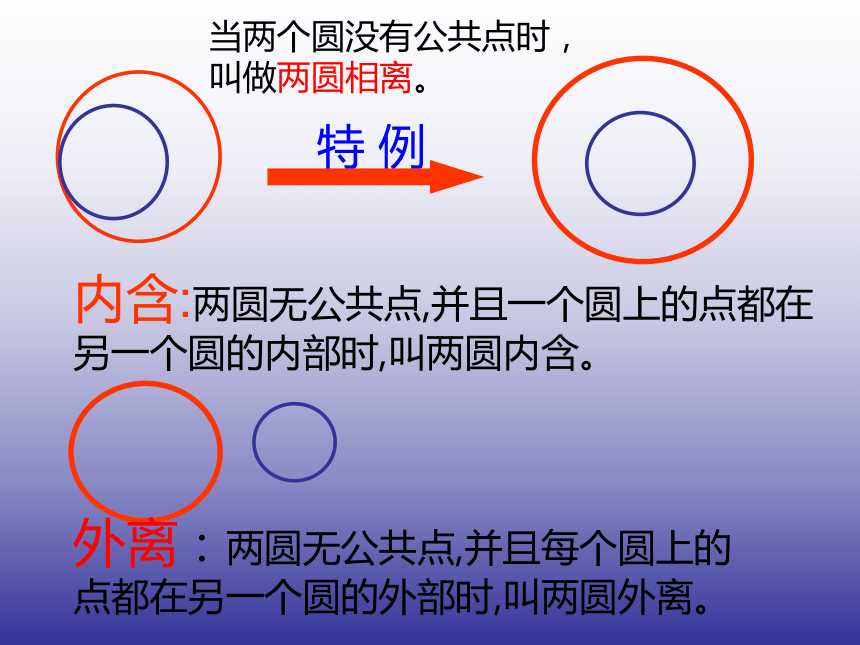
切点内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含。外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离。
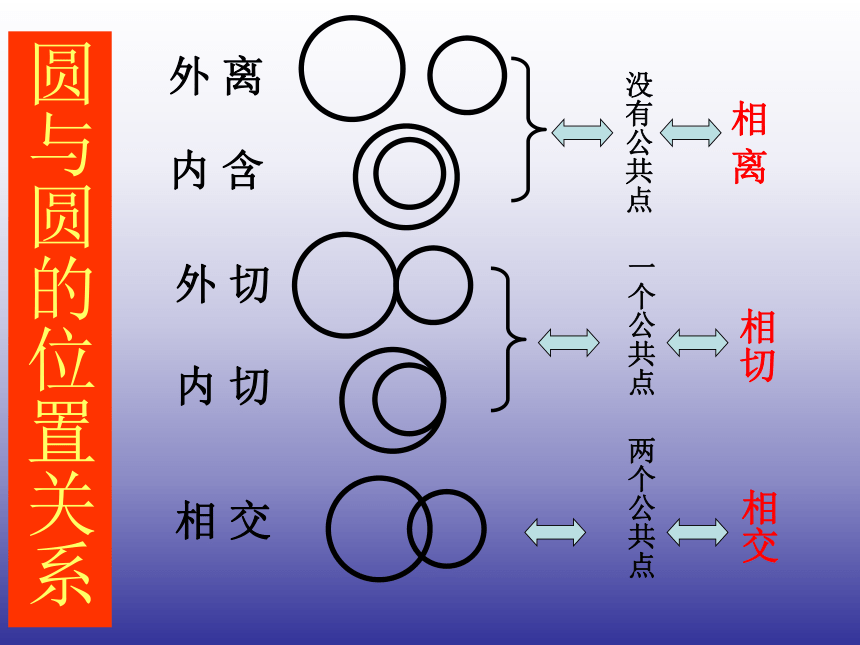
当两个圆没有公共点时,叫做两圆相离。相交:当两个圆有两个公共点时,叫两圆相交。圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交圆与圆的位置关系在你的生活中,还有哪些这样的例子?说出来,与大家分享。想一想四、相切两圆连心线性质结论:如果两圆相切,那么切点一定在连心线上.看一看圆心距:两圆心之间的距离探究活动(二)用R与r分别表示两圆的半径(R≥r),d表示圆心距。探究两圆五种位置关系时的数量关系,即d,R+r,R-r的关系。Rrdo1o2d=R+rTo1o2rRdd=R-r (R>r)To1o2Rrdd>R+ro1o2dRrR-rr)圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含圆与圆的位置关系d=R+ rd=R-r
(R>r)R- r< d<R+ r
(R>r)d>R+ rd<R- r
(R>r)填写表格(其中R、r表示两圆的半径,d表示圆心距)d>110≤d<1相交内含86练一练 1、⊙O1和⊙O2的半径分别为3cm和4cm,设:
(1)O1O2=8cm (2)O1O2=7cm (3)O1O2=5cm (4)O1O2=1cm (5)O1O2=0.5cm
(6)O1和 O2重合,⊙O1和⊙O2的位置关系怎样?练一练 2、⊙O1的⊙O2的半径分别为2cm和5cm,在下列情况下,分别求出两 圆的圆心距d的取值范围:
(1)外离 (2)外切 (3)相交
(4)内切 (5)内含练一练已知⊙O1和⊙ O2相切, ⊙ O1的半径为3厘米,圆心距d=8,则⊙ O2的半径为多少?
当外切时,R=5厘米当内切时,R=11厘米?试一试 某数学学习小组为了测量公园里放置于平台上的一个巨型球体石料的半径,采用了如下的方法:在球体石料的一侧紧挨一个已知直径的钢球,其截面如图所示,设⊙C与大圆外切的切点为D ,⊙C与大圆都与平台相切,切点为A、B且⊙C的直径为10cm,测得AB=50cm, 求球体石料的半径R。 拓展延伸小结本节课你学到了哪些知识? 设两个圆的半径为R和r ,圆心距为d,则可得
两圆外切d=R+ r
两圆内切d=R-r(R>r)
两圆相交 R- r< d<R+ r(R>r)
两圆外离d>R+ r
两圆内含d<R- r(R>r) 小结1、阅读课本。
2、做51页“习题”。
3、和圆O1(半径为2)圆O2(半径为1)都相切且半径为3的圆共有几个? 作业结束寄语 生活是数学的源泉.
探索是数学的生命线.
再见
切点内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含。外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离。
当两个圆没有公共点时,叫做两圆相离。相交:当两个圆有两个公共点时,叫两圆相交。圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交圆与圆的位置关系在你的生活中,还有哪些这样的例子?说出来,与大家分享。想一想四、相切两圆连心线性质结论:如果两圆相切,那么切点一定在连心线上.看一看圆心距:两圆心之间的距离探究活动(二)用R与r分别表示两圆的半径(R≥r),d表示圆心距。探究两圆五种位置关系时的数量关系,即d,R+r,R-r的关系。Rrdo1o2d=R+rTo1o2rRdd=R-r (R>r)To1o2Rrdd>R+ro1o2dRrR-r
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含圆与圆的位置关系d=R+ rd=R-r
(R>r)R- r< d<R+ r
(R>r)d>R+ rd<R- r
(R>r)填写表格(其中R、r表示两圆的半径,d表示圆心距)d>110≤d<1相交内含86练一练 1、⊙O1和⊙O2的半径分别为3cm和4cm,设:
(1)O1O2=8cm (2)O1O2=7cm (3)O1O2=5cm (4)O1O2=1cm (5)O1O2=0.5cm
(6)O1和 O2重合,⊙O1和⊙O2的位置关系怎样?练一练 2、⊙O1的⊙O2的半径分别为2cm和5cm,在下列情况下,分别求出两 圆的圆心距d的取值范围:
(1)外离 (2)外切 (3)相交
(4)内切 (5)内含练一练已知⊙O1和⊙ O2相切, ⊙ O1的半径为3厘米,圆心距d=8,则⊙ O2的半径为多少?
当外切时,R=5厘米当内切时,R=11厘米?试一试 某数学学习小组为了测量公园里放置于平台上的一个巨型球体石料的半径,采用了如下的方法:在球体石料的一侧紧挨一个已知直径的钢球,其截面如图所示,设⊙C与大圆外切的切点为D ,⊙C与大圆都与平台相切,切点为A、B且⊙C的直径为10cm,测得AB=50cm, 求球体石料的半径R。 拓展延伸小结本节课你学到了哪些知识? 设两个圆的半径为R和r ,圆心距为d,则可得
两圆外切d=R+ r
两圆内切d=R-r(R>r)
两圆相交 R- r< d<R+ r(R>r)
两圆外离d>R+ r
两圆内含d<R- r(R>r) 小结1、阅读课本。
2、做51页“习题”。
3、和圆O1(半径为2)圆O2(半径为1)都相切且半径为3的圆共有几个? 作业结束寄语 生活是数学的源泉.
探索是数学的生命线.
再见
