17.3.2 一次函数的图象 教案
图片预览


文档简介
中小学教育资源及组卷应用平台
17.3.2 一次函数的图象 教学设计
课题 17.3.2 一次函数的图象 单元 第17 单元 学科 数学 年级 八年级(下)
教材分析 理解函数图象的概念.经历一次函数的作图过程,初步了解作函数图象的一般步骤.会画一次函数与正比例函数的图象,并能利用一次函数的图象解决实际问题.
核心素养分析 学生在探究合作中交流体验知识的形成过程,经历一次函数的作图过程,探索某些一次函数图象的异同点;体会用类比的思想研究一次函数,体验研究数学问题的常用方法.
学习目标 1、理解一次函数和正比例函数的图象是一条直线.2、能熟练地作出一次函数和正比例函数的图象.3、会求一次函数与坐标轴的交点坐标.4、会作出实际问题中的一次函数的图象.
重点 画一次函数与正比例函数的图象,并能利用一次函数的图象解决实际问题.
难点 利用一次函数的图象解决实际问题.
教学过程
教学环节 教师活动 学生活动 设计意图
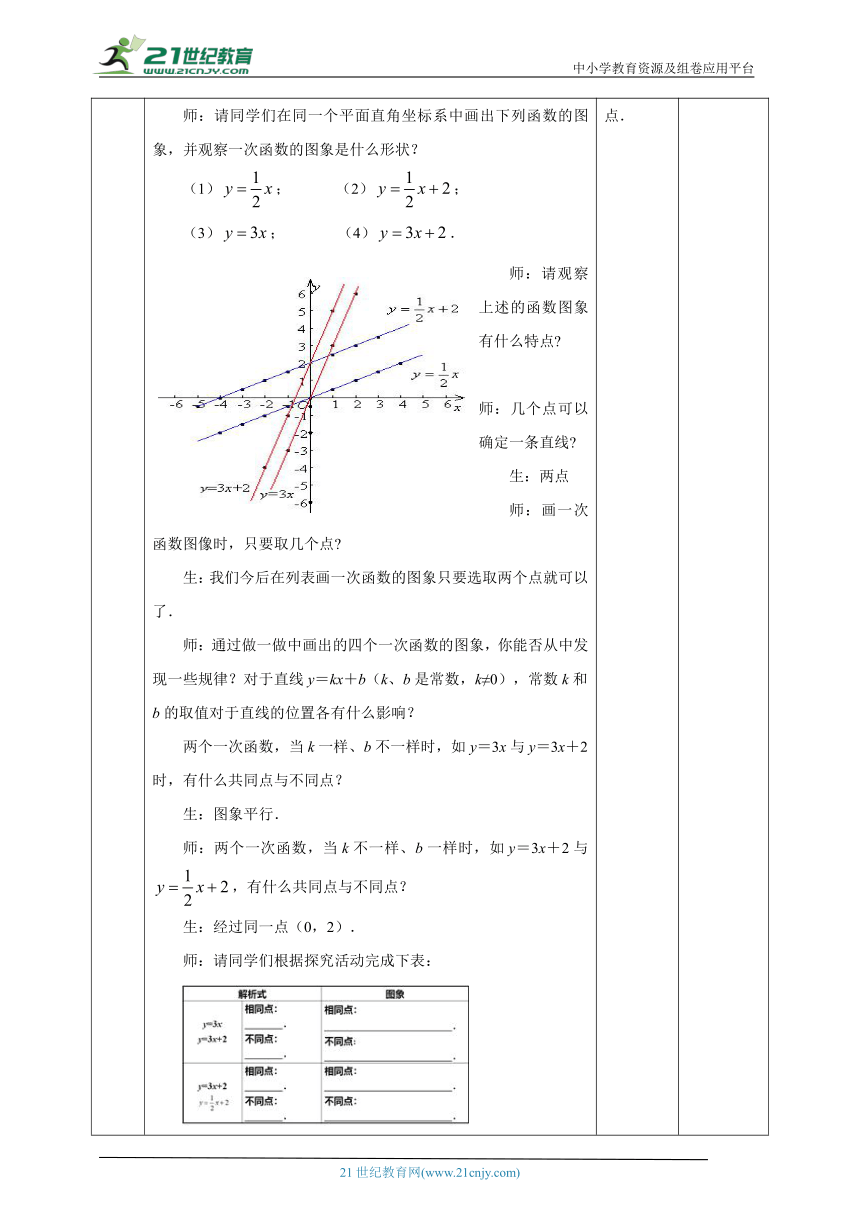
导入新课 一、创设情景,引出课题师:一次函数的概念是什么?生:一般地,形如y=kx+b(k、b是常数,k≠0)的函数,叫做一次函数.师:什么叫做正比例函数?生:特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.师:2、在未知函数图象的具体形状的情况下,怎样画出一个给定的函数图象?画函数图象的一般步骤是什么?生:用“描点法“画函数图象,可以分成(1)列表,(2)描点,(3)连线.师:同学们知识一次函数的图象是什么形状?上节课我们主要学习了一次函数、正比例函数的概念,本节课我们就来探究一次函数与正比例函数的图象.一次函数和正比例函数的图象:师:请同学们在同一个平面直角坐标系中画出下列函数的图象,并观察一次函数的图象是什么形状?(1); (2);(3); (4).师:请观察上述的函数图象有什么特点 师:几个点可以确定一条直线 生:两点师:画一次函数图像时,只要取几个点 生:我们今后在列表画一次函数的图象只要选取两个点就可以了.师:通过做一做中画出的四个一次函数的图象,你能否从中发现一些规律?对于直线y=kx+b(k、b是常数,k≠0),常数k和b的取值对于直线的位置各有什么影响?两个一次函数,当k一样、b不一样时,如y=3x与y=3x+2时,有什么共同点与不同点?生:图象平行.师:两个一次函数,当k不一样、b一样时,如y=3x+2与,有什么共同点与不同点?生:经过同一点(0,2).师:请同学们根据探究活动完成下表:归纳总结:根据以上的分析,我们可以得出结论:在直线y=k1x+b1与直线y=k2x+b2中,如果k1= k2 ,那么这两条直线平行.如果b1 = b2 ,那么这两条直线与y轴相交于同一个点.如果b=0,那么(正比例)函数y=kx的图象一定经过点(0,0),即原点.解析式中的k决定两条直线是否平行,而b决定与y轴的交点位置.函数图象的平移:观察函数y=3x和y=3x+2的图象,我们知道:它们是互相平行的,所以,其中 一条直线可以看作是由另一条直线平移得到的.师:你能说出直线y=3x+2是由直线y=3x怎样平移得到的吗?生:直线y=3x+2是由直线y=3x向上平移2个单位得到的.归纳总结:(1)当b>0时,向上平移;y=2x上移2个单位得到y=2x+2. 2)当b<0时,向下平移;y=x下移3个单位得到y=x-3. 思考自议21通过画函数图象培养学生动手操作的能力,归纳一次函数的图象是一条直线,特别正比例函数图象经过原点. 纪教 通过对问题的探究使学生理妥k和b的取值对图象的位置的影响,让学生直观体会直线 y=kx+b中k和b的几何意义.
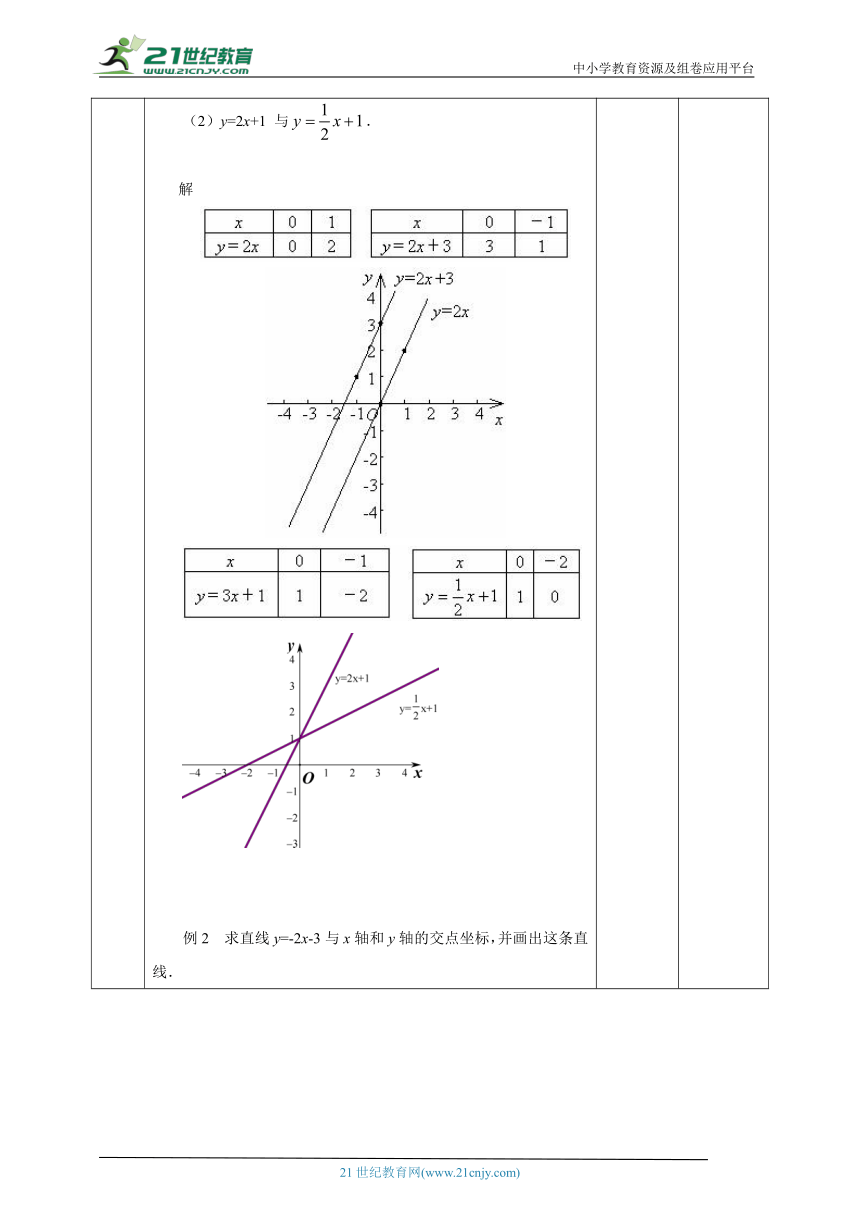
讲授新课 二、提炼概念概括:一次函数()的图象时一条 ,正比例函数的图象是经过 的一条直线,若两直线值相同,则这两直线互相 ,直线看作是由平移 单位得到的,时,向 平移,时,向 平移;向右平移()个单位得到 ,向左平移()个单位得到 .三、典例精讲例1 在同一个平面直角坐标系中画出下列函数的图像:(1)y=2x与 y=2x+3;(2)y=2x+1 与.解 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )例2 求直线y=-2x-3与x轴和y轴的交点坐标,并画出这条直线.师:请同学们讨论这里是取哪两个特殊点来做直线的?这样做有什么好处?例3 问题1中,汽车距北京的距离s千米,与汽车在高速公路上行驶的时间t时之间的函数关系式是s=570-95t,试画出这个函数图象.画出这个函数图象并讨论:这里自变量t的取值范围是什么?函数的图象是什么样的图形?解:0≤t≤6, 函数的图象是直线的一部分(一条线段).具体问题要考虑实际情况利用一次函数的图象解决实际问题. 通过观察函数图象,归纳函数图象平移的特点. 21世纪观察函数的图象,归纳函数图象的平移,掌握一次函数图象的平移.
课堂练习 四、巩固训练1.在下列图象中,能作为一次函数y=-x+1的图象的是( )A2.将直线y=2x-3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为 ( )A.y=2x-4 B.y=2x+4 C.y=2x+2 D.y=2x-2A3、函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),则k= ,b= .-2,34.请大家在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.5.已知一次函数y=-1/2x+2的图象与x轴、y轴分别交于A,B 两点.(1)求A,B 两点的坐标;(2)求直线与两坐标轴围成的三角形的面积.解:(1)在一次函数y=-1/2x+2中,令y=0,则x=4令x=0,则y=2∴A(4,0),B(0,2)(2)由A(4,0),B(0,2)可得AO=4,BO=2∴S_ AOB=1/2AO×BO=4
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
17.3.2 一次函数的图象 教学设计
课题 17.3.2 一次函数的图象 单元 第17 单元 学科 数学 年级 八年级(下)
教材分析 理解函数图象的概念.经历一次函数的作图过程,初步了解作函数图象的一般步骤.会画一次函数与正比例函数的图象,并能利用一次函数的图象解决实际问题.
核心素养分析 学生在探究合作中交流体验知识的形成过程,经历一次函数的作图过程,探索某些一次函数图象的异同点;体会用类比的思想研究一次函数,体验研究数学问题的常用方法.
学习目标 1、理解一次函数和正比例函数的图象是一条直线.2、能熟练地作出一次函数和正比例函数的图象.3、会求一次函数与坐标轴的交点坐标.4、会作出实际问题中的一次函数的图象.
重点 画一次函数与正比例函数的图象,并能利用一次函数的图象解决实际问题.
难点 利用一次函数的图象解决实际问题.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题师:一次函数的概念是什么?生:一般地,形如y=kx+b(k、b是常数,k≠0)的函数,叫做一次函数.师:什么叫做正比例函数?生:特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.师:2、在未知函数图象的具体形状的情况下,怎样画出一个给定的函数图象?画函数图象的一般步骤是什么?生:用“描点法“画函数图象,可以分成(1)列表,(2)描点,(3)连线.师:同学们知识一次函数的图象是什么形状?上节课我们主要学习了一次函数、正比例函数的概念,本节课我们就来探究一次函数与正比例函数的图象.一次函数和正比例函数的图象:师:请同学们在同一个平面直角坐标系中画出下列函数的图象,并观察一次函数的图象是什么形状?(1); (2);(3); (4).师:请观察上述的函数图象有什么特点 师:几个点可以确定一条直线 生:两点师:画一次函数图像时,只要取几个点 生:我们今后在列表画一次函数的图象只要选取两个点就可以了.师:通过做一做中画出的四个一次函数的图象,你能否从中发现一些规律?对于直线y=kx+b(k、b是常数,k≠0),常数k和b的取值对于直线的位置各有什么影响?两个一次函数,当k一样、b不一样时,如y=3x与y=3x+2时,有什么共同点与不同点?生:图象平行.师:两个一次函数,当k不一样、b一样时,如y=3x+2与,有什么共同点与不同点?生:经过同一点(0,2).师:请同学们根据探究活动完成下表:归纳总结:根据以上的分析,我们可以得出结论:在直线y=k1x+b1与直线y=k2x+b2中,如果k1= k2 ,那么这两条直线平行.如果b1 = b2 ,那么这两条直线与y轴相交于同一个点.如果b=0,那么(正比例)函数y=kx的图象一定经过点(0,0),即原点.解析式中的k决定两条直线是否平行,而b决定与y轴的交点位置.函数图象的平移:观察函数y=3x和y=3x+2的图象,我们知道:它们是互相平行的,所以,其中 一条直线可以看作是由另一条直线平移得到的.师:你能说出直线y=3x+2是由直线y=3x怎样平移得到的吗?生:直线y=3x+2是由直线y=3x向上平移2个单位得到的.归纳总结:(1)当b>0时,向上平移;y=2x上移2个单位得到y=2x+2. 2)当b<0时,向下平移;y=x下移3个单位得到y=x-3. 思考自议21通过画函数图象培养学生动手操作的能力,归纳一次函数的图象是一条直线,特别正比例函数图象经过原点. 纪教 通过对问题的探究使学生理妥k和b的取值对图象的位置的影响,让学生直观体会直线 y=kx+b中k和b的几何意义.
讲授新课 二、提炼概念概括:一次函数()的图象时一条 ,正比例函数的图象是经过 的一条直线,若两直线值相同,则这两直线互相 ,直线看作是由平移 单位得到的,时,向 平移,时,向 平移;向右平移()个单位得到 ,向左平移()个单位得到 .三、典例精讲例1 在同一个平面直角坐标系中画出下列函数的图像:(1)y=2x与 y=2x+3;(2)y=2x+1 与.解 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )例2 求直线y=-2x-3与x轴和y轴的交点坐标,并画出这条直线.师:请同学们讨论这里是取哪两个特殊点来做直线的?这样做有什么好处?例3 问题1中,汽车距北京的距离s千米,与汽车在高速公路上行驶的时间t时之间的函数关系式是s=570-95t,试画出这个函数图象.画出这个函数图象并讨论:这里自变量t的取值范围是什么?函数的图象是什么样的图形?解:0≤t≤6, 函数的图象是直线的一部分(一条线段).具体问题要考虑实际情况利用一次函数的图象解决实际问题. 通过观察函数图象,归纳函数图象平移的特点. 21世纪观察函数的图象,归纳函数图象的平移,掌握一次函数图象的平移.
课堂练习 四、巩固训练1.在下列图象中,能作为一次函数y=-x+1的图象的是( )A2.将直线y=2x-3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为 ( )A.y=2x-4 B.y=2x+4 C.y=2x+2 D.y=2x-2A3、函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),则k= ,b= .-2,34.请大家在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.5.已知一次函数y=-1/2x+2的图象与x轴、y轴分别交于A,B 两点.(1)求A,B 两点的坐标;(2)求直线与两坐标轴围成的三角形的面积.解:(1)在一次函数y=-1/2x+2中,令y=0,则x=4令x=0,则y=2∴A(4,0),B(0,2)(2)由A(4,0),B(0,2)可得AO=4,BO=2∴S_ AOB=1/2AO×BO=4
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
