17.3.2 一次函数的图象 课件(共24张PPT)
文档属性
| 名称 | 17.3.2 一次函数的图象 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 08:08:43 | ||
图片预览







文档简介
(共24张PPT)
17.3.2 一次函数的图象
华师大版 八年级 下册
教学目标
教学目标:1.会利用描点法画一次函数的图象;通过观察归纳出两点法
画一次函数图象.
2.通过一次函数图象总结出图象平移规律并应用解题.
教学重点:画一次函数与正比例函数的图象,并能利用一次函数的图象
解决实际问题.
教学难点:利用一次函数的图象解决实际问题.
新知导入
情境引入
1、画函数图象的一般步骤:
(1)列表
(2)描点
(3)连线
2、一次函数的概念
解析式都是自变量的一次整式.
表示:y=kx+b (k.b是常量,k≠0)
注意:x的次数=1,kx+b是整式.
当b=0时,一次函数y=kx(常数k≠0 )叫正比例函数.
一次函数的图象是什么形状呢?
做一做
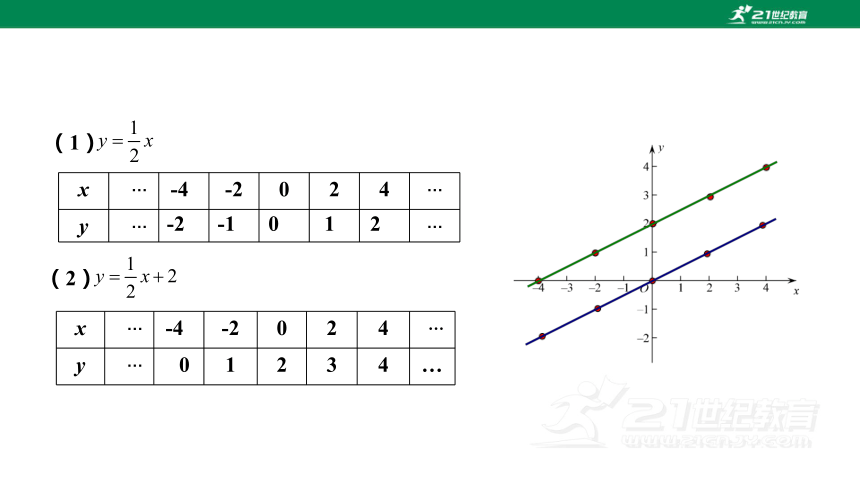
在同一个平面直角坐标系中画出下列函数的图象.
y=x (2) y=x+2
(3) y=3x (4) y=3x+2
观察:一次函数的图象是什么形状?
x … -4 -2 0 2 4 …
y … 0 1 2 3 4 …
x … -4 -2 0 2 4 …
y … …
-2
2
1
0
-1
(1)
(2)
(3)
x … -1 0 1 …
y … -3 0 3 …
(4)
x … -1 0 1 …
y … -1 2 5 …
新知讲解
合作学习
观察函数的解析式及其图象,填写下表。
y=3x
y=3x+2
解析式 图象
y=3x y=3x+2 相同点:________。 不同点: ________。 相同点:________________________
不同点:
_________________
相同点:________。 不同点: ________。 相同点:________________________
不同点:___________________
y=3x+2 相同点:________。 不同点: ________。 相同点:________________________
不同点:__________________
k相同
b不同
k相同
b不同
(平行,一条平移可得另一条)
直线y=3x+2还经过第二象限
(平行一条平移可得另一条)
直线 还经过第二象限
b相同
k不同
都与y轴相交于点(0,2)
倾斜度不一样(不平行,相交)
演示平移关系
提炼概念
一次函数 y=kx+b(k≠0)的图象是一条直线.通常也称为直线y=kx+b .
特别地,正比例函数y=kx(k≠0 )的图象是经过原点(0,0)的一条直线.
值得注意的是:一次函数的图象不可能与坐标轴平行.
概括
根据以上的分析,我们可以得出结论:在直线y=k1x+b1与直线y=k2x+b2中,如果k1= k2 ,那么这两条直线平行.如果b1 = b2 ,那么这两条直线与y轴相交于同一个点.
如果b=0,那么(正比例)函数y=kx的图象一定经过点(0,0),即原点.
解析式中的k决定两条直线是否平行,而b决定与y轴的交点位置.
观察函数y=3x和y=3x+2的图象,我们知道:它们是互相平行的,所以,其中 一条直线可以看作是由另一条直线平移得到的.
你能说出直线y=3x+2是由直线y=3x怎样平移得到的吗?
直线y=3x+2是由直线y=3x向上平移2个单位得到的.
(2)当b<0时, ________.
图象的平移:
|b|个单位
向上平移
向下平移
y=2x y=2x+2
上移2个单位
y=x y=x-3
下移3个单位
y=kx
y=kx+b
向上(或向下)平移
(1)当b>0时,________;
典例精讲
例1 在同一个平面直角坐标系中画出下列函数的图像:
(1)y=2x与 y=2x+3;
(2)y=2x+1 与 .
解:列表
x 0 1
y=2x 0 2
x 0 -1
y=2x+3 3 1
x 0 1
y=2x+1 1 3
例2 求直线y= -2x-3与x轴和y轴的交点,并画出这条直线.
这里是取哪两个特殊点来做直线的?这样做有什么好处?
例3 问题1中,汽车距北京的距离s千米,与汽车在高速公路上行驶的时间t时之间的函数关系式是s=570-95t,试画出这个函数图象.
画出这个函数图象并讨论:
这里自变量t的取值范围是什么?
函数的图象是什么样的图形?
0≤t≤6,
函数的图象是直线的一部分(一条线段).具体问题要考虑实际情况利用一次函数的图象解决实际问题.
归纳概念
直线y=kx+b
(k≠0)与
坐标轴的交点
注意:|b|,| |是直线y=kx+b(k≠0)与坐标轴的两交
点和原点构成的直角三角形的两直角边的长.
与x轴的交点坐标为( ,0)
与y轴的交点坐标为(0,b)
方程kx+b=0的解是x=
归纳总结
课堂练习
1.在下列图象中,能作为一次函数y=-x+1的图象的是( )
A
2.将直线y=2x-3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为 ( )
A.y=2x-4 B.y=2x+4 C.y=2x+2 D.y=2x-2
A
3.函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),
则k= ,b= .
3
-2
x
y
2
0
.
.
.
.
4.在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.
.
.
y=-x
y=-x+2
y=-x-2
x
y=-x
x
y=-x+2
x
y=-x-2
0
-2
0
-2
0
0
1
-1
0
0
2
2
5.已知一次函数y=-x+2的图象与x轴、y轴分别交于A,B 两点.
(1)求A,B 两点的坐标;
(2)求直线与两坐标轴围成的三角形的面积.
课堂总结
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.3.2 一次函数的图象
华师大版 八年级 下册
教学目标
教学目标:1.会利用描点法画一次函数的图象;通过观察归纳出两点法
画一次函数图象.
2.通过一次函数图象总结出图象平移规律并应用解题.
教学重点:画一次函数与正比例函数的图象,并能利用一次函数的图象
解决实际问题.
教学难点:利用一次函数的图象解决实际问题.
新知导入
情境引入
1、画函数图象的一般步骤:
(1)列表
(2)描点
(3)连线
2、一次函数的概念
解析式都是自变量的一次整式.
表示:y=kx+b (k.b是常量,k≠0)
注意:x的次数=1,kx+b是整式.
当b=0时,一次函数y=kx(常数k≠0 )叫正比例函数.
一次函数的图象是什么形状呢?
做一做
在同一个平面直角坐标系中画出下列函数的图象.
y=x (2) y=x+2
(3) y=3x (4) y=3x+2
观察:一次函数的图象是什么形状?
x … -4 -2 0 2 4 …
y … 0 1 2 3 4 …
x … -4 -2 0 2 4 …
y … …
-2
2
1
0
-1
(1)
(2)
(3)
x … -1 0 1 …
y … -3 0 3 …
(4)
x … -1 0 1 …
y … -1 2 5 …
新知讲解
合作学习
观察函数的解析式及其图象,填写下表。
y=3x
y=3x+2
解析式 图象
y=3x y=3x+2 相同点:________。 不同点: ________。 相同点:________________________
不同点:
_________________
相同点:________。 不同点: ________。 相同点:________________________
不同点:___________________
y=3x+2 相同点:________。 不同点: ________。 相同点:________________________
不同点:__________________
k相同
b不同
k相同
b不同
(平行,一条平移可得另一条)
直线y=3x+2还经过第二象限
(平行一条平移可得另一条)
直线 还经过第二象限
b相同
k不同
都与y轴相交于点(0,2)
倾斜度不一样(不平行,相交)
演示平移关系
提炼概念
一次函数 y=kx+b(k≠0)的图象是一条直线.通常也称为直线y=kx+b .
特别地,正比例函数y=kx(k≠0 )的图象是经过原点(0,0)的一条直线.
值得注意的是:一次函数的图象不可能与坐标轴平行.
概括
根据以上的分析,我们可以得出结论:在直线y=k1x+b1与直线y=k2x+b2中,如果k1= k2 ,那么这两条直线平行.如果b1 = b2 ,那么这两条直线与y轴相交于同一个点.
如果b=0,那么(正比例)函数y=kx的图象一定经过点(0,0),即原点.
解析式中的k决定两条直线是否平行,而b决定与y轴的交点位置.
观察函数y=3x和y=3x+2的图象,我们知道:它们是互相平行的,所以,其中 一条直线可以看作是由另一条直线平移得到的.
你能说出直线y=3x+2是由直线y=3x怎样平移得到的吗?
直线y=3x+2是由直线y=3x向上平移2个单位得到的.
(2)当b<0时, ________.
图象的平移:
|b|个单位
向上平移
向下平移
y=2x y=2x+2
上移2个单位
y=x y=x-3
下移3个单位
y=kx
y=kx+b
向上(或向下)平移
(1)当b>0时,________;
典例精讲
例1 在同一个平面直角坐标系中画出下列函数的图像:
(1)y=2x与 y=2x+3;
(2)y=2x+1 与 .
解:列表
x 0 1
y=2x 0 2
x 0 -1
y=2x+3 3 1
x 0 1
y=2x+1 1 3
例2 求直线y= -2x-3与x轴和y轴的交点,并画出这条直线.
这里是取哪两个特殊点来做直线的?这样做有什么好处?
例3 问题1中,汽车距北京的距离s千米,与汽车在高速公路上行驶的时间t时之间的函数关系式是s=570-95t,试画出这个函数图象.
画出这个函数图象并讨论:
这里自变量t的取值范围是什么?
函数的图象是什么样的图形?
0≤t≤6,
函数的图象是直线的一部分(一条线段).具体问题要考虑实际情况利用一次函数的图象解决实际问题.
归纳概念
直线y=kx+b
(k≠0)与
坐标轴的交点
注意:|b|,| |是直线y=kx+b(k≠0)与坐标轴的两交
点和原点构成的直角三角形的两直角边的长.
与x轴的交点坐标为( ,0)
与y轴的交点坐标为(0,b)
方程kx+b=0的解是x=
归纳总结
课堂练习
1.在下列图象中,能作为一次函数y=-x+1的图象的是( )
A
2.将直线y=2x-3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为 ( )
A.y=2x-4 B.y=2x+4 C.y=2x+2 D.y=2x-2
A
3.函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),
则k= ,b= .
3
-2
x
y
2
0
.
.
.
.
4.在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.
.
.
y=-x
y=-x+2
y=-x-2
x
y=-x
x
y=-x+2
x
y=-x-2
0
-2
0
-2
0
0
1
-1
0
0
2
2
5.已知一次函数y=-x+2的图象与x轴、y轴分别交于A,B 两点.
(1)求A,B 两点的坐标;
(2)求直线与两坐标轴围成的三角形的面积.
课堂总结
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
