湖南省岳阳市岳阳县三校2022-2023学年九年级上学期期末联合测试数学试题(含答案)
文档属性
| 名称 | 湖南省岳阳市岳阳县三校2022-2023学年九年级上学期期末联合测试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 105.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 18:23:42 | ||
图片预览


文档简介
2022年上学期九年级期末联合测试
数 学
考生注意:1.本学科试卷分为试题卷和答题卡两部分;
2.请将姓名、准考证号相关信息按要求填写在答题卡上;
3.请按答题卡上的注意事项在答题卡上作答,答在试题卷上的无效;
一、单选题(共48分)
1.若函数是反比例函数,则的取值为 ( )
A. B. C.或 D.
2.一次函数与反比例函数在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
3.如图,点是反比例函数≠的图象上任意一点,过点作轴,垂足为.若的面积等于,则的值等于( )
A. B. C. D.
4.公元前世纪,古希腊科学家阿基米德发现了杠杆平衡.后来人们把它归纳为“杠杆原理”,即:阻力阻力臂=动力动力臂.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别是和,则动力(单位:关于动力臂(单位:)的函数解析式正确的是( )
A. B. C. D.
5.用配方法解一元二次方程,配方正确的是( )
A. B.
C. D.
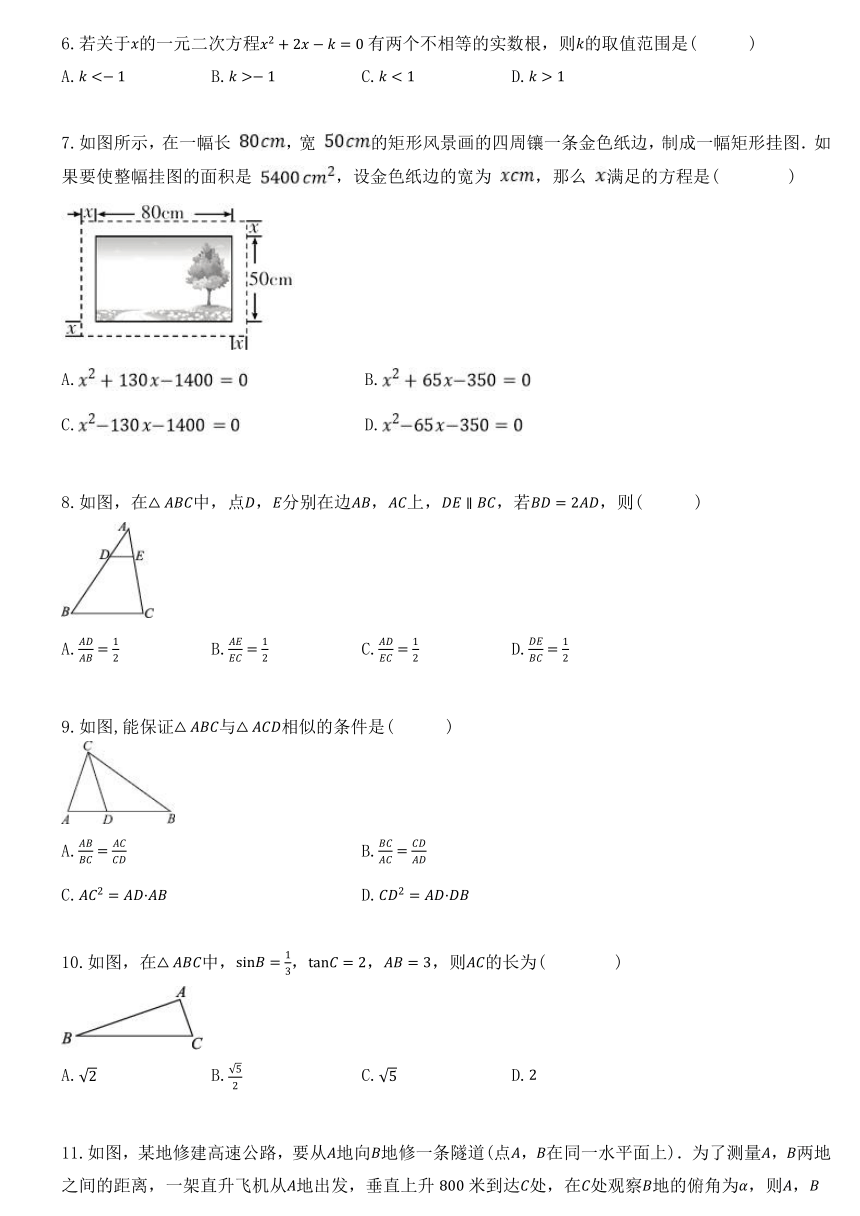
6.若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. C. D.
7.如图所示,在一幅长 ,宽 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是 ,设金色纸边的宽为 ,那么 满足的方程是( )
A. B.
C. D.
8.如图,在中,点,分别在边,上,,若,则( )
A. B. C. D.
9.如图,能保证与相似的条件是( )
A. B.
C. D.
10.如图,在中,,,,则的长为( )
A. B. C. D.
11.如图,某地修建高速公路,要从地向地修一条隧道(点,在同一水平面上).为了测量,两地之间的距离,一架直升飞机从地出发,垂直上升米到达处,在处观察地的俯角为,则,两地之间的距离为( )
A.米 B.米 C.米 D.米
12.如图,若内一点满足,则点为的布洛卡点.三角形的布洛卡点由法国数学家和数学教育家克洛尔..于年首次发现,但他的发现并未被当时的人们所注意.年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知在等腰直角三角形中,.若为的布洛卡点,,则+的值为( )
A. B. C.+ D.+
二、填空题(共20分)
13.在中,,,,那么的余弦值是 .
14.若点,,,,,都在反比例函数为常数)的图象上,则,,的大小关系为 .
15.《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为平方步,只知道它的长与宽共步,问它的长比宽多多少步?根据题意得,长比宽多 步.
16. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度如图,身高的小明从路灯灯泡的正下方点处,沿着平直的道路走到达点处,测得影子长是,则路灯灯泡离地面的高度为
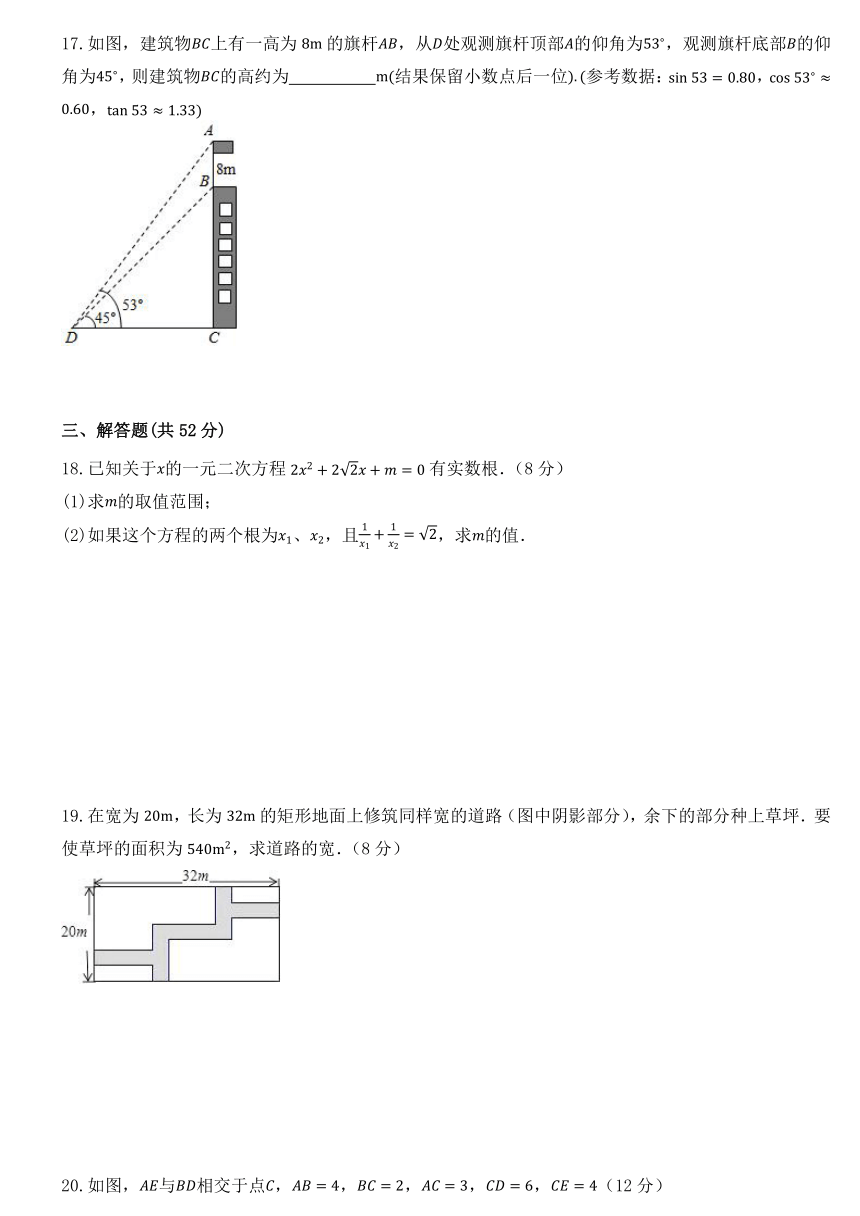
17.如图,建筑物上有一高为的旗杆,从处观测旗杆顶部的仰角为,观测旗杆底部的仰角为,则建筑物的高约为 结果保留小数点后一位参考数据:,,
三、解答题(共52分)
18.已知关于的一元二次方程有实数根.(8分)
(1)求的取值范围;
(2)如果这个方程的两个根为、,且,求的值.
19.在宽为,长为的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为,求道路的宽.(8分)
20.如图,与相交于点,,,,,(12分)
(1)与是否相似?为什么?
(2)求的长.
21.脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上点测得屋顶的仰角为,此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为,房屋的顶层横梁,,交于点(点,,在同一水平线上).(参考数据:,,, (12分)
(1)求屋顶到横梁的距离;
(2)求房屋的高(结果精确到
22.如图,已知函数,的图象与一次函数+的图象相交于不同的两点,过点作轴于点,连接,其中点的横坐标为,的面积为. (12分)
(1)求的值及时的值;
(2)记表示不超过的最大整数,例如:,,设,若 ,求的值.
参考答案
1-12 ADABA BBBCB DD
13. 14. 15.12 16. 17.24.2
18
(1)解:∵方程.有实数根,∴(),解得:;
(2)∵,,
∴由可得:,
解得:.
19.解:设道路的宽为,根据题意得:
,
解得:,(不合题意,舍去),
答:道路的宽是.
20
(1)相似.
理由:∵,,
∴.
又∵,
∴∽.
(2)∵∽,
∴,
∴.
21
(1)解:易得,,
在中,,,
,,
.
答:屋顶到横梁的距离约为.
(2)如图, 过作于,
设, 在中,,,
,
,
在中,,,
,
,
,
,
解得,
.
答:房屋的高约为.
22
(1)解:∵, ∴, ∴. ∵, ∴, ∴,. 将点的坐标代入+, 得
(2)解:由一次函数+可得点的坐标为, ∴. 将代入+, 得+, ∴+. ∵,, ∴. ∵, ∴, ∴. ∵, ∴, ∴
数 学
考生注意:1.本学科试卷分为试题卷和答题卡两部分;
2.请将姓名、准考证号相关信息按要求填写在答题卡上;
3.请按答题卡上的注意事项在答题卡上作答,答在试题卷上的无效;
一、单选题(共48分)
1.若函数是反比例函数,则的取值为 ( )
A. B. C.或 D.
2.一次函数与反比例函数在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
3.如图,点是反比例函数≠的图象上任意一点,过点作轴,垂足为.若的面积等于,则的值等于( )
A. B. C. D.
4.公元前世纪,古希腊科学家阿基米德发现了杠杆平衡.后来人们把它归纳为“杠杆原理”,即:阻力阻力臂=动力动力臂.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别是和,则动力(单位:关于动力臂(单位:)的函数解析式正确的是( )
A. B. C. D.
5.用配方法解一元二次方程,配方正确的是( )
A. B.
C. D.
6.若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. C. D.
7.如图所示,在一幅长 ,宽 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是 ,设金色纸边的宽为 ,那么 满足的方程是( )
A. B.
C. D.
8.如图,在中,点,分别在边,上,,若,则( )
A. B. C. D.
9.如图,能保证与相似的条件是( )
A. B.
C. D.
10.如图,在中,,,,则的长为( )
A. B. C. D.
11.如图,某地修建高速公路,要从地向地修一条隧道(点,在同一水平面上).为了测量,两地之间的距离,一架直升飞机从地出发,垂直上升米到达处,在处观察地的俯角为,则,两地之间的距离为( )
A.米 B.米 C.米 D.米
12.如图,若内一点满足,则点为的布洛卡点.三角形的布洛卡点由法国数学家和数学教育家克洛尔..于年首次发现,但他的发现并未被当时的人们所注意.年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知在等腰直角三角形中,.若为的布洛卡点,,则+的值为( )
A. B. C.+ D.+
二、填空题(共20分)
13.在中,,,,那么的余弦值是 .
14.若点,,,,,都在反比例函数为常数)的图象上,则,,的大小关系为 .
15.《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为平方步,只知道它的长与宽共步,问它的长比宽多多少步?根据题意得,长比宽多 步.
16. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度如图,身高的小明从路灯灯泡的正下方点处,沿着平直的道路走到达点处,测得影子长是,则路灯灯泡离地面的高度为
17.如图,建筑物上有一高为的旗杆,从处观测旗杆顶部的仰角为,观测旗杆底部的仰角为,则建筑物的高约为 结果保留小数点后一位参考数据:,,
三、解答题(共52分)
18.已知关于的一元二次方程有实数根.(8分)
(1)求的取值范围;
(2)如果这个方程的两个根为、,且,求的值.
19.在宽为,长为的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为,求道路的宽.(8分)
20.如图,与相交于点,,,,,(12分)
(1)与是否相似?为什么?
(2)求的长.
21.脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上点测得屋顶的仰角为,此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为,房屋的顶层横梁,,交于点(点,,在同一水平线上).(参考数据:,,, (12分)
(1)求屋顶到横梁的距离;
(2)求房屋的高(结果精确到
22.如图,已知函数,的图象与一次函数+的图象相交于不同的两点,过点作轴于点,连接,其中点的横坐标为,的面积为. (12分)
(1)求的值及时的值;
(2)记表示不超过的最大整数,例如:,,设,若 ,求的值.
参考答案
1-12 ADABA BBBCB DD
13. 14. 15.12 16. 17.24.2
18
(1)解:∵方程.有实数根,∴(),解得:;
(2)∵,,
∴由可得:,
解得:.
19.解:设道路的宽为,根据题意得:
,
解得:,(不合题意,舍去),
答:道路的宽是.
20
(1)相似.
理由:∵,,
∴.
又∵,
∴∽.
(2)∵∽,
∴,
∴.
21
(1)解:易得,,
在中,,,
,,
.
答:屋顶到横梁的距离约为.
(2)如图, 过作于,
设, 在中,,,
,
,
在中,,,
,
,
,
,
解得,
.
答:房屋的高约为.
22
(1)解:∵, ∴, ∴. ∵, ∴, ∴,. 将点的坐标代入+, 得
(2)解:由一次函数+可得点的坐标为, ∴. 将代入+, 得+, ∴+. ∵,, ∴. ∵, ∴, ∴. ∵, ∴, ∴
同课章节目录
