9.1 杠杆 课件(共45张PPT)2022-2023学年北师大版物理八年级下册
文档属性
| 名称 | 9.1 杠杆 课件(共45张PPT)2022-2023学年北师大版物理八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-20 06:25:22 | ||
图片预览







文档简介
(共45张PPT)
第九章 机械与功
第1节 杠杆
北师大版 物理 八年级下册
1、杠杆
2、杠杆平衡条件
学习目标
定义
在力的作用下绕固定点转动的硬棒。
探究新知
新知一 杠杆
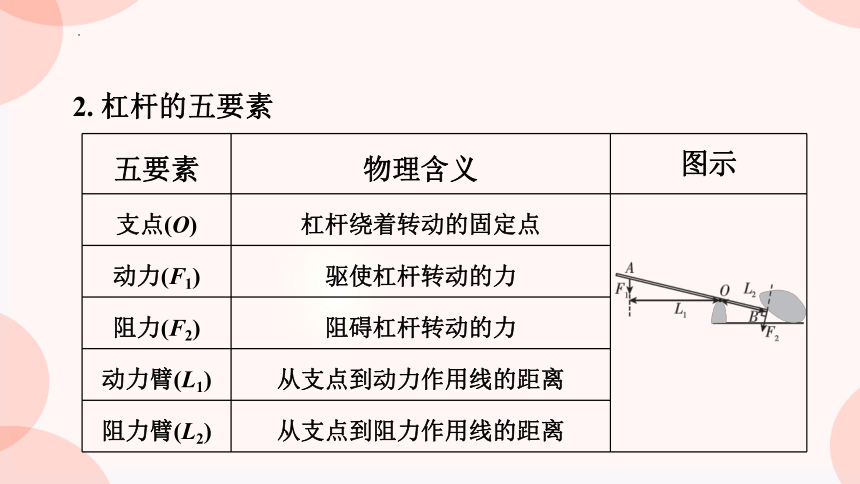
2. 杠杆的五要素
五要素 物理含义 图示
支点(O) 杠杆绕着转动的固定点
动力(F1) 驱使杠杆转动的力 阻力(F2) 阻碍杠杆转动的力 动力臂(L1) 从支点到动力作用线的距离 阻力臂(L2) 从支点到阻力作用线的距离 物理思想
杠杆是从具有复杂外形的机械中抽象出来的理想模型,其本质是一根可以绕固定点转动的硬棒。前面学习的连通器也是一个理想模型。
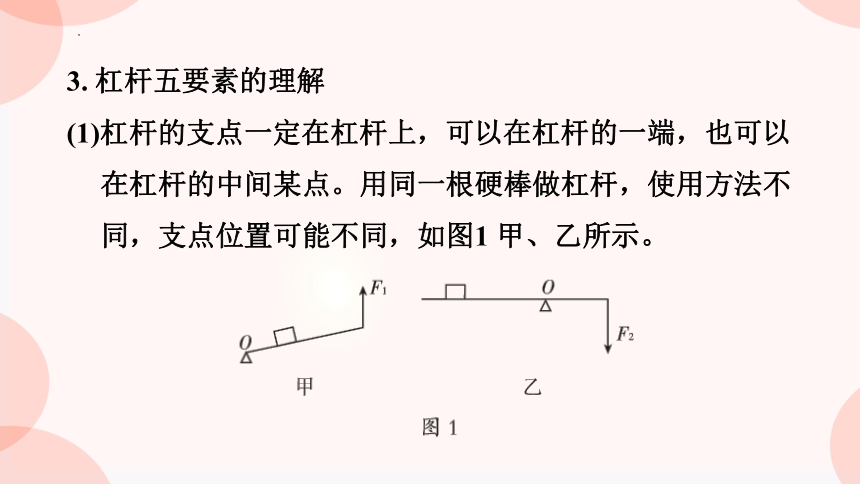
3. 杠杆五要素的理解
(1)杠杆的支点一定在杠杆上,可以在杠杆的一端,也可以在杠杆的中间某点。用同一根硬棒做杠杆,使用方法不同,支点位置可能不同,如图1 甲、乙所示。
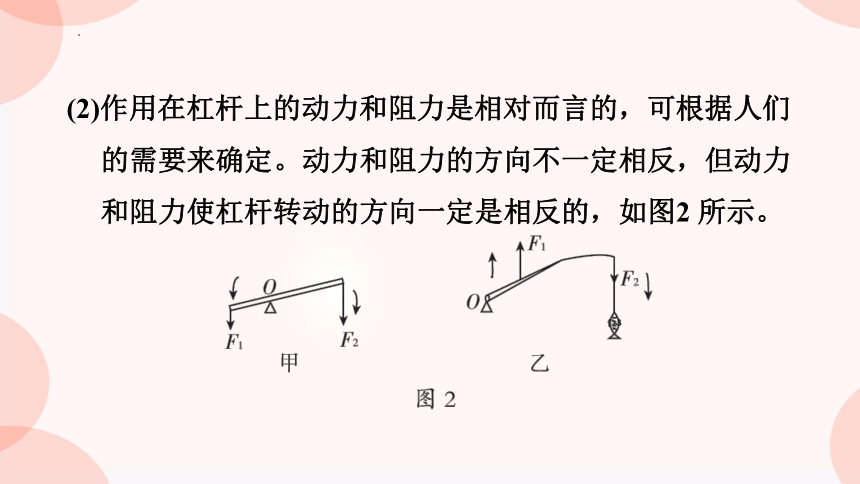
(2)作用在杠杆上的动力和阻力是相对而言的,可根据人们的需要来确定。动力和阻力的方向不一定相反,但动力和阻力使杠杆转动的方向一定是相反的,如图2 所示。
(3)力臂是支点到力的作用线的距离,不是支点到力的作用点的距离,即力臂是点到线的距离,不是点到点的距离。
(4)力臂有时在杠杆上,有时不在杠杆上。
(5)如果力的作用线恰好通过支点,则其力臂为零,此时这个力不能使杠杆转动。
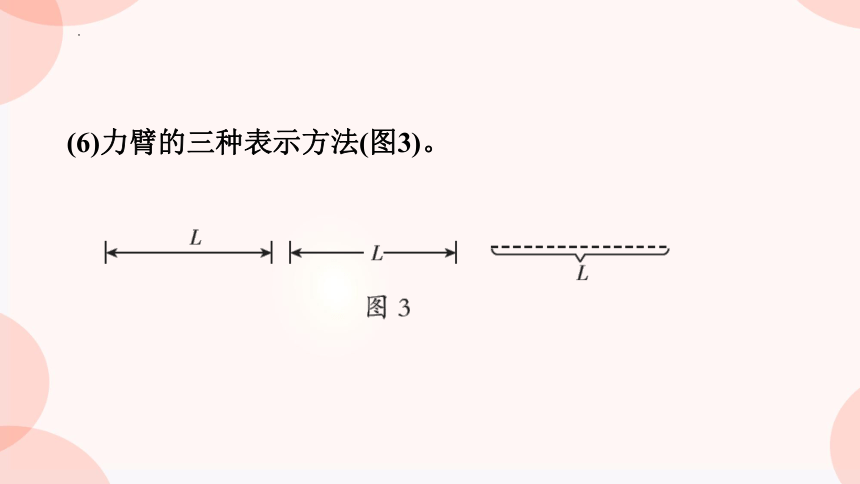
(6)力臂的三种表示方法(图3)。
深度理解
1.杠杆定义中的力是指作用在杠杆上的力,因此杠杆是受力物体。
2.杠杆在力的作用下是绕固定点转动,而不是整体向某个方向运动( 平动)。
3.一根硬棒成为杠杆的条件:
(1) 要有力的作用;(2)能绕着固定点转动;
(3) 杠杆可以是直的,也可以是弯的,但必须是硬的,即在力的作用下不发生或基本不发生形变。
特别提示
支点位置与动力方向、阻力方向的关系:当支点在杠杆的一端时,动力和阻力的方向应该相反;当支点在动力和阻力的作用点之间时,动力和阻力的方向大致相同。
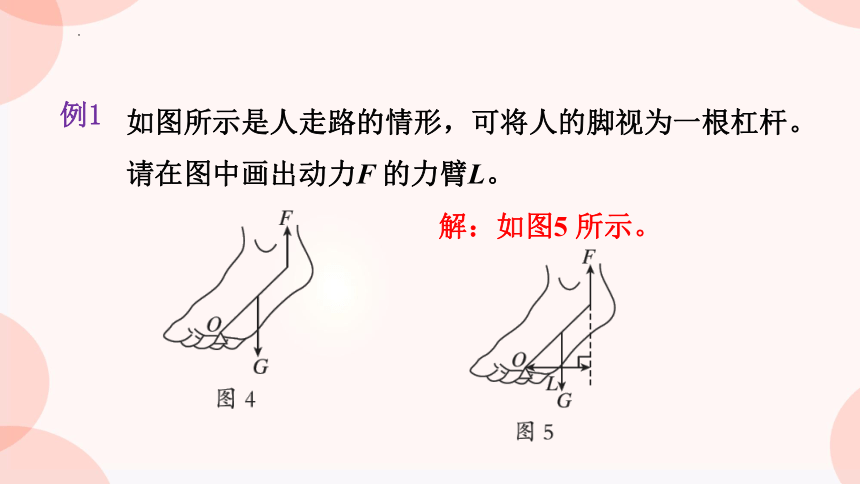
如图所示是人走路的情形,可将人的脚视为一根杠杆。请在图中画出动力F 的力臂L。
解:如图5 所示。
例1
解题秘方:根据力臂的定义,画出“点”到“线”的距离。
解析:从支点O 作力F 作用线的垂线段,即为动力F 的力臂L。
方法技巧
力臂的画法:
1. 确定支点——假设杠杆转动,杠杆上相对静止的点就是支点;
2. 确定动力和阻力的作用线——从动力、阻力作用点沿力的方向(或反方向)分别画线即可得到;
3. 画出动力臂和阻力臂——从支点向动力、阻力的作用线作垂线,支点到垂足间的距离为力臂。
1. 杠杆平衡 在力的作用下,如果杠杆处于静止状态,或绕支点匀速转动,我们就认为杠杆平衡了。
2. 探究杠杆平衡条件
(1)实验器材:杠杆、支架、钩码、刻度尺、细线等。
(2)实验步骤:
①首先调节杠杆两端平衡螺母,使杠杆不挂钩码时,在水平位置平衡。
新知二 杠杆平衡条件
②在杠杆两端挂上不同数量的钩码,移动钩码的位置,使杠杆再次在水平位置平衡,如图6 所示,这时杠杆两端受到的作用力等于各自所挂
钩码受到的重力。
③设右端钩码对杠杆施加的力为动力F1,左端钩码对杠杆施加的力为阻力F2,测出杠杆平衡时的动力臂L1 和阻力臂L2,把F1、L1、F2、L2 的数值填入表格中。
④改变F2 或L2 的大小,相应地调节F1 和L1,再做几次实验,并将得到的实验数据填入表格中。
实验 次数 动力F1/N 动力臂 L1/cm 动力× 动力臂/ (N·cm) 阻力F2/N 阻力臂L2/cm 阻力× 阻力臂/
(N·cm)
1 0.5 30 15 1.0 15 15
2 1.0 20 20 2.0 10 20
3 1.5 20 30 3.0 10 30
(3)实验结论:分析实验数据,发现每次杠杆平衡时,动力、动力臂、阻力、阻力臂可能不一样,但动力与动力臂的乘积等于阻力与阻力臂的乘积,即动力× 动力臂= 阻力× 阻力臂(F1×L1=F2×L2)。
3. 杠杆平衡条件
(1)内容:动力× 动力臂= 阻力× 阻力臂。
(2)字母表示:F1×L1=F2×L2。
(3)说明:当F1L1=F2L2 时,杠杆平衡;当F1L1>F2L2 时,杠杆朝动力F1 的方向转动;当F1L1知识链接
1.实验前要调节杠杆两端的平衡螺母,使杠杆在水平位置平衡,这样做的目的:
(1) 让杠杆的重心刚好在支点上,使重力的力臂为零,以消除杠杆重力对实验的影响;
(2) 当杠杆在水平位置平衡时,力臂恰好与杠杆在同一直线上,这样就可以直接从杠杆上读出力臂的大小。
2.实验过程中,不能调节平衡螺母。
3.杠杆平衡的调节原则:将平衡螺母向杠杆的翘起端调节。
4.杠杆的平衡包含静止和匀速转动两种状态。为了研究方便,我们在探究杠杆平衡时,选择了杠杆平衡状态中的静止状态。
5.影响杠杆转动的因素,不单纯是动力F1和阻力F2的大小关系,也不单纯是动力臂L1和阻力臂L2的大小关系,而是力和力臂的乘积,即F1L1和F2L2的大小关系。
【探究名称】探究杠杆的平衡条件。
【猜想与假设】
猜想一:动力× 动力臂=阻力× 阻力臂;
猜想二:动力× 支点到动力作用点的距离=阻力× 支点到阻力作用点的距离。
例2
解题秘方:试题属于验证性实验题,可以根据实验操作经验和所学知识直接解答。
【设计实验与进行实验】
(1)如图甲所示,应将杠杆两端的螺母向 ________(选填“左”或“右”)调节,使杠杆在水平位置平衡。
左
解析:图甲中杠杆左边高右边低,杠杆的重心偏右,应将平衡螺母向左调节使杠杆的重心移到中间位置。
(2)如图乙所示,小明同学挂上钩码并调节钩码的位置,使杠杆水平平衡,记录的数据如表。
实验次数 动力F1/N OB 间距离/cm 阻力F2/N OA 间距离/cm
小明 1 1.0 5 0.5 10
2 1.5 10 1.0 15
3 1.0 10 2.0 5
小红和 小明 4 0.8 15 1.0 10
5 1.4 15 1.0 10
(3)改变钩码的 ________和钩码的位置重复上述实验两次,记录的数据如表。
个数
解析:为使实验结论更具有普遍性,应多次实验,所以要改变力和力臂的大小,可以通过改变钩码个数改变动力和阻力的大小。
【分析与论证】
根据小明同学的数据可验证猜想 ________ (选填“一”“二”或“一和二”)是正确的。而小红同学则认为小明同学每组数据中的力臂恰好都等于支点到力的作用点的距离,具有一定的特殊性,还应改变动力或阻力的________进行实验。
一和二
方向
于是,小红同学协助小明同学按图丙方式进行实验,获得表中后两组数据。综合分析表中数据可验证猜想 ________是错误的。若要验证另一种猜想是否正
确,必须添加的测量工具是________。
通过以上探究,小明同学真正理解了力
臂是支点到_____________的距离。
二
刻度尺
力的作用线
解析:从实验数据可以证明一和二两种猜想都是正确的;小明实验中当动力和阻力都与力臂垂直时,力臂的大小恰好等于支点到力的作用点的距离,为避免实验的偶然性可以通过改变力的方向使得力臂不等于支点到力的作用点的距离,以此验证猜想二是否正确;通过小红和小明的实验数据可以验证猜想二是错误的;若想验证猜想一是否正确,需要用刻度尺测出正确力臂;通过上述验证可知力臂是支点到力的作用线的距离。
特别提醒
实验中利用钩码而不用弹簧测力计拉杠杆的原因:
1. 方便拉力的计算,F拉=G 钩码;
2. 利用弹簧测力计拉杠杆,不易控制拉力的方向始终竖直向下。
误区警示
不要误认为杠杆平衡条件是:动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离。
杠杆的分类
根据动力臂和阻力臂的关系,可将杠杆分为三类:省力杠杆、等臂杠杆和费力杠杆。
新知三 生活中的杠杆
2. 三类杠杆的比较
省力杠杆 等臂杠杆 费力杠杆
示意图
力臂关系 L1>L2 L1=L2 L1力的关系 F1F2
特点 省力但费距离 不省力也不费力,不省距离也不费距离 费力但省距离
应用 钢丝钳 天平 应用
误区警示
1.不要误认为费力杠杆会费力就没有用处,人们使用费力杠杆可以省距离,比如筷子、钓鱼竿的使用。
2.有些杠杆由于使用方法的不同,有时会省力,有时会费力。如使用图9所示的剪刀,若动力F1 不变,被剪的物体置于a处时,剪刀是省力杠杆,被剪的
物体置于b处时,剪刀是费力杠杆。
3. 轮轴
(1)定义:由具有共同转动轴的大轮和小轮组成的简单机械,如图8 所示(通常把大轮叫轮,小轮叫轴)。
(2)实质:轮轴可以看成一个可连续转
动的杠杆,支点在轮轴的轴线上,
如图8 所示。
(3)公式:F1R=F2r 或 ,即轮半径是轴半径的几倍,则作用在轮上的力就是作用在轴上的力的几分之一。
(4)特点:当动力作用在轮上,阻力作用在轴上时,由于R>r,故F1F2,此时轮轴会费力,也可改变力的方向,但会省距离。
误区警示
不要误认为使用轮轴一定会省力,要看动力是作用在轮上还是作用在轴上。
如图10 所示,是小英用扫帚打扫地面卫生的情景,此时扫帚属于________ (选填“省力”“费力”或“等臂”)杠杆。
费力
例3
解题秘方:画出杠杆的示意图,再根据动力臂L1 和阻力臂L2 的大小关系判断杠杆的类型,或根据杠杆的使用特点判断杠杆的类型。
方法技巧
判断杠杆类型的两种方法:
1. 根据动力臂L1和阻力臂L2的长短关系判断;
2. 根据应用目的和效果判断:省力杠杆一般在阻力大的情况下使用,费力杠杆一般在阻力小的情况下为了省距离而使用。
解析:方法一:扫地时,扫帚相当于一
个杠杆,其示意图如图11 所示,可见其
属于费力杠杆。方法二:用扫帚扫地时,
手移动较小的距离,可以扫过较大的面
积,根据杠杆的使用特点知扫帚属于费
力杠杆。
一、杠杆
杠杆
定义
能绕固定点转动的硬棒
平衡条件
分类
F1L1= F2L2
省力杠杆
费力杠杆
等臂杠杆
归纳新知
再 见
第九章 机械与功
第1节 杠杆
北师大版 物理 八年级下册
1、杠杆
2、杠杆平衡条件
学习目标
定义
在力的作用下绕固定点转动的硬棒。
探究新知
新知一 杠杆
2. 杠杆的五要素
五要素 物理含义 图示
支点(O) 杠杆绕着转动的固定点
动力(F1) 驱使杠杆转动的力 阻力(F2) 阻碍杠杆转动的力 动力臂(L1) 从支点到动力作用线的距离 阻力臂(L2) 从支点到阻力作用线的距离 物理思想
杠杆是从具有复杂外形的机械中抽象出来的理想模型,其本质是一根可以绕固定点转动的硬棒。前面学习的连通器也是一个理想模型。
3. 杠杆五要素的理解
(1)杠杆的支点一定在杠杆上,可以在杠杆的一端,也可以在杠杆的中间某点。用同一根硬棒做杠杆,使用方法不同,支点位置可能不同,如图1 甲、乙所示。
(2)作用在杠杆上的动力和阻力是相对而言的,可根据人们的需要来确定。动力和阻力的方向不一定相反,但动力和阻力使杠杆转动的方向一定是相反的,如图2 所示。
(3)力臂是支点到力的作用线的距离,不是支点到力的作用点的距离,即力臂是点到线的距离,不是点到点的距离。
(4)力臂有时在杠杆上,有时不在杠杆上。
(5)如果力的作用线恰好通过支点,则其力臂为零,此时这个力不能使杠杆转动。
(6)力臂的三种表示方法(图3)。
深度理解
1.杠杆定义中的力是指作用在杠杆上的力,因此杠杆是受力物体。
2.杠杆在力的作用下是绕固定点转动,而不是整体向某个方向运动( 平动)。
3.一根硬棒成为杠杆的条件:
(1) 要有力的作用;(2)能绕着固定点转动;
(3) 杠杆可以是直的,也可以是弯的,但必须是硬的,即在力的作用下不发生或基本不发生形变。
特别提示
支点位置与动力方向、阻力方向的关系:当支点在杠杆的一端时,动力和阻力的方向应该相反;当支点在动力和阻力的作用点之间时,动力和阻力的方向大致相同。
如图所示是人走路的情形,可将人的脚视为一根杠杆。请在图中画出动力F 的力臂L。
解:如图5 所示。
例1
解题秘方:根据力臂的定义,画出“点”到“线”的距离。
解析:从支点O 作力F 作用线的垂线段,即为动力F 的力臂L。
方法技巧
力臂的画法:
1. 确定支点——假设杠杆转动,杠杆上相对静止的点就是支点;
2. 确定动力和阻力的作用线——从动力、阻力作用点沿力的方向(或反方向)分别画线即可得到;
3. 画出动力臂和阻力臂——从支点向动力、阻力的作用线作垂线,支点到垂足间的距离为力臂。
1. 杠杆平衡 在力的作用下,如果杠杆处于静止状态,或绕支点匀速转动,我们就认为杠杆平衡了。
2. 探究杠杆平衡条件
(1)实验器材:杠杆、支架、钩码、刻度尺、细线等。
(2)实验步骤:
①首先调节杠杆两端平衡螺母,使杠杆不挂钩码时,在水平位置平衡。
新知二 杠杆平衡条件
②在杠杆两端挂上不同数量的钩码,移动钩码的位置,使杠杆再次在水平位置平衡,如图6 所示,这时杠杆两端受到的作用力等于各自所挂
钩码受到的重力。
③设右端钩码对杠杆施加的力为动力F1,左端钩码对杠杆施加的力为阻力F2,测出杠杆平衡时的动力臂L1 和阻力臂L2,把F1、L1、F2、L2 的数值填入表格中。
④改变F2 或L2 的大小,相应地调节F1 和L1,再做几次实验,并将得到的实验数据填入表格中。
实验 次数 动力F1/N 动力臂 L1/cm 动力× 动力臂/ (N·cm) 阻力F2/N 阻力臂L2/cm 阻力× 阻力臂/
(N·cm)
1 0.5 30 15 1.0 15 15
2 1.0 20 20 2.0 10 20
3 1.5 20 30 3.0 10 30
(3)实验结论:分析实验数据,发现每次杠杆平衡时,动力、动力臂、阻力、阻力臂可能不一样,但动力与动力臂的乘积等于阻力与阻力臂的乘积,即动力× 动力臂= 阻力× 阻力臂(F1×L1=F2×L2)。
3. 杠杆平衡条件
(1)内容:动力× 动力臂= 阻力× 阻力臂。
(2)字母表示:F1×L1=F2×L2。
(3)说明:当F1L1=F2L2 时,杠杆平衡;当F1L1>F2L2 时,杠杆朝动力F1 的方向转动;当F1L1
1.实验前要调节杠杆两端的平衡螺母,使杠杆在水平位置平衡,这样做的目的:
(1) 让杠杆的重心刚好在支点上,使重力的力臂为零,以消除杠杆重力对实验的影响;
(2) 当杠杆在水平位置平衡时,力臂恰好与杠杆在同一直线上,这样就可以直接从杠杆上读出力臂的大小。
2.实验过程中,不能调节平衡螺母。
3.杠杆平衡的调节原则:将平衡螺母向杠杆的翘起端调节。
4.杠杆的平衡包含静止和匀速转动两种状态。为了研究方便,我们在探究杠杆平衡时,选择了杠杆平衡状态中的静止状态。
5.影响杠杆转动的因素,不单纯是动力F1和阻力F2的大小关系,也不单纯是动力臂L1和阻力臂L2的大小关系,而是力和力臂的乘积,即F1L1和F2L2的大小关系。
【探究名称】探究杠杆的平衡条件。
【猜想与假设】
猜想一:动力× 动力臂=阻力× 阻力臂;
猜想二:动力× 支点到动力作用点的距离=阻力× 支点到阻力作用点的距离。
例2
解题秘方:试题属于验证性实验题,可以根据实验操作经验和所学知识直接解答。
【设计实验与进行实验】
(1)如图甲所示,应将杠杆两端的螺母向 ________(选填“左”或“右”)调节,使杠杆在水平位置平衡。
左
解析:图甲中杠杆左边高右边低,杠杆的重心偏右,应将平衡螺母向左调节使杠杆的重心移到中间位置。
(2)如图乙所示,小明同学挂上钩码并调节钩码的位置,使杠杆水平平衡,记录的数据如表。
实验次数 动力F1/N OB 间距离/cm 阻力F2/N OA 间距离/cm
小明 1 1.0 5 0.5 10
2 1.5 10 1.0 15
3 1.0 10 2.0 5
小红和 小明 4 0.8 15 1.0 10
5 1.4 15 1.0 10
(3)改变钩码的 ________和钩码的位置重复上述实验两次,记录的数据如表。
个数
解析:为使实验结论更具有普遍性,应多次实验,所以要改变力和力臂的大小,可以通过改变钩码个数改变动力和阻力的大小。
【分析与论证】
根据小明同学的数据可验证猜想 ________ (选填“一”“二”或“一和二”)是正确的。而小红同学则认为小明同学每组数据中的力臂恰好都等于支点到力的作用点的距离,具有一定的特殊性,还应改变动力或阻力的________进行实验。
一和二
方向
于是,小红同学协助小明同学按图丙方式进行实验,获得表中后两组数据。综合分析表中数据可验证猜想 ________是错误的。若要验证另一种猜想是否正
确,必须添加的测量工具是________。
通过以上探究,小明同学真正理解了力
臂是支点到_____________的距离。
二
刻度尺
力的作用线
解析:从实验数据可以证明一和二两种猜想都是正确的;小明实验中当动力和阻力都与力臂垂直时,力臂的大小恰好等于支点到力的作用点的距离,为避免实验的偶然性可以通过改变力的方向使得力臂不等于支点到力的作用点的距离,以此验证猜想二是否正确;通过小红和小明的实验数据可以验证猜想二是错误的;若想验证猜想一是否正确,需要用刻度尺测出正确力臂;通过上述验证可知力臂是支点到力的作用线的距离。
特别提醒
实验中利用钩码而不用弹簧测力计拉杠杆的原因:
1. 方便拉力的计算,F拉=G 钩码;
2. 利用弹簧测力计拉杠杆,不易控制拉力的方向始终竖直向下。
误区警示
不要误认为杠杆平衡条件是:动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离。
杠杆的分类
根据动力臂和阻力臂的关系,可将杠杆分为三类:省力杠杆、等臂杠杆和费力杠杆。
新知三 生活中的杠杆
2. 三类杠杆的比较
省力杠杆 等臂杠杆 费力杠杆
示意图
力臂关系 L1>L2 L1=L2 L1
特点 省力但费距离 不省力也不费力,不省距离也不费距离 费力但省距离
应用 钢丝钳 天平 应用
误区警示
1.不要误认为费力杠杆会费力就没有用处,人们使用费力杠杆可以省距离,比如筷子、钓鱼竿的使用。
2.有些杠杆由于使用方法的不同,有时会省力,有时会费力。如使用图9所示的剪刀,若动力F1 不变,被剪的物体置于a处时,剪刀是省力杠杆,被剪的
物体置于b处时,剪刀是费力杠杆。
3. 轮轴
(1)定义:由具有共同转动轴的大轮和小轮组成的简单机械,如图8 所示(通常把大轮叫轮,小轮叫轴)。
(2)实质:轮轴可以看成一个可连续转
动的杠杆,支点在轮轴的轴线上,
如图8 所示。
(3)公式:F1R=F2r 或 ,即轮半径是轴半径的几倍,则作用在轮上的力就是作用在轴上的力的几分之一。
(4)特点:当动力作用在轮上,阻力作用在轴上时,由于R>r,故F1
误区警示
不要误认为使用轮轴一定会省力,要看动力是作用在轮上还是作用在轴上。
如图10 所示,是小英用扫帚打扫地面卫生的情景,此时扫帚属于________ (选填“省力”“费力”或“等臂”)杠杆。
费力
例3
解题秘方:画出杠杆的示意图,再根据动力臂L1 和阻力臂L2 的大小关系判断杠杆的类型,或根据杠杆的使用特点判断杠杆的类型。
方法技巧
判断杠杆类型的两种方法:
1. 根据动力臂L1和阻力臂L2的长短关系判断;
2. 根据应用目的和效果判断:省力杠杆一般在阻力大的情况下使用,费力杠杆一般在阻力小的情况下为了省距离而使用。
解析:方法一:扫地时,扫帚相当于一
个杠杆,其示意图如图11 所示,可见其
属于费力杠杆。方法二:用扫帚扫地时,
手移动较小的距离,可以扫过较大的面
积,根据杠杆的使用特点知扫帚属于费
力杠杆。
一、杠杆
杠杆
定义
能绕固定点转动的硬棒
平衡条件
分类
F1L1= F2L2
省力杠杆
费力杠杆
等臂杠杆
归纳新知
再 见
