中考数学模拟试卷(11)(含答案)
图片预览


文档简介
2014年中考模拟试卷 数学卷
考生须知:
1.本试卷分试题卷和答题卷两部分,满分120分,考试时间120分钟。
2.答题时,应该在答题卷指定位置内写明校名,姓名和准考证号。
3.所有答案都必须做在答题卷标定的位置上,请务必注意试题序号和答题序号相对应。
4.考试结束后,上交试题卷和答题卷
试题卷
一. 仔细选一选(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的。注意可以用多种不同的方法来选取正确答案。
1.的相反数是( )(原创)
A. B. C. D.
2.下列运算正确的是( ) (改编)
A. B. C. D.
3.北京时间2010年10月1日长征三号丙火箭在位于中国四川的西昌卫星发射中心发发射,把嫦娥二号探月卫星成功送入太空。“嫦娥二号”所携带的CCD立体相机的空间分辨率小于10米,并将在距月球约100公里的轨道上绕月运行,较“嫦娥一号”的距月球200公里高的轨道要低,也就是卫星轨道距月球表面又近了一倍,“看得更加精细”。“200公里”用科学计数法表示为( ) (原创)
A.2.00×102米 B.2.00×105米 C.200×103米 D.2.00×104米
4.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5.为了解初三学生的体育锻炼时间,小华调查了某班
45名同学一周参加体育锻炼的情况,并把它绘制成折线
统计图.那么关于该班45名同学一周参加体育锻炼时
间的说法错误的是( )(改编)
A.众数是9 B.中位数是9
C.平均数是9 D.锻炼时间不低于9小时的有14人
6.如图所示的正方体,用一个平面截去它的一个角,则截面不可能是( )(改编)
A.锐角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
7. .如图是小明在物理实验课上用量筒和水测量铁块A的体积实验,小明在匀速向上将铁块提起,直至铁块完全露出水面一定高度的过程中,则下图能反映液面高度h与铁块被提起的时间t之间的函数关系的大致图象是 ( )
8.一个正偶数的算术平方根是,那么与这个正偶数相邻的下一个正偶数的算术平方根( )。(原创)
A. B. C. D.
9. 如图,边长为的六角螺帽在桌面上滚动(没有滑动)
一周,则它的中心点所经过的路径长为( )
A. B.
C. D.
10. 如图,将平面直角坐标系中的△AOB绕点O顺时针旋转90°得△A′OB′.已知∠AOB=60°,∠B=90°,AB=,则点B′的坐标是(A) (B) (C) (D)
二. 认真填一填(本题有6个小题,每小题4分,共24分)
要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案
11.请从中,任选两式做差得到的一个式子进行因式分解是______(原创)
12.已知正整数a满足不等式组 (为未知数)无解,则函数图象与轴的坐标为 (原创)
13.如图,小明在A时测得某树的影长为3米,B时又测得该树的影长为
12米,若两次日照的光线互相垂直,则树的高度为_____米.(改编)
14. 如图,在中,为⊙的直径,,则sin=____________(原创)
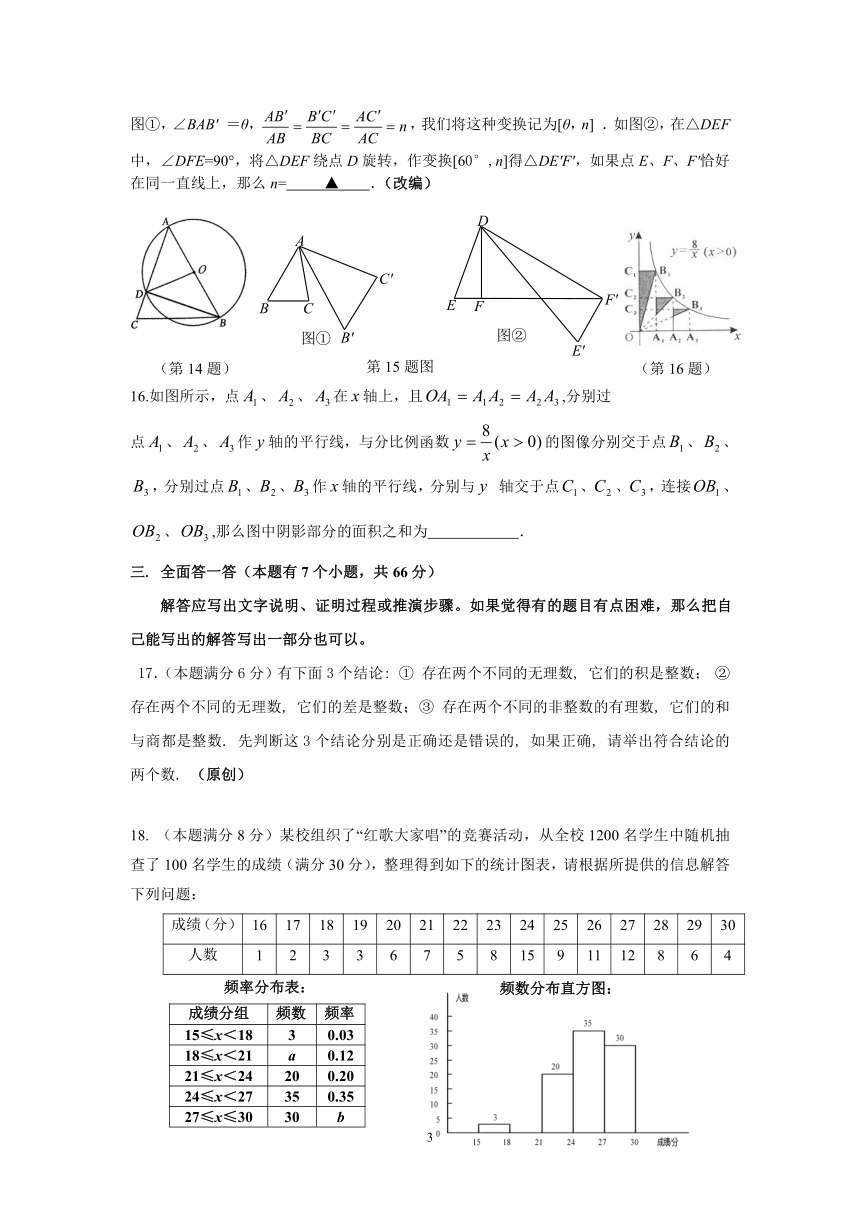
15.将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍得△AB′ C′ ,即如图①,∠BAB′ =θ,,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= ▲ .(改编)
16.如图所示,点、、在轴上,且,分别过点、、作轴的平行线,与分比例函数的图像分别交于点、、,分别过点、、作轴的平行线,分别与 轴交于点、、,连接、、,那么图中阴影部分的面积之和为 .
三. 全面答一答(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤。如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以。
17.(本题满分6分)有下面3个结论: ① 存在两个不同的无理数, 它们的积是整数; ② 存在两个不同的无理数, 它们的差是整数; ③ 存在两个不同的非整数的有理数, 它们的和与商都是整数. 先判断这3个结论分别是正确还是错误的, 如果正确, 请举出符合结论的两个数. (原创)
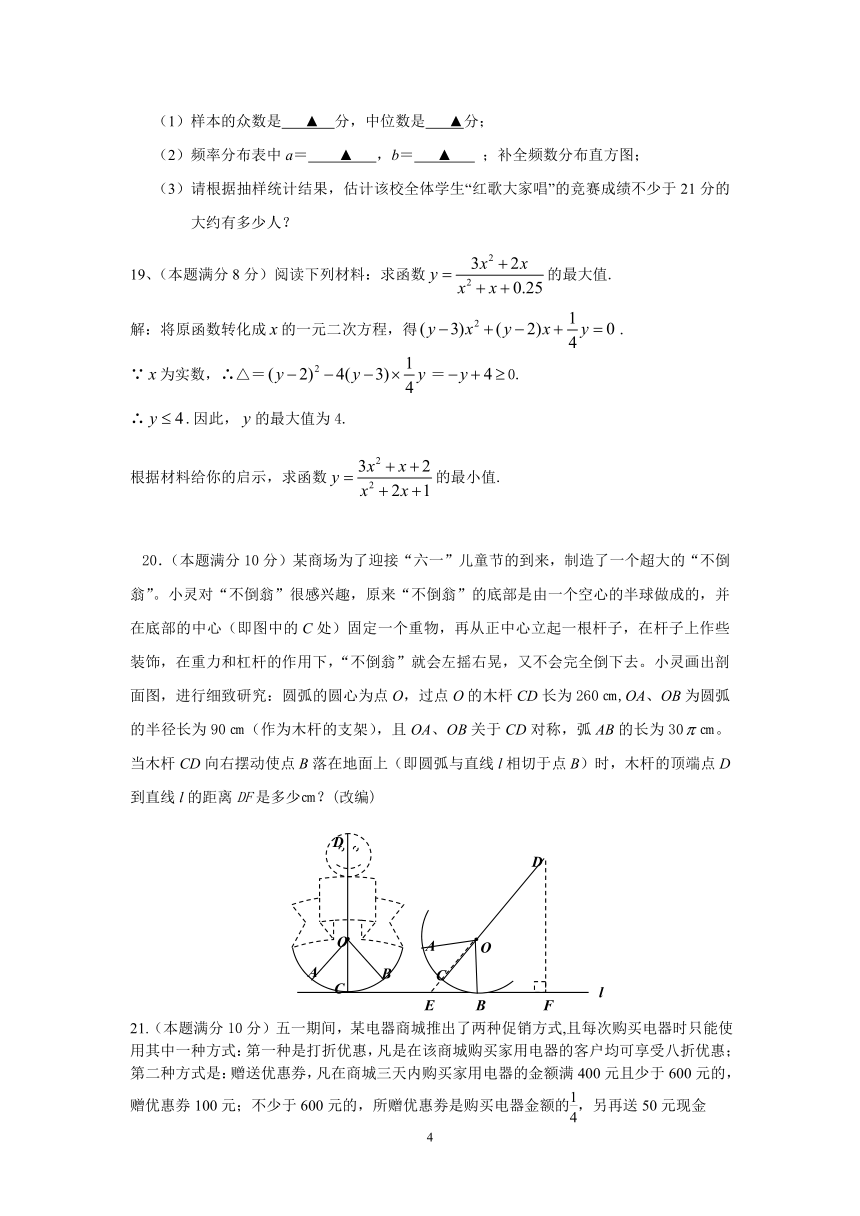
18. (本题满分8分)某校组织了“红歌大家唱”的竞赛活动,从全校1200名学生中随机抽查了100名学生的成绩(满分30分),整理得到如下的统计图表,请根据所提供的信息解答下列问题:
成绩(分) 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
人数 1 2 3 3 6 7 5 8 15 9 11 12 8 6 4
(1)样本的众数是 ▲ 分,中位数是 ▲ 分;
(2)频率分布表中a= ▲ ,b= ▲ ;补全频数分布直方图;
(3)请根据抽样统计结果,估计该校全体学生“红歌大家唱”的竞赛成绩不少于21分的大约有多少人?
19、(本题满分8分)阅读下列材料:求函数的最大值.
解:将原函数转化成的一元二次方程,得.
∵为实数,∴△==0.
∴.因此,的最大值为4.
根据材料给你的启示,求函数的最小值.
20.(本题满分10分)某商场为了迎接“六一”儿童节的到来,制造了一个超大的“不倒翁”。小灵对“不倒翁”很感兴趣,原来“不倒翁”的底部是由一个空心的半球做成的,并在底部的中心(即图中的C处)固定一个重物,再从正中心立起一根杆子,在杆子上作些装饰,在重力和杠杆的作用下,“不倒翁”就会左摇右晃,又不会完全倒下去。小灵画出剖面图,进行细致研究:圆弧的圆心为点O,过点O的木杆CD长为260㎝,OA、OB为圆弧的半径长为90㎝(作为木杆的支架),且OA、OB关于CD对称,弧AB的长为30㎝。当木杆CD向右摆动使点B落在地面上(即圆弧与直线l相切于点B)时,木杆的顶端点D到直线l的距离DF是多少㎝?(改编)
21.(本题满分10分)五一期间,某电器商城推出了两种促销方式,且每次购买电器时只能使用其中一种方式:第一种是打折优惠,凡是在该商城购买家用电器的客户均可享受八折优惠;第二种方式是:赠送优惠券,凡在商城三天内购买家用电器的金额满400元且少于600元的,赠优惠券100元;不少于600元的,所赠优惠劵是购买电器金额的,另再送50元现金
(1)以上两种促销方式中第二种方式,可用如下形式表达:设购买电器的金额为x(x≥400)元,优惠券金额为y元,则:①当x=500时,y= ;②当x≥600时,y= ;
(2)如果小张想一次性购买原价为x(400≤x<600)元的电器,可以使用优惠劵,在上面的两种促销方式中,试通过计算帮他确定一种比较合算的方式?
(3)如果小张在促销期间内在此商城先后两次购买电器时都得到了优惠券(两次购买均未使用优惠券),第一次购买金额在600元以内,第二次购买金额超过600元,所得优惠券金额累计达800元,设他购买电器的金额为W元,W至少应为多少?(W=支付金额-所送现金金额) (改编)
22.(满分12分)将军家俱市场现有大批如图所示的边角余料
(单位:cm)城西中学数学兴趣小组决定将其加工成等腰三角形,
且方案如下:
(1)三角形中至少有一边长为10 cm;
(2)三角形中至少有一边上的高为8 cm
请在备用图上画出出分割线,并求出相应图形面积
(第22题)
23. (本题满分12分)
在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
2014年中考模拟试卷
数学参考答案及评分标准
一.仔细选一选(本题有10个小题,每小题3分,共30分)。
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B C D B C C A
二.认真填一填(本题有6个小题,每小题4分,共24分)
11. 答案不唯一 12 . 13 . 6 14.
15 . 2 16
三. 全面答一答(本题有8个小题,共66分)
17.(本题满分6分)(6分)均正确。
每个反例给2分
举说明
18. (本题满分8分)
解:解:(1)24,24.5 2分
(2)12;0.3,小长方形的高是12(图略) 3分
(3)=1 020. 3分
19.(本题满分8分)
将原函数转化成x的一元二次方程,得(y-3)x2+(2y-1)x+y-2=0, 3分
∵x为实数,
∴△=(2y-1)2-4(y-3)(y-2)=16y-23≥0, 3分
y≥ 16/23 2分
20.(本题满分10分)、
解:由弧AB的长可得,∠AOB=60°,
从而∠BOE=∠COB=30°,(2分)
∵OB=90cm,
∴OE=cm,(3分)
∴DE=170+ cm, (2分)
∴DF=180+ cm (3分)
21.(本题满分10分)
解:(1)y=100;y=x (2分)
(2)设y1=0.8x,y2=x-100,
由0.8x=x-100得x=500,此时y1=y2;当400≤x<500时y1>y2;当500<x<600时y1<y2;
∴当x=500时,两种方式一样合算;当400≤x<500时,选第二种方式合算;当500<x<600时,选第一种方式合算 (3分)
(3)设第一次购买花了m元,第二次花了n元
当400≤m<600,n≥600时,100+n=800,得n=2800
W=m+n-50=m+2750
∵400≤m<600,∴3150≤W<3350
∴W至少为3150 (3分)
22.(满分12分)
解:由勾股定理得:AB=则
如图(1)AD=AB=10 cm时,BD=6 cm,S==48 cm; ( 4分)
如图(2)BD=AB=10 cm时,S==40cm (4分)
如图(3)线段AB的垂直平分线交BC延长线于点D,则AB=10,设DC=x,则AD=BD=6+x,
在Rt△ACD中,S==;
答:可以设计出面积分别为48 cm、40cm和 cm的等腰三角形 (4分)
23.(本小题12分)
解:(1)在Rt△ABC中,∠A=90°,AB=6,AC=8 ∴BC=10……………………(1分)
点D为BC的中点 ∴CD=5
可证△ABC∽△DEC
∴, 即………………………………(1分)
∴,……………………………………………………(1分)
(2)①当点P在AB边上时,在Rt△ABC中,∠B+∠C=90°,
在Rt△EDC中,∠DEC+∠C=90°, ∴∠DEC=∠B
∵DE⊥BC,∠PDQ=90° ∴∠PDQ=∠BDE=90° ∴∠BDP=∠EDQ
∴△BPD∽△EQD ……………………………………………………………(1分)
∴, 即,
∴ ………………………………………………………………………(1分)
∴CQ=EC-EQ……………………………………………………………(1分)
②当点P在AB的延长线上时,同理可得:,
∴CQ=EC+EQ …………………………………………………………(1分)
(3)∵线段PQ与线段DE的交点为点F,∴点P在边AB上
∵△BPD∽△EQD ∴
若设BP=x ,则, …………………………………(1分) 可得 ∴∠QPD=∠C
又可证∠PDE=∠CDQ ∴△PDF∽△CDQ
∵△PDF为等腰三角形 ∴△CDQ为等腰三角形………………………(1分)
①当CQ=CD时,可得: 解得:………………………(1分)
②当QC=QD时, 过点Q作QM⊥CB于M,
∴,
∴, 解得 ……………………………………………(1分)
③当DC=DQ时,过点D作DN⊥CQ于N,
∴,
∴, 解得(不合题意,舍去)…………………………(1分)
∴综上所述,或
8
(第6题)
(第9题)
(第10题)
(第13题)
A时
B时
A
B
C
B′
第15题图
C′
D
E
E′
F′
F
图①
图②
(第16题)
(第14题)
成绩分组 频数 频率
15≤x<18 3 0.03
18≤x<21 a 0.12
21≤x<24 20 0.20
24≤x<27 35 0.35
27≤x≤30 30 b
频数分布直方图:
频率分布表:
O
A
B
D
l
A
C
C
D
E
B
F
O
6cm
6. 5cm
8cm
A
B
C
6cm
6. 5cm
8cm
A
B
C
6cm
6. 5cm
8cm
A
B
C
A
B
E
C
D
A
B
C
E
D
第25题图
(备用图)
6cm
6cm
A
B
C
D
8cm
6cm
4cm
A
B
C
D
8cm
A
B
D
8cm
C
PAGE
7
考生须知:
1.本试卷分试题卷和答题卷两部分,满分120分,考试时间120分钟。
2.答题时,应该在答题卷指定位置内写明校名,姓名和准考证号。
3.所有答案都必须做在答题卷标定的位置上,请务必注意试题序号和答题序号相对应。
4.考试结束后,上交试题卷和答题卷
试题卷
一. 仔细选一选(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的。注意可以用多种不同的方法来选取正确答案。
1.的相反数是( )(原创)
A. B. C. D.
2.下列运算正确的是( ) (改编)
A. B. C. D.
3.北京时间2010年10月1日长征三号丙火箭在位于中国四川的西昌卫星发射中心发发射,把嫦娥二号探月卫星成功送入太空。“嫦娥二号”所携带的CCD立体相机的空间分辨率小于10米,并将在距月球约100公里的轨道上绕月运行,较“嫦娥一号”的距月球200公里高的轨道要低,也就是卫星轨道距月球表面又近了一倍,“看得更加精细”。“200公里”用科学计数法表示为( ) (原创)
A.2.00×102米 B.2.00×105米 C.200×103米 D.2.00×104米
4.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5.为了解初三学生的体育锻炼时间,小华调查了某班
45名同学一周参加体育锻炼的情况,并把它绘制成折线
统计图.那么关于该班45名同学一周参加体育锻炼时
间的说法错误的是( )(改编)
A.众数是9 B.中位数是9
C.平均数是9 D.锻炼时间不低于9小时的有14人
6.如图所示的正方体,用一个平面截去它的一个角,则截面不可能是( )(改编)
A.锐角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
7. .如图是小明在物理实验课上用量筒和水测量铁块A的体积实验,小明在匀速向上将铁块提起,直至铁块完全露出水面一定高度的过程中,则下图能反映液面高度h与铁块被提起的时间t之间的函数关系的大致图象是 ( )
8.一个正偶数的算术平方根是,那么与这个正偶数相邻的下一个正偶数的算术平方根( )。(原创)
A. B. C. D.
9. 如图,边长为的六角螺帽在桌面上滚动(没有滑动)
一周,则它的中心点所经过的路径长为( )
A. B.
C. D.
10. 如图,将平面直角坐标系中的△AOB绕点O顺时针旋转90°得△A′OB′.已知∠AOB=60°,∠B=90°,AB=,则点B′的坐标是(A) (B) (C) (D)
二. 认真填一填(本题有6个小题,每小题4分,共24分)
要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案
11.请从中,任选两式做差得到的一个式子进行因式分解是______(原创)
12.已知正整数a满足不等式组 (为未知数)无解,则函数图象与轴的坐标为 (原创)
13.如图,小明在A时测得某树的影长为3米,B时又测得该树的影长为
12米,若两次日照的光线互相垂直,则树的高度为_____米.(改编)
14. 如图,在中,为⊙的直径,,则sin=____________(原创)
15.将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍得△AB′ C′ ,即如图①,∠BAB′ =θ,,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= ▲ .(改编)
16.如图所示,点、、在轴上,且,分别过点、、作轴的平行线,与分比例函数的图像分别交于点、、,分别过点、、作轴的平行线,分别与 轴交于点、、,连接、、,那么图中阴影部分的面积之和为 .
三. 全面答一答(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤。如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以。
17.(本题满分6分)有下面3个结论: ① 存在两个不同的无理数, 它们的积是整数; ② 存在两个不同的无理数, 它们的差是整数; ③ 存在两个不同的非整数的有理数, 它们的和与商都是整数. 先判断这3个结论分别是正确还是错误的, 如果正确, 请举出符合结论的两个数. (原创)
18. (本题满分8分)某校组织了“红歌大家唱”的竞赛活动,从全校1200名学生中随机抽查了100名学生的成绩(满分30分),整理得到如下的统计图表,请根据所提供的信息解答下列问题:
成绩(分) 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
人数 1 2 3 3 6 7 5 8 15 9 11 12 8 6 4
(1)样本的众数是 ▲ 分,中位数是 ▲ 分;
(2)频率分布表中a= ▲ ,b= ▲ ;补全频数分布直方图;
(3)请根据抽样统计结果,估计该校全体学生“红歌大家唱”的竞赛成绩不少于21分的大约有多少人?
19、(本题满分8分)阅读下列材料:求函数的最大值.
解:将原函数转化成的一元二次方程,得.
∵为实数,∴△==0.
∴.因此,的最大值为4.
根据材料给你的启示,求函数的最小值.
20.(本题满分10分)某商场为了迎接“六一”儿童节的到来,制造了一个超大的“不倒翁”。小灵对“不倒翁”很感兴趣,原来“不倒翁”的底部是由一个空心的半球做成的,并在底部的中心(即图中的C处)固定一个重物,再从正中心立起一根杆子,在杆子上作些装饰,在重力和杠杆的作用下,“不倒翁”就会左摇右晃,又不会完全倒下去。小灵画出剖面图,进行细致研究:圆弧的圆心为点O,过点O的木杆CD长为260㎝,OA、OB为圆弧的半径长为90㎝(作为木杆的支架),且OA、OB关于CD对称,弧AB的长为30㎝。当木杆CD向右摆动使点B落在地面上(即圆弧与直线l相切于点B)时,木杆的顶端点D到直线l的距离DF是多少㎝?(改编)
21.(本题满分10分)五一期间,某电器商城推出了两种促销方式,且每次购买电器时只能使用其中一种方式:第一种是打折优惠,凡是在该商城购买家用电器的客户均可享受八折优惠;第二种方式是:赠送优惠券,凡在商城三天内购买家用电器的金额满400元且少于600元的,赠优惠券100元;不少于600元的,所赠优惠劵是购买电器金额的,另再送50元现金
(1)以上两种促销方式中第二种方式,可用如下形式表达:设购买电器的金额为x(x≥400)元,优惠券金额为y元,则:①当x=500时,y= ;②当x≥600时,y= ;
(2)如果小张想一次性购买原价为x(400≤x<600)元的电器,可以使用优惠劵,在上面的两种促销方式中,试通过计算帮他确定一种比较合算的方式?
(3)如果小张在促销期间内在此商城先后两次购买电器时都得到了优惠券(两次购买均未使用优惠券),第一次购买金额在600元以内,第二次购买金额超过600元,所得优惠券金额累计达800元,设他购买电器的金额为W元,W至少应为多少?(W=支付金额-所送现金金额) (改编)
22.(满分12分)将军家俱市场现有大批如图所示的边角余料
(单位:cm)城西中学数学兴趣小组决定将其加工成等腰三角形,
且方案如下:
(1)三角形中至少有一边长为10 cm;
(2)三角形中至少有一边上的高为8 cm
请在备用图上画出出分割线,并求出相应图形面积
(第22题)
23. (本题满分12分)
在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
2014年中考模拟试卷
数学参考答案及评分标准
一.仔细选一选(本题有10个小题,每小题3分,共30分)。
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B C D B C C A
二.认真填一填(本题有6个小题,每小题4分,共24分)
11. 答案不唯一 12 . 13 . 6 14.
15 . 2 16
三. 全面答一答(本题有8个小题,共66分)
17.(本题满分6分)(6分)均正确。
每个反例给2分
举说明
18. (本题满分8分)
解:解:(1)24,24.5 2分
(2)12;0.3,小长方形的高是12(图略) 3分
(3)=1 020. 3分
19.(本题满分8分)
将原函数转化成x的一元二次方程,得(y-3)x2+(2y-1)x+y-2=0, 3分
∵x为实数,
∴△=(2y-1)2-4(y-3)(y-2)=16y-23≥0, 3分
y≥ 16/23 2分
20.(本题满分10分)、
解:由弧AB的长可得,∠AOB=60°,
从而∠BOE=∠COB=30°,(2分)
∵OB=90cm,
∴OE=cm,(3分)
∴DE=170+ cm, (2分)
∴DF=180+ cm (3分)
21.(本题满分10分)
解:(1)y=100;y=x (2分)
(2)设y1=0.8x,y2=x-100,
由0.8x=x-100得x=500,此时y1=y2;当400≤x<500时y1>y2;当500<x<600时y1<y2;
∴当x=500时,两种方式一样合算;当400≤x<500时,选第二种方式合算;当500<x<600时,选第一种方式合算 (3分)
(3)设第一次购买花了m元,第二次花了n元
当400≤m<600,n≥600时,100+n=800,得n=2800
W=m+n-50=m+2750
∵400≤m<600,∴3150≤W<3350
∴W至少为3150 (3分)
22.(满分12分)
解:由勾股定理得:AB=则
如图(1)AD=AB=10 cm时,BD=6 cm,S==48 cm; ( 4分)
如图(2)BD=AB=10 cm时,S==40cm (4分)
如图(3)线段AB的垂直平分线交BC延长线于点D,则AB=10,设DC=x,则AD=BD=6+x,
在Rt△ACD中,S==;
答:可以设计出面积分别为48 cm、40cm和 cm的等腰三角形 (4分)
23.(本小题12分)
解:(1)在Rt△ABC中,∠A=90°,AB=6,AC=8 ∴BC=10……………………(1分)
点D为BC的中点 ∴CD=5
可证△ABC∽△DEC
∴, 即………………………………(1分)
∴,……………………………………………………(1分)
(2)①当点P在AB边上时,在Rt△ABC中,∠B+∠C=90°,
在Rt△EDC中,∠DEC+∠C=90°, ∴∠DEC=∠B
∵DE⊥BC,∠PDQ=90° ∴∠PDQ=∠BDE=90° ∴∠BDP=∠EDQ
∴△BPD∽△EQD ……………………………………………………………(1分)
∴, 即,
∴ ………………………………………………………………………(1分)
∴CQ=EC-EQ……………………………………………………………(1分)
②当点P在AB的延长线上时,同理可得:,
∴CQ=EC+EQ …………………………………………………………(1分)
(3)∵线段PQ与线段DE的交点为点F,∴点P在边AB上
∵△BPD∽△EQD ∴
若设BP=x ,则, …………………………………(1分) 可得 ∴∠QPD=∠C
又可证∠PDE=∠CDQ ∴△PDF∽△CDQ
∵△PDF为等腰三角形 ∴△CDQ为等腰三角形………………………(1分)
①当CQ=CD时,可得: 解得:………………………(1分)
②当QC=QD时, 过点Q作QM⊥CB于M,
∴,
∴, 解得 ……………………………………………(1分)
③当DC=DQ时,过点D作DN⊥CQ于N,
∴,
∴, 解得(不合题意,舍去)…………………………(1分)
∴综上所述,或
8
(第6题)
(第9题)
(第10题)
(第13题)
A时
B时
A
B
C
B′
第15题图
C′
D
E
E′
F′
F
图①
图②
(第16题)
(第14题)
成绩分组 频数 频率
15≤x<18 3 0.03
18≤x<21 a 0.12
21≤x<24 20 0.20
24≤x<27 35 0.35
27≤x≤30 30 b
频数分布直方图:
频率分布表:
O
A
B
D
l
A
C
C
D
E
B
F
O
6cm
6. 5cm
8cm
A
B
C
6cm
6. 5cm
8cm
A
B
C
6cm
6. 5cm
8cm
A
B
C
A
B
E
C
D
A
B
C
E
D
第25题图
(备用图)
6cm
6cm
A
B
C
D
8cm
6cm
4cm
A
B
C
D
8cm
A
B
D
8cm
C
PAGE
7
同课章节目录
