函数单调性（５）[上学期]

课件39张PPT。§2.1.3 函数的简单性质
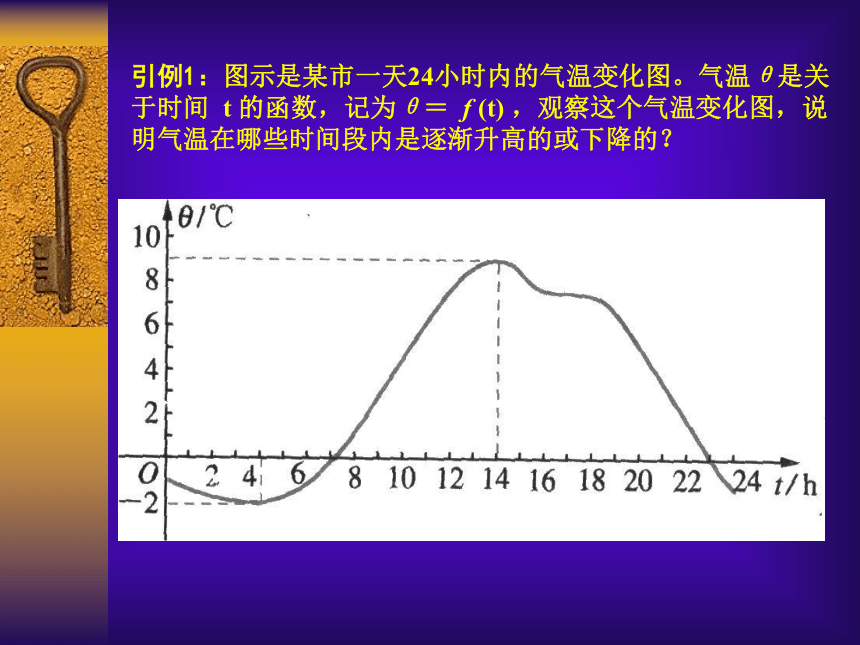
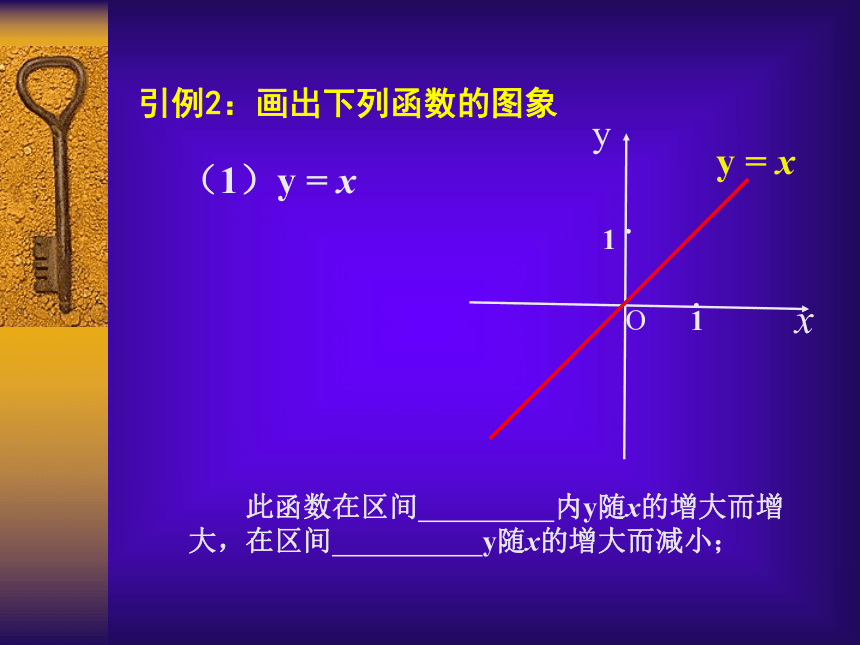
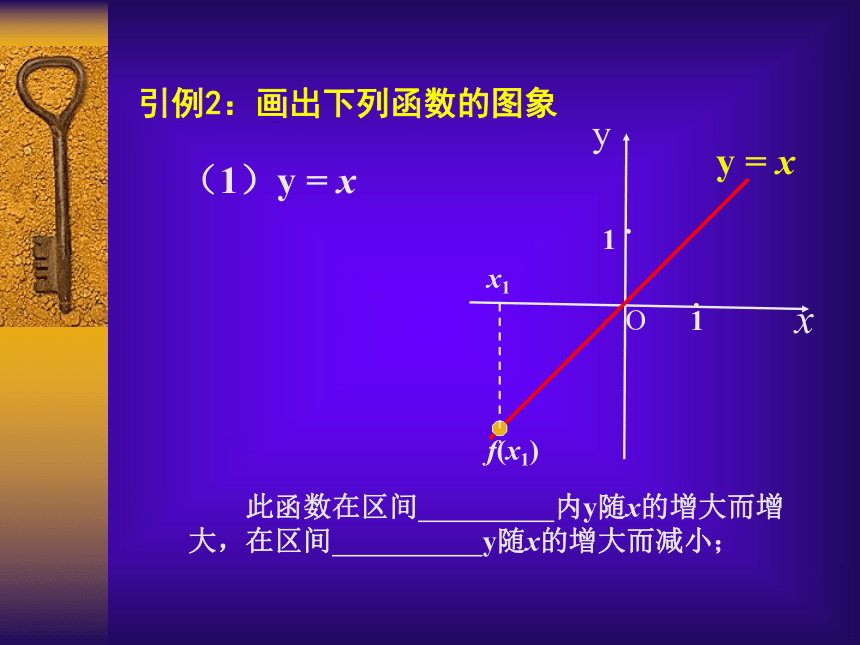
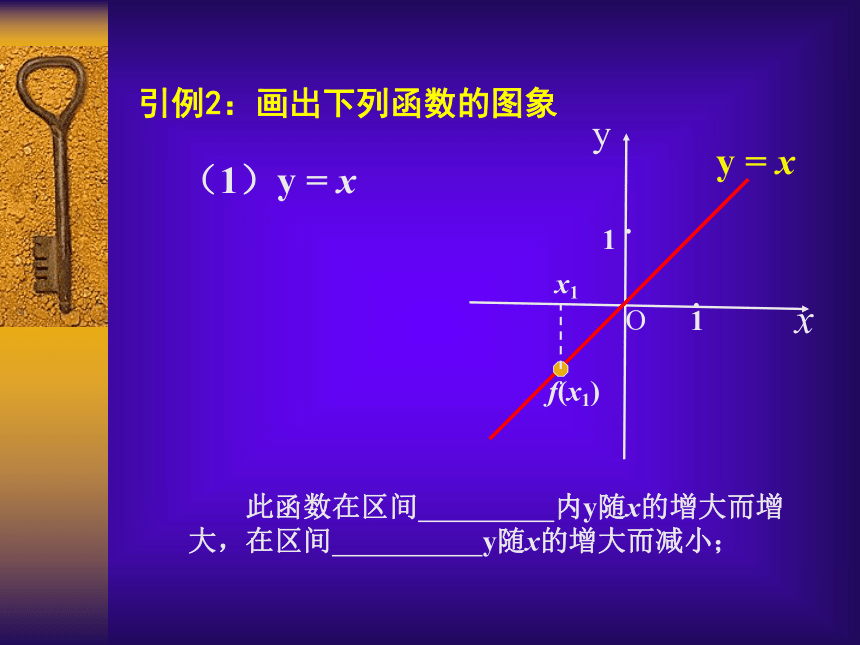
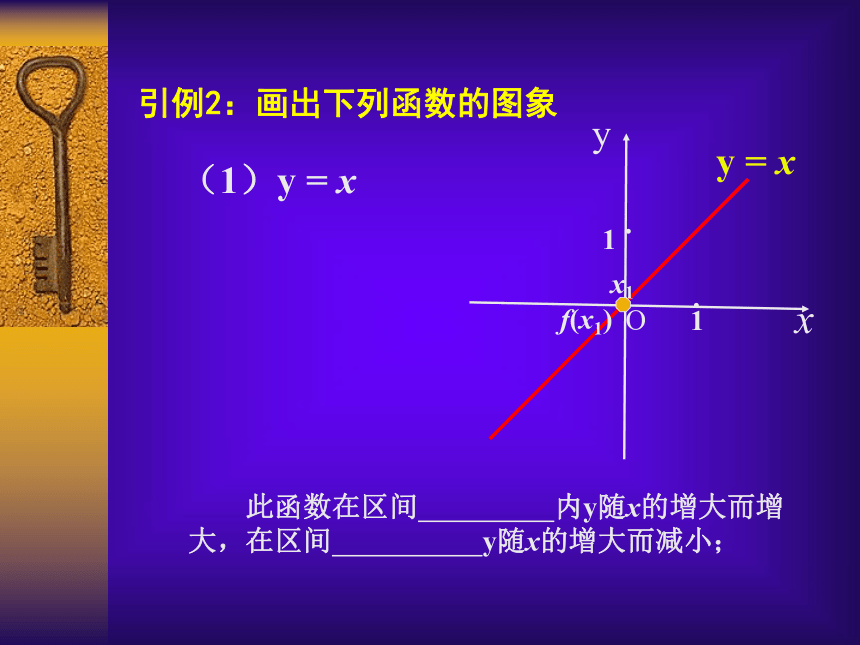
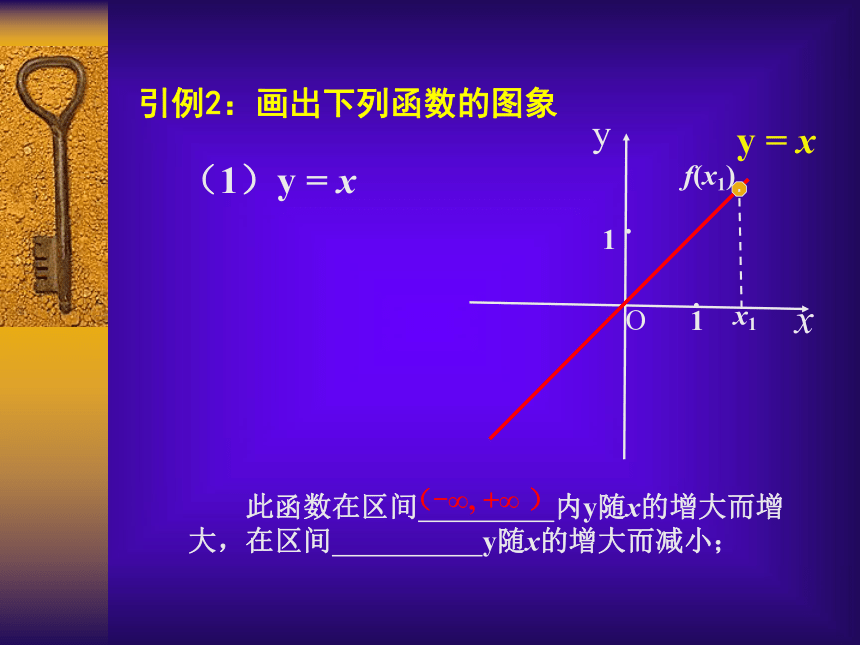
(函数的单调性)主讲人:吴江市青云中学 水菊芳引例1：图示是某市一天24小时内的气温变化图。气温θ是关于时间 t 的函数，记为θ＝ f (t) ，观察这个气温变化图，说明气温在哪些时间段内是逐渐升高的或下降的？ 引例2：画出下列函数的图象（1）y = xxyy = xO11··引例2：画出下列函数的图象（1）y = xxyy = xO11··引例2：画出下列函数的图象（1）y = x 此函数在区间 内y随x的增大而增大，在区间 y随x的增大而减小；xyy = xO11··引例2：画出下列函数的图象（1）y = x 此函数在区间 内y随x的增大而增大，在区间 y随x的增大而减小；x1f(x1)xyy = xO11··引例2：画出下列函数的图象（1）y = x 此函数在区间 内y随x的增大而增大，在区间 y随x的增大而减小；x1f(x1)xyy = xO11··引例2：画出下列函数的图象（1）y = x 此函数在区间 内y随x的增大而增大，在区间 y随x的增大而减小；x1f(x1)xyy = xO11··引例2：画出下列函数的图象（1）y = x 此函数在区间 内y随x的增大而增大，在区间 y随x的增大而减小；x1f(x1)xyy = xO11··引例2：画出下列函数的图象（1）y = x 此函数在区间 内y随x的增大而增大，在区间 y随x的增大而减小；x1f(x1)（-∞, +∞ ）（2）y = x2引例2：画出下列函数的图象Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1·Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。x1f(x1)Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。f(x1)x1Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。f(x1)x1Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。f(x1)x1Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。f(x1)x1Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。f(x1)x1Oxyy = x2（2）y = x2引例2：画出下列函数的图象1·1· 此函数在区间 内y随x的增大而增大，在区间 内y随x的增大而减小。f(x1)x1（-∞, 0 ][0, +∞ )0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····函数的单调性定义：函数的单调性定义： 设函数y= f (x)的定义域为A，区间I A函数的单调性定义： 设函数y= f (x)的定义域为A，区间I A如果对于区间I内的任意两个值x1，x2 ，
当x1< x2时，都有f(x1) < f(x2),
那么就说y= f (x) 在区间I上是增函数,
I称为y= f (x)单调增区间。函数的单调性定义： 设函数y= f (x)的定义域为A，区间I A如果对于区间I内的任意两个值x1，x2 ，
当x1< x2时，都有f(x1) < f(x2),
那么就说y= f (x) 在区间I上是增函数,
I称为y= f (x)单调增区间。如果对于区间I内的任意两个值x1，x2 ，
当x1< x2时，都有f(x1) > f(x2),那么
就说y= f (x)在区间I上是减函数,
I称为y= f (x)单调减区间。探索题 判断下列说法是否正确。2. 定义在R上的函数 f (x) 满足 f (-1) 函数的单调增区间为（0，2）；(×)(×)例1 求证：函数 f (x) = – – 1在区间（－∞，0）
上是单调增函数。1x例2 试判断函数y= x2 + x 在（0，＋∞）上是增函数还是减函数？并给予证明。解：函数y= x2 + x 在（0，＋∞）上是增函数下面给予证明：设 x1，x2 为区间(0,＋∞)上的任意两个值，且x1 = (x1 – x2) (x1 + x2) + (x1 – x2)
= (x1 – x2) (x1 + x2 +1)又 x2 ＞ x1 ＞ 0，所以x1 – x2< 0， x1 + x2 +1 ＞0，
所以f (x1)– f (x2)<0所以函数y= x2 + x 在（0，＋∞）上是增函数小结：在区间I内0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····判断函数单调性的方法：1、图象法 2、代数论证法证明函数的单调性常用步骤：(1)取值 (2)作差变形(3)定号 (4)结论思考题: 讨论函数y=x + (x ＞ 0)的单调性。1x作业：课本第37页
练习5、6谢谢，再见！