函数单调性(6)[上学期]

(共26张PPT)
江苏省通州高级中学
张春明
数与形,本是相倚依
焉能分作两边飞
数无形时少直觉
形少数时难入微
数形结合百般好
隔离分家万事休
切莫忘,几何代数统一体
永远联系莫分离
—— 华罗庚
赛季
得分
赛季
篮板
赛季
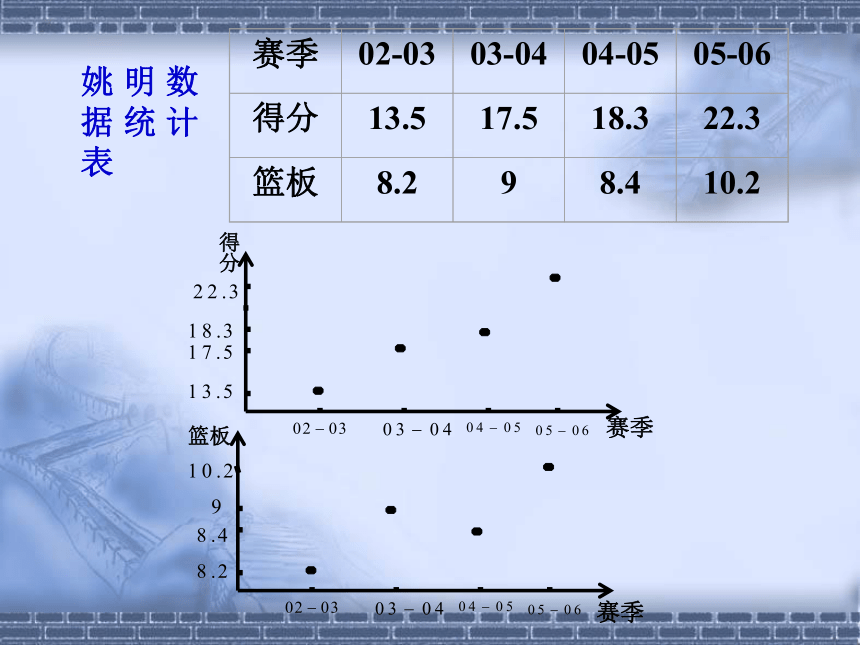
02-03
03-04
04-05
05-06
得分
13.5
17.5
18.3
22.3
篮板
8.2
9
8.4
10.2
姚明数据统计表
x
y
O
x
y
O
a
b
a
b
n
m
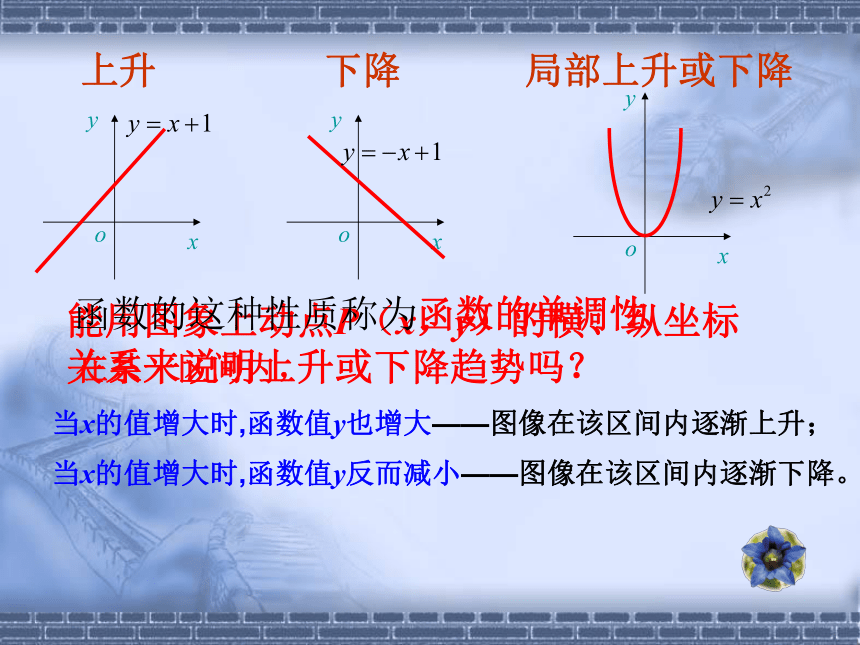
能用图象上动点P（x，y）的横、纵坐标关系来说明上升或下降趋势吗？
x
y
o
x
y
o
x
y
o
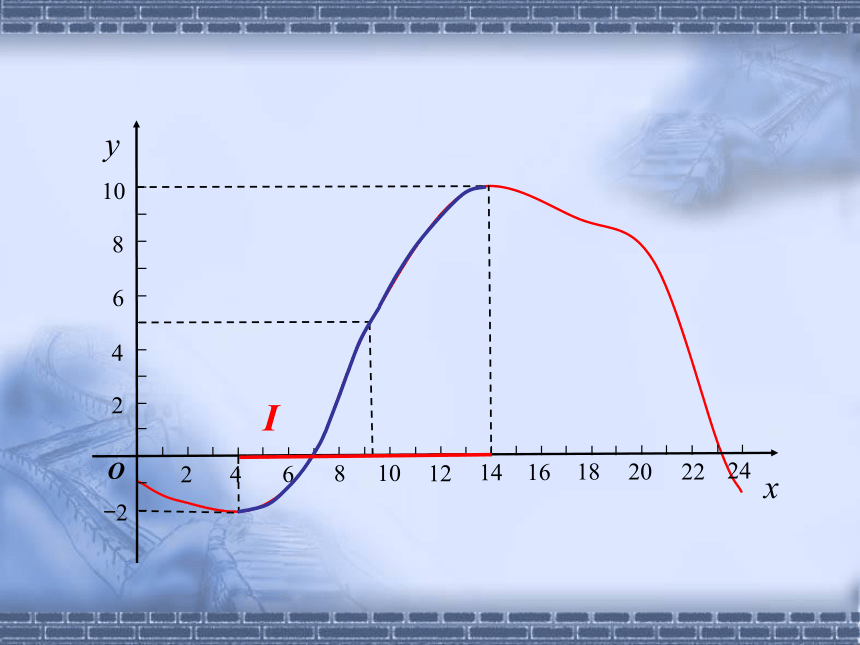
在某一区间内，
当x的值增大时,函数值y也增大——图像在该区间内逐渐上升；
当x的值增大时,函数值y反而减小——图像在该区间内逐渐下降。
函数的这种性质称为函数的单调性
局部上升或下降
下降
上升
y
2
4
6
8
10
O
-2
x
8
4
12
16
20
24
6
2
10
14
18
22
I
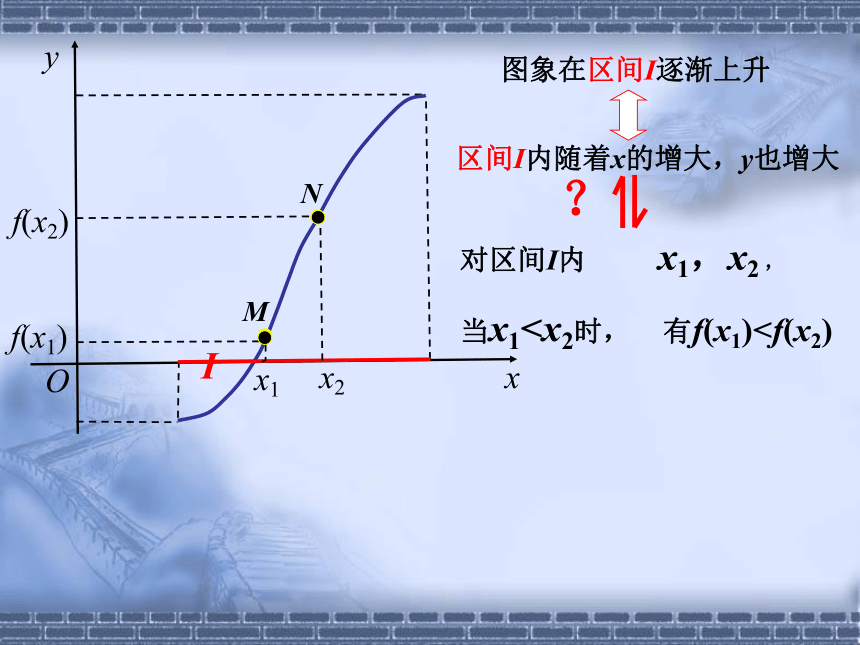
对区间I内 x1，x2 ，
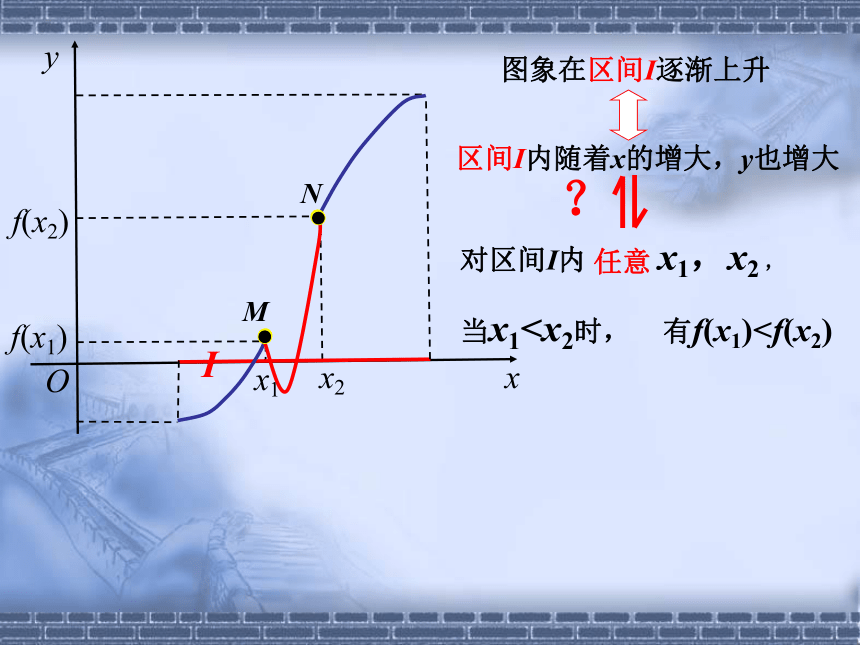
当x1图象在区间I逐渐上升
？
O
x
I
y
区间I内随着x的增大，y也增大
x1
x2
f(x1)
f(x2)
M
N
对区间I内 x1，x2 ，
当x1x
x1
x2
？
I
y
f(x1)
f(x2)
O
M
N
任意
区间I内随着x的增大，y也增大
图象在区间I逐渐上升
对区间I内 x1，x2 ，
当x1x
x1
x2
都
y
f(x1)
f(x2)
O
设函数y=f(x)的定义域为A,区间I A.
如果对于区间I上的任意
当x1<
定义
M
N
任意
两个自变量的值x1,x2，
I 称为 f (x)的单调
增区间.
那么就说 f (x)在区间I上
是单调增函数，
区间I内随着x的增大，y也增大
图象在区间I逐渐上升
I
那么就说在f(x)这个区间上是单调
减函数，I称为f(x)的单调 减 区间.
O
x
y
x1
x2
f(x1)
f(x2)
类比单调增函数的研究方法定义单调减函数.
x
O
y
x1
x2
f(x1)
f(x2)
设函数y=f(x)的定义域为A,区间I A.
如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2，
设函数y=f(x)的定义域为A,区间I A.
如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2，
那么就说在f(x)这个区间上是单调增 函数，I称为f(x)的单调 区间.
增
当x1<
当x1<
>
单调区间
（2）函数单调性是针对某个区间而言的，是一个局部性质;
（1）如果函数 y =f(x)在区间I是单调增函数或单调减函数，那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上，增函数的图象是上升的，减函数的图象是下降的。
判断1：函数 f (x)= x2 在 是单调增函数；
x
y
o
（2）函数单调性是针对某个区间而言的，是一个局部性质;
（1）如果函数 y =f(x)在区间I是单调增函数或单调减函数，那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上，增函数的图象是上升的，减函数的图象是下降的。
判断2：定义在R上的函数 f (x)满足 f (2)> f(1)，则函数 f (x)在R上是增函数；
（3） x 1, x 2 取值的任意性
y
x
O
1
2
f(1)
f(2)
例1、下图为函数 , 的图像，指出它的单调区间。
1
2
3
-2
-3
-2
-1
1
2
3
4
5
6
7
x
o
-4
-1
y
-1.5
[-1.5，3]，[5，6]
[-4，-1.5]，[3，5]，[6，7]
解：单调增区间为
单调减区间为
例2.画出下列函数图像，并写出单调区间：
x
y
_____________
,
讨论1：根据函数单调性的定义，
2试讨论　　　　　　　在　　　和　　　上的单调性？
？
变式2：讨论 的单调性
成果交流
变式1：讨论 的单调性
x
y
y=-x2+2
1
-1
1
2
2
-1
-2
-2
_______;
_______.
例2.画出下列函数图像，并写出单调区间：
例3.判断函数 在定义域 上的单调性.
（教材P43/7(4))
描点作图
1. 任取x1，x2∈D，且x12. 作差f(x1)－f(x2)；
3. 变形（通常是因式分解和配方）；
4. 定号（即判断差f(x1)－f(x2)的正负）；
5. 下结论
主要步骤
并给出证明
试用定义法证明函数 　
在区间 上是单调增函数。
小结
1.函数单调性的定义中有哪些关键点？
2.判断函数单调性有哪些常用方法？
3.你学会了哪些数学思想方法？
作业
2、证明函数 f（x）=-x2在 上是 减函数。
3、证明函数 f（x）= 在 上是单调递增的。(选做)
1、教材 p37 /5，6，7
数与形,本是相倚依,
焉能分作两边飞;
数无形时少直觉,
形少数时难入微;
数形结合百般好,
隔离分家万事休;
切莫忘,几何代数统一体,
永远联系莫分离.
——华罗庚
单调增区间
单调减区间
a>0
a<0
的对称轴为
返回
证明：在区间 上任取两个值 且
则
，且
所以函数 在区间上 是增函数.
取值
作差
变形
定号
结论
返回
返回
是定义在R上的单调函数，且 的图
象过点A（0，2）和B（3，0）
（1）解方程
（2）解不等式
（3）求适合 的 的取值范围
成果运用
若二次函数 的单调增区间是 ， 则a的取值情况是 （ ）
变式1
变式2
请你说出一个单调减区间是 的二次函数
变式3
请你说出一个在 上单调递减的函数
若二次函数 在区间 上单调递增，求a的取值范围。
A. B. C. D.
________
成果运用
若二次函数 在区间 上单调递增，求a的取值范围。
解：二次函数 的对称轴为 ,
由图象可知只要 ，即 即可.
o
x
y
1
x
y
1
o