函数奇偶性[上学期]
图片预览





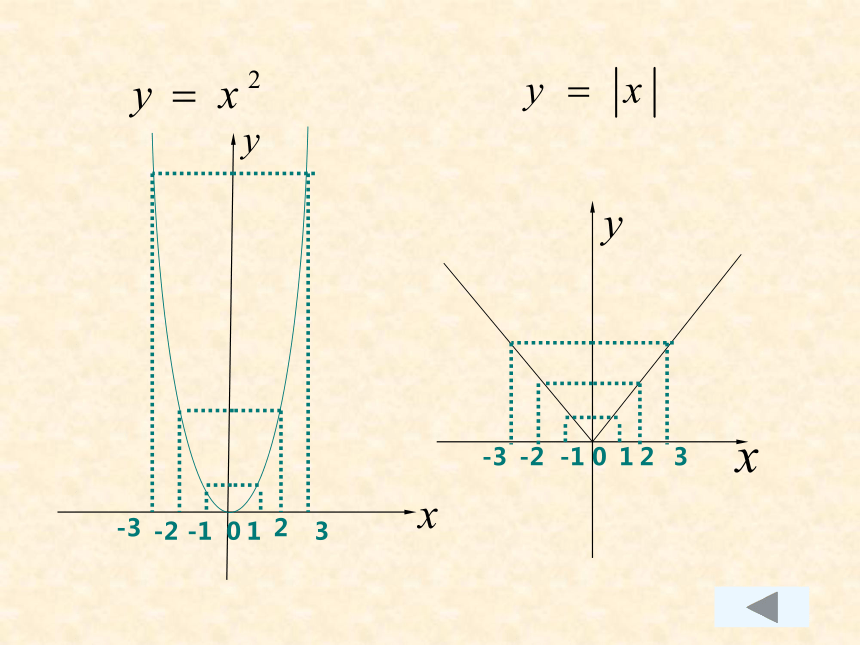





文档简介
课件30张PPT。高中数学必修1 2.1.3 函数的奇偶性(上课) 宝安高级中学 柯祖安 一. 实图引入,激发学习兴趣: 观察下列图片,感受其对称美:我们刚学习的函数的单调性是从函数图象的什么特征来研究的?以上几幅图象,它们具有怎样的对称性?你学过的函数中有哪些函数具有这样的图象特征? 1
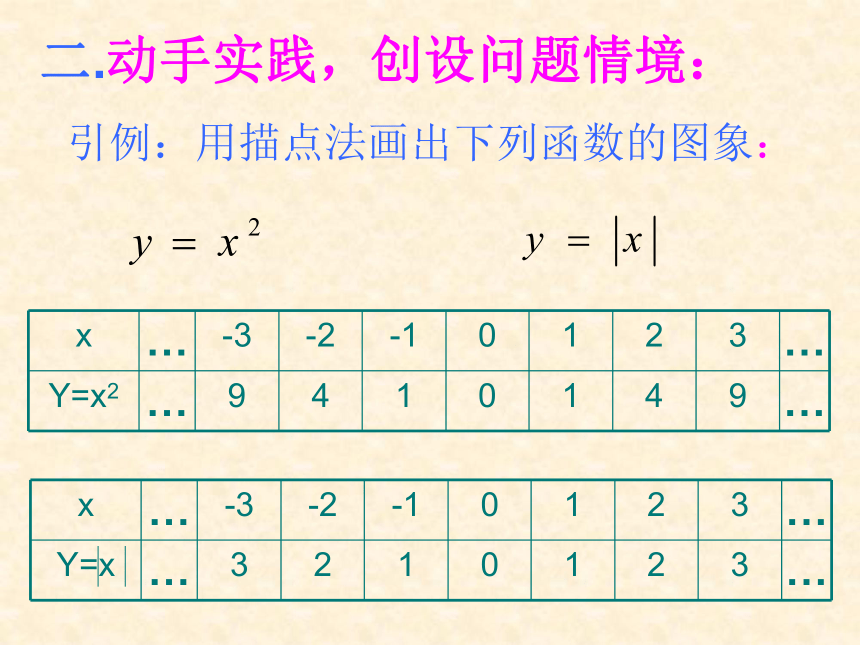
二.动手实践,创设问题情境: 引例:用描点法画出下列函数的图象: 21-13-2-3023-30-1-21【问题1】观察图象,从对称的角度看,它们有什么共同特征?【问题2】你还能举出几个图象关于y轴对称的函数吗?都是以y轴为对称轴的轴对称图形 比如,函数 , 象这样,图象关于y轴对称的函数
称为偶函数。【问题3】你能由图象判断下列函数是否为偶函数吗?(1)(2)(3)(4)三.归纳抽象,自主建构数学: 数缺形少直观、形缺数不入微。
----华罗庚类比函数单调性的判断,可从“形”和“数”两个方面进行,那么:
偶函数图象(关于y轴对称)的这种对称性除了可以从图象上认识外,还可以从数量关系上如何表述? 【问题4】请分析前面引例中的描点作图过程,说说函数 的图象为什么关于y轴对称呢?〖1〗因为描的点是对称点,如:
点(1,1)和(-1,1),(2,4)和(-2,4),(3,9)和(-3,9)等等。〖2〗因为取任意的实数a和取它的相反数-a,得到的值相等。即f(-a)=f(a)=a2,而点(a,a2)和(-a,a2)是关于y轴对称的,所以整个图象就关于y轴对称。【问题5】根据a值的任意性,对于函数y=x2中任意给定的一个实数x值,是否都满足f(-x)=f(x)呢?满足,因为f(-x)=f(x)=x2 【问题8】反过来,满足f(-x)=f(x)的函数f(x),其图象一定关于y轴对称吗?一定是,因为对函数定义域内任意给定的一个a值,都有f(-a)=f(a),即图象上有点(a,f(a))和(-a,f(a)),而它们又是关于y轴对称的点,所以整个函数图象就会关于y轴对称。 【问题7】我们能否说:如果函数f(x)的图象关于y轴对称,那么有f(-x)=f(x)呢?【问题9】怎样从数的角度给“偶函数”下个定义呢?如果对于函数y=f(x)的定义域内的任意一个x值,都有f(-x)=f(x),那么称函数y=f(x)是偶函数。
显然,偶函数的图象关于y轴对称。提问:判断【问题3】中的函数(3) ;(4)
是否为偶函数?请看几何画板展示图象,直观验证。四.类比学习,合作探究新知: 以上我们研究的是偶函数,其图象是关于y轴对称的的轴对称图象。那么,是否有关于原点成中心对称的函数图象呢?这样的函数又满足怎样的数量关系呢?为什么呢?请以函数 , 为例,类比建构“偶函数”概念的过程,描点画图,找图象特征,分析数量关系,归纳结论.21-13-2-3023-30-1-21f(-1)= - f(1)f(-2)= - f(2)f(-3)= - f(3)……f(-x)=f(-a)=- f(a)- f(x)如果对于函数y=f(x)的定义域内的任意一个x值,都有f(-x)= - f(x),那么称函数y=f(x)是奇函数。
显然,奇函数的图象关于原点对称。如果函数是奇函数或偶函数,我们就说函数具有奇偶性。五.数学运用,练习巩固概念: 对于(4),问:用“特值法”去检验
是否对于函数定义域内的任意一个 值都成立?【例2】判断下列函数是否具有奇偶性:问:
上面例1中的四个函数你还能用什么方法判断奇偶性?
这个方法用于例2的判断,合适吗?【演练反馈】判断下列函数是否具有奇偶性:(1)(2)(3)(4)六.对比生疑,再探概念内涵: 【问题10】函数 是偶函数,
函数 也是偶函数,
那么,函数 还是偶函数吗?为什么? 〖1〗不是,因为函数的图象不关于y轴对称。〖2〗不是,因为定义域不关于数“0”对称。七.猜想预言,发展思维能力: 1、按照奇偶性判断,以上例题中呈现出了三种函数类型:奇非偶、偶非奇、非奇非偶。请你猜想:是否存在既是奇函数又是偶函数的函数?其图象有何特征?解析式如何?
2、你能预言:奇(偶)函数的图象特征对我们研究函数的作图以及判断函数的单调性有何数学价值吗?小结:
1、既奇且偶的函数,如:
2、奇(偶)函数的图象特征用于(1)简化函数作图---只要作出x>0的部分,由对称性可以作出x<0的部分。
(2)简化函数性质的研究---如在x>0是增函数,那么在x<0就一定是减函数。 八.小结提炼,回顾反思作业: 【归纳】
函数的奇偶性体现的是一种对称性质:
①奇(偶)函数满足 或 ;
②定义域关于数“0”对称是函数有奇偶性的必要条件;
③一个函数的奇偶性可能是非奇非偶或既奇又偶;
④奇函数在y轴两侧的对称区间单调性相同、偶函数在y轴两侧的对称区间单调性相反。 【作业】
1、判断下列函数的奇偶性:2、证明函数 ,当n为奇数时是奇函数;当n为偶数时是偶函数.3、若函数 是偶函数,求实数 的值.▲对于基础好的学生,可以做:
《课课练》P21页1、3、7、8题
P22页1、2、4题谢 谢 大 家!
二.动手实践,创设问题情境: 引例:用描点法画出下列函数的图象: 21-13-2-3023-30-1-21【问题1】观察图象,从对称的角度看,它们有什么共同特征?【问题2】你还能举出几个图象关于y轴对称的函数吗?都是以y轴为对称轴的轴对称图形 比如,函数 , 象这样,图象关于y轴对称的函数
称为偶函数。【问题3】你能由图象判断下列函数是否为偶函数吗?(1)(2)(3)(4)三.归纳抽象,自主建构数学: 数缺形少直观、形缺数不入微。
----华罗庚类比函数单调性的判断,可从“形”和“数”两个方面进行,那么:
偶函数图象(关于y轴对称)的这种对称性除了可以从图象上认识外,还可以从数量关系上如何表述? 【问题4】请分析前面引例中的描点作图过程,说说函数 的图象为什么关于y轴对称呢?〖1〗因为描的点是对称点,如:
点(1,1)和(-1,1),(2,4)和(-2,4),(3,9)和(-3,9)等等。〖2〗因为取任意的实数a和取它的相反数-a,得到的值相等。即f(-a)=f(a)=a2,而点(a,a2)和(-a,a2)是关于y轴对称的,所以整个图象就关于y轴对称。【问题5】根据a值的任意性,对于函数y=x2中任意给定的一个实数x值,是否都满足f(-x)=f(x)呢?满足,因为f(-x)=f(x)=x2 【问题8】反过来,满足f(-x)=f(x)的函数f(x),其图象一定关于y轴对称吗?一定是,因为对函数定义域内任意给定的一个a值,都有f(-a)=f(a),即图象上有点(a,f(a))和(-a,f(a)),而它们又是关于y轴对称的点,所以整个函数图象就会关于y轴对称。 【问题7】我们能否说:如果函数f(x)的图象关于y轴对称,那么有f(-x)=f(x)呢?【问题9】怎样从数的角度给“偶函数”下个定义呢?如果对于函数y=f(x)的定义域内的任意一个x值,都有f(-x)=f(x),那么称函数y=f(x)是偶函数。
显然,偶函数的图象关于y轴对称。提问:判断【问题3】中的函数(3) ;(4)
是否为偶函数?请看几何画板展示图象,直观验证。四.类比学习,合作探究新知: 以上我们研究的是偶函数,其图象是关于y轴对称的的轴对称图象。那么,是否有关于原点成中心对称的函数图象呢?这样的函数又满足怎样的数量关系呢?为什么呢?请以函数 , 为例,类比建构“偶函数”概念的过程,描点画图,找图象特征,分析数量关系,归纳结论.21-13-2-3023-30-1-21f(-1)= - f(1)f(-2)= - f(2)f(-3)= - f(3)……f(-x)=f(-a)=- f(a)- f(x)如果对于函数y=f(x)的定义域内的任意一个x值,都有f(-x)= - f(x),那么称函数y=f(x)是奇函数。
显然,奇函数的图象关于原点对称。如果函数是奇函数或偶函数,我们就说函数具有奇偶性。五.数学运用,练习巩固概念: 对于(4),问:用“特值法”去检验
是否对于函数定义域内的任意一个 值都成立?【例2】判断下列函数是否具有奇偶性:问:
上面例1中的四个函数你还能用什么方法判断奇偶性?
这个方法用于例2的判断,合适吗?【演练反馈】判断下列函数是否具有奇偶性:(1)(2)(3)(4)六.对比生疑,再探概念内涵: 【问题10】函数 是偶函数,
函数 也是偶函数,
那么,函数 还是偶函数吗?为什么? 〖1〗不是,因为函数的图象不关于y轴对称。〖2〗不是,因为定义域不关于数“0”对称。七.猜想预言,发展思维能力: 1、按照奇偶性判断,以上例题中呈现出了三种函数类型:奇非偶、偶非奇、非奇非偶。请你猜想:是否存在既是奇函数又是偶函数的函数?其图象有何特征?解析式如何?
2、你能预言:奇(偶)函数的图象特征对我们研究函数的作图以及判断函数的单调性有何数学价值吗?小结:
1、既奇且偶的函数,如:
2、奇(偶)函数的图象特征用于(1)简化函数作图---只要作出x>0的部分,由对称性可以作出x<0的部分。
(2)简化函数性质的研究---如在x>0是增函数,那么在x<0就一定是减函数。 八.小结提炼,回顾反思作业: 【归纳】
函数的奇偶性体现的是一种对称性质:
①奇(偶)函数满足 或 ;
②定义域关于数“0”对称是函数有奇偶性的必要条件;
③一个函数的奇偶性可能是非奇非偶或既奇又偶;
④奇函数在y轴两侧的对称区间单调性相同、偶函数在y轴两侧的对称区间单调性相反。 【作业】
1、判断下列函数的奇偶性:2、证明函数 ,当n为奇数时是奇函数;当n为偶数时是偶函数.3、若函数 是偶函数,求实数 的值.▲对于基础好的学生,可以做:
《课课练》P21页1、3、7、8题
P22页1、2、4题谢 谢 大 家!
