函数的单调性[上学期]
图片预览


文档简介
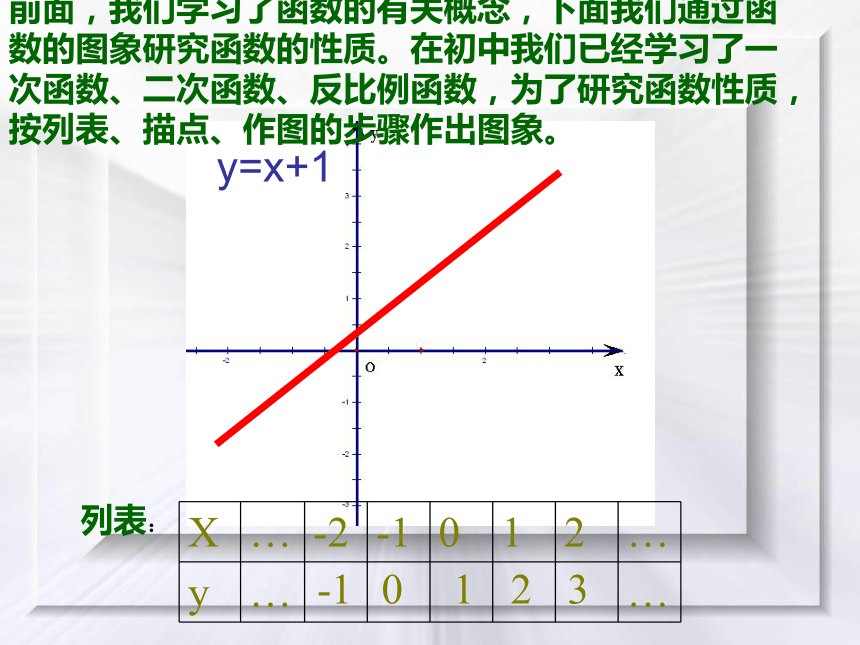
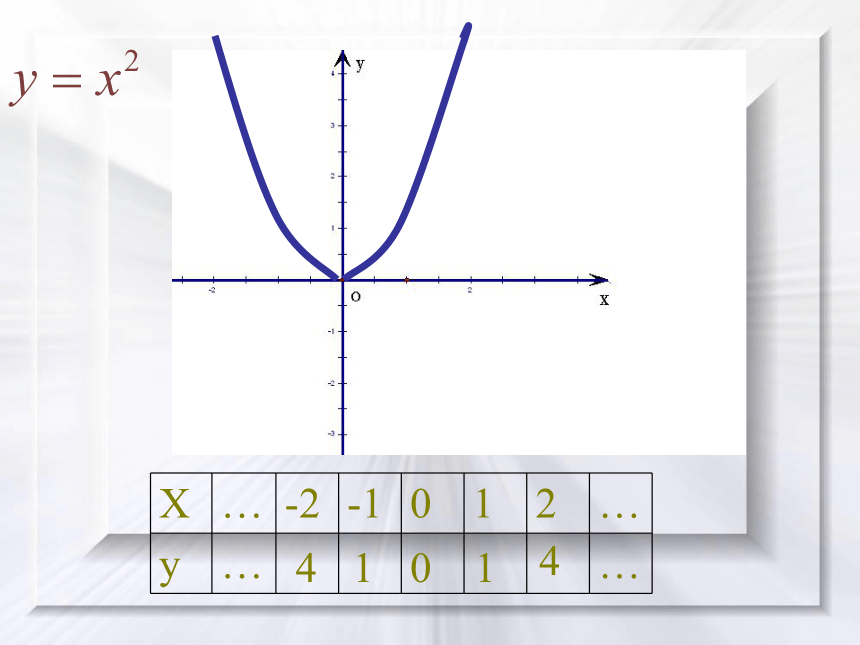
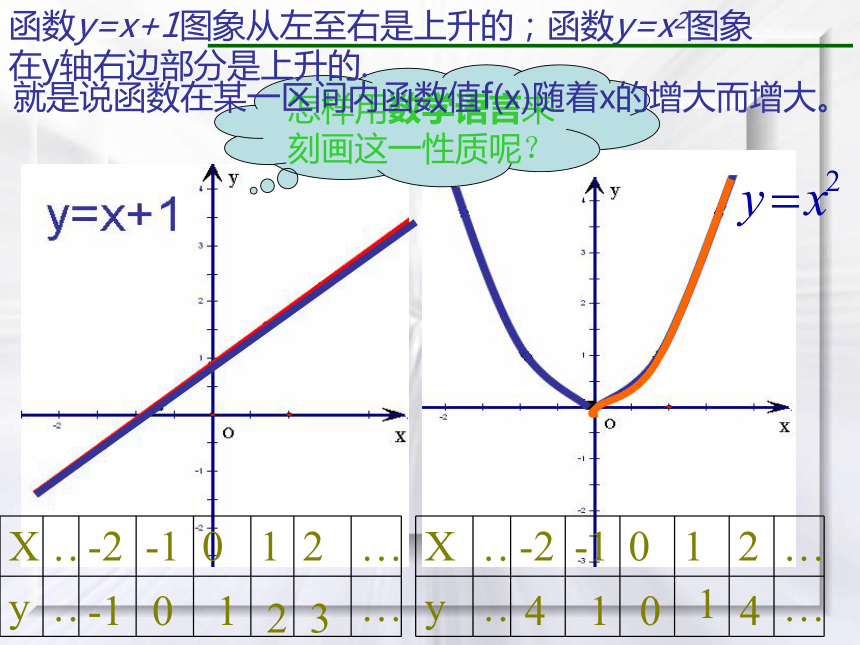
课件16张PPT。2.1.3 函数的单调性y=x+1前面,我们学习了函数的有关概念,下面我们通过函数的图象研究函数的性质。在初中我们已经学习了一次函数、二次函数、反比例函数,为了研究函数性质,按列表、描点、作图的步骤作出图象。-10123列表:14014怎样用数学语言来刻画这一性质呢?14014-10123函数y=x+1图象从左至右是上升的;函数y=x2图象
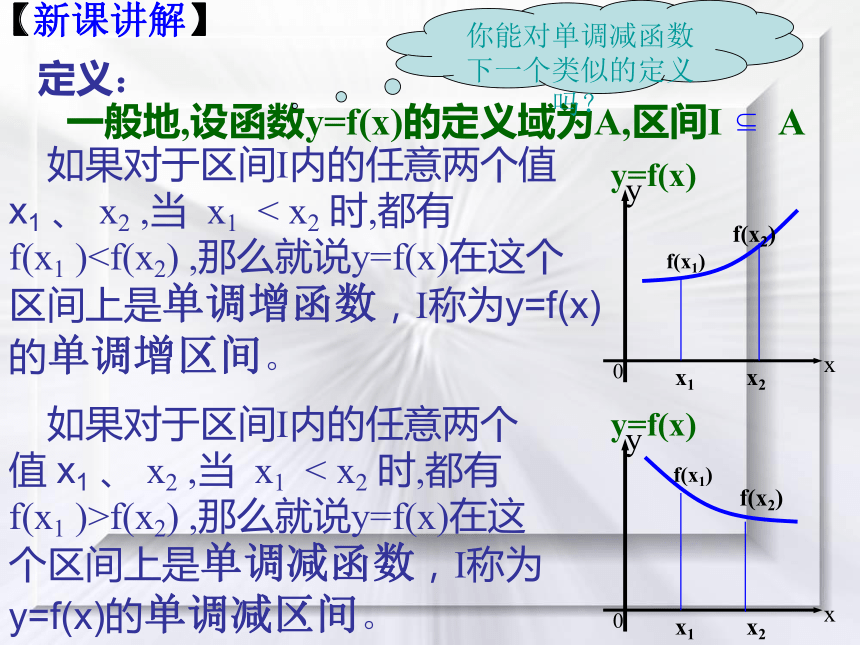
在y轴右边部分是上升的.就是说函数在某一区间内函数值f(x)随着x的增大而增大。定义: 如果对于区间I内的任意两个值 x1 、 x2 ,当 x1 < x2 时,都有f(x1 )【新课讲解】定义: 如果对于区间I内的任意两个值 x1 、 x2 ,当 x1 < x2 时,都有f(x1 )你能对单调减函数下一个类似的定义吗?【新课讲解】 如果对于区间I内的任意两个值 x1 、 x2 ,当 x1 < x2 时,都有f(x1 )>f(x2) ,那么就说y=f(x)在这个区间上是单调减函数,I称为y=f(x)的单调减区间。函数 在定义域R上具有单调性吗?
函数的单调性是对定义域内某个区间而言,
它反映的是函数的局部性质.函数在某个区间
上是单调增(减)函数,但是在整个定义域上不
一定是单调函数.问:
函数在(-∞,0)是单调____函数。
在(0,+∞)是单调____函数。减减那么,能否说函数在(-∞,0)∪ (0,+∞)是单调减函数吗?从图象上看,从左到右,函数值f(x)随着 x值增大而一直在减小吗?从定义上看,单调减函数:x1 < x2 x1= -1, x2 =1<多个单调增(减)区间一般不用“∪”连接!例1 如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间(包括端点) ,以及在每一单调区间上,函数y=f(x)是增函数还是减函数. 解:函数f(x)的单调区间有:_______________________其中在区间_____________上是增函数,
在区间_______________上是减函数.【例题】[-5,-2]、[-2,1]、[1,3]、[3,5]
[-5,-2 ] ,[1,3 ][-2,1 ] ,[3,5]例2 证明函数 在R上是增函数.证明:设 x1 ,x2 是R上的任意两个实数
且 ,则在R上是增函数. 【小结与归纳】 用定义证明函数单调性的一般步骤是: ⑵比较 的大小 ⑴设 是给定区间内的任意两个值,且(3)根据 的大小关系确定其单调性例3 证明函数 在(- ∞,0 )上是单调增函数.证明:设 是 上的任意两个实数,
且 ,则所以,函数 在(- ∞,0 )上是单调增函数.【练习】1. 说出已知函数图象的单调区间(包括端点)。2.证明f (x)= - x2-4x+3在(-∞,-2]上为增函数其中在区间_____________上是减函数,
在区间_______________上是增函数.解:函数f(x)的单调区间有:_______________________[-2,-1]、[-1,0]、[0,1]、[1,2]
[-2,-1 ] ,[0,1][-1,0 ] ,[1,2]1.单调性是对某个区间而言的,并且单调区间一定是定义域的一个子集,单调区间一般不能以并集的形式出现.2.判断函数的单调性:一、根据图象判断;二、利用单调性的定义证明.本节课我们学习了函数单调性,【 小结】【 作业】教材P37 练习 1、2 、6对于一般二次函数y=ax2+bx+c(a≠0), 你能判断它的单调区间,给出相应的证明吗?
在y轴右边部分是上升的.就是说函数在某一区间内函数值f(x)随着x的增大而增大。定义: 如果对于区间I内的任意两个值 x1 、 x2 ,当 x1 < x2 时,都有f(x1 )
函数的单调性是对定义域内某个区间而言,
它反映的是函数的局部性质.函数在某个区间
上是单调增(减)函数,但是在整个定义域上不
一定是单调函数.问:
函数在(-∞,0)是单调____函数。
在(0,+∞)是单调____函数。减减那么,能否说函数在(-∞,0)∪ (0,+∞)是单调减函数吗?从图象上看,从左到右,函数值f(x)随着 x值增大而一直在减小吗?从定义上看,单调减函数:x1 < x2 x1= -1, x2 =1<多个单调增(减)区间一般不用“∪”连接!例1 如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间(包括端点) ,以及在每一单调区间上,函数y=f(x)是增函数还是减函数. 解:函数f(x)的单调区间有:_______________________其中在区间_____________上是增函数,
在区间_______________上是减函数.【例题】[-5,-2]、[-2,1]、[1,3]、[3,5]
[-5,-2 ] ,[1,3 ][-2,1 ] ,[3,5]例2 证明函数 在R上是增函数.证明:设 x1 ,x2 是R上的任意两个实数
且 ,则在R上是增函数. 【小结与归纳】 用定义证明函数单调性的一般步骤是: ⑵比较 的大小 ⑴设 是给定区间内的任意两个值,且(3)根据 的大小关系确定其单调性例3 证明函数 在(- ∞,0 )上是单调增函数.证明:设 是 上的任意两个实数,
且 ,则所以,函数 在(- ∞,0 )上是单调增函数.【练习】1. 说出已知函数图象的单调区间(包括端点)。2.证明f (x)= - x2-4x+3在(-∞,-2]上为增函数其中在区间_____________上是减函数,
在区间_______________上是增函数.解:函数f(x)的单调区间有:_______________________[-2,-1]、[-1,0]、[0,1]、[1,2]
[-2,-1 ] ,[0,1][-1,0 ] ,[1,2]1.单调性是对某个区间而言的,并且单调区间一定是定义域的一个子集,单调区间一般不能以并集的形式出现.2.判断函数的单调性:一、根据图象判断;二、利用单调性的定义证明.本节课我们学习了函数单调性,【 小结】【 作业】教材P37 练习 1、2 、6对于一般二次函数y=ax2+bx+c(a≠0), 你能判断它的单调区间,给出相应的证明吗?
