函数的奇偶性[上学期]
图片预览






文档简介
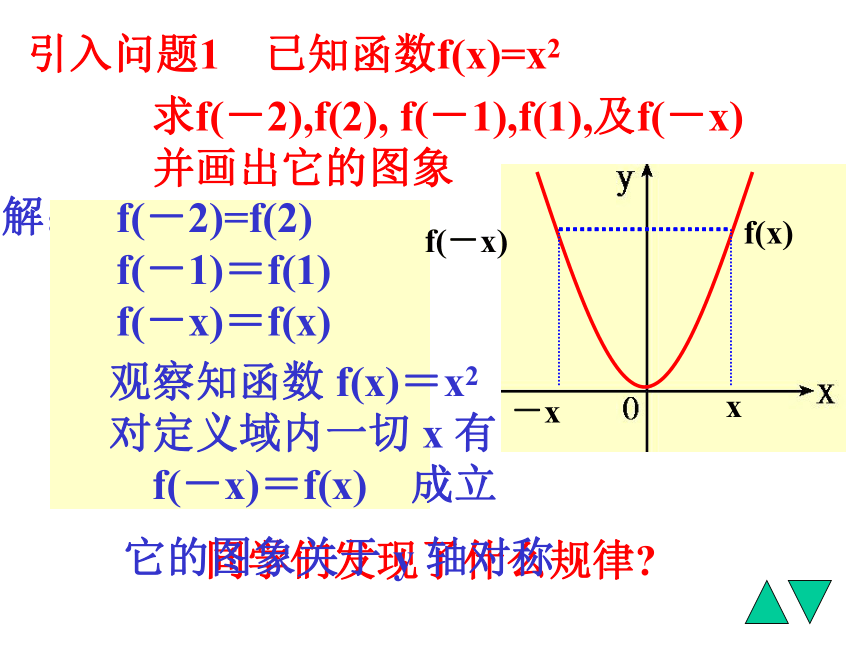
课件21张PPT。请安静函数的奇偶性引入问题1 已知函数f(x)=x2求f(-2),f(2), f(-1),f(1),及f(-x)
并画出它的图象解:f(-2)=(-2)2=4f(-1)=(-1)2=1f(2)=4f(1)=1f(-x)=(-x)2=x 2同学们发现了什么规律?f(-2)=f(2)
f(-1)=f(1)
f(-x)=f(x)x-xf(x)f(-x)观察知函数 f(x)=x2
对定义域内一切 x 有
f(-x)=f(x) 成立它的图象关于 y 轴对称偶函数定义: 如果对于f(x)定义域内的任意一个x, 都有
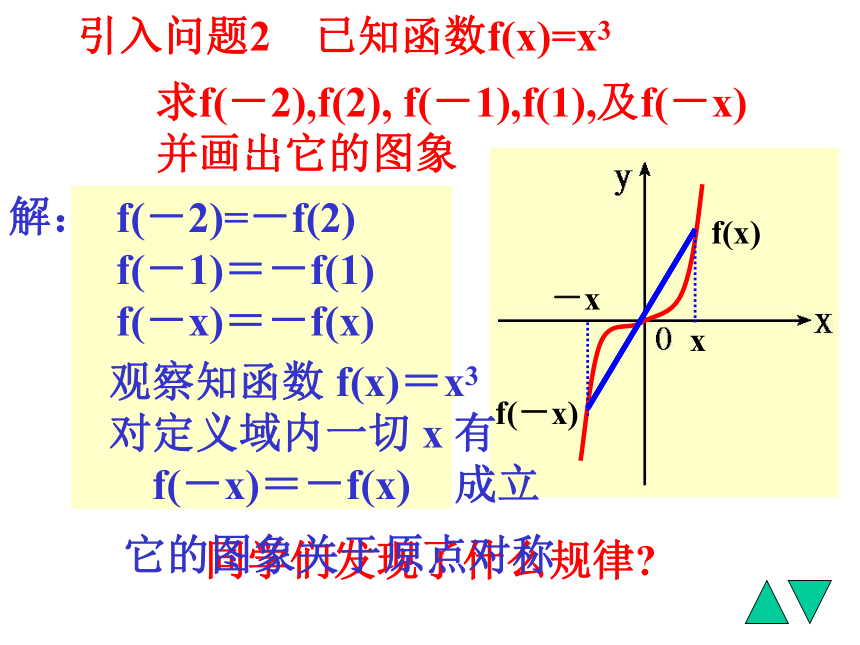
f(-x)=f(x), 那么函数f(x)就叫偶函数.前面讨论的函数 f(x)=x2 按定义是偶函数函数 f(x)=x4 是偶函数吗?函数 f(x)=x10 是偶函数吗?函数 f(x)=x2n n∈Z 是偶函数吗?函数 f(x)=x2n n∈Z 一定是偶函数 引入问题2 已知函数f(x)=x3求f(-2),f(2), f(-1),f(1),及f(-x)
并画出它的图象解:f(-2)=(-2)3=-8 f(2)=22=8 f(-1)=(-1)3=-1 f(1)=13=1 f(-x)=(-x)3=-x 3同学们发现了什么规律?f(-2)=-f(2)
f(-1)=-f(1)
f(-x)=-f(x)xf(x)-xf(-x)观察知函数 f(x)=x3
对定义域内一切 x 有
f(-x)=-f(x) 成立它的图象关于原点对称奇函数定义:如果对于f(x)定义域内的任意一个x, 都有
f(-x)=-f(x), 那么函数f(x)就叫奇函数.前面讨论的函数 f(x)=x3 按定义是奇函数函数 f(x)=x5 是奇函数吗?函数 f(x)=x13 是奇函数吗?函数 f(x)=x2n-1 n∈Z 是奇函数吗?函数 f(x)=x2n-1 n∈Z 一定是奇函数 如果一个函数f(x)是奇函数或偶函数,
那么我们就说函数 f(x) 具有奇偶性。探究:具有奇偶性的函数,其定义域具有怎样的特点?具有奇偶性的函数,其定义域关于数“0”对称对奇函数、偶函数定义的说明:(1)定义域关于原点对称是函数具有奇偶性
的前提条件Oab-a-b(2)奇、偶函数定义的逆命题也成立,即:
若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数
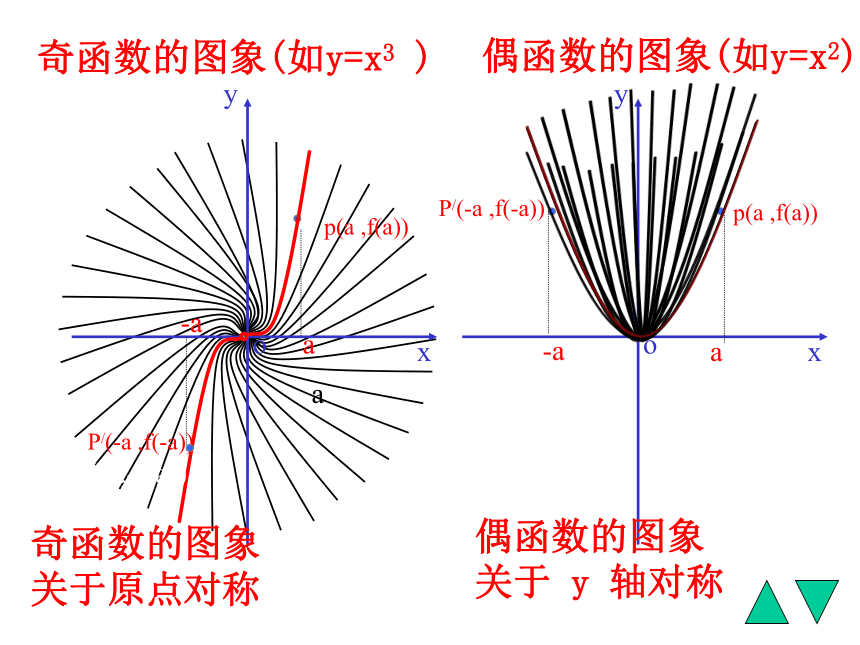
那么我们就说函数 f(x) 具有奇偶性。奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))奇函数的图象
关于原点对称偶函数的图象
关于 y 轴对称练习1. 说出下列函数的奇偶性:偶函数奇函数①f(x)=x4 ________ ④ f(x)= x -1 ________② f(x)=x ________⑤f(x)=x -2 __________③ f(x)=x5 __________⑥f(x)=x -3 ________ 说明:对于形如 f(x)=x n 的函数,
若n为偶数,则它为偶函数。
若n为奇数,则它为奇函数。奇函数奇函数奇函数偶函数例1 已知函数y=f(x)是偶函数,它在y轴右边 的图象如图,画出它在 y 轴左边的图象oyx解:画法略 y x 0例2 判断函数 f(x)=x3+2x 的奇偶性解:函数的定义域是 R ∵ f(-x)=(-x)3+2(-x)=-x 3 -2x=-f(x)∴ f(x) 是奇函数=-(x 3+2x)研究函数的奇偶性
必须首先讨论函数的定义域
仅当函数的定义域关于原点对称
才能说它具有奇偶性例3 判断函数 f(x)=2x4+3x2 的奇偶性解:函数的定义域是 R ∵ f(-x)=2(-x)4+3(-x)2=2x4 +3x2=f(x)∴ f(x) 是偶函数研究函数的奇偶性
必须首先讨论函数的定义域
仅当函数的定义域关于原点对称
才能说它具有奇偶性例4判断函数 f(x)=5 的奇偶性解:函数的定义域是 R ∵ f(-x)=5=f(x),且 f(-x)≠-f(x)∴ f(x) 是偶函数不是奇函数判断函数 f(x)=0 的奇偶性 ∵ f(-x)=0=f(x) 且 -f(x)=0=f(-x) ∴ f(x) 既是奇函数又是偶函数说明:定义域关于原点对称的函数
若是非零的常数函数是偶函数
在定义域内恒等于零的函数
既是奇函数又是偶函数例5 判断函数 f(x)=x+1 的奇偶性解:函数的定义域是 R ∵ f(-x)=(-x)+1=-x+1 ∴ f(-x)≠f(x) ∵ -f(x)=-(x+1)=-x-1 ∴ f(-x)≠-f(x) 因此,f(x) 是非奇非偶函数另解:由图象知,不具有对称性 由此可知 f(x) 是非奇非偶函数例6 判断函数 f(x)=x2 x∈[-1,3] 的奇偶性解:∵ 函数的定义域是 [-1,3]不是关于原点对称∴ f(x) 是非奇非偶函数另解:∵ 图象不具有对称性 ∴ f(x) 是非奇非偶函数说明:根据奇偶性, 函数可划分为四类:奇函数-它的图象关于原点对称偶函数-它的图象关于 y 轴对称既奇又偶函数-在定义域内恒为零非奇非偶函数-图象不具有对称性课堂练习判断下列函数的奇偶性(不写证明过程)1 f(x)=x4-3x2+52 f(x)=x5-3x3+5x3 f(x)=x5-3/x3+54 f(x)=x+1/x5 f(x)=(x4-1)/x2偶函数偶函数奇函数奇函数非奇非偶函数思考题:1﹑函数f(x)是定义在R上的偶函数,
如果f(x)在x∈[0,+∞)上是单调增函数,那么f(x)在x∈(-∞,0)上是单调 函数。减2﹑函数f(x)是定义在R上的奇函数,
如果f(x)在x∈[0,+∞)上是单调增函数,那么f(x)在x∈(-∞,0)上是单调 函数增同学们再见
并画出它的图象解:f(-2)=(-2)2=4f(-1)=(-1)2=1f(2)=4f(1)=1f(-x)=(-x)2=x 2同学们发现了什么规律?f(-2)=f(2)
f(-1)=f(1)
f(-x)=f(x)x-xf(x)f(-x)观察知函数 f(x)=x2
对定义域内一切 x 有
f(-x)=f(x) 成立它的图象关于 y 轴对称偶函数定义: 如果对于f(x)定义域内的任意一个x, 都有
f(-x)=f(x), 那么函数f(x)就叫偶函数.前面讨论的函数 f(x)=x2 按定义是偶函数函数 f(x)=x4 是偶函数吗?函数 f(x)=x10 是偶函数吗?函数 f(x)=x2n n∈Z 是偶函数吗?函数 f(x)=x2n n∈Z 一定是偶函数 引入问题2 已知函数f(x)=x3求f(-2),f(2), f(-1),f(1),及f(-x)
并画出它的图象解:f(-2)=(-2)3=-8 f(2)=22=8 f(-1)=(-1)3=-1 f(1)=13=1 f(-x)=(-x)3=-x 3同学们发现了什么规律?f(-2)=-f(2)
f(-1)=-f(1)
f(-x)=-f(x)xf(x)-xf(-x)观察知函数 f(x)=x3
对定义域内一切 x 有
f(-x)=-f(x) 成立它的图象关于原点对称奇函数定义:如果对于f(x)定义域内的任意一个x, 都有
f(-x)=-f(x), 那么函数f(x)就叫奇函数.前面讨论的函数 f(x)=x3 按定义是奇函数函数 f(x)=x5 是奇函数吗?函数 f(x)=x13 是奇函数吗?函数 f(x)=x2n-1 n∈Z 是奇函数吗?函数 f(x)=x2n-1 n∈Z 一定是奇函数 如果一个函数f(x)是奇函数或偶函数,
那么我们就说函数 f(x) 具有奇偶性。探究:具有奇偶性的函数,其定义域具有怎样的特点?具有奇偶性的函数,其定义域关于数“0”对称对奇函数、偶函数定义的说明:(1)定义域关于原点对称是函数具有奇偶性
的前提条件Oab-a-b(2)奇、偶函数定义的逆命题也成立,即:
若f(x)为奇函数, 则f(-x)=-f(x)成立。
若f(x)为偶函数, 则f(-x)= f(x) 成立。(3) 如果一个函数f(x)是奇函数或偶函数
那么我们就说函数 f(x) 具有奇偶性。奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))奇函数的图象
关于原点对称偶函数的图象
关于 y 轴对称练习1. 说出下列函数的奇偶性:偶函数奇函数①f(x)=x4 ________ ④ f(x)= x -1 ________② f(x)=x ________⑤f(x)=x -2 __________③ f(x)=x5 __________⑥f(x)=x -3 ________ 说明:对于形如 f(x)=x n 的函数,
若n为偶数,则它为偶函数。
若n为奇数,则它为奇函数。奇函数奇函数奇函数偶函数例1 已知函数y=f(x)是偶函数,它在y轴右边 的图象如图,画出它在 y 轴左边的图象oyx解:画法略 y x 0例2 判断函数 f(x)=x3+2x 的奇偶性解:函数的定义域是 R ∵ f(-x)=(-x)3+2(-x)=-x 3 -2x=-f(x)∴ f(x) 是奇函数=-(x 3+2x)研究函数的奇偶性
必须首先讨论函数的定义域
仅当函数的定义域关于原点对称
才能说它具有奇偶性例3 判断函数 f(x)=2x4+3x2 的奇偶性解:函数的定义域是 R ∵ f(-x)=2(-x)4+3(-x)2=2x4 +3x2=f(x)∴ f(x) 是偶函数研究函数的奇偶性
必须首先讨论函数的定义域
仅当函数的定义域关于原点对称
才能说它具有奇偶性例4判断函数 f(x)=5 的奇偶性解:函数的定义域是 R ∵ f(-x)=5=f(x),且 f(-x)≠-f(x)∴ f(x) 是偶函数不是奇函数判断函数 f(x)=0 的奇偶性 ∵ f(-x)=0=f(x) 且 -f(x)=0=f(-x) ∴ f(x) 既是奇函数又是偶函数说明:定义域关于原点对称的函数
若是非零的常数函数是偶函数
在定义域内恒等于零的函数
既是奇函数又是偶函数例5 判断函数 f(x)=x+1 的奇偶性解:函数的定义域是 R ∵ f(-x)=(-x)+1=-x+1 ∴ f(-x)≠f(x) ∵ -f(x)=-(x+1)=-x-1 ∴ f(-x)≠-f(x) 因此,f(x) 是非奇非偶函数另解:由图象知,不具有对称性 由此可知 f(x) 是非奇非偶函数例6 判断函数 f(x)=x2 x∈[-1,3] 的奇偶性解:∵ 函数的定义域是 [-1,3]不是关于原点对称∴ f(x) 是非奇非偶函数另解:∵ 图象不具有对称性 ∴ f(x) 是非奇非偶函数说明:根据奇偶性, 函数可划分为四类:奇函数-它的图象关于原点对称偶函数-它的图象关于 y 轴对称既奇又偶函数-在定义域内恒为零非奇非偶函数-图象不具有对称性课堂练习判断下列函数的奇偶性(不写证明过程)1 f(x)=x4-3x2+52 f(x)=x5-3x3+5x3 f(x)=x5-3/x3+54 f(x)=x+1/x5 f(x)=(x4-1)/x2偶函数偶函数奇函数奇函数非奇非偶函数思考题:1﹑函数f(x)是定义在R上的偶函数,
如果f(x)在x∈[0,+∞)上是单调增函数,那么f(x)在x∈(-∞,0)上是单调 函数。减2﹑函数f(x)是定义在R上的奇函数,
如果f(x)在x∈[0,+∞)上是单调增函数,那么f(x)在x∈(-∞,0)上是单调 函数增同学们再见
