函数单调性[上学期]
图片预览




文档简介
课件14张PPT。南师大二附中 朱斌
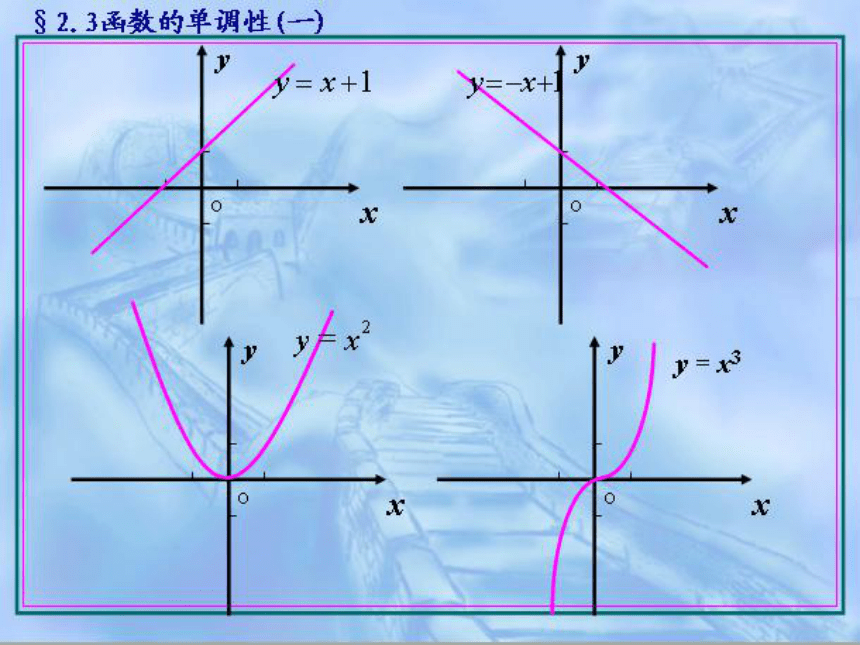
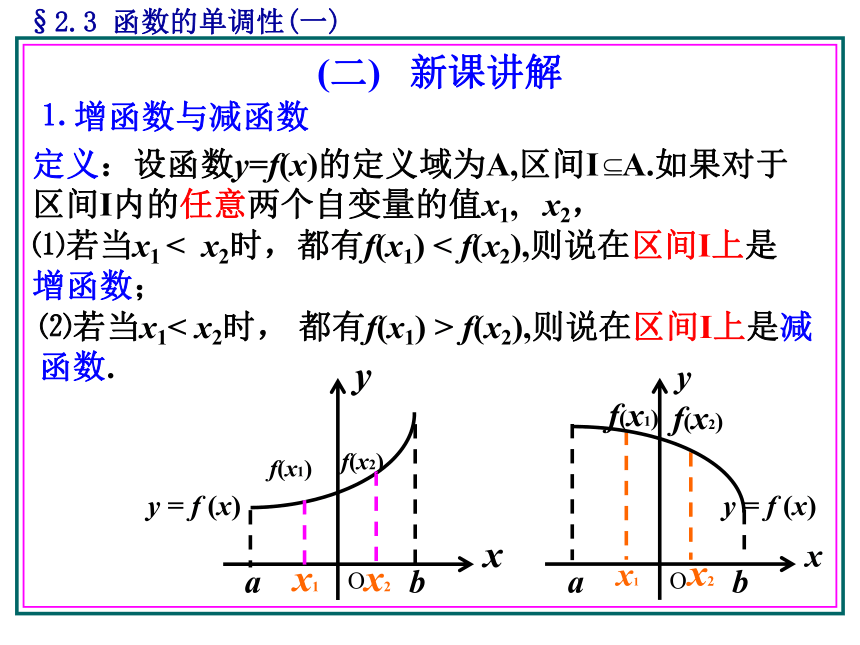
2006年9月22日数学教学课件函数的单调性 第一课时§2.3函数的单调性(一) 请同学们画出下列函数图象的简图 §2.3 函数的单调性(一)(二) 新课讲解⒈ 增函数与减函数定义:设函数y=f(x)的定义域为A,区间I A.如果对于区间I内的任意两个自变量的值x1, x2,⑴若当x1 < x2时,都有f(x1) < f(x2),则说在区间I上是增函数;⑵若当x1< x2时, 都有f(x1) > f(x2),则说在区间I上是减函数.y = f (x)y = f (x)§2.3 函数的单调性(一)⒉ 单调性与单调区间 在单调区间上,增函数的图象是 ,减函数的图象是 . 若函数y=f(x)在某个区间I是增函数或减函数,则就说函数y=f(x)在区间I上具有单调性,这一区间叫做函数y=f(x)的单调区间.此时也说函数y=f(x)是这一区间上的单调函数.上升的下降的 能否说,由于x=1时,y=3; x=2时,y=5;就说随着x的增大,函数值y也随着增大?
能否说,由于x=1,2,3,4,5,…时,相应地
y=3,5,7,9,…就说随着x的增大,函数值y也随着增大?思考:强调:取值的任意性.§2.3 函数的单调性(一)说明:(1)函数的单调性是在函数的定义域或其子区间上的
性质;
(2)函数的单调性是对某个区间而言的,在某一点上
不存在单调性,端点值有意义则闭,无意义则开;
(3)函数单调性的定义中,实际上含有两层意思:
①对于任意的 ,若 ,有 ,则称在 上是增函数;
②若 在 上是增函数,则当 时,就有 §2.3函数的单调性(一)3、定义的内涵与外延:
内涵:用自变量的变化来刻划函数值的变化规律.
外延:
①一般规律:自变量的变化与函数值的变化一致时是单调递增,自变量的变化与函数值的变化相反时是单调递减.
②几何特征:在自变量取值的区间上,若单调函数的图象上升则为增函数,图象下降则为减函数.§2.3函数的单调性(一)(三) 例题赏析例1、 如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,函数y=f(x)是增函数还是减函数. 解:函数f(x)的单调区间有[-5,-2],[-2,1],[1,3],[3,5],
其中f(x)在区间[-5,-2],[1,3]上是减函数,在区间[-2,1],[3,5]上是增函数.§2.3函数的单调性(一)例2 证明函数 在R上是增函数.根据定义证明函数单调性的一般步骤是:
⑴设 是给定区间内的任意两个值,且⑵作差 并将此差变形(要注意变形的程度)⑶判断 的正负(说理要充分)⑷根据 的符号确定其增减性§2.3函数的单调性(一)例3、画出下列函数图象,并写出单调区间:练习:
课本 P37§2.3 函数的单调性(一)(四)小结与归纳 ⒈讨论函数的单调性必须在定义域内进行,即函数的单调区间是其定义域的子集,因此讨论函数的单调性,必须先确定函数的定义域⒉根据定义证明函数单调性的一般步骤是:
⑴设 是给定区间内的任意两个值,且⑵作差 并将此差变形(要注意变形的程度)⑶判断 的正负(说理要充分)⑷根据 的符号确定其增减性再见谢谢指导
2006年9月22日数学教学课件函数的单调性 第一课时§2.3函数的单调性(一) 请同学们画出下列函数图象的简图 §2.3 函数的单调性(一)(二) 新课讲解⒈ 增函数与减函数定义:设函数y=f(x)的定义域为A,区间I A.如果对于区间I内的任意两个自变量的值x1, x2,⑴若当x1 < x2时,都有f(x1) < f(x2),则说在区间I上是增函数;⑵若当x1< x2时, 都有f(x1) > f(x2),则说在区间I上是减函数.y = f (x)y = f (x)§2.3 函数的单调性(一)⒉ 单调性与单调区间 在单调区间上,增函数的图象是 ,减函数的图象是 . 若函数y=f(x)在某个区间I是增函数或减函数,则就说函数y=f(x)在区间I上具有单调性,这一区间叫做函数y=f(x)的单调区间.此时也说函数y=f(x)是这一区间上的单调函数.上升的下降的 能否说,由于x=1时,y=3; x=2时,y=5;就说随着x的增大,函数值y也随着增大?
能否说,由于x=1,2,3,4,5,…时,相应地
y=3,5,7,9,…就说随着x的增大,函数值y也随着增大?思考:强调:取值的任意性.§2.3 函数的单调性(一)说明:(1)函数的单调性是在函数的定义域或其子区间上的
性质;
(2)函数的单调性是对某个区间而言的,在某一点上
不存在单调性,端点值有意义则闭,无意义则开;
(3)函数单调性的定义中,实际上含有两层意思:
①对于任意的 ,若 ,有 ,则称在 上是增函数;
②若 在 上是增函数,则当 时,就有 §2.3函数的单调性(一)3、定义的内涵与外延:
内涵:用自变量的变化来刻划函数值的变化规律.
外延:
①一般规律:自变量的变化与函数值的变化一致时是单调递增,自变量的变化与函数值的变化相反时是单调递减.
②几何特征:在自变量取值的区间上,若单调函数的图象上升则为增函数,图象下降则为减函数.§2.3函数的单调性(一)(三) 例题赏析例1、 如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,函数y=f(x)是增函数还是减函数. 解:函数f(x)的单调区间有[-5,-2],[-2,1],[1,3],[3,5],
其中f(x)在区间[-5,-2],[1,3]上是减函数,在区间[-2,1],[3,5]上是增函数.§2.3函数的单调性(一)例2 证明函数 在R上是增函数.根据定义证明函数单调性的一般步骤是:
⑴设 是给定区间内的任意两个值,且⑵作差 并将此差变形(要注意变形的程度)⑶判断 的正负(说理要充分)⑷根据 的符号确定其增减性§2.3函数的单调性(一)例3、画出下列函数图象,并写出单调区间:练习:
课本 P37§2.3 函数的单调性(一)(四)小结与归纳 ⒈讨论函数的单调性必须在定义域内进行,即函数的单调区间是其定义域的子集,因此讨论函数的单调性,必须先确定函数的定义域⒉根据定义证明函数单调性的一般步骤是:
⑴设 是给定区间内的任意两个值,且⑵作差 并将此差变形(要注意变形的程度)⑶判断 的正负(说理要充分)⑷根据 的符号确定其增减性再见谢谢指导
