函数单调性(苏教版)课件[上学期]

课件26张PPT。函数的单调性江苏省清江中学
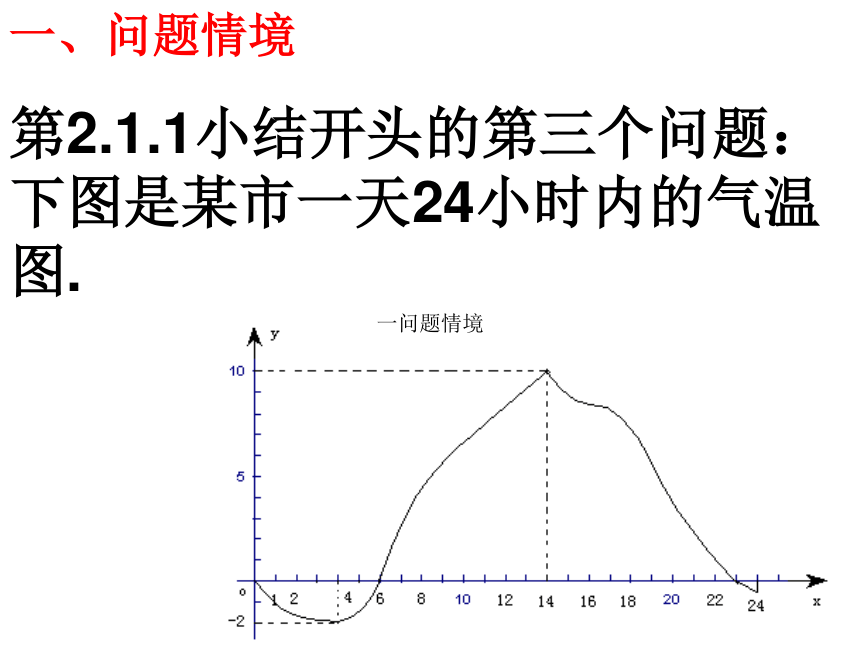
尚月如第2.1.1小结开头的第三个问题：
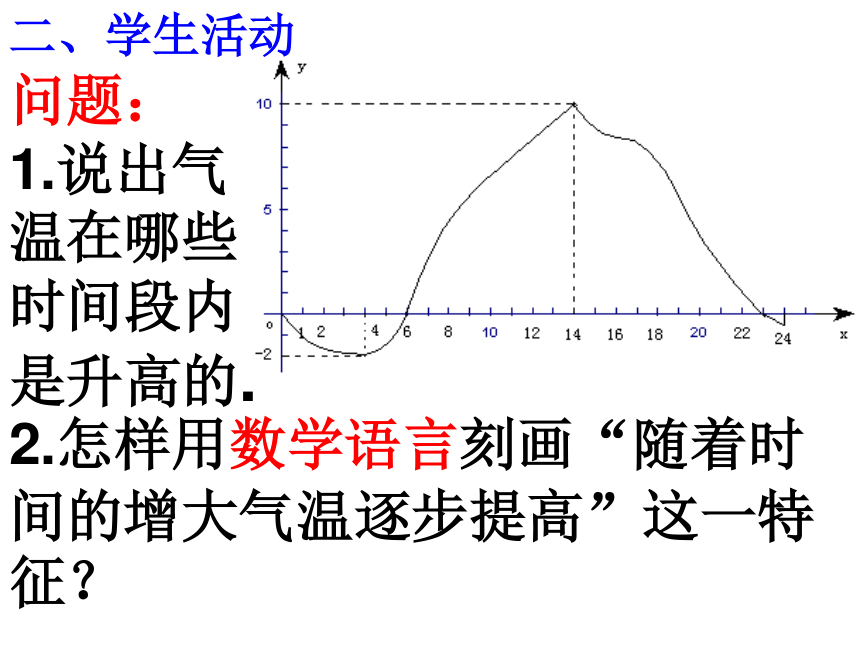
下图是某市一天24小时内的气温图.问题情境、问题情境问题：
1.说出气
温在哪些
时间段内
是升高的.2.怎样用数学语言刻画“随着时间的增大气温逐步提高”这一特征？二、学生活动问题1：观察下列函数的图象，指出图象变化的趋势.
在区间（－∞，+ ∞ ）内，
函数y＝2x+1图象在该区间
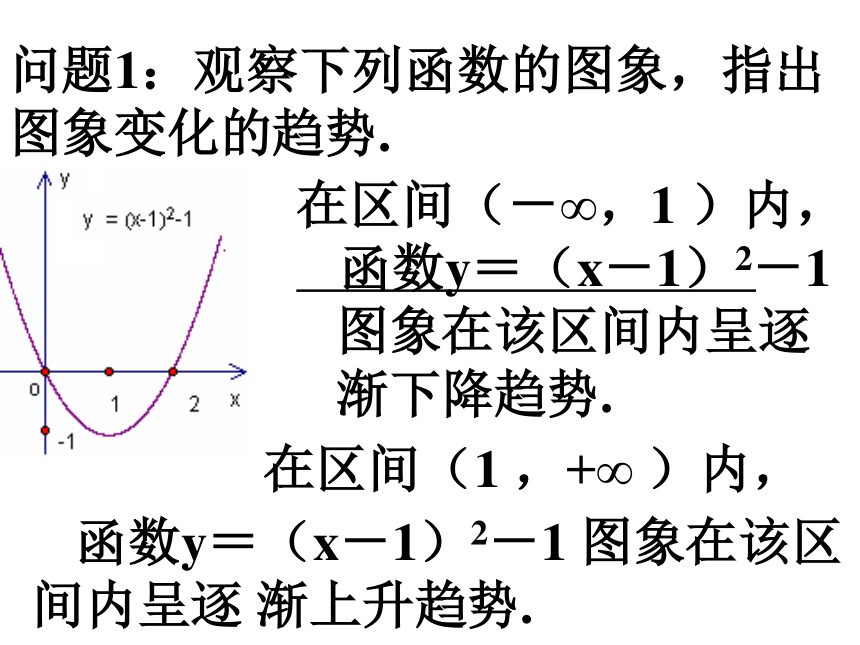
内呈逐渐上升趋势问题1：观察下列函数的图象，指出图象变化的趋势.
在区间（－∞，1 ）内，
在区间（1 ，+∞ ）内，
函数y＝（x－1）2－1
图象在该区间内呈逐
渐下降趋势. 函数y＝（x－1）2－1 图象在该区间内呈逐 渐上升趋势.问题1：观察下列函数的图象，指出图象变化的趋势.
在区间（0 ，+∞ ）内，
函数y＝ 图象在
该区间内呈逐 渐下降
趋势. 函数y＝ 图象在
该区间内呈逐 渐下降
趋势.函数的这种性质称为函数的单调性.问题3：如何用数学语言来准确地描述
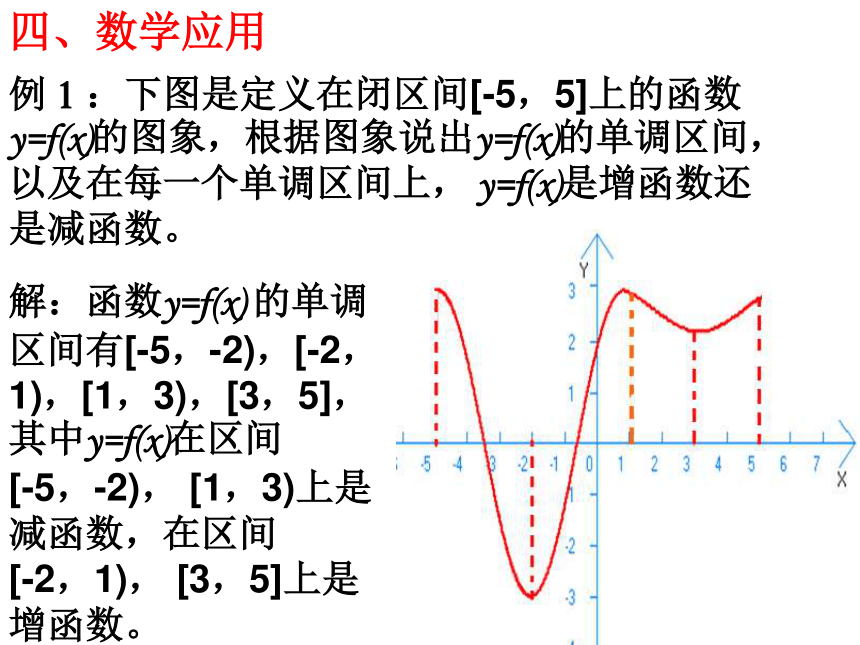
函数的单调性呢？三、建构数学例如，在区间（1， + ∞ ）上当x的值增大时，函数y的值也增大的事实应当如何表述？ 能不能由于x=1时，y=3；x=2时，y=5，就说随着x的增大，函数值y也随着增大？函数的单调性如果对于属于定义域I内某个区间上的任意两个自变量的值x1 ， x2 ，当x1 f(x2) ，那么就说f(x)在这个区间上是减函数。2. 定义如果函数y= f(x)在某个区间上是增函数或减函数，那么就说函数y= f(x)在这个区间上具有(严格的)单调性，这个区间叫做y= f(x)的单调区间。一般地，对于函数 y = f(x)的定义域为I定义域I内某个区间定义域I内某个区间任意两个自变量任意两个自变量例１：下图是定义在闭区间[-5，5]上的函数y=f(x)的图象，根据图象说出y=f(x)的单调区间，以及在每一个单调区间上， y=f(x)是增函数还是减函数。解：函数y=f(x) 的单调区间有[-5，-2)，[-2，1)，[1，3)，[3，5]，其中y=f(x)在区间
[-5，-2)， [1，3)上是减函数，在区间
[-2，1)， [3，5]上是增函数。四、数学应用例2 作出下列函数的图象，并写出函数的单调区间：
（1）y=－x2＋2 ； （2）y=提问：能不能说，函数y=上是单调减函数？（1）函数y=－x2＋2在（－∞，0）上是单调增函数，
在（ 0 ，+∞）上是单调增函数减函数.（2）函数y=在（ 0 ，+∞）上也是单调减函数.在（－∞，0）上是单调减函数，在（－∞，0）Ｕ（ 0 ，+∞）例3.观察下列函数的图象，并指出它们是否为定义
域上的增函数： 能不能不通过观察函数的图象就能知道
函数的单调性呢？ 在不太好画出函数的图象时如何判断
函数的单调性呢？ 函数y＝1/x2(x＞0)的是单调增函数，还是单调减函数呢？证明：（条件）（论证结果）（结论）1. 在这个区间上任取两个自变 量x1、x2, 且x1< x2 .
2.作差（作商）并将差f(x1)－ f(x2) 化简变形成最简形式.
3.判断符号.
4.得出结论.用函数单调性定义判定或证明函数单调性的一般步骤：例5 试判断函数证明：巩固练习：
课本P37 练习 1、5、6、8.例6 已知函数f(x)在（0，+ ）上是减函数，
求f(a2-a+1) 与f( )的大小
解：因为f(x)在（0，+ ）是减函数
因为a2-a+1=（a- )2+ ≥ >0
所以f(a2-a+1) ≤ f( )例7 已知函数f(x)在（-1，3）上是减函数，且 f(2a-1) - f(a+1) >0，求实数 a 的范围。解得：所以实数a的取值范围是：解：由函数f(x)在（-1，1）上是减函数得：①2a-1课本P37 练习 3方法二：分析函数值y随自变量x大小的变化情况。方法一：观察函数的图象。方法三：利用函数单调性的定义。判断函数单调区间的常用方法：五、回顾小结本节课主要学习了函数单调性的概念、判断
函数在某个区间上的单调性的方法以及函数
单调性的一些简单运用.1. 在这个区间上任取两个自变 量x1、x2, 且x1< x2 .
2.作差，并将差f(x1)－ f(x2) 化简变形成最简形式（有时也通过作商比较f(x1)与 f(x2) 的大小）.
3.判断f(x1)－ f(x2)符号.
4.得出结论.用函数单调性定义判定或证明函数单调性的一般步骤：课后作业
课本P37
2、4、5.