函数的单调性[上学期]
图片预览

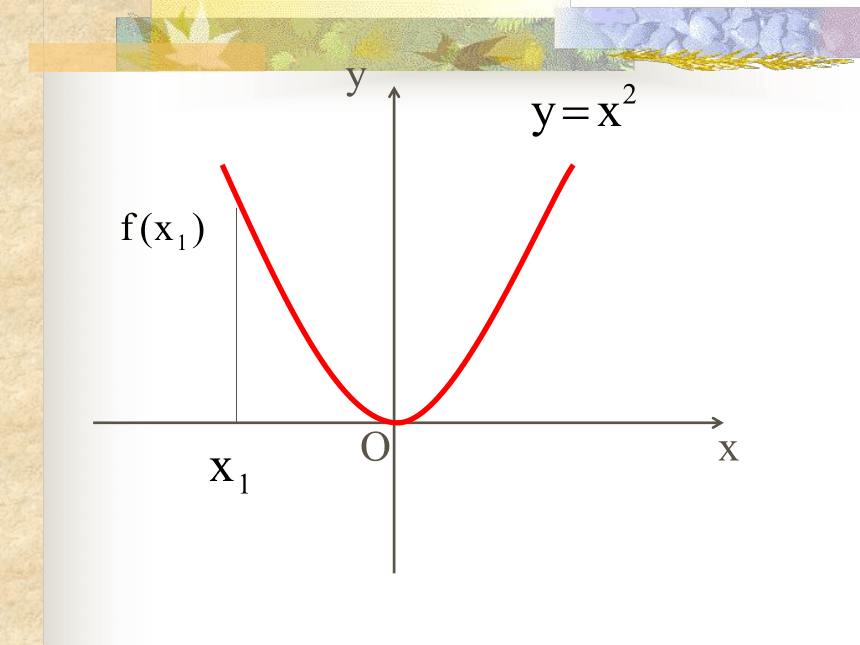
文档简介
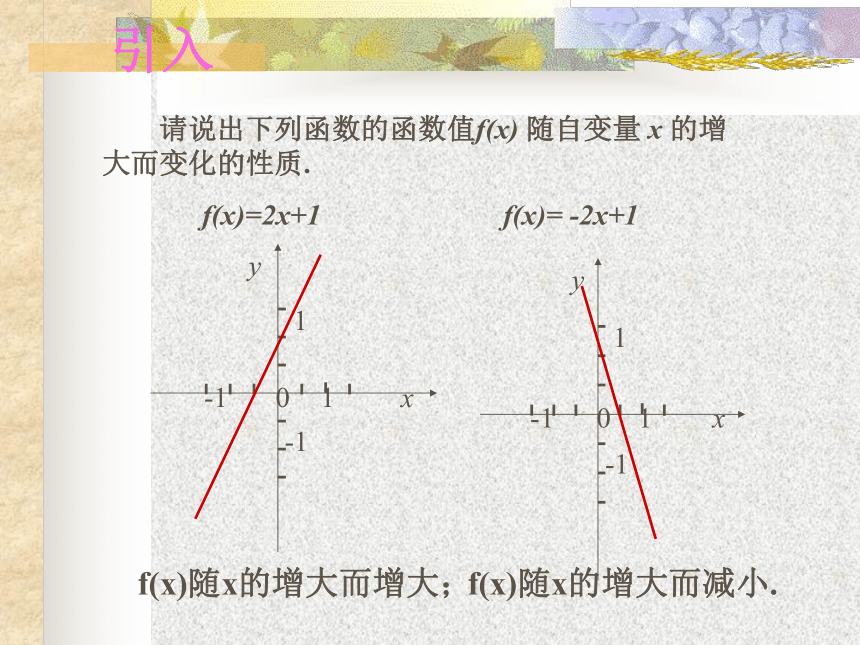
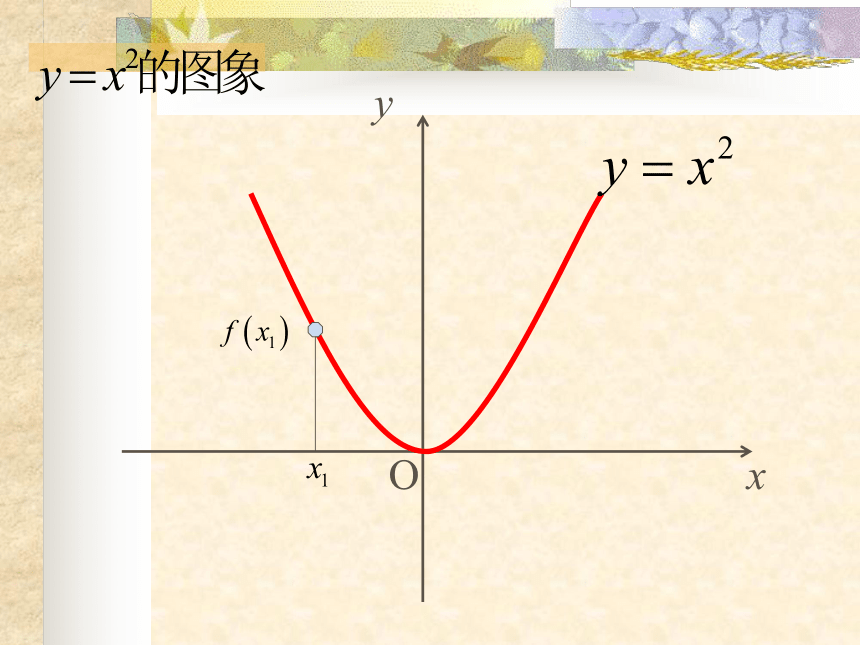
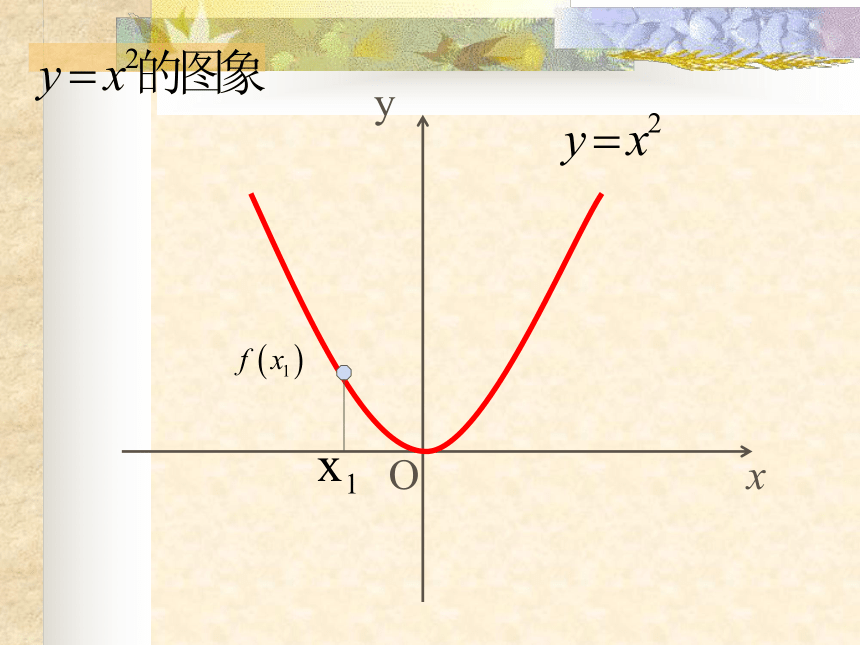
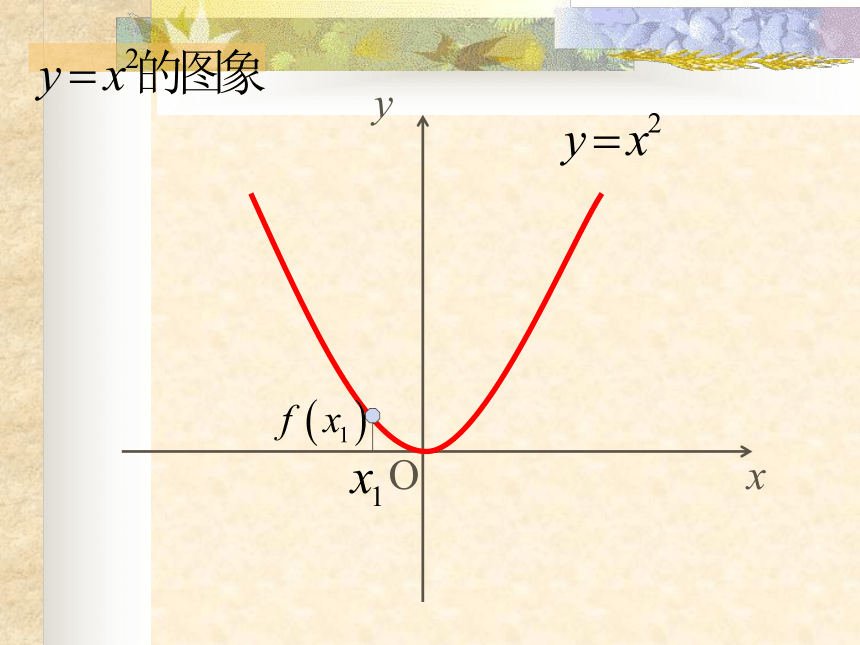
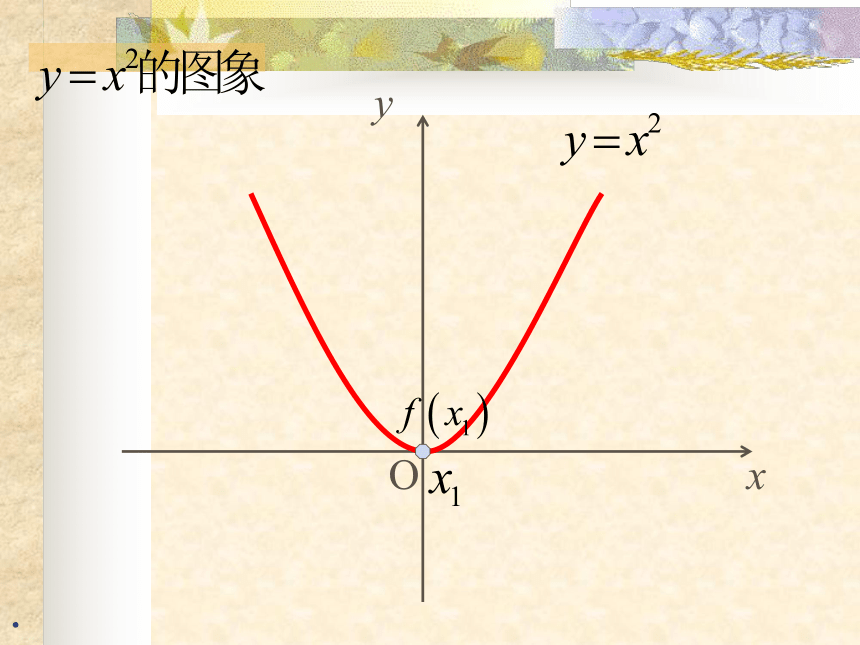
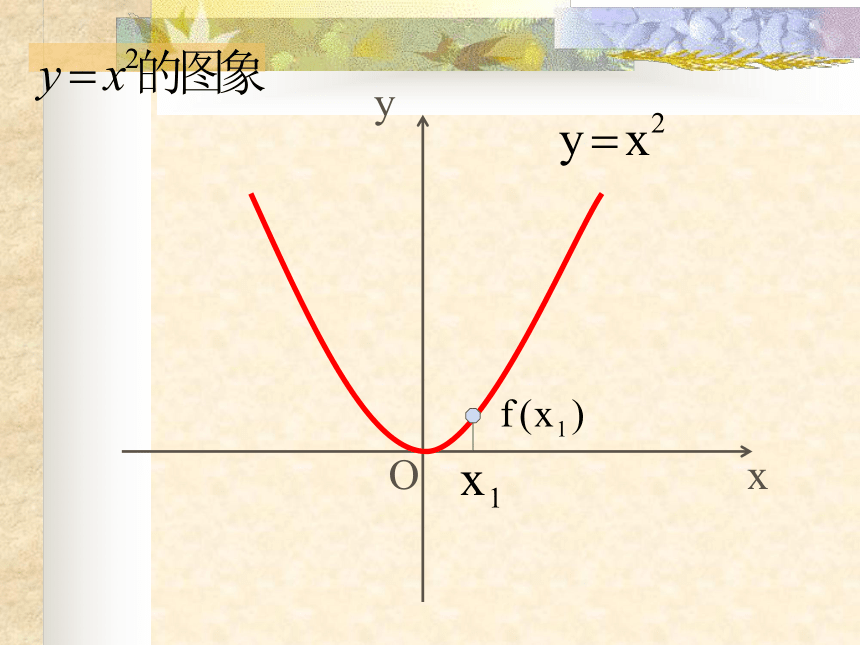
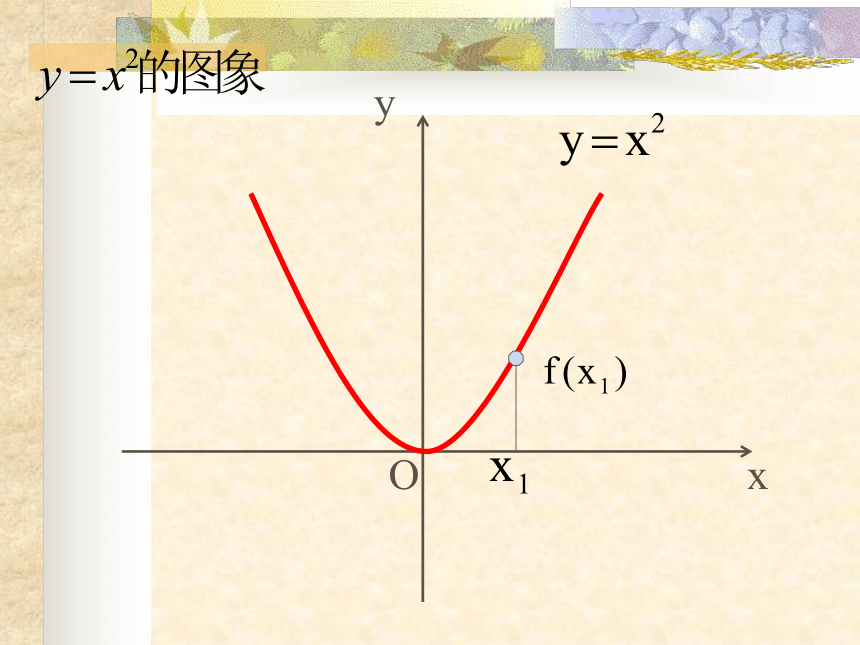
课件23张PPT。函数的单调性 请说出下列函数的函数值f(x) 随自变量 x 的增大而变化的性质.f(x)=2x+1f(x)= -2x+1引入f(x)随x的增大而增大;f(x)随x的增大而减小.OxyOxyOxyOxyOxy.OxyOxyOxyOxyOxy观察xy0y=x2图象在y轴右侧部分从左到右是上升的,即当x∈ [0,+∞ )时,y随x增大而增大;任意 x1 , x2 ∈ [0,+∞ ),且x1< x2,都有f(x1) < f(x2),那么就说 y=x2 在[0,+∞ )上是增函数.任意 x1 , x2 ∈ (-∞,0 ),且x1< x2,都有f(x1) > f(x2),那么就说 y=x2 在(-∞,0 )上是减函数.x1x2f(x1)f(x2)函数 y=x3 在R上是增函数图象在y轴左侧部分是从左到右下降的,即当x∈ (-∞,0 )时,y随x增大而减小.y=x3 函数f(x)在给定区间D上为增函数.一般地,设函数f(x)的定义域为I,对于I内的某个区间D, 函数f(x)在给定区间D上为减函数.定义xy给定区间、任意性 以y=x2为例:
试问:我们能不能说 y=x2增函数还是减函数?-2-112(2)函数单调性反映的是函数在相应区间上函数值y随x而变化的趋势.
在单调区间上从左往右看增函数的图象是上升的,减函数的图象是下降的.(1)函数是增函数还是减函数,是对定义域内某个区间而言的,并且单调区间是函数定义域的子集.内涵(3)函数的单调性也叫增减性.外延例1如图定义在闭区间 [-5,5] 上的函数y= f(x) 的图象,根据图象说出 y= f(x)的单调区间,以及在每一单调区间上 , y= f(x)是增函数还是减函数?解:函数y= f(x)的单调区间有[-5,2),[-2,1),[1,3),[3,5]。其中 y= f(x)在区间[-5,2), [1,3)上是减函数,在[-2,1), [3,5]是增函数。练习注意:函数y= f(x)在[-5,2)∪[1,3)上不是减函数。可以说:函数y= f(x)在[-5,2)和[1,3)上是减函数若函数在两个区间上都是减函数,则在它们的并集上不一定是减函数.例2单调递减区间:单调递增区间:练习1.课本P59练习第1题.2.依据图象判断下列函数的单调性.2小结1、函数的单调性——增函数和减函数、 函数的单调区间.
函数y= f(x)在其单调递增区间上的图象是上升的,在单调递减区间上的图象是下降的.
2、根据函数的图象确定函数的单调性、单调区间.并注意写单调区间不要轻易用并集连接。
3、用定义判断函数的单调性
其步骤:作差—变形—定号—判断.作业1.课本 P60 习题2.3 1~5
2. 导学大课堂
试问:我们能不能说 y=x2增函数还是减函数?-2-112(2)函数单调性反映的是函数在相应区间上函数值y随x而变化的趋势.
在单调区间上从左往右看增函数的图象是上升的,减函数的图象是下降的.(1)函数是增函数还是减函数,是对定义域内某个区间而言的,并且单调区间是函数定义域的子集.内涵(3)函数的单调性也叫增减性.外延例1如图定义在闭区间 [-5,5] 上的函数y= f(x) 的图象,根据图象说出 y= f(x)的单调区间,以及在每一单调区间上 , y= f(x)是增函数还是减函数?解:函数y= f(x)的单调区间有[-5,2),[-2,1),[1,3),[3,5]。其中 y= f(x)在区间[-5,2), [1,3)上是减函数,在[-2,1), [3,5]是增函数。练习注意:函数y= f(x)在[-5,2)∪[1,3)上不是减函数。可以说:函数y= f(x)在[-5,2)和[1,3)上是减函数若函数在两个区间上都是减函数,则在它们的并集上不一定是减函数.例2单调递减区间:单调递增区间:练习1.课本P59练习第1题.2.依据图象判断下列函数的单调性.2小结1、函数的单调性——增函数和减函数、 函数的单调区间.
函数y= f(x)在其单调递增区间上的图象是上升的,在单调递减区间上的图象是下降的.
2、根据函数的图象确定函数的单调性、单调区间.并注意写单调区间不要轻易用并集连接。
3、用定义判断函数的单调性
其步骤:作差—变形—定号—判断.作业1.课本 P60 习题2.3 1~5
2. 导学大课堂
