函数的周期性[下学期]
图片预览




文档简介
课件12张PPT。延庆三中青年教师考核课函数的周期性教师:卢冬宝
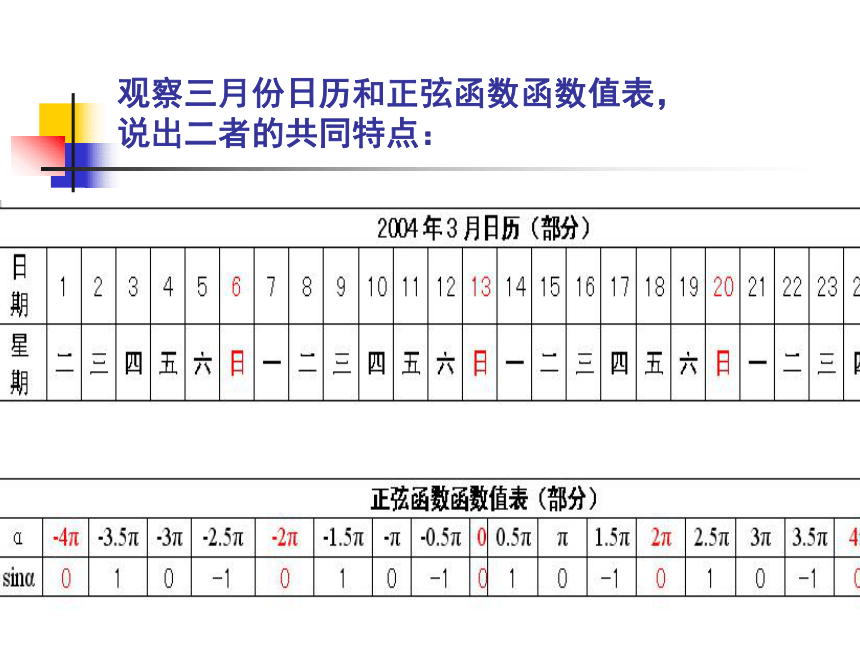
时间: 2005.3The Periodicity of Function 观察三月份日历和正弦函数函数值表, 说出二者的共同特点:函数周期性的定义 对于函数y=f(x),如果存在一个 T,使得当 时,
都成立,那么就把函数
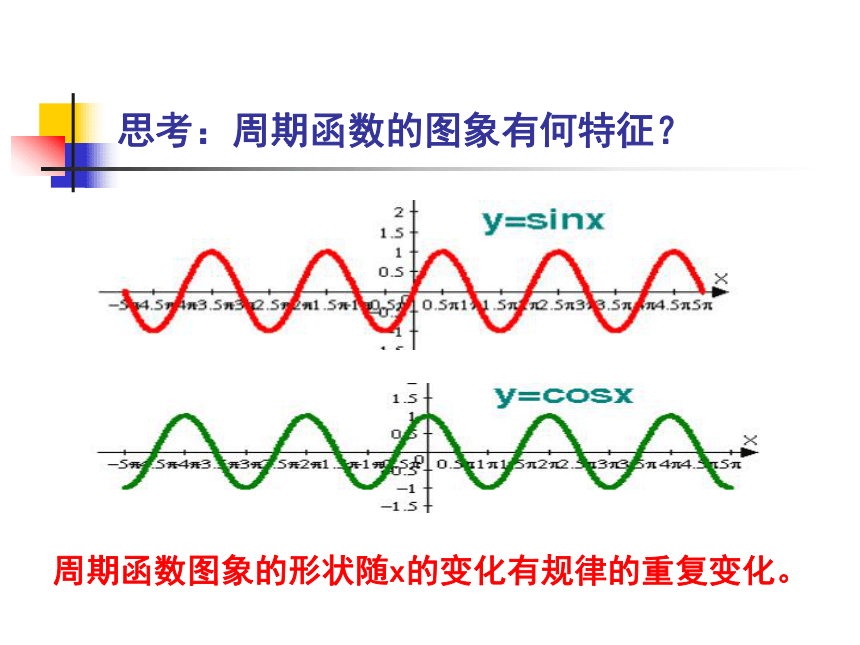
y=f(x)叫做周期函数,不为零的常数T叫做这个函数的周期。 f( )=f( )不为零的常数sin(x+ )=sinx2kπ 正弦函数和余弦函数均为周期函数, 且周期 T=2kπ (k∈Z且k≠0) x取定义域内的每一个值cos(x+ )=cosx2kπ(k∈Z且k≠0)x+T x思考:周期函数的图象有何特征?周期函数图象的形状随x的变化有规律的重复变化。 思考: 函数f(x)=x2是否为周期函数?如果是,周期是多少?令f(x+T)=f(x), 即(x+T)2=x2 即x2+2xT+T2=x2, 所以2xT+T2=0 即T(2x+T)=0所以T=0或T=-2x 因为T=0或T=-2x 均不符合函数周期的要求,所以函数f(x)=x2不是周期函数。最小正周期的概念: 对于一个周期函数f(x),如果它所有的周期中存在一个
最小的正数,那么这个最小正数叫f(x)的最小正周期。sin(x+ )=sinx
cos(x+ )=cosx2π
2π 自变量x只要并且至少增加到x+2π时,
函数值才能重复取得。正弦函数和余弦函数的最小正周期是2π。 最小正周期在图象上的意义 :最小正周期是函数图象重复出现需要的最短距离。例题:求下列函数的周期:(1)y=3cosx 解:因为3cos(x+ )=3cosx(x只要且至少增加到x+2π)2π所以原函数的周期是2π。 (2)y=sin(x+π/4)解:因为
sin[(x+ )+π/4]= sin(x+π/4)2π所以原函数的周期是2π。(3)y=sin2x解:因为sin[2(x+ )]
=sin2x=Sin[2x+2π]π所以原函数的周期是π。 4π所以原函数的周期是4π。所以原函数的周期是 。结论:形如y=Asin(ωx+φ) 或y=Acos(ωx+φ) (A,ω,φ为常数,A?0, x?R) 的函数的周期为T= 课上练习:求下列函数的周期(直接用结论做):(1)解:
∵ω=1
∴原函数的周期为
T=2π/ω=2π三角函数具有周期性的本质原因:三角函数值的大小是由角的终边在坐标系中的位置决定的,而在角的终边转动时,终边每转过2π,都会与原来的终边重合,这样三角函数值就会周而复始地出现。课堂小结:2. 正弦函数y=sinx和余弦函数y=cosx均为周期函数, 且(最小正)周期为2π。1. 函数周期性的概念。4. 函数周期性的用途。课后作业:教材:P57-5
思考题:常数函数f(x)=1是否为周期函数?如果是,此函数的(一般)周期为多少?此函数是否存在最小正周期?最小正周期是多少? 如果需要转载,请勿删除以下信息,多谢:
作者:卢冬宝
单位:北京市延庆县第三中学
邮箱:ludongbao@163.com
个人网页:http://ludongbao.51.net
欢迎光临数学双语教学网:http://www.bilingual-teach.com
时间: 2005.3The Periodicity of Function 观察三月份日历和正弦函数函数值表, 说出二者的共同特点:函数周期性的定义 对于函数y=f(x),如果存在一个 T,使得当 时,
都成立,那么就把函数
y=f(x)叫做周期函数,不为零的常数T叫做这个函数的周期。 f( )=f( )不为零的常数sin(x+ )=sinx2kπ 正弦函数和余弦函数均为周期函数, 且周期 T=2kπ (k∈Z且k≠0) x取定义域内的每一个值cos(x+ )=cosx2kπ(k∈Z且k≠0)x+T x思考:周期函数的图象有何特征?周期函数图象的形状随x的变化有规律的重复变化。 思考: 函数f(x)=x2是否为周期函数?如果是,周期是多少?令f(x+T)=f(x), 即(x+T)2=x2 即x2+2xT+T2=x2, 所以2xT+T2=0 即T(2x+T)=0所以T=0或T=-2x 因为T=0或T=-2x 均不符合函数周期的要求,所以函数f(x)=x2不是周期函数。最小正周期的概念: 对于一个周期函数f(x),如果它所有的周期中存在一个
最小的正数,那么这个最小正数叫f(x)的最小正周期。sin(x+ )=sinx
cos(x+ )=cosx2π
2π 自变量x只要并且至少增加到x+2π时,
函数值才能重复取得。正弦函数和余弦函数的最小正周期是2π。 最小正周期在图象上的意义 :最小正周期是函数图象重复出现需要的最短距离。例题:求下列函数的周期:(1)y=3cosx 解:因为3cos(x+ )=3cosx(x只要且至少增加到x+2π)2π所以原函数的周期是2π。 (2)y=sin(x+π/4)解:因为
sin[(x+ )+π/4]= sin(x+π/4)2π所以原函数的周期是2π。(3)y=sin2x解:因为sin[2(x+ )]
=sin2x=Sin[2x+2π]π所以原函数的周期是π。 4π所以原函数的周期是4π。所以原函数的周期是 。结论:形如y=Asin(ωx+φ) 或y=Acos(ωx+φ) (A,ω,φ为常数,A?0, x?R) 的函数的周期为T= 课上练习:求下列函数的周期(直接用结论做):(1)解:
∵ω=1
∴原函数的周期为
T=2π/ω=2π三角函数具有周期性的本质原因:三角函数值的大小是由角的终边在坐标系中的位置决定的,而在角的终边转动时,终边每转过2π,都会与原来的终边重合,这样三角函数值就会周而复始地出现。课堂小结:2. 正弦函数y=sinx和余弦函数y=cosx均为周期函数, 且(最小正)周期为2π。1. 函数周期性的概念。4. 函数周期性的用途。课后作业:教材:P57-5
思考题:常数函数f(x)=1是否为周期函数?如果是,此函数的(一般)周期为多少?此函数是否存在最小正周期?最小正周期是多少? 如果需要转载,请勿删除以下信息,多谢:
作者:卢冬宝
单位:北京市延庆县第三中学
邮箱:ludongbao@163.com
个人网页:http://ludongbao.51.net
欢迎光临数学双语教学网:http://www.bilingual-teach.com
