29.5正多边形与圆 达标测评(无答案) 2022-2023学年冀教版九年级数学下册
文档属性
| 名称 | 29.5正多边形与圆 达标测评(无答案) 2022-2023学年冀教版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 317.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览

文档简介
29.5正多边形与圆达标测评
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,四边形内接于,若,则( )
A. B. C. D.
2、如图所示的正八边形的边长为2,则对角线的长为( )
A. B.4 C. D.6
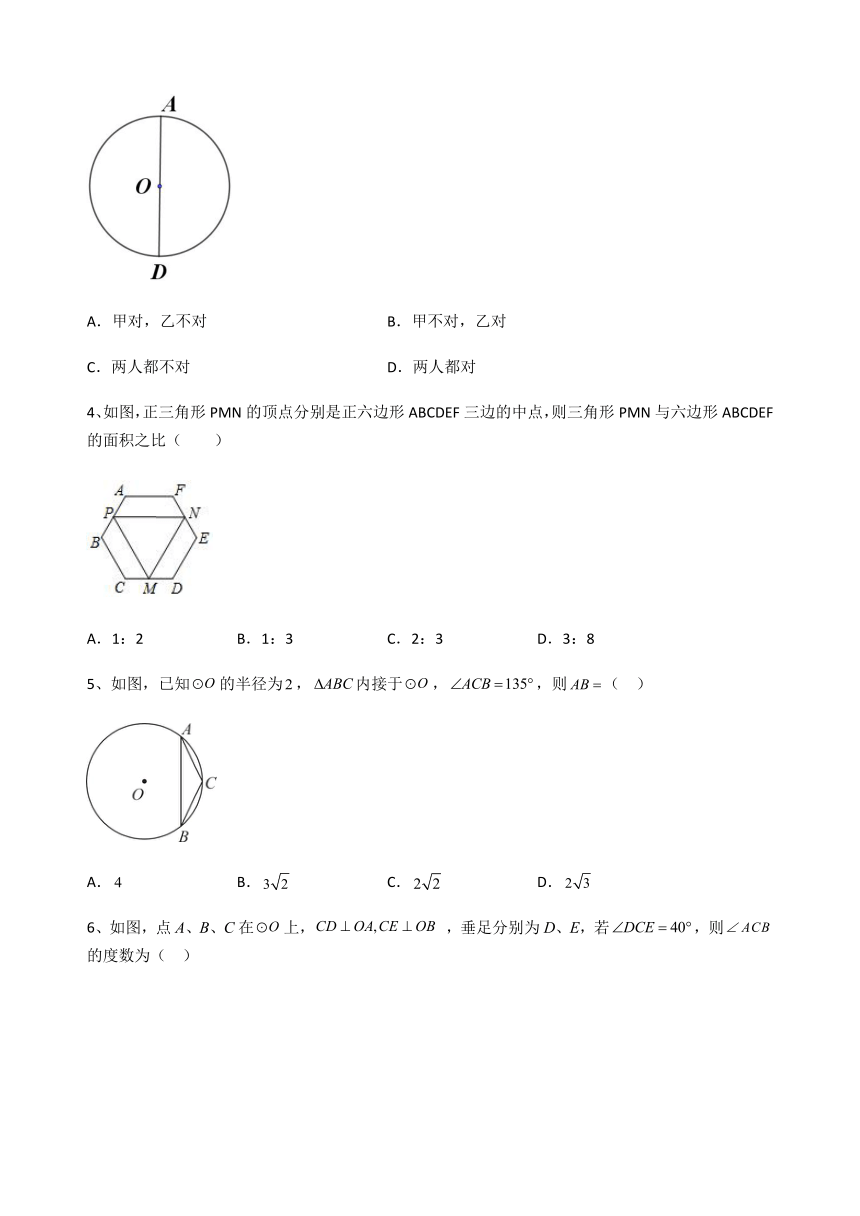
3、如图,为直径,作的内接正六边形,甲、乙两人的作法分别如下:
甲:1.作的中垂线,交圆于两点;2.作的中垂线,交圆于两点;3.顺次连接六个点,六边形即为所求;
乙:1.以为圆心,长为半径作弧,交圆于两点;2.以为圆心,长为半径作弧,交圆于两点;3.顺次连接六个点,六边形即为所求;
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都不对 D.两人都对
4、如图,正三角形PMN的顶点分别是正六边形ABCDEF三边的中点,则三角形PMN与六边形ABCDEF的面积之比( )
A.1:2 B.1:3 C.2:3 D.3:8
5、如图,已知的半径为,内接于,,则( )
A. B. C. D.
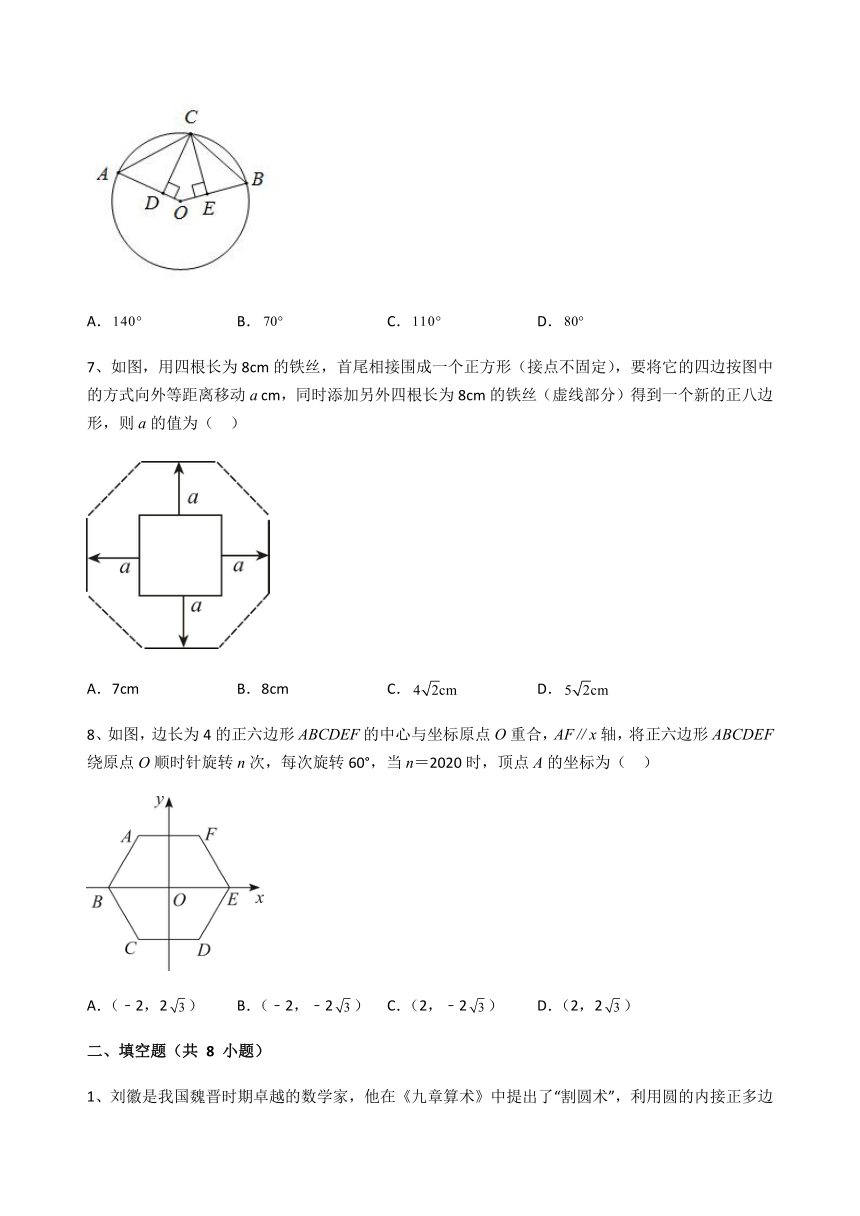
6、如图,点A、B、C在上, ,垂足分别为D、E,若,则的度数为( )
A. B. C. D.
7、如图,用四根长为8cm的铁丝,首尾相接围成一个正方形(接点不固定),要将它的四边按图中的方式向外等距离移动a cm,同时添加另外四根长为8cm的铁丝(虚线部分)得到一个新的正八边形,则a的值为( )
A.7cm B.8cm C. D.
8、如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
二、填空题(共 8 小题)
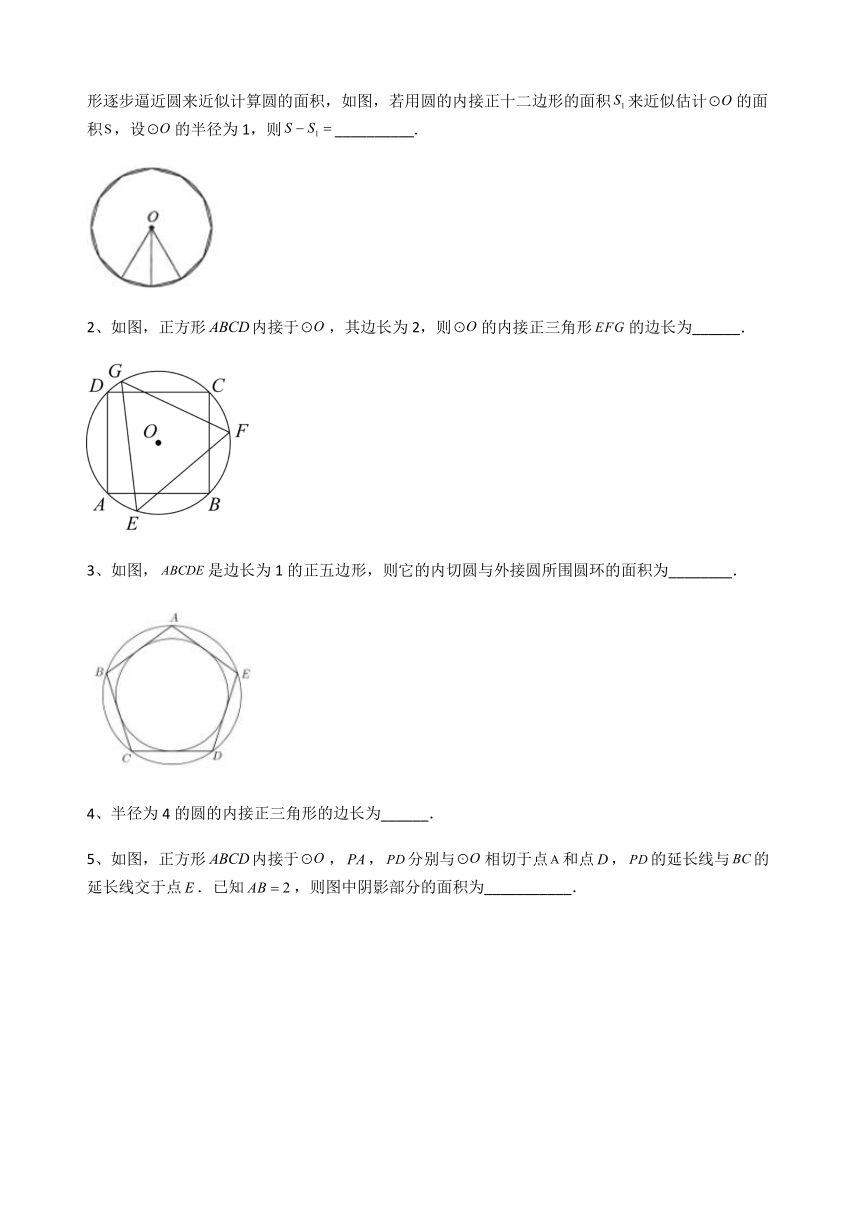
1、刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图,若用圆的内接正十二边形的面积来近似估计的面积,设的半径为1,则__________.
2、如图,正方形内接于,其边长为2,则的内接正三角形的边长为______.
3、如图,是边长为1的正五边形,则它的内切圆与外接圆所围圆环的面积为________.
4、半径为4的圆的内接正三角形的边长为______.
5、如图,正方形内接于,,分别与相切于点和点,的延长线与的延长线交于点.已知,则图中阴影部分的面积为___________.
6、如图,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形面积平分,则直线l被正六边形所截的线段长是_____.
7、如图,四边形是的内接正方形,E是的中点,交于点F,则___________度.
8、如图,AB、CD为一个正多边形的两条边,O为该正多边形的中心,若∠ADB=12°,则该正多边形的边数为 _____.
三、解答题(共 5 小题)
1、如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;(2)连接OF,OG,求∠OGF.
2、如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.
3、如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,∠ADB=45°. 求⊙O半径的长.
4、(1)如图,AB是半圆的直径,点C在半圆外,请仅用无刻度的直尺画出△ABC的三条高的交点;
(2)已知⊙O如图所示.
①求作⊙O的内接正方形(尺规作图,保留作图痕迹,不写作法);
②若⊙O的半径为4,则它的内接正方形的边长为_______________.
5、如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,四边形内接于,若,则( )
A. B. C. D.
2、如图所示的正八边形的边长为2,则对角线的长为( )
A. B.4 C. D.6
3、如图,为直径,作的内接正六边形,甲、乙两人的作法分别如下:
甲:1.作的中垂线,交圆于两点;2.作的中垂线,交圆于两点;3.顺次连接六个点,六边形即为所求;
乙:1.以为圆心,长为半径作弧,交圆于两点;2.以为圆心,长为半径作弧,交圆于两点;3.顺次连接六个点,六边形即为所求;
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都不对 D.两人都对
4、如图,正三角形PMN的顶点分别是正六边形ABCDEF三边的中点,则三角形PMN与六边形ABCDEF的面积之比( )
A.1:2 B.1:3 C.2:3 D.3:8
5、如图,已知的半径为,内接于,,则( )
A. B. C. D.
6、如图,点A、B、C在上, ,垂足分别为D、E,若,则的度数为( )
A. B. C. D.
7、如图,用四根长为8cm的铁丝,首尾相接围成一个正方形(接点不固定),要将它的四边按图中的方式向外等距离移动a cm,同时添加另外四根长为8cm的铁丝(虚线部分)得到一个新的正八边形,则a的值为( )
A.7cm B.8cm C. D.
8、如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
二、填空题(共 8 小题)
1、刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图,若用圆的内接正十二边形的面积来近似估计的面积,设的半径为1,则__________.
2、如图,正方形内接于,其边长为2,则的内接正三角形的边长为______.
3、如图,是边长为1的正五边形,则它的内切圆与外接圆所围圆环的面积为________.
4、半径为4的圆的内接正三角形的边长为______.
5、如图,正方形内接于,,分别与相切于点和点,的延长线与的延长线交于点.已知,则图中阴影部分的面积为___________.
6、如图,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形面积平分,则直线l被正六边形所截的线段长是_____.
7、如图,四边形是的内接正方形,E是的中点,交于点F,则___________度.
8、如图,AB、CD为一个正多边形的两条边,O为该正多边形的中心,若∠ADB=12°,则该正多边形的边数为 _____.
三、解答题(共 5 小题)
1、如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;(2)连接OF,OG,求∠OGF.
2、如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.
3、如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,∠ADB=45°. 求⊙O半径的长.
4、(1)如图,AB是半圆的直径,点C在半圆外,请仅用无刻度的直尺画出△ABC的三条高的交点;
(2)已知⊙O如图所示.
①求作⊙O的内接正方形(尺规作图,保留作图痕迹,不写作法);
②若⊙O的半径为4,则它的内接正方形的边长为_______________.
5、如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
