2022-2023学年沪科版数学八年级下册第18章 勾股定理 同步练习 (含简单答案)
文档属性
| 名称 | 2022-2023学年沪科版数学八年级下册第18章 勾股定理 同步练习 (含简单答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 433.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览


文档简介
第18章 勾股定理 同步练习 沪科版数学八年级下册
一、单选题
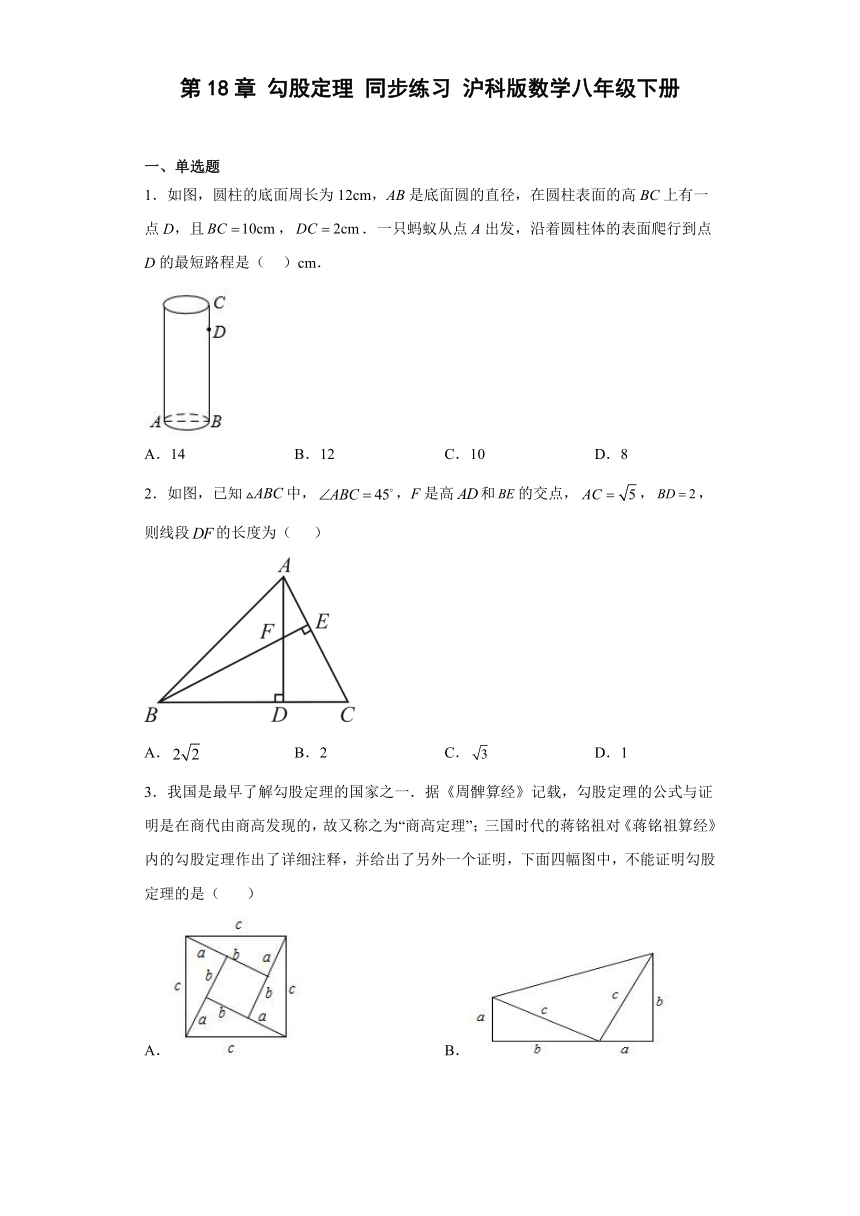
1.如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC上有一点D,且,.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.
A.14 B.12 C.10 D.8
2.如图,已知中,,F是高和的交点,,,则线段的长度为( )
A. B.2 C. D.1
3.我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
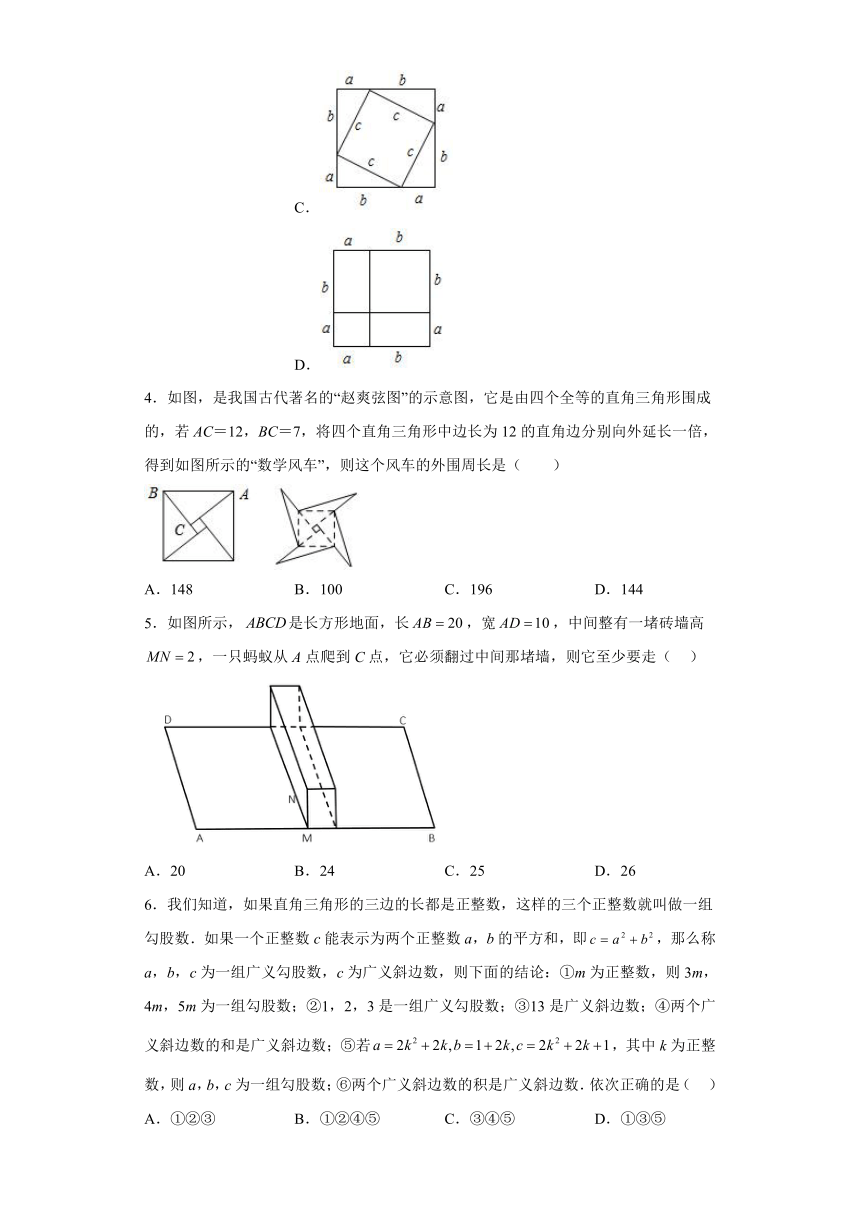
4.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
5.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
6.我们知道,如果直角三角形的三边的长都是正整数,这样的三个正整数就叫做一组勾股数.如果一个正整数c能表示为两个正整数a,b的平方和,即,那么称a,b,c为一组广义勾股数,c为广义斜边数,则下面的结论:①m为正整数,则3m,4m,5m为一组勾股数;②1,2,3是一组广义勾股数;③13是广义斜边数;④两个广义斜边数的和是广义斜边数;⑤若,其中k为正整数,则a,b,c为一组勾股数;⑥两个广义斜边数的积是广义斜边数.依次正确的是( )
A.①②③ B.①②④⑤ C.③④⑤ D.①③⑤
7.为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米 B.1.2 米 C.1.25 米 D.1.5 米
8.如图,中,,将沿DE翻折,使点A与点B重合,则CE的长为( )
A. B.2 C. D.
9.的半径为,弦.若,则和的距离为( )
A. B. C.或 D.或
10.若的两边长,满足,则第三边的长是( )
A.5 B. C.5或7 D.5或
二、填空题
11.如图,和都是等腰直角三角形,若,,,则______.
12.如图,在中,,点D为的中点,将绕点D逆时针旋转得到,当点A的对应点落在边上时,点在的延长线上,连接,若,则的面积是____________.
13.一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦长20厘米,弓形高为2厘米,则镜面半径为____________厘米.
14.如图,在中,,将按如图方式折叠,使点B与点A重合,折痕为,则的长为________.
15.如图,某圆弧形拱桥的跨度AB=20m,拱高CD=5m,则该拱桥的半径为_______m.
三、解答题
16.在中,,于点D,于点E,连接.
(1)如图1,当为锐角三角形时,
①依题意补全图形,猜想与之间的数量关系并证明;
②用等式表示线段,,的数量关系,并证明.
(2)如图2,当为钝角时,直接写出线段,,的数量关系.
17.在平面直角坐标系xOy中,对于点A,规定点A的变换和变换.变换:将点A向左平移一个单位长度,再向上平移两个单位长度;变换:将点A向右平移三个单位长度,再向下平移一个单位长度
(1)若对点B进行变换,得到点(1,1),则对点B进行变换后得到的点的坐标为 .
(2)若对点C(m,0)进行变换得到点P,对点C(m,0)进行变换得到点Q,,求m的值.
(3)点D为y轴的正半轴上的一个定点,对点D进行变换后得到点E,点F为x轴上的一个动点,对点F进行变换之后得到点G,若的最小值为2,直接写出点D的坐标 .
18.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
19.如图,直线y=﹣x+4交x轴,y轴分别为A、B,点P为x轴上的一个动点,过点P作PG⊥直线AB于点G.
(1)求出点A、B的坐标,以及线段AB长.
(2)当点G与点B重合时,求△PAG的面积.
(3)连OG,当△POG为等腰三角形时,求点P的坐标.
参考答案:
1.C
2.D
3.D
4.A
5.D
6.D
7.A
8.D
9.C
10.D
11.26
12.
13.26
14.####1.75
15.12.5
16.(1)①图形见解析;猜想:, 理由见解析;②见解析;
(2)线段,,的数量关系:.
17.(1)(5,-2)
(2)
(3)(0,)
18.(1)见解析;(2)13
19.(1)A(3,0),B(0,4),AB=5
(2)
(3),或者
一、单选题
1.如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC上有一点D,且,.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.
A.14 B.12 C.10 D.8
2.如图,已知中,,F是高和的交点,,,则线段的长度为( )
A. B.2 C. D.1
3.我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
4.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
5.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
6.我们知道,如果直角三角形的三边的长都是正整数,这样的三个正整数就叫做一组勾股数.如果一个正整数c能表示为两个正整数a,b的平方和,即,那么称a,b,c为一组广义勾股数,c为广义斜边数,则下面的结论:①m为正整数,则3m,4m,5m为一组勾股数;②1,2,3是一组广义勾股数;③13是广义斜边数;④两个广义斜边数的和是广义斜边数;⑤若,其中k为正整数,则a,b,c为一组勾股数;⑥两个广义斜边数的积是广义斜边数.依次正确的是( )
A.①②③ B.①②④⑤ C.③④⑤ D.①③⑤
7.为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米 B.1.2 米 C.1.25 米 D.1.5 米
8.如图,中,,将沿DE翻折,使点A与点B重合,则CE的长为( )
A. B.2 C. D.
9.的半径为,弦.若,则和的距离为( )
A. B. C.或 D.或
10.若的两边长,满足,则第三边的长是( )
A.5 B. C.5或7 D.5或
二、填空题
11.如图,和都是等腰直角三角形,若,,,则______.
12.如图,在中,,点D为的中点,将绕点D逆时针旋转得到,当点A的对应点落在边上时,点在的延长线上,连接,若,则的面积是____________.
13.一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦长20厘米,弓形高为2厘米,则镜面半径为____________厘米.
14.如图,在中,,将按如图方式折叠,使点B与点A重合,折痕为,则的长为________.
15.如图,某圆弧形拱桥的跨度AB=20m,拱高CD=5m,则该拱桥的半径为_______m.
三、解答题
16.在中,,于点D,于点E,连接.
(1)如图1,当为锐角三角形时,
①依题意补全图形,猜想与之间的数量关系并证明;
②用等式表示线段,,的数量关系,并证明.
(2)如图2,当为钝角时,直接写出线段,,的数量关系.
17.在平面直角坐标系xOy中,对于点A,规定点A的变换和变换.变换:将点A向左平移一个单位长度,再向上平移两个单位长度;变换:将点A向右平移三个单位长度,再向下平移一个单位长度
(1)若对点B进行变换,得到点(1,1),则对点B进行变换后得到的点的坐标为 .
(2)若对点C(m,0)进行变换得到点P,对点C(m,0)进行变换得到点Q,,求m的值.
(3)点D为y轴的正半轴上的一个定点,对点D进行变换后得到点E,点F为x轴上的一个动点,对点F进行变换之后得到点G,若的最小值为2,直接写出点D的坐标 .
18.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
19.如图,直线y=﹣x+4交x轴,y轴分别为A、B,点P为x轴上的一个动点,过点P作PG⊥直线AB于点G.
(1)求出点A、B的坐标,以及线段AB长.
(2)当点G与点B重合时,求△PAG的面积.
(3)连OG,当△POG为等腰三角形时,求点P的坐标.
参考答案:
1.C
2.D
3.D
4.A
5.D
6.D
7.A
8.D
9.C
10.D
11.26
12.
13.26
14.####1.75
15.12.5
16.(1)①图形见解析;猜想:, 理由见解析;②见解析;
(2)线段,,的数量关系:.
17.(1)(5,-2)
(2)
(3)(0,)
18.(1)见解析;(2)13
19.(1)A(3,0),B(0,4),AB=5
(2)
(3),或者
