2022-2023学年人教版八年级数学下册第18章 平行四边形 单元综合能力提升测试卷(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册第18章 平行四边形 单元综合能力提升测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览


文档简介
2022-2023学年新人教版初中八年级数学下册
第18单元综合能力提升测试卷
时间:90分钟 满分:120分
班级__________姓名__________得分__________
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)已知在 ABCD中,∠B+∠D=200°,则∠B的度数为( )
A.100° B.160° C.80° D.60°
2.(3分)如图,点O为矩形ABCD的对角线AC的中点,OP∥AB交BC于点P,连接OD,若OP=3,AD=8,则OD的长为( )
A.3 B.4 C.5 D.6
3.(3分)如图,在矩形ABCD中,AC、BD交于点O,E为BC边上一点,若BC=8,BO=5,EC=3,则OE的长为( )
A.2 B.4 C. D.3
4.(3分)菱形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相垂直
C.对角相等 D.对边平行
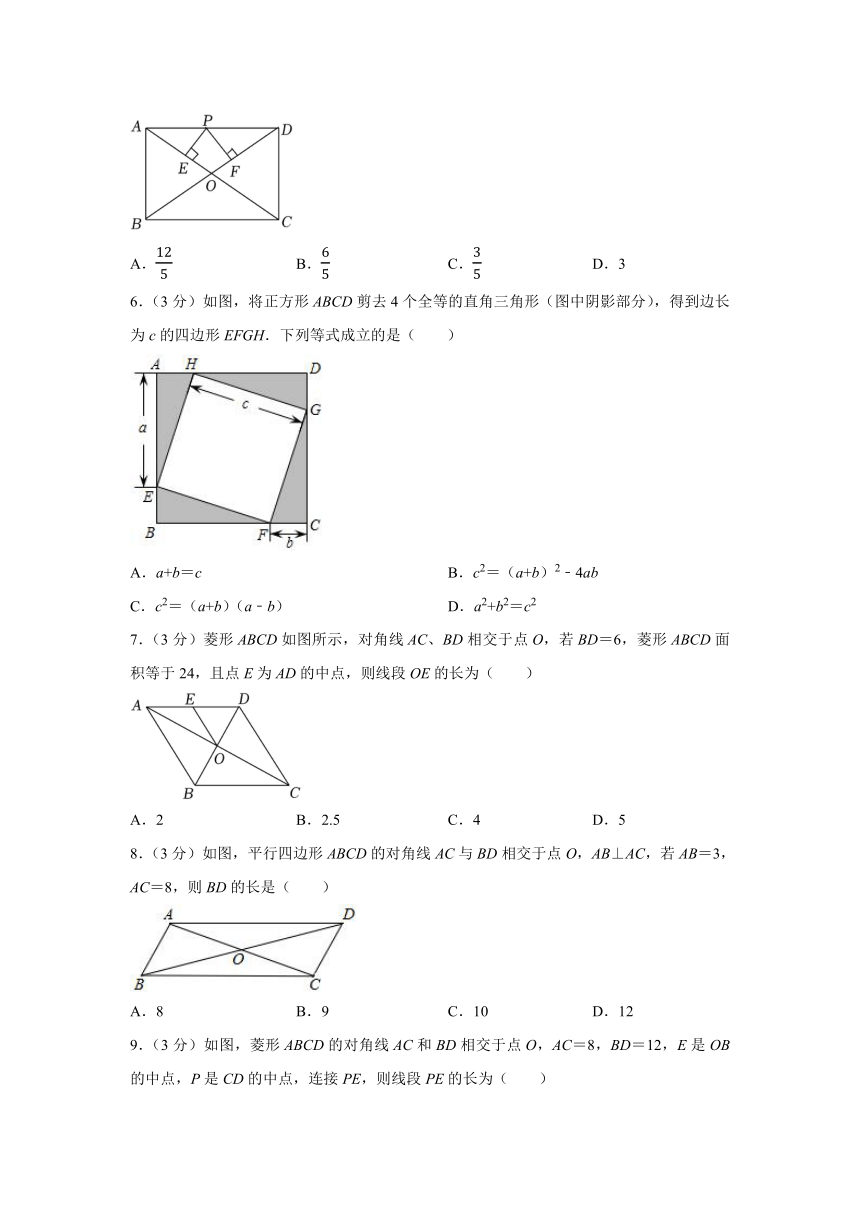
5.(3分)如图,在矩形ABCD中,AB=3,AD=4,对角线AC、BD相交于点O,点P是AD上一动点(不与A、D重合),过点P作AC和BD的垂线,垂足分别为E、F,则PE+PF的值是( )
A. B. C. D.3
6.(3分)如图,将正方形ABCD剪去4个全等的直角三角形(图中阴影部分),得到边长为c的四边形EFGH.下列等式成立的是( )
A.a+b=c B.c2=(a+b)2﹣4ab
C.c2=(a+b)(a﹣b) D.a2+b2=c2
7.(3分)菱形ABCD如图所示,对角线AC、BD相交于点O,若BD=6,菱形ABCD面积等于24,且点E为AD的中点,则线段OE的长为( )
A.2 B.2.5 C.4 D.5
8.(3分)如图,平行四边形ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=3,AC=8,则BD的长是( )
A.8 B.9 C.10 D.12
9.(3分)如图,菱形ABCD的对角线AC和BD相交于点O,AC=8,BD=12,E是OB的中点,P是CD的中点,连接PE,则线段PE的长为( )
A. B. C. D.
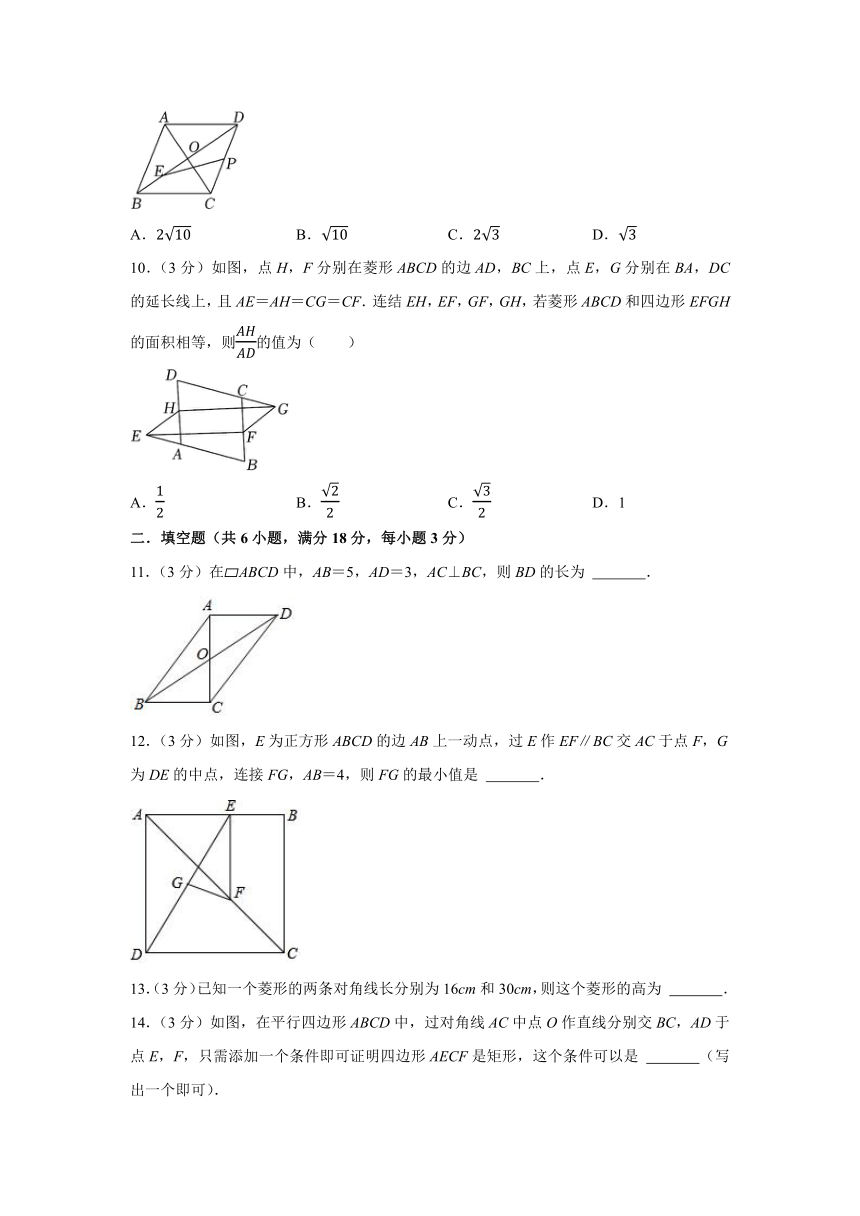
10.(3分)如图,点H,F分别在菱形ABCD的边AD,BC上,点E,G分别在BA,DC的延长线上,且AE=AH=CG=CF.连结EH,EF,GF,GH,若菱形ABCD和四边形EFGH的面积相等,则的值为( )
A. B. C. D.1
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)在 ABCD中,AB=5,AD=3,AC⊥BC,则BD的长为 .
12.(3分)如图,E为正方形ABCD的边AB上一动点,过E作EF∥BC交AC于点F,G为DE的中点,连接FG,AB=4,则FG的最小值是 .
13.(3分)已知一个菱形的两条对角线长分别为16cm和30cm,则这个菱形的高为 .
14.(3分)如图,在平行四边形ABCD中,过对角线AC中点O作直线分别交BC,AD于点E,F,只需添加一个条件即可证明四边形AECF是矩形,这个条件可以是 (写出一个即可).
15.(3分)如图,过△ABC的边AB,AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高.延长HA交EG于点I.若S△AEG=7,则S△AEI= .
16.(3分)如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=35°,则∠OBC的大小为 度.
三.解答题(共10小题,满分72分)
17.(5分)如图,已知ABCD是正方形,点E是BC的中点,连接AE,过B作BO⊥AE于O,延长BO交CD于F.
求证:F是CD的中点.
18.(5分)如图所示,已知四边形ABCD是平行四边形,AD=3,CD=5,若AF,BE分别是∠DAB,∠CBA的平分线.求EF的长.
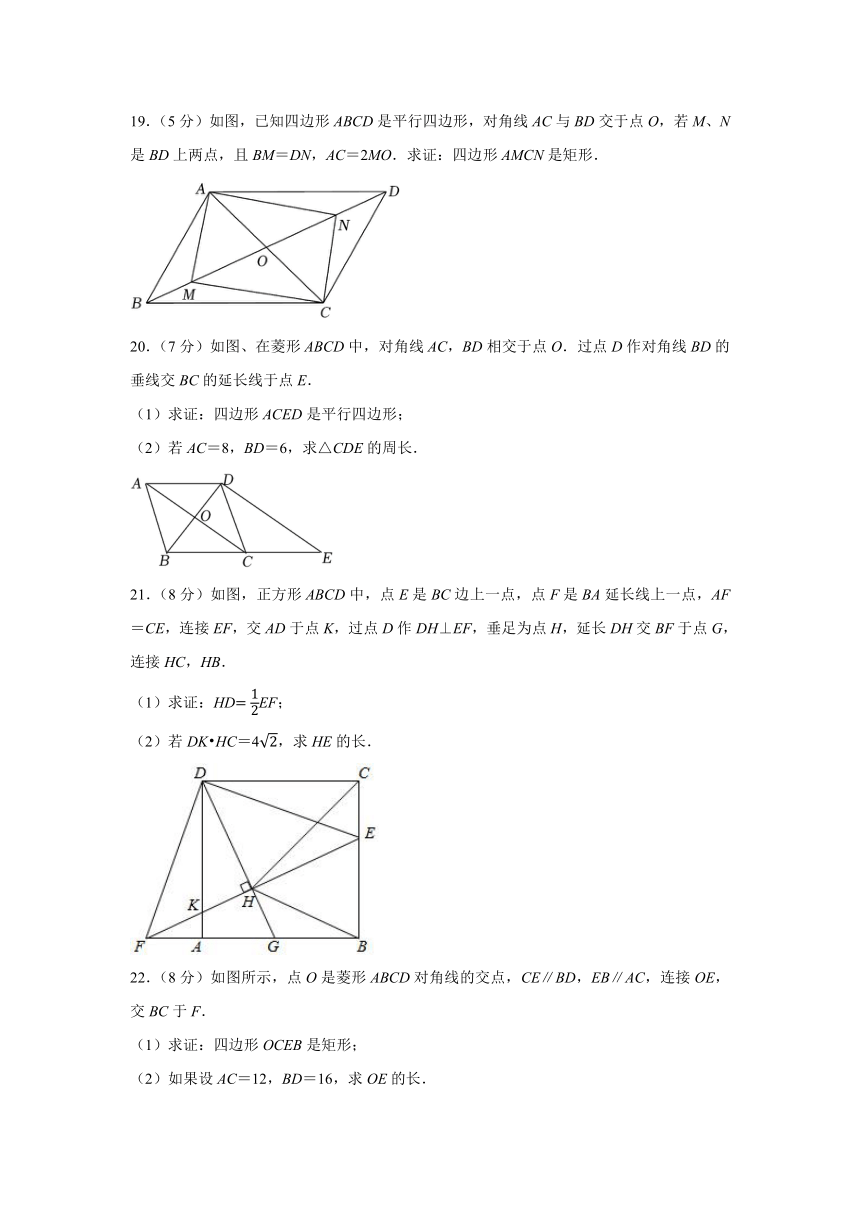
19.(5分)如图,已知四边形ABCD是平行四边形,对角线AC与BD交于点O,若M、N是BD上两点,且BM=DN,AC=2MO.求证:四边形AMCN是矩形.
20.(7分)如图、在菱形ABCD中,对角线AC,BD相交于点O.过点D作对角线BD的垂线交BC的延长线于点E.
(1)求证:四边形ACED是平行四边形;
(2)若AC=8,BD=6,求△CDE的周长.
21.(8分)如图,正方形ABCD中,点E是BC边上一点,点F是BA延长线上一点,AF=CE,连接EF,交AD于点K,过点D作DH⊥EF,垂足为点H,延长DH交BF于点G,连接HC,HB.
(1)求证:HDEF;
(2)若DK HC=4,求HE的长.
22.(8分)如图所示,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
(1)求证:四边形OCEB是矩形;
(2)如果设AC=12,BD=16,求OE的长.
23.(8分)如图,矩形ABCD,延长CD至点E,使DE=CD,连接AC,AE,过点C作CF∥AE交AD的延长线于点F,连接EF.
(1)求证:四边形ACFE是菱形;
(2)连接BE交AD于点G.当AB=1,∠ACB=30°时,求BG的长.
24.(8分)如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,,求AB的长.
25.(8分)如图,在△ABC中,D是AC边上一点,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)如果BD是△ABC的角平分线,求证:四边形BEDF是菱形.
(2)如果BD是△ABC的中线且AC=2BD,请判断四边形BEDF的形状并说明理由.
26.(10分)如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
参考答案
1.A; 2.C; 3.C; 4.B; 5.A; 6.D; 7.B; 8.C; 9.A; 10.D;
11.;
12.;
13.cm;
14.∠AEC=90°(答案不唯一);
15.3.5;
16.55;
17.证明:∵点E是BC的中点,
∴BE=EC,
∵BO⊥AE,
∴∠AEB+∠FBC=90°=∠AEB+∠BAE,
∴∠BAE=∠FBC,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(ASA),
∴CF=BEBCCD,
∴点F是CD的中点.
18.解:∵AB∥CD,
∴∠DFA=∠FAB,
∵AF、BE分别是∠DAB,∠CBA的平分线,
∴∠DAF=∠FAB,
∴∠DAF=∠DFA,
∴DA=DF,
同理得出CE=CB,
∴DF=EC,
∵AD=3,
∴DF=3,
同理:CE=3,
∵AB=DC=5
∴EF=DF+EC﹣DC=2BC﹣DC=3+3﹣5=1.
19.证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵MO=NO,
∴MN=2MO,
∵AC=2MO,
∴MN=AC,
∴四边形AMCN是矩形.
20.(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∵DE⊥BD,
∴DE∥AC,
∴四边形ACDE是平行四边形;
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AOAC=4,DOBD=3,AC⊥BD,
∴∠AOD=90°,
∴CD=AD5,
由(1)得:四边形ACDE是平行四边形,
∴CE=AD=5,DE=AC=12,
∴△CDE的周长=AD+AE+DE=5+5+8=18.
21.(1)证明:∵四边形ABCD为正方形,
∴CD=AD,∠DCE=∠DAF=90°,
∵CE=AF,
∴△DCE≌△DAF(SAS);
∴DE=DF,∠CDE=∠ADF,
∴∠FDE=∠ADF+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴△DFE为等腰直角三角形,
∵DH⊥EF,
∴点H是EF的中点,
∴DHEF;
(2)解:∵四边形ABCD为正方形,
∴CD=CB,
∵点H是EF的中点,∠ABC=90°,
∴HBEF,
∴DH=HB,
又∵CH=CH,
∴△DCH≌△BCH(SSS),
∴∠DCH=∠BCH=45°,
∵△DEF为等腰直角三角形,
∴∠DFE=45°,
∴∠HCE=∠DFK,
∵四边形ABCD为正方形,
∴AD∥BC,
∴∠DKF=∠HEC,
∴△DKF∽△HEC,
∴,
∴DK HC=DF HE,
在等腰直角三角形DFH中,DFHFHE,
∴DK HC=DF HEHE2=4,
∴HE=2.
22.(1)证明:∵CE∥BD,EB∥AC,
∴四边形OBEC为平行四边形.
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠BOC=90°,
∴四边形OBEC为矩形;
(2)解:∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OCAC=6,OB=ODBD=8,
∴∠DOC=90°,CD10,
∵平行四边形OCED为矩形,
∴OE=CD=10.
23.(1)证明:∵四边形ABCD是矩形,
∴∠ADC=90°,
∴AF⊥CE,
∵CD=DE,
∴AE=AC,EF=CF,
∴∠EAD=∠CAD,
∵AE∥CF,
∴∠EAD=∠AFC,
∴∠CAD=∠CFA,
∴AC=CF,
∴AE=EF=AC=CF,
∴四边形ACFE是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠ABC=∠BCE=90°,CD=AB,
∵AB=1,DE=CD=1,
∵∠ACB=30°,
∴AC=2AB=2,
∴BC,CE=2,
∴BE,
∵AB=CD=DE,∠BAG=∠EDG=90°,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴BG=EG,
∴BGBE.
24.(1)证明:∵AB∥CE,
∴∠CAD=∠ACE,∠ADE=∠CED.
∵F是AC中点,
∴AF=CF.
在△AFD与△CFE中,
.
∴△AFD≌△CFE(AAS),
∴DF=EF,
∴四边形ADCE是平行四边形;
(2)解:过点C作CG⊥AB于点G.
在△ACG中,∠AGC=90°,AC,∠CAG=45°,
∴由勾股定理得CG=AG=1.
在△BCG中,∠BGC=90°,∠B=30°,CG=1,
∴BC=2,
∴BG,
∴AB=AG+BG.
25.(1)证明:∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF,
∴∠ABD=∠EDB,
∴DE=BE,
∴平行四边形BEDF是菱形;
(2)解:四边形BEDF是矩形,理由如下:
∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∵BD是△ABC的中线,
∴AD=CDAC,
∵AC=2BD,
∴AD=CD=BD,
∴∠BAC=∠ABD,∠BCA=∠CBD,
∵∠BAC+∠ABD+∠BCA+∠CBD=180°,即2∠ABD+2∠CBD=180°,
∴∠ABD+∠CBD=90°,即∠ABC=90°,
∴平行四边形BEDF是矩形.
26.(1)证明:如图1,∵AM是△ABC的中线,D与M重合,
∴DC=BD,
∵DE∥AB,
∴∠EDC=∠B,
∵CE∥AM,即CE∥AD,
∴∠ECD=∠ADB,
在△ECD和△ADB中,
,
∴△ECD≌△ADB(ASA),
∴DE=AB,
∴四边形ABDE是平行四边形.
(2)成立,理由如下:
如图2,过点M作MG∥AB交CG于点G,
∵DE∥AB,
∴MG∥DE,
∵CE∥AM,
∴四边形DEGM是平行四边形,
∴MG=DE,
由(1)得MG=AB,
∴DE=AB,
∴四边形ABDE是平行四边形.
第18单元综合能力提升测试卷
时间:90分钟 满分:120分
班级__________姓名__________得分__________
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)已知在 ABCD中,∠B+∠D=200°,则∠B的度数为( )
A.100° B.160° C.80° D.60°
2.(3分)如图,点O为矩形ABCD的对角线AC的中点,OP∥AB交BC于点P,连接OD,若OP=3,AD=8,则OD的长为( )
A.3 B.4 C.5 D.6
3.(3分)如图,在矩形ABCD中,AC、BD交于点O,E为BC边上一点,若BC=8,BO=5,EC=3,则OE的长为( )
A.2 B.4 C. D.3
4.(3分)菱形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相垂直
C.对角相等 D.对边平行
5.(3分)如图,在矩形ABCD中,AB=3,AD=4,对角线AC、BD相交于点O,点P是AD上一动点(不与A、D重合),过点P作AC和BD的垂线,垂足分别为E、F,则PE+PF的值是( )
A. B. C. D.3
6.(3分)如图,将正方形ABCD剪去4个全等的直角三角形(图中阴影部分),得到边长为c的四边形EFGH.下列等式成立的是( )
A.a+b=c B.c2=(a+b)2﹣4ab
C.c2=(a+b)(a﹣b) D.a2+b2=c2
7.(3分)菱形ABCD如图所示,对角线AC、BD相交于点O,若BD=6,菱形ABCD面积等于24,且点E为AD的中点,则线段OE的长为( )
A.2 B.2.5 C.4 D.5
8.(3分)如图,平行四边形ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=3,AC=8,则BD的长是( )
A.8 B.9 C.10 D.12
9.(3分)如图,菱形ABCD的对角线AC和BD相交于点O,AC=8,BD=12,E是OB的中点,P是CD的中点,连接PE,则线段PE的长为( )
A. B. C. D.
10.(3分)如图,点H,F分别在菱形ABCD的边AD,BC上,点E,G分别在BA,DC的延长线上,且AE=AH=CG=CF.连结EH,EF,GF,GH,若菱形ABCD和四边形EFGH的面积相等,则的值为( )
A. B. C. D.1
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)在 ABCD中,AB=5,AD=3,AC⊥BC,则BD的长为 .
12.(3分)如图,E为正方形ABCD的边AB上一动点,过E作EF∥BC交AC于点F,G为DE的中点,连接FG,AB=4,则FG的最小值是 .
13.(3分)已知一个菱形的两条对角线长分别为16cm和30cm,则这个菱形的高为 .
14.(3分)如图,在平行四边形ABCD中,过对角线AC中点O作直线分别交BC,AD于点E,F,只需添加一个条件即可证明四边形AECF是矩形,这个条件可以是 (写出一个即可).
15.(3分)如图,过△ABC的边AB,AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高.延长HA交EG于点I.若S△AEG=7,则S△AEI= .
16.(3分)如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=35°,则∠OBC的大小为 度.
三.解答题(共10小题,满分72分)
17.(5分)如图,已知ABCD是正方形,点E是BC的中点,连接AE,过B作BO⊥AE于O,延长BO交CD于F.
求证:F是CD的中点.
18.(5分)如图所示,已知四边形ABCD是平行四边形,AD=3,CD=5,若AF,BE分别是∠DAB,∠CBA的平分线.求EF的长.
19.(5分)如图,已知四边形ABCD是平行四边形,对角线AC与BD交于点O,若M、N是BD上两点,且BM=DN,AC=2MO.求证:四边形AMCN是矩形.
20.(7分)如图、在菱形ABCD中,对角线AC,BD相交于点O.过点D作对角线BD的垂线交BC的延长线于点E.
(1)求证:四边形ACED是平行四边形;
(2)若AC=8,BD=6,求△CDE的周长.
21.(8分)如图,正方形ABCD中,点E是BC边上一点,点F是BA延长线上一点,AF=CE,连接EF,交AD于点K,过点D作DH⊥EF,垂足为点H,延长DH交BF于点G,连接HC,HB.
(1)求证:HDEF;
(2)若DK HC=4,求HE的长.
22.(8分)如图所示,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
(1)求证:四边形OCEB是矩形;
(2)如果设AC=12,BD=16,求OE的长.
23.(8分)如图,矩形ABCD,延长CD至点E,使DE=CD,连接AC,AE,过点C作CF∥AE交AD的延长线于点F,连接EF.
(1)求证:四边形ACFE是菱形;
(2)连接BE交AD于点G.当AB=1,∠ACB=30°时,求BG的长.
24.(8分)如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,,求AB的长.
25.(8分)如图,在△ABC中,D是AC边上一点,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)如果BD是△ABC的角平分线,求证:四边形BEDF是菱形.
(2)如果BD是△ABC的中线且AC=2BD,请判断四边形BEDF的形状并说明理由.
26.(10分)如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
参考答案
1.A; 2.C; 3.C; 4.B; 5.A; 6.D; 7.B; 8.C; 9.A; 10.D;
11.;
12.;
13.cm;
14.∠AEC=90°(答案不唯一);
15.3.5;
16.55;
17.证明:∵点E是BC的中点,
∴BE=EC,
∵BO⊥AE,
∴∠AEB+∠FBC=90°=∠AEB+∠BAE,
∴∠BAE=∠FBC,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(ASA),
∴CF=BEBCCD,
∴点F是CD的中点.
18.解:∵AB∥CD,
∴∠DFA=∠FAB,
∵AF、BE分别是∠DAB,∠CBA的平分线,
∴∠DAF=∠FAB,
∴∠DAF=∠DFA,
∴DA=DF,
同理得出CE=CB,
∴DF=EC,
∵AD=3,
∴DF=3,
同理:CE=3,
∵AB=DC=5
∴EF=DF+EC﹣DC=2BC﹣DC=3+3﹣5=1.
19.证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵MO=NO,
∴MN=2MO,
∵AC=2MO,
∴MN=AC,
∴四边形AMCN是矩形.
20.(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∵DE⊥BD,
∴DE∥AC,
∴四边形ACDE是平行四边形;
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AOAC=4,DOBD=3,AC⊥BD,
∴∠AOD=90°,
∴CD=AD5,
由(1)得:四边形ACDE是平行四边形,
∴CE=AD=5,DE=AC=12,
∴△CDE的周长=AD+AE+DE=5+5+8=18.
21.(1)证明:∵四边形ABCD为正方形,
∴CD=AD,∠DCE=∠DAF=90°,
∵CE=AF,
∴△DCE≌△DAF(SAS);
∴DE=DF,∠CDE=∠ADF,
∴∠FDE=∠ADF+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴△DFE为等腰直角三角形,
∵DH⊥EF,
∴点H是EF的中点,
∴DHEF;
(2)解:∵四边形ABCD为正方形,
∴CD=CB,
∵点H是EF的中点,∠ABC=90°,
∴HBEF,
∴DH=HB,
又∵CH=CH,
∴△DCH≌△BCH(SSS),
∴∠DCH=∠BCH=45°,
∵△DEF为等腰直角三角形,
∴∠DFE=45°,
∴∠HCE=∠DFK,
∵四边形ABCD为正方形,
∴AD∥BC,
∴∠DKF=∠HEC,
∴△DKF∽△HEC,
∴,
∴DK HC=DF HE,
在等腰直角三角形DFH中,DFHFHE,
∴DK HC=DF HEHE2=4,
∴HE=2.
22.(1)证明:∵CE∥BD,EB∥AC,
∴四边形OBEC为平行四边形.
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠BOC=90°,
∴四边形OBEC为矩形;
(2)解:∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OCAC=6,OB=ODBD=8,
∴∠DOC=90°,CD10,
∵平行四边形OCED为矩形,
∴OE=CD=10.
23.(1)证明:∵四边形ABCD是矩形,
∴∠ADC=90°,
∴AF⊥CE,
∵CD=DE,
∴AE=AC,EF=CF,
∴∠EAD=∠CAD,
∵AE∥CF,
∴∠EAD=∠AFC,
∴∠CAD=∠CFA,
∴AC=CF,
∴AE=EF=AC=CF,
∴四边形ACFE是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠ABC=∠BCE=90°,CD=AB,
∵AB=1,DE=CD=1,
∵∠ACB=30°,
∴AC=2AB=2,
∴BC,CE=2,
∴BE,
∵AB=CD=DE,∠BAG=∠EDG=90°,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴BG=EG,
∴BGBE.
24.(1)证明:∵AB∥CE,
∴∠CAD=∠ACE,∠ADE=∠CED.
∵F是AC中点,
∴AF=CF.
在△AFD与△CFE中,
.
∴△AFD≌△CFE(AAS),
∴DF=EF,
∴四边形ADCE是平行四边形;
(2)解:过点C作CG⊥AB于点G.
在△ACG中,∠AGC=90°,AC,∠CAG=45°,
∴由勾股定理得CG=AG=1.
在△BCG中,∠BGC=90°,∠B=30°,CG=1,
∴BC=2,
∴BG,
∴AB=AG+BG.
25.(1)证明:∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF,
∴∠ABD=∠EDB,
∴DE=BE,
∴平行四边形BEDF是菱形;
(2)解:四边形BEDF是矩形,理由如下:
∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∵BD是△ABC的中线,
∴AD=CDAC,
∵AC=2BD,
∴AD=CD=BD,
∴∠BAC=∠ABD,∠BCA=∠CBD,
∵∠BAC+∠ABD+∠BCA+∠CBD=180°,即2∠ABD+2∠CBD=180°,
∴∠ABD+∠CBD=90°,即∠ABC=90°,
∴平行四边形BEDF是矩形.
26.(1)证明:如图1,∵AM是△ABC的中线,D与M重合,
∴DC=BD,
∵DE∥AB,
∴∠EDC=∠B,
∵CE∥AM,即CE∥AD,
∴∠ECD=∠ADB,
在△ECD和△ADB中,
,
∴△ECD≌△ADB(ASA),
∴DE=AB,
∴四边形ABDE是平行四边形.
(2)成立,理由如下:
如图2,过点M作MG∥AB交CG于点G,
∵DE∥AB,
∴MG∥DE,
∵CE∥AM,
∴四边形DEGM是平行四边形,
∴MG=DE,
由(1)得MG=AB,
∴DE=AB,
∴四边形ABDE是平行四边形.
