第二十章 数据的分析 单元学习质量检测卷(含答案) 2022-2023学年人教版八年级数学下册
文档属性
| 名称 | 第二十章 数据的分析 单元学习质量检测卷(含答案) 2022-2023学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 471.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览




文档简介
2022-2023学年新人教版初中数学八年级下册
第二十单元学习质量检测卷
时间:120分钟 满分:120分
班级__________姓名__________得分__________
一、选择题(共10小题,满分30分,每小题3分)
1.(3分)全国文明典范城市是全国文明城市的升级版,也是文明城市的标杆.2021年,长沙市抬高创建坐标,全力以赴推进“全国文明城市”向“全国文明典范城市”迭代升级.12月25日,长沙市文明办组织开展“长沙文明十二点”网络征集广纳建言活动,面向社会各界广泛征求意见和建议.芙蓉区某中学的小亮响应号召,对自己居住小区家庭使用垃圾袋的情况进行了调查,小亮随机调查了小区10户家庭一周垃圾袋的使用量,结果如下(单位:个),7,7,8,8,9,9,10,11,14,关于这组数据下列结论正确的是
A.平均数是10 B.众数是7 C.中位数是8 D.极差是6
2.(3分)为了增强学生的安全意识,某校组织学生开展了安全知识竟赛活动,经过一轮初赛后,共有21人进入决赛,本次活动将按照决赛分数评出一等奖2名,二等奖3名,三等奖5名.小丽进入了决寨,要判断自己能否获奖,她应当关注决赛分数的
A.平均数 B.众数 C.中位数 D.方差
3.(3分)描述一组数据的离散程度,我们还可以用“平均差”.在一组数、、、、中,各数据与它们的平均数的差的绝对值的平均数,即叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大,稳定性越小.现有甲、乙两组数据,如表所示,则下列说法错误的是
甲 12 13 11 15 13 14
乙 10 16 10 18 17 7
A.甲、乙两组数据的平均数相同
B.乙组数据的平均差为4
C.甲组数据的平均差是2
D.甲组数据更加稳定
4.(3分)在一次数学测验中,甲、乙、丙、丁四位同学的成绩(单位:分)分别是80,,80,70,若这四位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是
A.90分 B.85分 C.80分 D.75分
5.(3分)某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙、丁的成绩分析如表所示:
甲 乙 丙 丁
平均数 7.9 7.9 8.0 8.0
方差 3.29 0.49 1.8 0.4
根据以上图表信息,参赛选手应选
A.甲 B.乙 C.丙 D.丁
6.(3分)某校九年级(3)班全体学生2021年中考体育模拟考试的成绩统计如下表:
成绩(分 36 40 43 46 48 50 54
人数(人 2 5 6 7 8 7 5
根据上表中的信息判断,下列结论中错误的是
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是48分
C.该班学生这次考试成绩的中位数是47分
D.该班学生这次考试成绩的平均数是46分
7.(3分)根据某市统计局发布的该市近5年的年度增长率的有关数据,经济学家评论说,该市近5年的年度增长率相当平稳,从统计学的角度看,“增长率相当平稳”说明这组数据的 比较小.
A.中位数 B.平均数 C.众数 D.方差
8.(3分)对于一组数据,,4,2,下列结论不正确的是
A.平均数是1 B.方差是3.5 C.中位数是0.5 D.众数是
9.(3分)某组数据方差计算公式为:,由公式提供的信息,下列说法错误的是
A.样本的容量是3 B.样本的中位数是3
C.样本的众数是3 D.样本的平均数是3
10.(3分)某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是
A.50,48 B.48,49 C.50,49 D.48,48
二、填空题(共5小题,满分15分,每小题3分)
11.(3分)若一组数据2,3,4,5,的方差与另一组数据5,6,7,8,9的方差相等,则 .
12.(3分)某班有50人,一次数学测试后,老师对测试成绩进行了统计.由于小颖没有参加此次集体测试,因此计算其他49人的平均分为92分,方差.后来小颖进行了补测,成绩是92分,则该班50人的数学测试成绩的方差 (填“变小”、“不变”、“变大” .
13.(3分)已知一组数据,,,,的平均数是2,方差是5,那么另一组数据,,,,的平均数和方差的和为 .
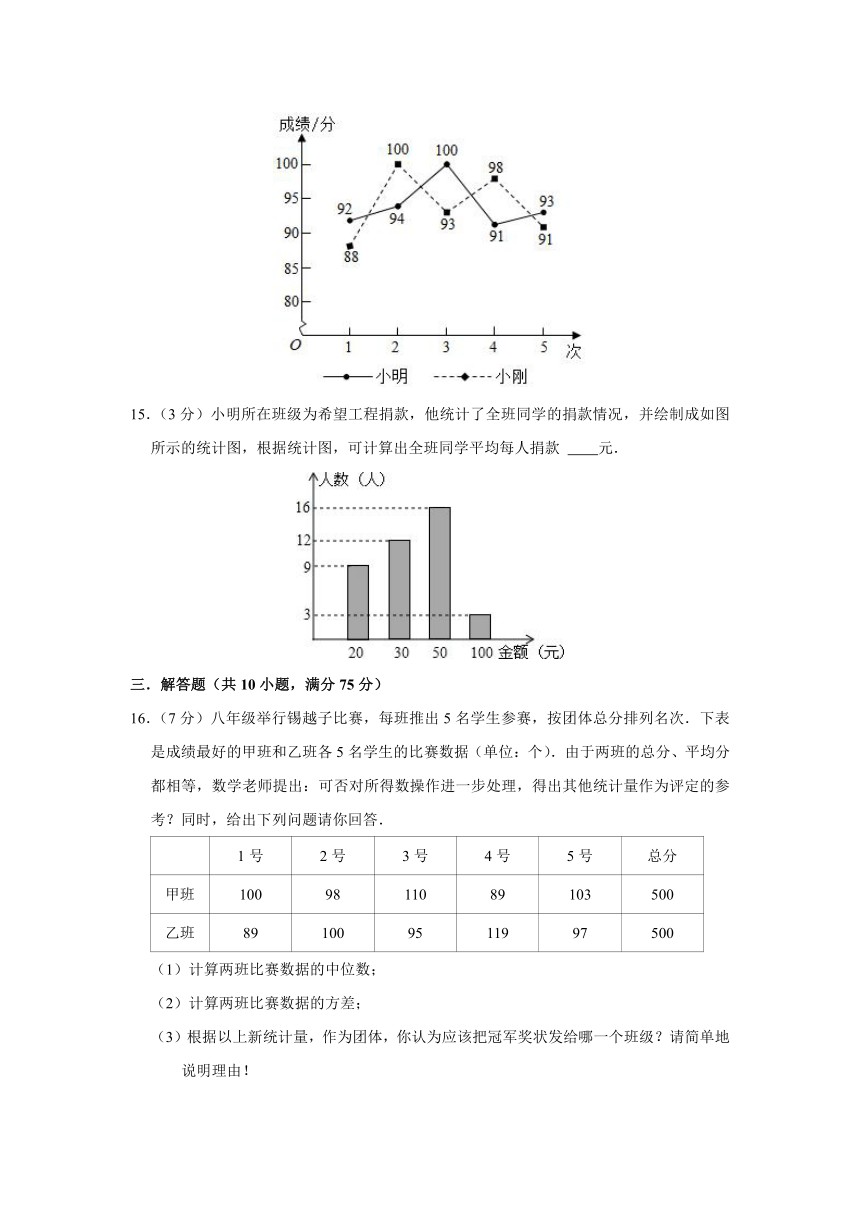
14.(3分)为庆祝中国共产党建党100周年,某商校组织党史知识竞赛,根据小明、小刚5次预赛成绩绘制成统计图,下面三个推断:
①与小刚相比,小明5次成绩的极差大;
②与小刚相比,小明5次成绩的平均数大;
③与小刚相比,小明5次成绩的方差小;
④与小刚相比,小明的成绩比较稳定.
其中,所有合理推断的序号是 .
15.(3分)小明所在班级为希望工程捐款,他统计了全班同学的捐款情况,并绘制成如图所示的统计图,根据统计图,可计算出全班同学平均每人捐款 元.
三.解答题(共10小题,满分75分)
16.(7分)八年级举行锡越子比赛,每班推出5名学生参赛,按团体总分排列名次.下表是成绩最好的甲班和乙班各5名学生的比赛数据(单位:个).由于两班的总分、平均分都相等,数学老师提出:可否对所得数操作进一步处理,得出其他统计量作为评定的参考?同时,给出下列问题请你回答.
1号 2号 3号 4号 5号 总分
甲班 100 98 110 89 103 500
乙班 89 100 95 119 97 500
(1)计算两班比赛数据的中位数;
(2)计算两班比赛数据的方差;
(3)根据以上新统计量,作为团体,你认为应该把冠军奖状发给哪一个班级?请简单地说明理由!
17.(7分)某车间有工人10人,某月他们生产的零件个数统计如下表:
生产零件的个数(个) 600 480 220 180 120
工人人数(人) 1 1 3 4 1
(1)求这10名工人该月生产零件的平均个数;
(2)为了调动工人的积极性,决定实行目标管理,对完成目标的工人进行适当的奖励.如果想让一半左右的工人都能获得奖励,请你从平均数、中位数、众数的角度进行分析,该如何确定月生产目标?
18.(7分)农业农村经济在国民经济中占有重要地位,科技兴农、为促进乡村产业振兴提供有力支撑.为了解甲、乙两种新品猕猴桃的质量,进行了抽样调查.在相同条件下,随机抽取了甲、乙各25份样品,对大小、甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.
.测评分数(百分制)如下:
甲 77 79 80 80 85 86 86 87 88 89 89 90 91 91 91 91 91 92 93 95 95 96 97 98 98
乙 69 87 79 79 8679 87 89 90 89 90 90 90 91 90 92 92 94 92 95 96 96 97 98 98
.按如下分组整理、描述这两组样本数据:
测评分数 个数 品种
甲 0 9 14
乙 1 3 16
注:分数90分及以上为优秀,分为合格,80分以下为不合格.
.甲、乙两种猕猴桃测评分数的平均数、众数、中位数如表所示:
品种 平均数 众数 中位数
甲 89.4 91
乙 89.4 90
根据以上信息,回答下列问题:
(1)写出表中,,,的值;
(2)记甲种猕猴桃测评分数的方差为,乙种猕猴桃测评分数的方差为,则,的大小关系为 ;
(3)根据抽样调查情况,可以推断 种猕猴桃的质量较好,理由为 .(至少从两个不同的角度说明推断的合理性)
19.(7分)为进一步宣传防震减灾科普知识,增强学生应急避险和自救互救能力,某校组织七、八年级各200名学生进行“防震减灾知识测试”(满分100分).现分别在七、八年级中各随机抽取10名学生的测试成绩(单位:分)进行统计、整理如下:
七年级:86,90,79,84,74,93,76,81,90,87.
八年级:85,76,90,81,84,92,81,84,83,84
七八年级测试成绩频数统计表
七年级 3 4 3
八年级 1 7
七八年级测试成绩分析统计表
平均数 中位数 众数 方差
七年级 84 90 36.4
八年级 84 84 8.4
根据以上信息,解答下列问题:
(1) , , .
(2)规定分数不低于85分记为“优秀”,估计这两个年级测试成绩达到“优秀”的学生人数.
(3)你认为哪个年级的学生掌握防震减灾科普知识的总体水平较好?请说明理由.
20.(7分)随着十九届六中全会的召开,中学生对时事新闻的关注度高涨.某校组织全校学生开展“时事新闻大比拼”比赛,并随机抽取九年级的25名学生的成绩(满分为100分)进行分析.收集数据:25名学生的成绩(满分为100分)统计如下(单位:分):
90,74,88,65,98,75,81,44,85,70,55,80,95,88,72,87,60,56,76,66,78,72,82,63,100
整理数据:
成绩(分)
人数 10 8
分析数据:
平均数 中位数 方差
76 190.88
(1)将表格中的数据补充完整(3个);
(2)“”这组数据的众数是 分;
(3)若全校九年级有800名学生,请估计全校九年级有多少名学生成绩达到90分及以上?
(4)若八年级成绩的平均数为76分,中位数为80分,方差为102.5,你认为哪个年级的成绩较好?请你做出评价.(至少从两个方面说明)
21.(8分)2021年底,西安突发新冠肺炎疫情、在各方共同努力下,取得了抗击疫情的阶段性胜利.日前,新一波新冠肺炎疫情又在中国香港地区蔓延,同时深圳、呼和浩特等多地也出现散发病例.做好新冠肺炎疫情防控时刻不能放松,对中学生来说抗击疫情的最好办法是强身健体,提高免疫力.某校为了解九年级学生周末在家体育银炼的情况,在该校九年级随机抽收了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了如下数据(单位:分钟):
【收集数据】
男生:28,30,32,39,46,57,58,66,68,69,70,70,80,88,95,99,100,105;
女生:29,35,36,48,55,56,62,69,69,72,73,78,88,88,90,98,99,109.
【整理数据】
锻炼时间
男生 1 7 4
女生 1 5 8 4
【分析数据】两组数据的平均数、中位数、众数如表:
统计量 组别 平均数 中位数 众数
男生 66.7 68.5
女生 69.7 69、88
根据以上信息解答下列问题:
(1)填空: , , ;
(2)如果该校九年级的男生有270人、女生有360人,估计该校九年级周末在家锻炼的时间在90分钟以上(不包含90分钟)同学的人数;
(3)王老师看了表格数据后认为九年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持王老师观点的理由.
22.(8分)为了落实立德树人根本任务,积极响应“双减”政策要求,某校开设了丰富的劳动教育课程.某日,学生处对学校菜圃耕作情况进行了一次评分.从七、八年级各随机抽取20块菜圃,对这部分菜圃的评分进行整理和分析(采圃评分均为整数,满分为10分,9分(含9分)以上为“五星菜圃”).相关数据统计、整理如下:
抽取八年级菜圃的评分(单位:分):
7,7,7,7,7,8,8,8,8,8,8,9,9,9,9,9,9,9,9,10.
七、八年级抽取的菜圃评分统计
年级 七年级 八年级
平均数 8.25 8.25
中位数 9
众数 9
方差 2.5875 0.7875
根据以上信息,解答下列问题:(1)填空: , ;
(2)该校七年级共19个班,每班有4块菜圃,估计该校七年级“五星菜圃”的数量;
(3)根据以上数据分析,从一个方面评价两个年级的菜圃耕种情况谁更好.
23.(8分)某校策划了一次有关党的知识竞赛,每班参加比赛的人数相同,成绩分为,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将九年级一班和二班的成绩进行整理并绘制成如下统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中,一班成绩在级以上(包括级)的人数为 人.
(2)请你根据平均数、众数、中位数等统计知识,综合阐述哪个班整体水平较高,可以评为一等奖?
24.(8分)我校为了提高学生的文明意识,举办了“文明知识”测评活动.现从九年级一班和二班中各随机抽取20名学生的测评成绩(满分50分,45分及45分以上为优秀,40分及40分以上为合格)进行整理、描述和分析,给出了下面的部分信息.
九年级一班20名学生的测评成绩(单位:分)分别为:
44 50 40 40 50 45 45 45 49 45 44 42 49 42 49 49 45 42 38 42
九年级二班20名学生的测评成绩统计图如图所示.
两个班抽取的学生的测评成绩的平均数、众数、中位数如表:
班级 平均数 众数 中位数
一班 44.75 45
二班 44.9
请你根据上面提供的所有信息,解容下列问题:
(1)表中的 , , .
(2)根据以上数据,你认为在此次测评中,九年级一班的测评成绩好还是九年级二班的测评成绩好?请说明理由(说明一条理由即可);
(3)已知学校九年级共800名学生参加了此次测评活动,通过计算,请你估计此次测评活动成绩合格的学生人数.
25.(8分)某中学开展“唱歌”比赛活动,八(1),八(2)班各选出5名选手参加复赛,5名选手的复赛成绩(满分为100分),如图所示:
(1)根据图示填写下表:
班级 中位数分 众数分
八(1)班 85
八(2)班 100
(2)通过计算得知八(2)的平均成绩为85分,请计算八(1)的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)经计算八(1)班复赛成绩的方差为70,请计算八(2)班复赛成绩的方差,并说明哪个班学生的成绩比较稳定.
参考答案
一、选择题(共10小题,满分30分,每小题3分)
1.B; 2.C; 3.C; 4.C; 5.D; 6.D; 7.D; 8.B; 9.A; 10.D;
二、填空题(共5小题,满分15分,每小题3分)
11.1或6;
12.变小;
13.49;
14.③④;
15.41;
三、解答题(共10小题,满分75分)
16.(1)甲班的中位数为100,乙班的中位数为98;
(2)甲班平均分为:,
;
乙班平均分为:,
乙班的方差为:;
(3)应该把冠军奖状发给甲班.
因为两班的平均分相同,但甲班的优秀率比乙班高,比赛数据的中位数也比乙班大,甲班比赛数据的方差比乙班小,说明甲班的成绩比乙班稳定,综合分析,甲班成绩好,所以应该把冠军奖状发给甲班.
17.(1)根据题意得:
(个).
答:这10名工人该月生产零件的平均个数为258个;
(2)共有10名工人,
中位数为(个),众数为180个,
当定额为258个时,有2人达标,2人获奖,不利于提高工人的积极性;
当定额为200个时,有5人达标,5人获奖,不利于提高工人的积极性;
当定额为180个时,有9人达标,9人获奖,有利于提高大多数工人的积极性;
则定额为180个时,有利于提高大多数工人的积极性.
18.(1)由题意可知,甲种猕猴桃的测评分数在中有2个,故;乙种猕猴桃的测评分数在中有5个,故;
乙种猕猴桃的测评分数出现次数最多的是90,所以众数是90,即;
将甲种猕猴桃的测评分数从小到大排列处在中间位置的一个数是91,因此中位数是91,即;
(2)由甲、乙猕猴桃的测评分数大小波动情况,直观可得,
故答案为:;
(3)可以推断甲品种较好,理由为:①甲品种猕猴桃的测评分数的中位数、众数均比乙品种的高;②甲品种猕猴桃的测评分数方差比乙种小.
故答案为:甲;①甲品种猕猴桃的测评分数的中位数、众数均比乙品种的高,②甲品种猕猴桃的测评分数方差比乙种小.
19.(1)八年级的10名学生中有8名学生成绩低于90分,
,
根据众数的定义可知:,
把七年级10名学生的测试成绩排好顺序为:74,76,79,81,84,86,87,90,90,93,
根据中位数的定义可知,该组数据的中位数为,
故答案为:2,85,84;
(2)七年级10名学生的成绩中不低于85分的所占比例为,
八年级10名学生的成绩中不低于85分的所占比例为,
七年级测试成绩达到“优秀“的学生人数为:(人),
八年级测试成绩达到“优秀“的学生人数为:(人),
七、八年级测试成绩达到“优秀“的学生人数分别为100人和60人;
(3)七、八年级测试成绩的平均数相等,八年级测试成绩的方差小于七年级测试成绩的方差,
八年级的学生掌握防震减灾科普知识的总体水平较好.
20.(1)补全表格如下
成绩(分
人数 4 10 8 3
分析数据:补充完成下面的统计分析表:
平均数 中位数 方差
76 76 190.88
(2)“”这组数据75,76,78,80,81,82,85,87,88,88,
这组数据的众数是88分,
故答案为:88;
(3)估计全校九年级成绩达到90分及以上的学生人数为(人);
(4)从平均数看,八年级和九年级平均数相等,两个年级的平均成绩相等;
从中位数看,八年级的中位数大于九年级的中位数,所以八年级高分的人数多于九年级高分人数,八年级的成绩较好;
从方差看,八年级的方差小于九年级的方差,所以八年级的成绩比九年级的成绩稳定,八年级的成绩较好;
综上可知,八年级的成绩较好.
21.(1)由题意知,其众数,
女生锻炼时间的中位数为,
故答案为:6、70、70.5;
(2)估计该校九年级周末在家锻炼的时间在90分钟以上(不包含90分钟)同学的人数为(人);
(3)女生锻炼时间的平均数大于男生,女生锻炼时间的中位数大于男生.
22.(1)抽取20块八年级菜圃的评分(单位:分)
7,7,7,7,7,8,8,8,8,8,8,8,8,9,9,9,9,9,9,10.
第10,11个数均为8,故八年级中位数.
根据扇形统计图可知七、八年级抽取的菜圃,
七、八年级评为6分的共有(块),
评为7分的共有(块),
评为8分的共有(块),
评为9分的共有(块),
评为10分的共有(块),
则七年级评为6分的有(块),
评为7分的有(块),
评为8分的有(块),
评为9分的有(块),
评为10分的有(块),
七年级评为10分的最多,故众数.
故答案为:8;10;
(2)(块).
故可估计该校七年级“五星菜圃”的数量约为27块;
(3)七年级的菜圃耕种情况更好.理由如下:
因为七年级菜圃的中位数高于八年级的中位数,七年级菜圃的众数高于八年级的众数.
23.(1)(人).
故答案为:21;
(2)一班数据90出现12次,出现次数最多,所以众数为90,
二班100分的有11人,90分的有1人,80分的有9人,70分的有4人,按从小到大顺序排列,中位数为80;
平均数(分) 中位数(分) 众数(分)
一班 87.6 90 90
二班 87.6 80 100
①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班可以评为一等奖;
②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班可以评为一等奖;
③从级以上(包括级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班可以评为一等奖.
24.(1)分出现了次数最多,出现了5次,
七年级众数是45分,
,
八年级47分出现了5次,出现的次数最多,
则;
把八年级的20名学生的测评成绩从小到大排列,中位数是第10、11个数的平均数,
则(分).
故答案为:45,47,46;
(2)九年级二班的测评成绩好,
由表知,九年级二班测评成绩的平均数和中位数均大于九年级一班,
所以九年级二班测评成绩的平均水平和高分人数均比九年级一班高.
(3)估计此次测评活动成绩合格的学生人数约为(人).
25.(1)八(1)众数为85分,八(2)班的中位数为80分,
故答案为:85,80;
(2)八(1)的平均成绩是:(分);
(3)从平均数上看,均为85分,水平相当,
从中位数上看,八(1)班85分,八(2)班80分,(1)班好于(2)班,
所以八(1)班较好.
(4)八(2)的方差是:
,
,
八(1)班学生的成绩比较稳定.
第二十单元学习质量检测卷
时间:120分钟 满分:120分
班级__________姓名__________得分__________
一、选择题(共10小题,满分30分,每小题3分)
1.(3分)全国文明典范城市是全国文明城市的升级版,也是文明城市的标杆.2021年,长沙市抬高创建坐标,全力以赴推进“全国文明城市”向“全国文明典范城市”迭代升级.12月25日,长沙市文明办组织开展“长沙文明十二点”网络征集广纳建言活动,面向社会各界广泛征求意见和建议.芙蓉区某中学的小亮响应号召,对自己居住小区家庭使用垃圾袋的情况进行了调查,小亮随机调查了小区10户家庭一周垃圾袋的使用量,结果如下(单位:个),7,7,8,8,9,9,10,11,14,关于这组数据下列结论正确的是
A.平均数是10 B.众数是7 C.中位数是8 D.极差是6
2.(3分)为了增强学生的安全意识,某校组织学生开展了安全知识竟赛活动,经过一轮初赛后,共有21人进入决赛,本次活动将按照决赛分数评出一等奖2名,二等奖3名,三等奖5名.小丽进入了决寨,要判断自己能否获奖,她应当关注决赛分数的
A.平均数 B.众数 C.中位数 D.方差
3.(3分)描述一组数据的离散程度,我们还可以用“平均差”.在一组数、、、、中,各数据与它们的平均数的差的绝对值的平均数,即叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大,稳定性越小.现有甲、乙两组数据,如表所示,则下列说法错误的是
甲 12 13 11 15 13 14
乙 10 16 10 18 17 7
A.甲、乙两组数据的平均数相同
B.乙组数据的平均差为4
C.甲组数据的平均差是2
D.甲组数据更加稳定
4.(3分)在一次数学测验中,甲、乙、丙、丁四位同学的成绩(单位:分)分别是80,,80,70,若这四位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是
A.90分 B.85分 C.80分 D.75分
5.(3分)某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙、丁的成绩分析如表所示:
甲 乙 丙 丁
平均数 7.9 7.9 8.0 8.0
方差 3.29 0.49 1.8 0.4
根据以上图表信息,参赛选手应选
A.甲 B.乙 C.丙 D.丁
6.(3分)某校九年级(3)班全体学生2021年中考体育模拟考试的成绩统计如下表:
成绩(分 36 40 43 46 48 50 54
人数(人 2 5 6 7 8 7 5
根据上表中的信息判断,下列结论中错误的是
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是48分
C.该班学生这次考试成绩的中位数是47分
D.该班学生这次考试成绩的平均数是46分
7.(3分)根据某市统计局发布的该市近5年的年度增长率的有关数据,经济学家评论说,该市近5年的年度增长率相当平稳,从统计学的角度看,“增长率相当平稳”说明这组数据的 比较小.
A.中位数 B.平均数 C.众数 D.方差
8.(3分)对于一组数据,,4,2,下列结论不正确的是
A.平均数是1 B.方差是3.5 C.中位数是0.5 D.众数是
9.(3分)某组数据方差计算公式为:,由公式提供的信息,下列说法错误的是
A.样本的容量是3 B.样本的中位数是3
C.样本的众数是3 D.样本的平均数是3
10.(3分)某校6名学生在2020年中考中的体育成绩(满分50分)统计如图所示,则这组数据的众数、中位数分别是
A.50,48 B.48,49 C.50,49 D.48,48
二、填空题(共5小题,满分15分,每小题3分)
11.(3分)若一组数据2,3,4,5,的方差与另一组数据5,6,7,8,9的方差相等,则 .
12.(3分)某班有50人,一次数学测试后,老师对测试成绩进行了统计.由于小颖没有参加此次集体测试,因此计算其他49人的平均分为92分,方差.后来小颖进行了补测,成绩是92分,则该班50人的数学测试成绩的方差 (填“变小”、“不变”、“变大” .
13.(3分)已知一组数据,,,,的平均数是2,方差是5,那么另一组数据,,,,的平均数和方差的和为 .
14.(3分)为庆祝中国共产党建党100周年,某商校组织党史知识竞赛,根据小明、小刚5次预赛成绩绘制成统计图,下面三个推断:
①与小刚相比,小明5次成绩的极差大;
②与小刚相比,小明5次成绩的平均数大;
③与小刚相比,小明5次成绩的方差小;
④与小刚相比,小明的成绩比较稳定.
其中,所有合理推断的序号是 .
15.(3分)小明所在班级为希望工程捐款,他统计了全班同学的捐款情况,并绘制成如图所示的统计图,根据统计图,可计算出全班同学平均每人捐款 元.
三.解答题(共10小题,满分75分)
16.(7分)八年级举行锡越子比赛,每班推出5名学生参赛,按团体总分排列名次.下表是成绩最好的甲班和乙班各5名学生的比赛数据(单位:个).由于两班的总分、平均分都相等,数学老师提出:可否对所得数操作进一步处理,得出其他统计量作为评定的参考?同时,给出下列问题请你回答.
1号 2号 3号 4号 5号 总分
甲班 100 98 110 89 103 500
乙班 89 100 95 119 97 500
(1)计算两班比赛数据的中位数;
(2)计算两班比赛数据的方差;
(3)根据以上新统计量,作为团体,你认为应该把冠军奖状发给哪一个班级?请简单地说明理由!
17.(7分)某车间有工人10人,某月他们生产的零件个数统计如下表:
生产零件的个数(个) 600 480 220 180 120
工人人数(人) 1 1 3 4 1
(1)求这10名工人该月生产零件的平均个数;
(2)为了调动工人的积极性,决定实行目标管理,对完成目标的工人进行适当的奖励.如果想让一半左右的工人都能获得奖励,请你从平均数、中位数、众数的角度进行分析,该如何确定月生产目标?
18.(7分)农业农村经济在国民经济中占有重要地位,科技兴农、为促进乡村产业振兴提供有力支撑.为了解甲、乙两种新品猕猴桃的质量,进行了抽样调查.在相同条件下,随机抽取了甲、乙各25份样品,对大小、甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.
.测评分数(百分制)如下:
甲 77 79 80 80 85 86 86 87 88 89 89 90 91 91 91 91 91 92 93 95 95 96 97 98 98
乙 69 87 79 79 8679 87 89 90 89 90 90 90 91 90 92 92 94 92 95 96 96 97 98 98
.按如下分组整理、描述这两组样本数据:
测评分数 个数 品种
甲 0 9 14
乙 1 3 16
注:分数90分及以上为优秀,分为合格,80分以下为不合格.
.甲、乙两种猕猴桃测评分数的平均数、众数、中位数如表所示:
品种 平均数 众数 中位数
甲 89.4 91
乙 89.4 90
根据以上信息,回答下列问题:
(1)写出表中,,,的值;
(2)记甲种猕猴桃测评分数的方差为,乙种猕猴桃测评分数的方差为,则,的大小关系为 ;
(3)根据抽样调查情况,可以推断 种猕猴桃的质量较好,理由为 .(至少从两个不同的角度说明推断的合理性)
19.(7分)为进一步宣传防震减灾科普知识,增强学生应急避险和自救互救能力,某校组织七、八年级各200名学生进行“防震减灾知识测试”(满分100分).现分别在七、八年级中各随机抽取10名学生的测试成绩(单位:分)进行统计、整理如下:
七年级:86,90,79,84,74,93,76,81,90,87.
八年级:85,76,90,81,84,92,81,84,83,84
七八年级测试成绩频数统计表
七年级 3 4 3
八年级 1 7
七八年级测试成绩分析统计表
平均数 中位数 众数 方差
七年级 84 90 36.4
八年级 84 84 8.4
根据以上信息,解答下列问题:
(1) , , .
(2)规定分数不低于85分记为“优秀”,估计这两个年级测试成绩达到“优秀”的学生人数.
(3)你认为哪个年级的学生掌握防震减灾科普知识的总体水平较好?请说明理由.
20.(7分)随着十九届六中全会的召开,中学生对时事新闻的关注度高涨.某校组织全校学生开展“时事新闻大比拼”比赛,并随机抽取九年级的25名学生的成绩(满分为100分)进行分析.收集数据:25名学生的成绩(满分为100分)统计如下(单位:分):
90,74,88,65,98,75,81,44,85,70,55,80,95,88,72,87,60,56,76,66,78,72,82,63,100
整理数据:
成绩(分)
人数 10 8
分析数据:
平均数 中位数 方差
76 190.88
(1)将表格中的数据补充完整(3个);
(2)“”这组数据的众数是 分;
(3)若全校九年级有800名学生,请估计全校九年级有多少名学生成绩达到90分及以上?
(4)若八年级成绩的平均数为76分,中位数为80分,方差为102.5,你认为哪个年级的成绩较好?请你做出评价.(至少从两个方面说明)
21.(8分)2021年底,西安突发新冠肺炎疫情、在各方共同努力下,取得了抗击疫情的阶段性胜利.日前,新一波新冠肺炎疫情又在中国香港地区蔓延,同时深圳、呼和浩特等多地也出现散发病例.做好新冠肺炎疫情防控时刻不能放松,对中学生来说抗击疫情的最好办法是强身健体,提高免疫力.某校为了解九年级学生周末在家体育银炼的情况,在该校九年级随机抽收了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了如下数据(单位:分钟):
【收集数据】
男生:28,30,32,39,46,57,58,66,68,69,70,70,80,88,95,99,100,105;
女生:29,35,36,48,55,56,62,69,69,72,73,78,88,88,90,98,99,109.
【整理数据】
锻炼时间
男生 1 7 4
女生 1 5 8 4
【分析数据】两组数据的平均数、中位数、众数如表:
统计量 组别 平均数 中位数 众数
男生 66.7 68.5
女生 69.7 69、88
根据以上信息解答下列问题:
(1)填空: , , ;
(2)如果该校九年级的男生有270人、女生有360人,估计该校九年级周末在家锻炼的时间在90分钟以上(不包含90分钟)同学的人数;
(3)王老师看了表格数据后认为九年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持王老师观点的理由.
22.(8分)为了落实立德树人根本任务,积极响应“双减”政策要求,某校开设了丰富的劳动教育课程.某日,学生处对学校菜圃耕作情况进行了一次评分.从七、八年级各随机抽取20块菜圃,对这部分菜圃的评分进行整理和分析(采圃评分均为整数,满分为10分,9分(含9分)以上为“五星菜圃”).相关数据统计、整理如下:
抽取八年级菜圃的评分(单位:分):
7,7,7,7,7,8,8,8,8,8,8,9,9,9,9,9,9,9,9,10.
七、八年级抽取的菜圃评分统计
年级 七年级 八年级
平均数 8.25 8.25
中位数 9
众数 9
方差 2.5875 0.7875
根据以上信息,解答下列问题:(1)填空: , ;
(2)该校七年级共19个班,每班有4块菜圃,估计该校七年级“五星菜圃”的数量;
(3)根据以上数据分析,从一个方面评价两个年级的菜圃耕种情况谁更好.
23.(8分)某校策划了一次有关党的知识竞赛,每班参加比赛的人数相同,成绩分为,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将九年级一班和二班的成绩进行整理并绘制成如下统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中,一班成绩在级以上(包括级)的人数为 人.
(2)请你根据平均数、众数、中位数等统计知识,综合阐述哪个班整体水平较高,可以评为一等奖?
24.(8分)我校为了提高学生的文明意识,举办了“文明知识”测评活动.现从九年级一班和二班中各随机抽取20名学生的测评成绩(满分50分,45分及45分以上为优秀,40分及40分以上为合格)进行整理、描述和分析,给出了下面的部分信息.
九年级一班20名学生的测评成绩(单位:分)分别为:
44 50 40 40 50 45 45 45 49 45 44 42 49 42 49 49 45 42 38 42
九年级二班20名学生的测评成绩统计图如图所示.
两个班抽取的学生的测评成绩的平均数、众数、中位数如表:
班级 平均数 众数 中位数
一班 44.75 45
二班 44.9
请你根据上面提供的所有信息,解容下列问题:
(1)表中的 , , .
(2)根据以上数据,你认为在此次测评中,九年级一班的测评成绩好还是九年级二班的测评成绩好?请说明理由(说明一条理由即可);
(3)已知学校九年级共800名学生参加了此次测评活动,通过计算,请你估计此次测评活动成绩合格的学生人数.
25.(8分)某中学开展“唱歌”比赛活动,八(1),八(2)班各选出5名选手参加复赛,5名选手的复赛成绩(满分为100分),如图所示:
(1)根据图示填写下表:
班级 中位数分 众数分
八(1)班 85
八(2)班 100
(2)通过计算得知八(2)的平均成绩为85分,请计算八(1)的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)经计算八(1)班复赛成绩的方差为70,请计算八(2)班复赛成绩的方差,并说明哪个班学生的成绩比较稳定.
参考答案
一、选择题(共10小题,满分30分,每小题3分)
1.B; 2.C; 3.C; 4.C; 5.D; 6.D; 7.D; 8.B; 9.A; 10.D;
二、填空题(共5小题,满分15分,每小题3分)
11.1或6;
12.变小;
13.49;
14.③④;
15.41;
三、解答题(共10小题,满分75分)
16.(1)甲班的中位数为100,乙班的中位数为98;
(2)甲班平均分为:,
;
乙班平均分为:,
乙班的方差为:;
(3)应该把冠军奖状发给甲班.
因为两班的平均分相同,但甲班的优秀率比乙班高,比赛数据的中位数也比乙班大,甲班比赛数据的方差比乙班小,说明甲班的成绩比乙班稳定,综合分析,甲班成绩好,所以应该把冠军奖状发给甲班.
17.(1)根据题意得:
(个).
答:这10名工人该月生产零件的平均个数为258个;
(2)共有10名工人,
中位数为(个),众数为180个,
当定额为258个时,有2人达标,2人获奖,不利于提高工人的积极性;
当定额为200个时,有5人达标,5人获奖,不利于提高工人的积极性;
当定额为180个时,有9人达标,9人获奖,有利于提高大多数工人的积极性;
则定额为180个时,有利于提高大多数工人的积极性.
18.(1)由题意可知,甲种猕猴桃的测评分数在中有2个,故;乙种猕猴桃的测评分数在中有5个,故;
乙种猕猴桃的测评分数出现次数最多的是90,所以众数是90,即;
将甲种猕猴桃的测评分数从小到大排列处在中间位置的一个数是91,因此中位数是91,即;
(2)由甲、乙猕猴桃的测评分数大小波动情况,直观可得,
故答案为:;
(3)可以推断甲品种较好,理由为:①甲品种猕猴桃的测评分数的中位数、众数均比乙品种的高;②甲品种猕猴桃的测评分数方差比乙种小.
故答案为:甲;①甲品种猕猴桃的测评分数的中位数、众数均比乙品种的高,②甲品种猕猴桃的测评分数方差比乙种小.
19.(1)八年级的10名学生中有8名学生成绩低于90分,
,
根据众数的定义可知:,
把七年级10名学生的测试成绩排好顺序为:74,76,79,81,84,86,87,90,90,93,
根据中位数的定义可知,该组数据的中位数为,
故答案为:2,85,84;
(2)七年级10名学生的成绩中不低于85分的所占比例为,
八年级10名学生的成绩中不低于85分的所占比例为,
七年级测试成绩达到“优秀“的学生人数为:(人),
八年级测试成绩达到“优秀“的学生人数为:(人),
七、八年级测试成绩达到“优秀“的学生人数分别为100人和60人;
(3)七、八年级测试成绩的平均数相等,八年级测试成绩的方差小于七年级测试成绩的方差,
八年级的学生掌握防震减灾科普知识的总体水平较好.
20.(1)补全表格如下
成绩(分
人数 4 10 8 3
分析数据:补充完成下面的统计分析表:
平均数 中位数 方差
76 76 190.88
(2)“”这组数据75,76,78,80,81,82,85,87,88,88,
这组数据的众数是88分,
故答案为:88;
(3)估计全校九年级成绩达到90分及以上的学生人数为(人);
(4)从平均数看,八年级和九年级平均数相等,两个年级的平均成绩相等;
从中位数看,八年级的中位数大于九年级的中位数,所以八年级高分的人数多于九年级高分人数,八年级的成绩较好;
从方差看,八年级的方差小于九年级的方差,所以八年级的成绩比九年级的成绩稳定,八年级的成绩较好;
综上可知,八年级的成绩较好.
21.(1)由题意知,其众数,
女生锻炼时间的中位数为,
故答案为:6、70、70.5;
(2)估计该校九年级周末在家锻炼的时间在90分钟以上(不包含90分钟)同学的人数为(人);
(3)女生锻炼时间的平均数大于男生,女生锻炼时间的中位数大于男生.
22.(1)抽取20块八年级菜圃的评分(单位:分)
7,7,7,7,7,8,8,8,8,8,8,8,8,9,9,9,9,9,9,10.
第10,11个数均为8,故八年级中位数.
根据扇形统计图可知七、八年级抽取的菜圃,
七、八年级评为6分的共有(块),
评为7分的共有(块),
评为8分的共有(块),
评为9分的共有(块),
评为10分的共有(块),
则七年级评为6分的有(块),
评为7分的有(块),
评为8分的有(块),
评为9分的有(块),
评为10分的有(块),
七年级评为10分的最多,故众数.
故答案为:8;10;
(2)(块).
故可估计该校七年级“五星菜圃”的数量约为27块;
(3)七年级的菜圃耕种情况更好.理由如下:
因为七年级菜圃的中位数高于八年级的中位数,七年级菜圃的众数高于八年级的众数.
23.(1)(人).
故答案为:21;
(2)一班数据90出现12次,出现次数最多,所以众数为90,
二班100分的有11人,90分的有1人,80分的有9人,70分的有4人,按从小到大顺序排列,中位数为80;
平均数(分) 中位数(分) 众数(分)
一班 87.6 90 90
二班 87.6 80 100
①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班可以评为一等奖;
②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班可以评为一等奖;
③从级以上(包括级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班可以评为一等奖.
24.(1)分出现了次数最多,出现了5次,
七年级众数是45分,
,
八年级47分出现了5次,出现的次数最多,
则;
把八年级的20名学生的测评成绩从小到大排列,中位数是第10、11个数的平均数,
则(分).
故答案为:45,47,46;
(2)九年级二班的测评成绩好,
由表知,九年级二班测评成绩的平均数和中位数均大于九年级一班,
所以九年级二班测评成绩的平均水平和高分人数均比九年级一班高.
(3)估计此次测评活动成绩合格的学生人数约为(人).
25.(1)八(1)众数为85分,八(2)班的中位数为80分,
故答案为:85,80;
(2)八(1)的平均成绩是:(分);
(3)从平均数上看,均为85分,水平相当,
从中位数上看,八(1)班85分,八(2)班80分,(1)班好于(2)班,
所以八(1)班较好.
(4)八(2)的方差是:
,
,
八(1)班学生的成绩比较稳定.
