函数的单调性[上学期]
图片预览



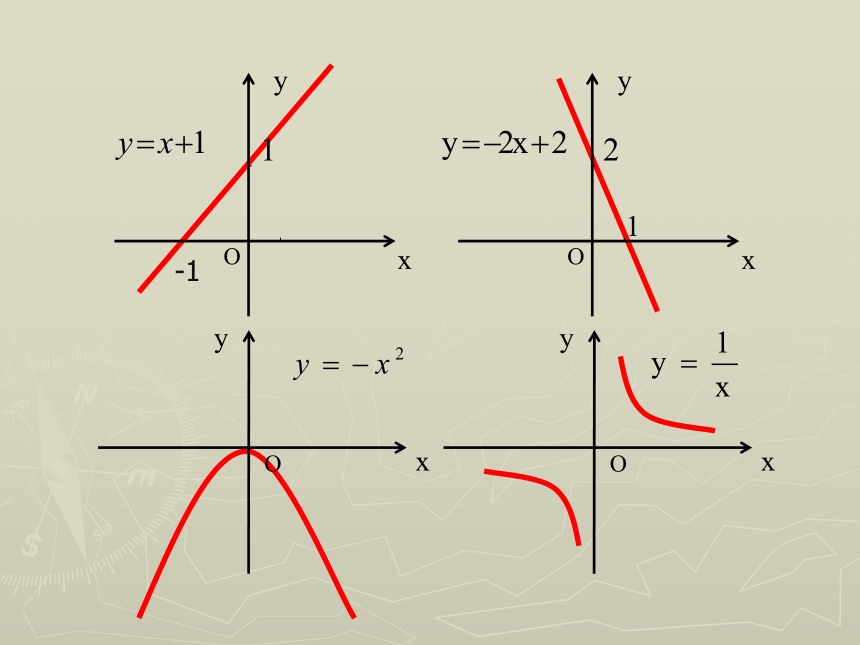
文档简介
课件29张PPT。函数的单调性 创设情境,引入新课
建立函数的目的是研究函数值与自变量的关系,自变量的变化对函数值变化的影响是经常受到关注的问题.例如水位的涨落随时间变化的规律,是防涝抗旱工作中必须解决的实际问题.下面我们开始研究函数在这方面的一个主要性质——函数的单调性.
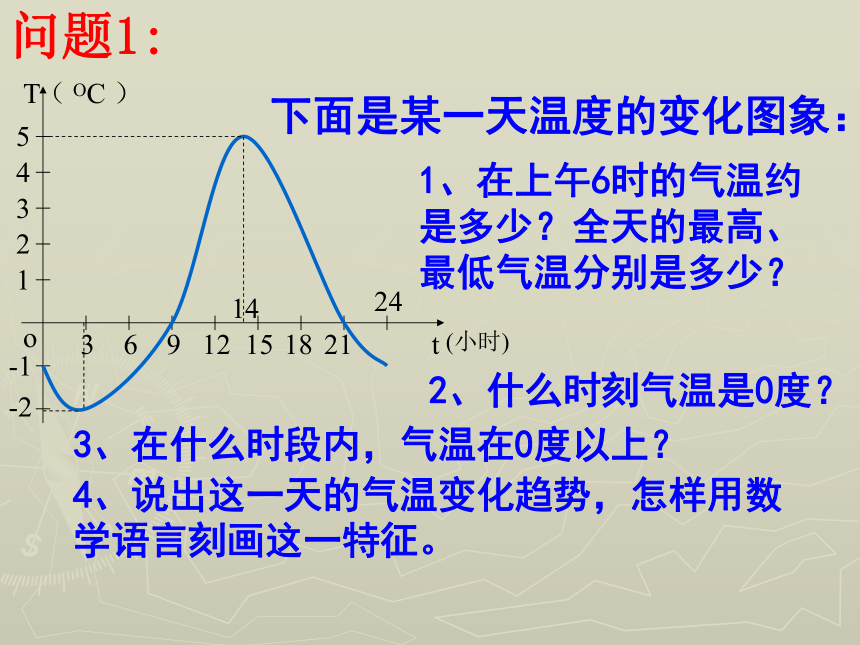
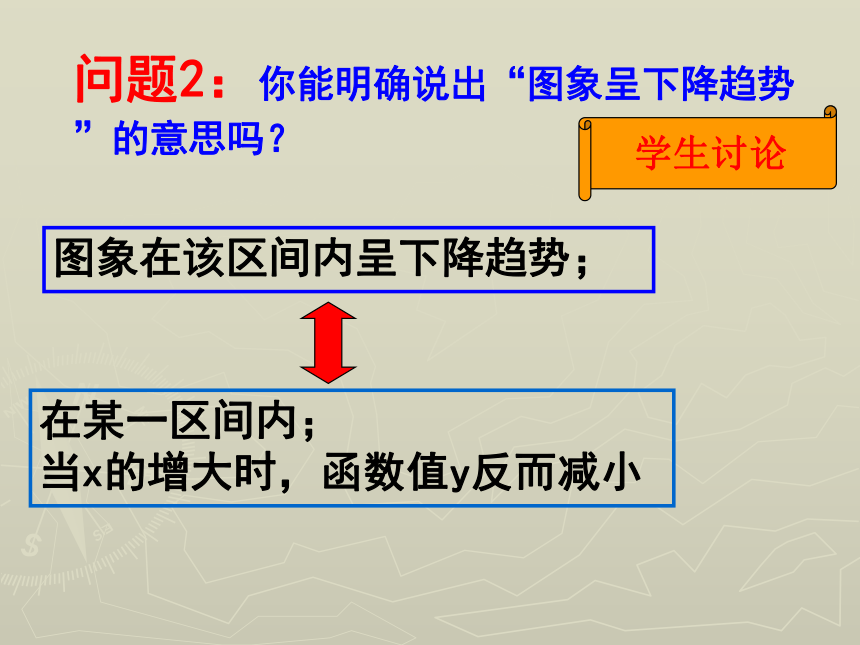
下面是某一天温度的变化图象:1、在上午6时的气温约是多少?全天的最高、最低气温分别是多少?2、什么时刻气温是0度?3、在什么时段内,气温在0度以上?4、说出这一天的气温变化趋势,怎样用数 学语言刻画这一特征。问题1:问题1、观察自己所作函数图象,并指出图象的变化的趋势学生活动自己作出下列函数的图象:-1问题2:你能明确说出“图象呈下降趋势”的意思吗?在某一区间内;
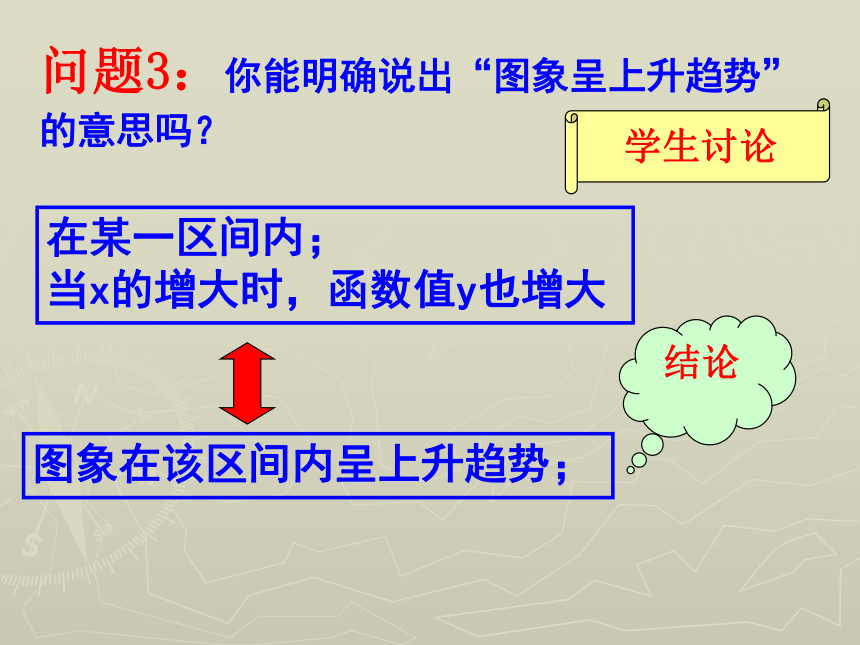
当x的增大时,函数值y反而减小学生讨论图象在该区间内呈下降趋势;问题3:你能明确说出“图象呈上升趋势”的意思吗?在某一区间内;
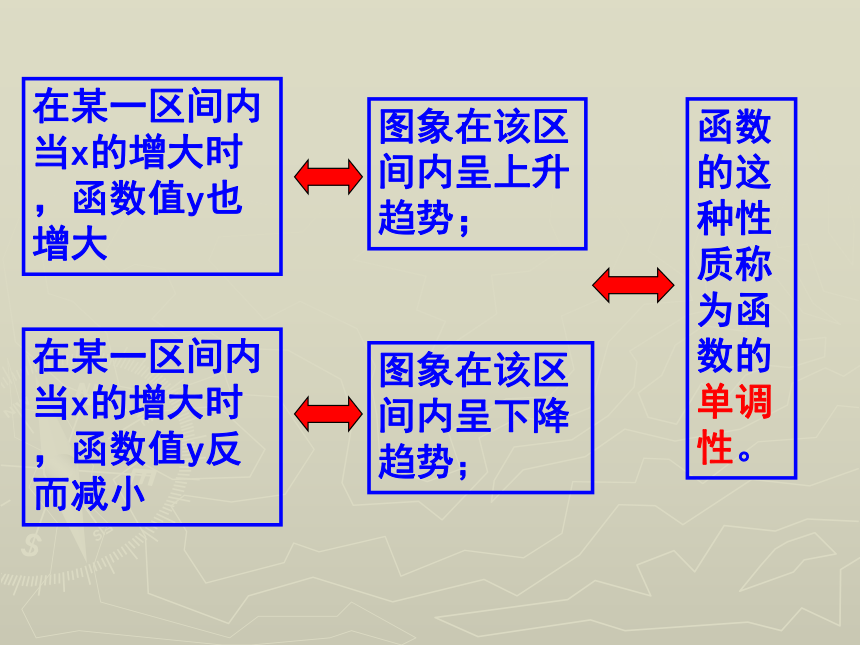
当x的增大时,函数值y也增大学生讨论结论图象在该区间内呈上升趋势;在某一区间内
当x的增大时,函数值y反而减小图象在该区间内呈下降趋势;在某一区间内
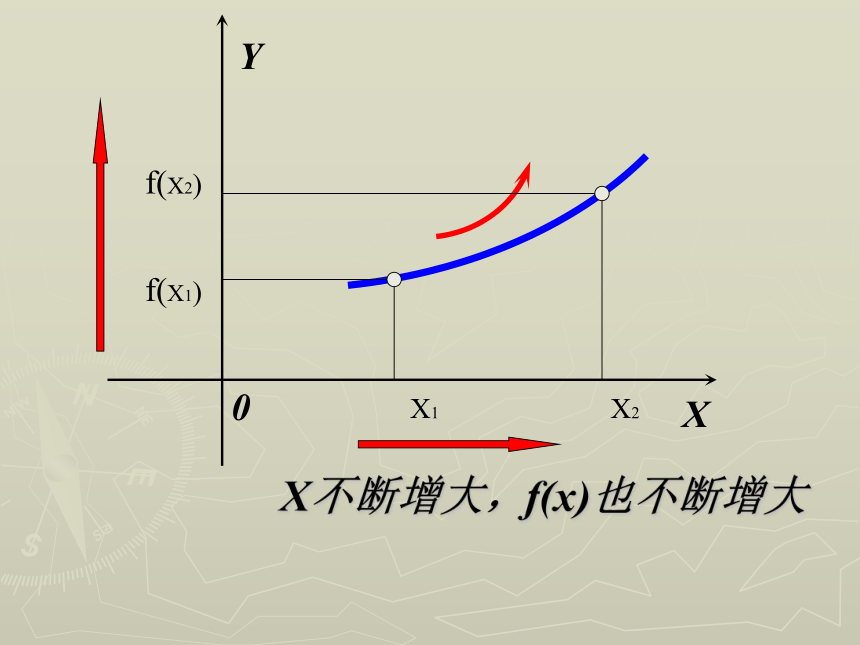
当x的增大时,函数值y也增大图象在该区间内呈上升趋势;函数的这 种性质称为函数的单调性。 X不断增大,f(x)也不断增大0 XYX1X2f(X1)f(X2)Y X0 X不断增大,f(x)不断减小X1X2f(X2)f(X1)函数f (x)在给定区间上为增函数。如何用x与 f(x)来描述上升的图象?如何用x与 f(x)来描述下降的图象?函数f (x)在给定区间上为减函数。如果对于属于定义域I内的某个区间上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)< f(x2),那么就说f(x).在这个区间上是增函数.如果对于属于定义域I内的某个区间上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)> f(x2),那么就说f(x) .在这个区间上是减函数.增函数与减函数定义建构数学说明1函数y=f(x)在区间D上是增函数或减函数,就称函数y=f(x)在区间D上具有单调性,
D称为函数的单调区间。说明2 说函数的单调性必须指出所对应的单调区间,单调区间可能是定义域的一部分(如:y=x2),也可能是全部定义域(如:y=x3);一个函数在定义域内可以划分出若干个单调区间,不同的单调区间上可以表现出不同的单调性.增函数和减函数的定义中两个变量x1,x2:
1. 必须在同一单调区间上;
2. 必须是任意的,不能用定值代替;
3. 必须设定它们的大小关系后,比
较y1,y2 的大小才有意义.
例:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-3),[-3,1)[1,3),[3,5].其中y=f(x)在[-5,-3), [1,3)上是减函数,在[-3,1), [3,5)上是增函数.数学应用 1. 如图,已知y=f(x) 的图象(包括端点),根据图象说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数. 作图是发现函数单调性的法之一
演练反馈单调递增区间:单调递减区间:例1:证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。注意:我们在证明函数的单调性时,不能“以图代证”, 而是严格按照定义证明.
回想一下,定义的本质是什么?本题怎样用定义来证明?证明:(条件)(论证结果)(结论)例1:证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。证明函数单调性的步骤:第一步:取值.即任取区间内的两个值,且x1第二步:作差变形.将f(x1)-f(x2)通过因式分解、配方、有理化等方法,向有利于判断差的符号的方向变形。第三步:定号.确定差的符号,适当的时候需要进行讨论。第四步:判断.根据定义作出结论。取值作差变形定号判断证明:设x1,x2∈(0,+∞),且x1<x2,则减函数例2:判断函数f(x)=1/x在区间(0,+∞)上是增函数还是减函数?并证明你的结论。 f(x)在定义域
上是减函数吗?解:函数 f(x)= x2+1 在(0,+∞)上是增函数.下面给予证明:设x1,x2∈(0,+∞),且x1<x2∴函数f(x)=x2+1在(0,+∞)上是增函数.例3:判断函数f(x)=x2+1在区间(0,+∞)上是增函数还是减函数?并给予证明。演练反馈2.求证:函数y= - 5x+3在R上为减函数.3.求证:函数f (x) = -x3 + 1在(- ∞, + ∞ )上是减函数. (能力提高题)证明: 设x1 ,x2∈R 且 x1 < x2∵ x1 = x13- x23 = (x1 -x2)(x12 + x1x2 + x22)∴f(x1) > f (x2) ∴f(x) = -x3 + 1在(-∞, + ∞)上是减函数. 小结:
(1)单调递增函数的定义:一般地,设函数f(x)的定义域为I,如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1(2)单调递减函数的定义:一般地,设函数f(x)的定义域为I,如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1f(x2),那么就说f(x)在这个区间上是减函数。
x1x2y1y2x2x1y1y2小结:作业(1):P37 练习: 1、2、5、6思考题:结合图象说出函数
的单调区间,以及在各个区间上是增函数还是
减函数;你能给出相应的证明吗?
谢谢
建立函数的目的是研究函数值与自变量的关系,自变量的变化对函数值变化的影响是经常受到关注的问题.例如水位的涨落随时间变化的规律,是防涝抗旱工作中必须解决的实际问题.下面我们开始研究函数在这方面的一个主要性质——函数的单调性.
下面是某一天温度的变化图象:1、在上午6时的气温约是多少?全天的最高、最低气温分别是多少?2、什么时刻气温是0度?3、在什么时段内,气温在0度以上?4、说出这一天的气温变化趋势,怎样用数 学语言刻画这一特征。问题1:问题1、观察自己所作函数图象,并指出图象的变化的趋势学生活动自己作出下列函数的图象:-1问题2:你能明确说出“图象呈下降趋势”的意思吗?在某一区间内;
当x的增大时,函数值y反而减小学生讨论图象在该区间内呈下降趋势;问题3:你能明确说出“图象呈上升趋势”的意思吗?在某一区间内;
当x的增大时,函数值y也增大学生讨论结论图象在该区间内呈上升趋势;在某一区间内
当x的增大时,函数值y反而减小图象在该区间内呈下降趋势;在某一区间内
当x的增大时,函数值y也增大图象在该区间内呈上升趋势;函数的这 种性质称为函数的单调性。 X不断增大,f(x)也不断增大0 XYX1X2f(X1)f(X2)Y X0 X不断增大,f(x)不断减小X1X2f(X2)f(X1)函数f (x)在给定区间上为增函数。如何用x与 f(x)来描述上升的图象?如何用x与 f(x)来描述下降的图象?函数f (x)在给定区间上为减函数。如果对于属于定义域I内的某个区间上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)< f(x2),那么就说f(x).在这个区间上是增函数.如果对于属于定义域I内的某个区间上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)> f(x2),那么就说f(x) .在这个区间上是减函数.增函数与减函数定义建构数学说明1函数y=f(x)在区间D上是增函数或减函数,就称函数y=f(x)在区间D上具有单调性,
D称为函数的单调区间。说明2 说函数的单调性必须指出所对应的单调区间,单调区间可能是定义域的一部分(如:y=x2),也可能是全部定义域(如:y=x3);一个函数在定义域内可以划分出若干个单调区间,不同的单调区间上可以表现出不同的单调性.增函数和减函数的定义中两个变量x1,x2:
1. 必须在同一单调区间上;
2. 必须是任意的,不能用定值代替;
3. 必须设定它们的大小关系后,比
较y1,y2 的大小才有意义.
例:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-3),[-3,1)[1,3),[3,5].其中y=f(x)在[-5,-3), [1,3)上是减函数,在[-3,1), [3,5)上是增函数.数学应用 1. 如图,已知y=f(x) 的图象(包括端点),根据图象说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数. 作图是发现函数单调性的法之一
演练反馈单调递增区间:单调递减区间:例1:证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。注意:我们在证明函数的单调性时,不能“以图代证”, 而是严格按照定义证明.
回想一下,定义的本质是什么?本题怎样用定义来证明?证明:(条件)(论证结果)(结论)例1:证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。证明函数单调性的步骤:第一步:取值.即任取区间内的两个值,且x1
(1)单调递增函数的定义:一般地,设函数f(x)的定义域为I,如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1
x1x2y1y2x2x1y1y2小结:作业(1):P37 练习: 1、2、5、6思考题:结合图象说出函数
的单调区间,以及在各个区间上是增函数还是
减函数;你能给出相应的证明吗?
谢谢
