2022-2023学年京改版九年级数学下册23.3轴对称变换同步精练(无答案)
文档属性
| 名称 | 2022-2023学年京改版九年级数学下册23.3轴对称变换同步精练(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 617.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 00:00:00 | ||
图片预览


文档简介
23.3轴对称变换同步精练
一、单选题
1、如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是( )
A.(﹣4,3)
B.(﹣4,2)
C.(4,2)或(﹣4,3)
D.(4,2)或(﹣4,2)或(﹣4,3)
2、如图,在平面直角坐标系中,△ABC位于第二象限,点B的坐标是(﹣5,2),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于于x轴对称的△A2B2C2,则点B的对应点B2的坐标是( )
A.(﹣3,2) B.(2,﹣3) C.(1,2) D.(﹣1,﹣2)
3、如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点处,则该蚂蚁要吃到饭粒需爬行的最短路径长是( )
A.13cm B.cm C.cm D.cm
4、下列说法中正确的有( ) 个
①坐标平面内的点与有序实数对是一一对应的;②点位于第三象限;③点到y轴的距离为m;④点和点关于x轴对称,则的值为5;⑤若,则点在第一、三象限角平分线上.
A.1 B.2 C.3 D.4
5、如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.0 B.5
C.6 D.7
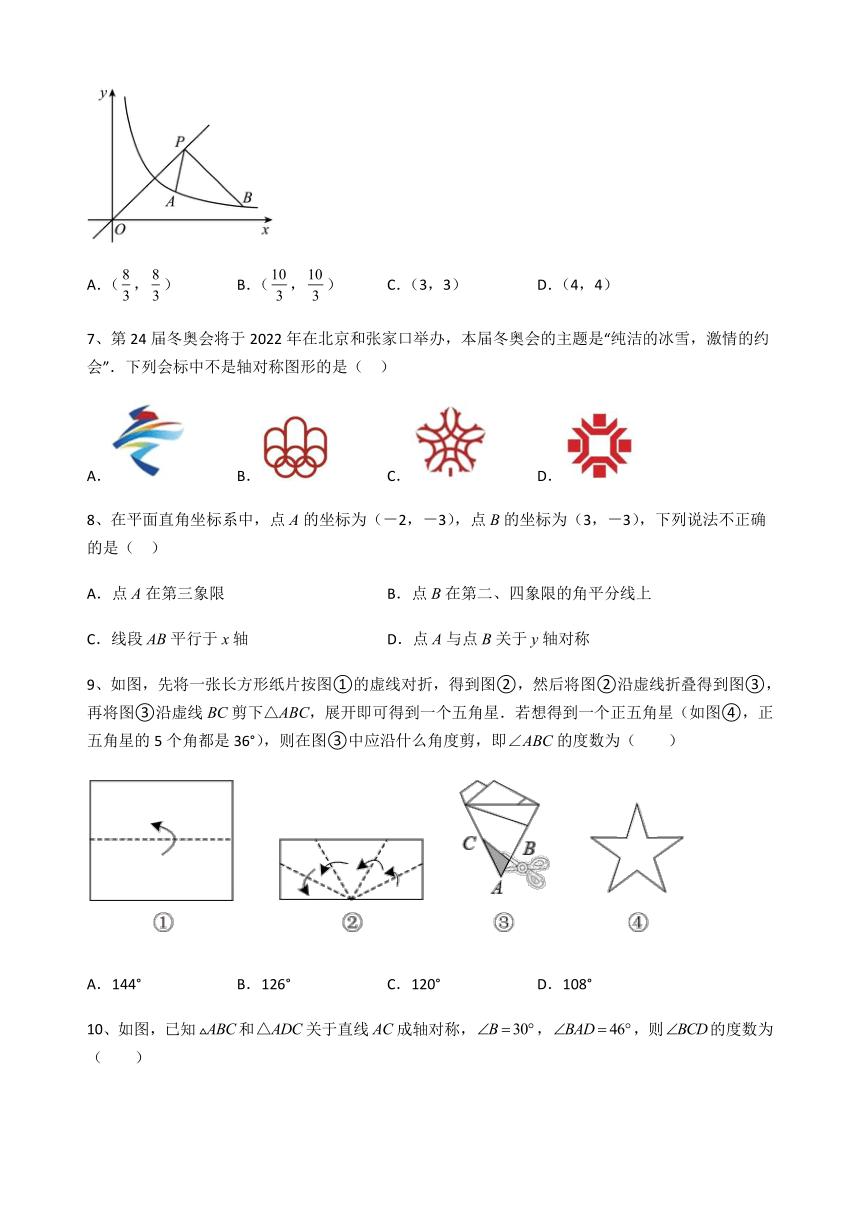
6、如图,点A(5a﹣1,2)、B(8,a)都在反比例函数y=(k≠0)的图象上,点P是直线y=x上的一个动点,当PA+PB最小时,点P坐标是( )
A.(,) B.(,) C.(3,3) D.(4,4)
7、第24届冬奥会将于2022年在北京和张家口举办,本届冬奥会的主题是“纯洁的冰雪,激情的约会”.下列会标中不是轴对称图形的是( )
A. B. C. D.
8、在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
9、如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪,即∠ABC的度数为( )
A.144° B.126° C.120° D.108°
10、如图,已知和关于直线成轴对称,,,则的度数为( )
A. B. C. D.
二、填空题
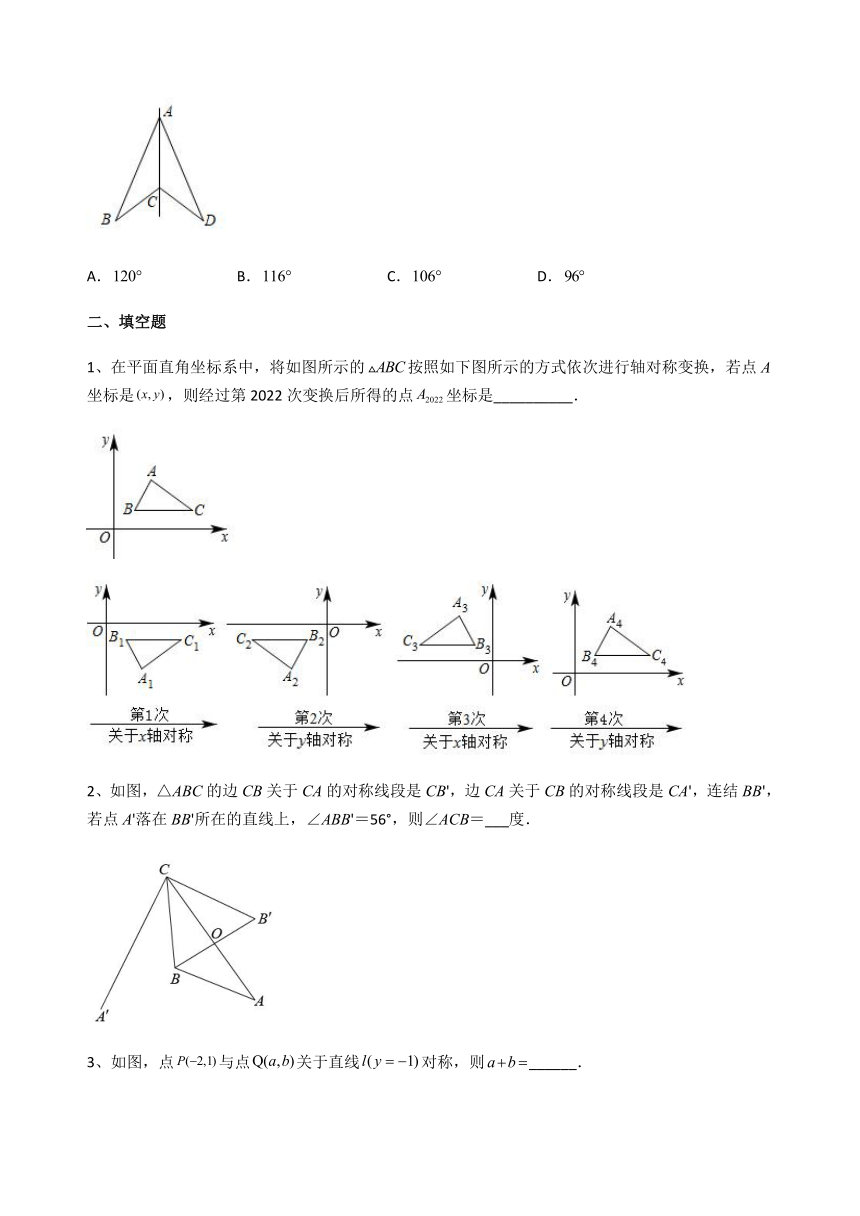
1、在平面直角坐标系中,将如图所示的按照如下图所示的方式依次进行轴对称变换,若点A坐标是,则经过第2022次变换后所得的点坐标是__________.
2、如图,△ABC的边CB关于CA的对称线段是CB',边CA关于CB的对称线段是CA',连结BB',若点A'落在BB'所在的直线上,∠ABB'=56°,则∠ACB=___度.
3、如图,点与点关于直线对称,则______.
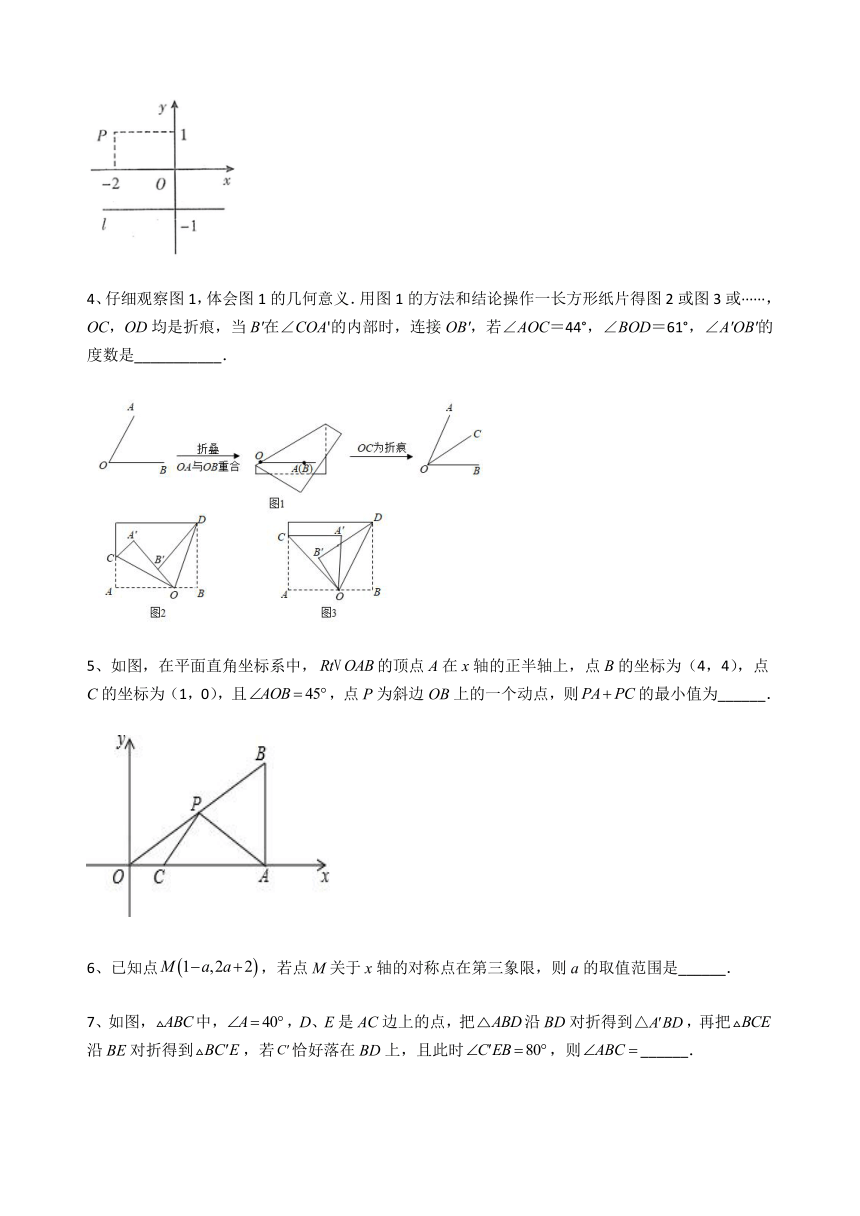
4、仔细观察图1,体会图1的几何意义.用图1的方法和结论操作一长方形纸片得图2或图3或······,OC,OD均是折痕,当B'在∠COA'的内部时,连接OB',若∠AOC=44°,∠BOD=61°,∠A'OB'的度数是___________.
5、如图,在平面直角坐标系中,的顶点A在x轴的正半轴上,点B的坐标为(4,4),点C的坐标为(1,0),且,点P为斜边OB上的一个动点,则的最小值为______.
6、已知点,若点M关于x轴的对称点在第三象限,则a的取值范围是______.
7、如图,中,,D、E是AC边上的点,把沿BD对折得到,再把沿BE对折得到,若恰好落在BD上,且此时,则______.
8、如图,在菱形ABCD中,,.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M的位置变化时,DF长的最大值为______.
三、解答题
1、如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1)B(4,2)C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是 ,此时C点关于这条直线的对称点C2的坐标为 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上确定一点P,使△APB的周长最小.(注:不写作法,不求坐标,只保留作图痕迹)
2、如图,在正方形网格中,点,,,,都在格点上.
(1)作关于直线对称的图形;
(2)若网格中最小正方形边长为1,求的面积;
(3)在直线上找一点,使得的值最大,并画出点的位置.
3、如图,抛物线与X轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,点D为抛物线对称轴上一动点.
(1)求直线BC的函数表达式;
(2)连接OD,CD,求周长的最小值;
(3)在抛物线上是否存在一点E.使以B、C、D、E为顶点的四边形是以BC为边的平行四边形?若存在,请直接写出E点的坐标;若不存在,请说明理由.
4、如图,在平面直角坐标系中,,,.
(1)已知与关于轴对称,画出;
(2)的面积是_________;
(3)在轴上找一点,使得的周长最小,点的坐标为_________.
5、综合与实践
在数学教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动——折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.
实践发现:
对折矩形纸片ABCD,使AD与BC重合,折痕为EF,把纸片展平:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,折痕为BM,把纸片展平,连接AN,如图①;
(1)折痕BM所在直线是否是线段AN的垂直平分线?请判断图中是什么特殊三角形?请写出解答过程.
(2)继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B,得到折痕BG,把纸片展平,如图②,求∠GBN的度数.
(3)拓展延伸:
如图③,折叠矩形纸片ABCD,使点A落在BC边上的点处,并且折痕交BC边于点T,交AD边于点S,把纸片展平,连接交ST于点O,连接AT;求证:四边形是菱形.
6、在平面直角坐标系中,的三个顶点的位置如图所示.
(1)请画出关于轴对称的;
(2)直接写出关于轴对称的的,,三点的坐标:__________,__________,__________;
(3)求的面积.
一、单选题
1、如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是( )
A.(﹣4,3)
B.(﹣4,2)
C.(4,2)或(﹣4,3)
D.(4,2)或(﹣4,2)或(﹣4,3)
2、如图,在平面直角坐标系中,△ABC位于第二象限,点B的坐标是(﹣5,2),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于于x轴对称的△A2B2C2,则点B的对应点B2的坐标是( )
A.(﹣3,2) B.(2,﹣3) C.(1,2) D.(﹣1,﹣2)
3、如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点处,则该蚂蚁要吃到饭粒需爬行的最短路径长是( )
A.13cm B.cm C.cm D.cm
4、下列说法中正确的有( ) 个
①坐标平面内的点与有序实数对是一一对应的;②点位于第三象限;③点到y轴的距离为m;④点和点关于x轴对称,则的值为5;⑤若,则点在第一、三象限角平分线上.
A.1 B.2 C.3 D.4
5、如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.0 B.5
C.6 D.7
6、如图,点A(5a﹣1,2)、B(8,a)都在反比例函数y=(k≠0)的图象上,点P是直线y=x上的一个动点,当PA+PB最小时,点P坐标是( )
A.(,) B.(,) C.(3,3) D.(4,4)
7、第24届冬奥会将于2022年在北京和张家口举办,本届冬奥会的主题是“纯洁的冰雪,激情的约会”.下列会标中不是轴对称图形的是( )
A. B. C. D.
8、在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
9、如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪,即∠ABC的度数为( )
A.144° B.126° C.120° D.108°
10、如图,已知和关于直线成轴对称,,,则的度数为( )
A. B. C. D.
二、填空题
1、在平面直角坐标系中,将如图所示的按照如下图所示的方式依次进行轴对称变换,若点A坐标是,则经过第2022次变换后所得的点坐标是__________.
2、如图,△ABC的边CB关于CA的对称线段是CB',边CA关于CB的对称线段是CA',连结BB',若点A'落在BB'所在的直线上,∠ABB'=56°,则∠ACB=___度.
3、如图,点与点关于直线对称,则______.
4、仔细观察图1,体会图1的几何意义.用图1的方法和结论操作一长方形纸片得图2或图3或······,OC,OD均是折痕,当B'在∠COA'的内部时,连接OB',若∠AOC=44°,∠BOD=61°,∠A'OB'的度数是___________.
5、如图,在平面直角坐标系中,的顶点A在x轴的正半轴上,点B的坐标为(4,4),点C的坐标为(1,0),且,点P为斜边OB上的一个动点,则的最小值为______.
6、已知点,若点M关于x轴的对称点在第三象限,则a的取值范围是______.
7、如图,中,,D、E是AC边上的点,把沿BD对折得到,再把沿BE对折得到,若恰好落在BD上,且此时,则______.
8、如图,在菱形ABCD中,,.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M的位置变化时,DF长的最大值为______.
三、解答题
1、如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1)B(4,2)C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是 ,此时C点关于这条直线的对称点C2的坐标为 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上确定一点P,使△APB的周长最小.(注:不写作法,不求坐标,只保留作图痕迹)
2、如图,在正方形网格中,点,,,,都在格点上.
(1)作关于直线对称的图形;
(2)若网格中最小正方形边长为1,求的面积;
(3)在直线上找一点,使得的值最大,并画出点的位置.
3、如图,抛物线与X轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,点D为抛物线对称轴上一动点.
(1)求直线BC的函数表达式;
(2)连接OD,CD,求周长的最小值;
(3)在抛物线上是否存在一点E.使以B、C、D、E为顶点的四边形是以BC为边的平行四边形?若存在,请直接写出E点的坐标;若不存在,请说明理由.
4、如图,在平面直角坐标系中,,,.
(1)已知与关于轴对称,画出;
(2)的面积是_________;
(3)在轴上找一点,使得的周长最小,点的坐标为_________.
5、综合与实践
在数学教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动——折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.
实践发现:
对折矩形纸片ABCD,使AD与BC重合,折痕为EF,把纸片展平:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,折痕为BM,把纸片展平,连接AN,如图①;
(1)折痕BM所在直线是否是线段AN的垂直平分线?请判断图中是什么特殊三角形?请写出解答过程.
(2)继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B,得到折痕BG,把纸片展平,如图②,求∠GBN的度数.
(3)拓展延伸:
如图③,折叠矩形纸片ABCD,使点A落在BC边上的点处,并且折痕交BC边于点T,交AD边于点S,把纸片展平,连接交ST于点O,连接AT;求证:四边形是菱形.
6、在平面直角坐标系中,的三个顶点的位置如图所示.
(1)请画出关于轴对称的;
(2)直接写出关于轴对称的的,,三点的坐标:__________,__________,__________;
(3)求的面积.
