2022—2023学年人教版数学九年级下册第二十七章 相似 单元自测题 (含解析)
文档属性
| 名称 | 2022—2023学年人教版数学九年级下册第二十七章 相似 单元自测题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 461.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 21:41:20 | ||
图片预览

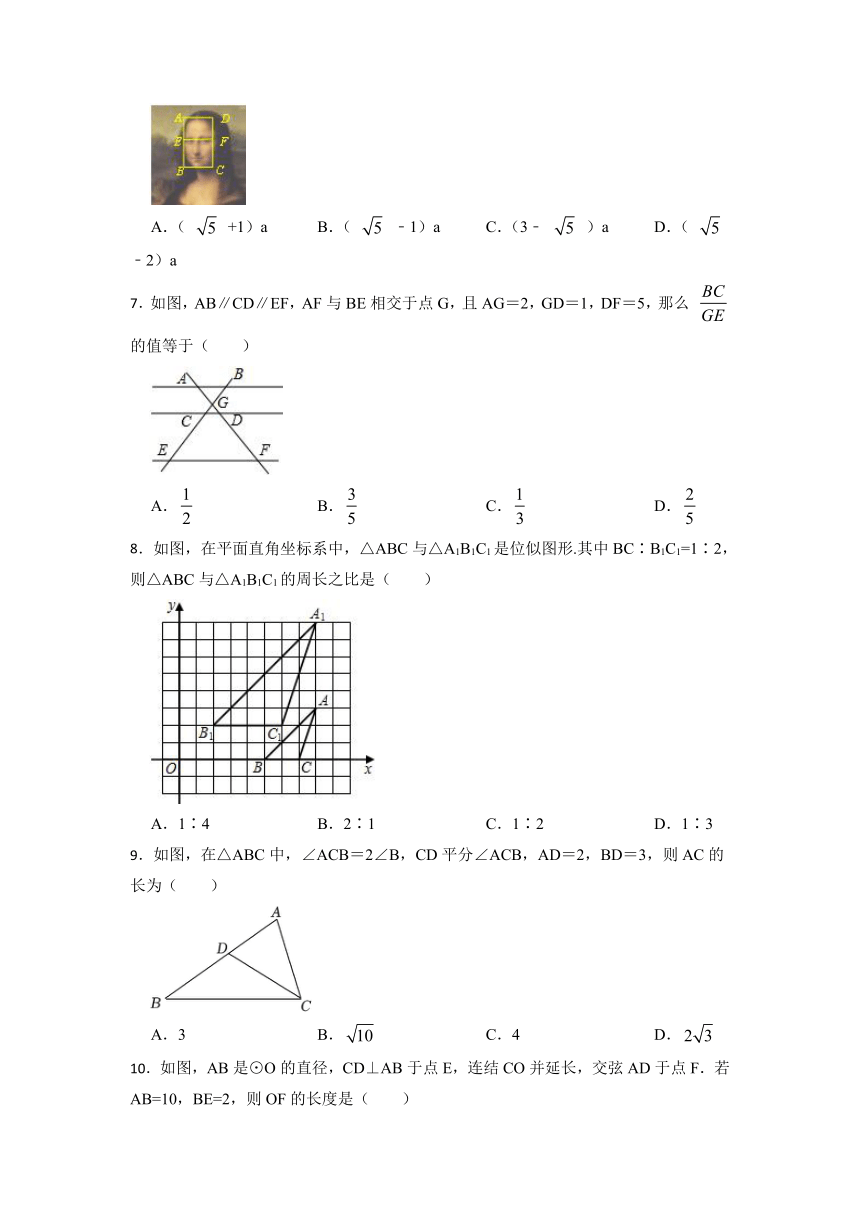

文档简介
人教版初中数学九年级下册 第二十七章 相似 单元自测题
一、单选题
1.如图,在△ABC中,D,E分别是AB,AC上的点,,若AD=6,BD=3,AE=8,则EC的长是( )
A.4 B.2 C.5 D.
2.若2a=3b,则 ( )
A. B. C. D.
3.若 且相似比为1:4,则 与 的面积比为( )
A.1:4 B.4:1 C.1:16 D.16:1
4.若,则的值为( )
A. B. C. D.
5.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
A. B.
C. D.
6.如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2a,则BE长为( )
A.( +1)a B.( ﹣1)a C.(3﹣ )a D.( ﹣2)a
7.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于( )
A. B. C. D.
8.如图,在平面直角坐标系中,△ABC与△A1B1C1是位似图形.其中BC∶B1C1=1∶2,则△ABC与△A1B1C1的周长之比是( )
A.1∶4 B.2∶1 C.1∶2 D.1∶3
9.如图,在△ABC中,∠ACB=2∠B,CD平分∠ACB,AD=2,BD=3,则AC的长为( )
A.3 B. C.4 D.
10.如图,AB是⊙O的直径,CD⊥AB于点E,连结CO并延长,交弦AD于点F.若AB=10,BE=2,则OF的长度是( )
A.
B.3
C.
D.
二、填空题
11.已知△ABC∽△DEF,相似比为3,则它们的周长之比是 .
12.若 = ,则 的值为 .
13.下列命题:①函数中,函数y随x的增大而减小,②有一个角相等的两个等腰三角形相似,③两个等边三角形相似,④平分弦的直径垂直于弦,⑤相等的圆周角所对的弧相等,⑥关于x的函数的图象是抛物线.其中正确的结论有 (填序号).
14.如图,AB是 O的直径,弦CD⊥AB于点E,F是弧BC上任意一点,线段AF与弦CD交于点G,连结FD和AD.
(1)若 ,则AD=
(2)在(1)的条件下,若CD= ,则 O的直径为 .
三、作图题
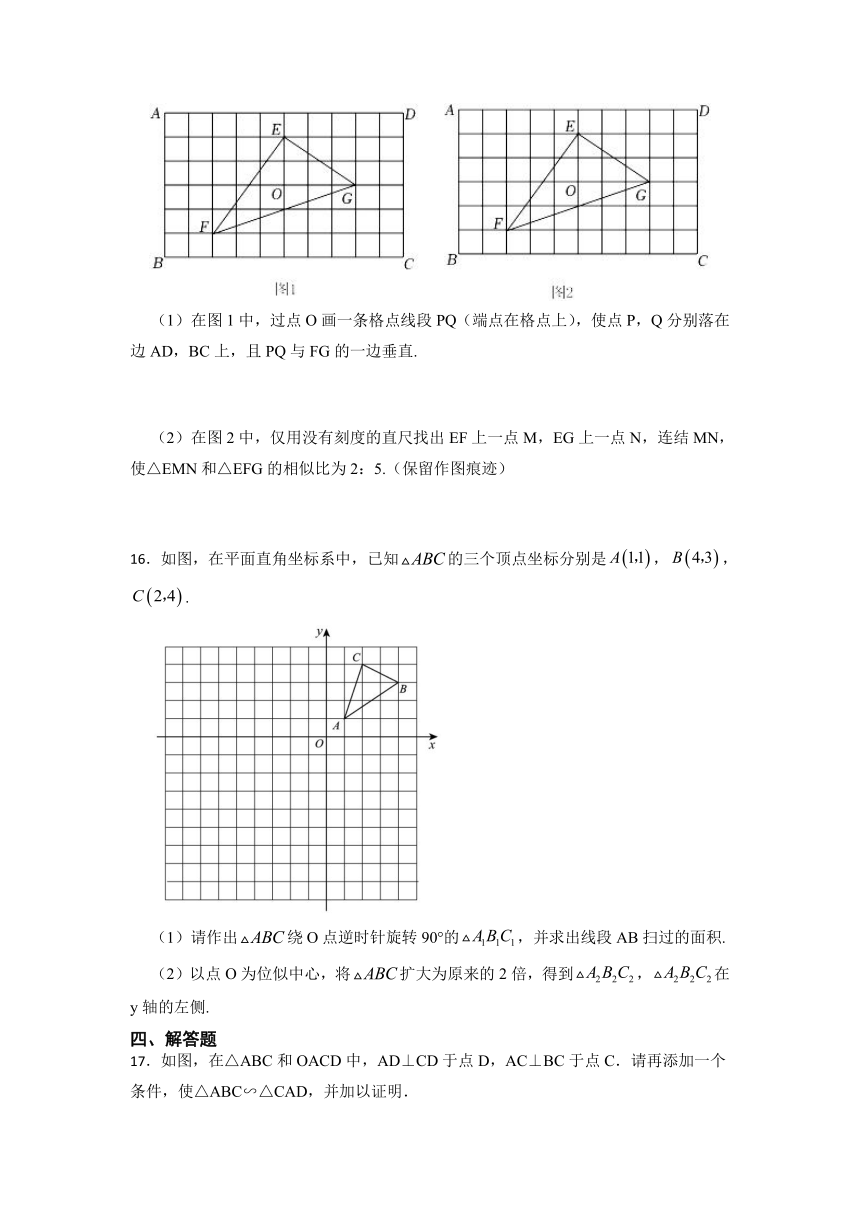
15.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.
(1) 在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.
(2) 在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)
16.如图,在平面直角坐标系中,已知的三个顶点坐标分别是,,.
(1)请作出绕O点逆时针旋转90°的,并求出线段AB扫过的面积.
(2)以点O为位似中心,将扩大为原来的2倍,得到,在y轴的左侧.
四、解答题
17.如图,在△ABC和OACD中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使△ABC∽△CAD,并加以证明.
18.人的肚脐是人的身高的黄金分割点,一般来讲,当肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段.一个身高1.70m的人,他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)?
19.如图,已知中,,求BD的长.
20.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
21.如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
五、综合题
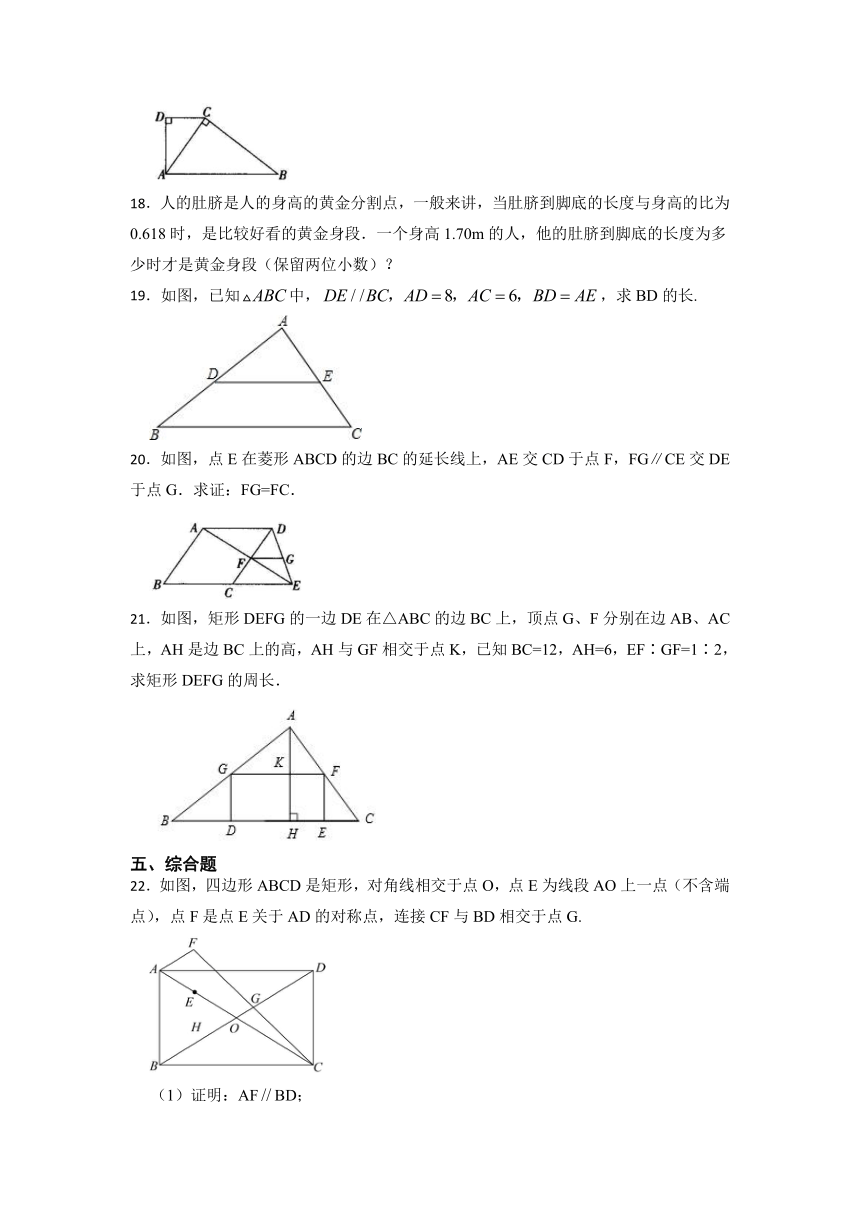
22.如图,四边形ABCD是矩形,对角线相交于点O,点E为线段AO上一点(不含端点),点F是点E关于AD的对称点,连接CF与BD相交于点G.
(1)证明:AFBD;
(2)若,.求BD的长.
23.如图,在Rt△ABC 中,∠C=90°,BC=5cm,AC=12cm。点M在边AB上,以2cm/s的速度由点B出发沿BA向点A匀速运动:同时点N在边AC上,以1cm/s的速度由点A出发沿AC向点C匀速运动。点M到达点A时,点M,N同时停止运动,连接MN,设点N运动的时间为ts:
(1)求AB的长;
(2)当t为何值时,△AMN的面积为△ABC的面积?
(3)是否存在t值,使得以A,M,N为顶点的三角形与△ABC相似?若存在,请求出t的值;若不存在,请说明理由。
答案解析部分
1.【答案】A
【解析】【解答】解:,
,
解得,
故答案为:A
【分析】由平行线分线段成比例可得,据此即可求解.
2.【答案】A
【解析】【解答】解:∵2a=3b,
∴ .
故答案为:A.
【分析】利用比例的性质:若a:b=c:d,则bc=ad,据此可求解.
3.【答案】C
【解析】【解答】解:∵△ABC∽△DEF,且相似比为1:4,
∴△ABC与△DEF的面积比为1:16,
故答案为:C.
【分析】相似三角形的面积比等于相似比的平方,据此解答即可.
4.【答案】D
【解析】【解答】解:∵,
∴,
∴.
故答案为:D.
【分析】由已知条件可得x= y,然后代入 中化简即可.
5.【答案】C
【解析】【解答】解:∵由图可知,AB=AC=6,∠B=75°,
∴∠C=75°,∠A=30°,
A选项中三角形各角的度数分别为75°,52.5°,52.5°,
B选项中三角形各角的度数都是60°,
C选项中三角形各角的度数分别为75°,30°,75°,
D选项中三角形各角的度数分别为40°,70°,70°,
∴只有C选项中三角形各角的度数与题干中三角形各角的度数相等,
故答案为:C.
【分析】根据“两组对应边的比相等且这两边的夹角相等的两个三角形相似”并结合各选项可判断求解.
6.【答案】B
【解析】【解答】解:∵点E是AB的黄金分割点,BE>AE,
∴BE= AB= 2a=( ﹣1)a.
故答案为:B.
【分析】根据黄金分割的定义:即把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比,其比值是(-1):2,根据定义列式求解即可.
7.【答案】A
【解析】【解答】解:∵AG=2,GD=1,DF=5,
∴AD=AG+GD=3,GF=GD+DF=6,
∵AB∥CD∥EF,
∴ = = = ,
故答案为:A.
【分析】根据平行线分线段成比例定理即可判断得出答案.
8.【答案】C
【解析】【解答】解:∵△ABC与△A1B1C1是位似图形,BC∶B1C1=1∶2,
∴△ABC与△A1B1C1的周长之比=BC∶B1C1=1∶2.
故答案为:C.
【分析】根据位似图形的周长比等于相似比进行解答.
9.【答案】B
【解析】【解答】解:∵CD平分∠ACB,
∴∠ACB=2∠ACD
∵∠ACB=2∠B,
∴∠ACD=∠B
又∠A=∠A
∴△ACD∽△ABC
∴=
∵AD=2,BD=3
∴AB= AD+BD=2+3=5
∴AC=.
故答案为:B.
【分析】根据角平分线的概念可得∠ACB=2∠ACD,结合已知条件可得∠ACD=∠B,又∠A=∠A,利用有两组角相等的两个三角形相似证明△ACD∽△ABC,接下来根据相似三角形的性质进行计算.
10.【答案】C
【解析】【解答】解:如图,过点O作OH⊥AB交AD于点H,
∵AB=10,
∴AO=BO=CO=5,
∵BE=2,
∴OE=3,
∵CD⊥AB,
∴CE=DE,
在Rt△OEC中,CE= =4,
∴CD=2CE=8,
∵OH∥CD,
∴,即,
∴解得OF=.
故答案为:C.
【分析】过点O作OH⊥AB交AD于点H,利用AB=10及BE=2求得OE=3;再根据垂径定理得CE=DE,在Rt△OEC中,利用勾股定理求得CE=4,进而求得CD;再由平行线分线段成比例得 ,代入数据即可求得OF的长度.
11.【答案】3
【解析】【解答】解:∵△ABC∽△DEF,相似比为3,
∴它们的周长之比为3,
故答案为:3.
【分析】利用相似三角形的周长比等于相似比,可得答案.
12.【答案】
【解析】【解答】解:由 = ,
设a=5k,b=2k,
把a=5k,b=2k代入得 ,
故答案为: .
【分析】由 = ,可设a=5k,则b=2k,将它们代入,就是即可求出其值.
13.【答案】③
【解析】【解答】解:①函数中,在每个象限内,函数y随x的增大而减小,故原说法错误;
②当一个等腰三角形的顶角与另一个三角形的底角相等时,两个三角形不相似,故原说法错误;
③因等边三角形的三个角都等于60°,所以两个等边三角形相似,故原说法正确;
④平分弦(不是直径)的直径垂直于弦,故原说法错误;
⑤同圆或等圆中,相等的圆周角所对的弧相等,故原说法错误;
⑥关于x的函数(a≠0)的图象是抛物线,故原说法错误.
故答案为:③.
【分析】根据反比例函数的性质可判断①;根据相似三角形的判定定理可判断②③;根据垂径定理可判断④;根据弧、圆周角的关系可判断⑤;根据二次函数的图象可判断⑥.
14.【答案】(1)
(2)
【解析】【解答】解:(1)连接FB、DB,
∵AB为直径,
∴∠AFB=90°,∠ADB=90°,
∴∠AFB=∠AEG=90°,
∵∠EAG=∠FAB,
∴△AEG∽△AFB,
∴,
∴AE×AB=AF×AF=15,
∵∠AEB=∠ADB,∠DAE=∠BAD,
∴△AEB∽△ADB,
∴,
∴AD2=AE×AB=15,
∴AD= ,
故答案为: ;
(2)∵CD⊥AB ,
∴ED=EC=,
∴AE=,
∵AD2=AE×AB,
∴AB==,
故答案为:.
【分析】(1)连接FB、DB,由直径所对的圆周角是直角可得∠AFB=90°,∠ADB=90°,则可证明△AEG∽△AFB,△AEG∽△AFB,利用相似三角形的性质推得AD2=AE×AB=15,即可求出AD的长;
(2)先根据勾股定理求出AE的长,然后代入AD2=AE×AB即可求出AB.
15.【答案】(1)解:如图1中,线段PQ即为所求;
(2)解:如图2中,线段MN即为所求.
【解析】【分析】(1)用三角尺一边与FG重合,另一个三角尺直角边与O重合,再AD和BC上找到P、Q两个格点,用直线连接PQ即可;
(2)取格点J、K,并连接OJ交EF于点M,连接OK交EG于点N,再连接MN即可.
16.【答案】(1)解:∵的三个顶点坐标分别是,,
∴绕O点逆时针旋转90°,得,,
如图所示:
即为所求
∵,
∴,
线段AB扫过的面积;
(2)解:∵的三个顶点坐标分别是,,
∴,,
如图所示,
即为所求.
【解析】【分析】(1)根据旋转的性质找出点A、B、C绕点O逆时针旋转90°的对应点A1、B1、C1的位置,顺次连接可得△A1B1C1,易得线段AB扫过的面积为:圆心角为90°,半径分别为OB、OA的扇形的面积之差,据此计算;
(2)分别给点A、B、C的横纵坐标乘以-2,可得点A2、B2、C2的坐标,找出对应的位置,然后顺次连接即可.
17.【答案】添加条件:AB∥CD.
证明:∵AD⊥CD,AC⊥BC,
∴∠ADC=∠ACB=90°,
∵AB∥CD,
∴∠CAB=∠DCA
∴△ABC∽△CAD.
【解析】【分析】本题的已知条件中已经有 AD⊥CD,AC⊥BC,即∠ADC=∠ACB=90° ,要想使 △ABC∽△CAD, 只需再找一组对应角相等,或夹角两边对应成比例,添加 AB∥CD,利用两直线平行内错角相等,即为∠CAB=∠DCA .
18.【答案】解:设他的肚脐到脚底的长度为xm时才是黄金身段,
根据题意得x:1.70=0.618,
即x=1.70×0.618≈1.1(m).
答:他的肚脐到脚底的长度为1.1m时才是黄金身段
【解析】【分析】他的肚脐到脚底的长度为xm时才是黄金身段,根据肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段,则x:1.70=0.618,然后解方程即可.
19.【答案】解:∵DE∥BC,
∴AD:AB=AE:AC,
又∵BD=AE,AD=8,AC=6,
∴AB=8+BD,
∴8:(8+BD)=BD:6即BD2+8BD-48=0.
解得:BD=4或BD=-12(不合题意,舍去)
【解析】【分析】根据平行线分线段成比例可得AD:AB=AE:AC, 据此即可求解.
20.【答案】证明:四边形ABCD是菱形,
∴AB=AD,DC∥AB,AD∥BC,
∵FC∥BC,
∵FG∥AD,
∴ ,
∴
∴FG=FC
【解析】【分析】由菱形的性质可知对边平行,四条边相等,然后利用平行线分线段成比例,列出比例式,等量代换即可.
21.【答案】解:如图,设EF=x,则GF=2x.∵GF∥BC,AH⊥BC,∴AK⊥GF.
∵GF∥BC,∴△AGF∽△ABC,
∴ = .
∵AH=6,BC=12,
∴ = .解得x=3.
∴矩形DEFG的周长为18.
【解析】【分析】由已知EF∶GF=1∶2,可设EF=x,GF=2x,由题意易证△AGF∽△ABC,再利用相似三角形的对应边成比例建立关于x的方程,解方程求出x的值,然后求出GF的长,由此可得到矩形DEFG的周长。
22.【答案】(1)解:∵点F是点E关于AD的对称点,
∴∠EAD=∠FAD,AE=AF,
∵四边形ABCD是矩形,
∴OA=OD
∴∠OAD=∠ODA,
∴∠FAD=∠ODA,
∴AFBD;
(2)解:∵O是矩形ABCD的对角线的交点,
∴O是AC的中点,
∴ AO=CO=AC
∵AFBD,
∴∠COG=∠CAF,∠CGO=∠ F
∴△COG∽△CAF
∴=
∴CG=CF
∴G为CF的中点,
∴OG是△CAF的中位线,
∴AF=2OG=2×1=2,
∴AE=2,
∵OE=2,
∴OA=AE+OE=4,
∴AC=2OA=8,
∴BD=AC=8.
【解析】【分析】(1)利用轴对称的性质可证得∠EAD=∠FAD,AE=AF,利用矩形的性质可得到OA=OD;再利用等腰三角形的性质去证明∠FAD=∠ODA;然后利用平行线的判定定理可证得结论.
(2)利用矩形的性质可知AO=CO=AC,利用平行线的性质可证得∠COG=∠CAF,∠CGO=∠ F,由此可推出△COG∽△CAF,利用相似三角形的对应边成比例可得到G为CF的中点;再利用三角形的中位线的性质可求出AF及AE的长;然后求出OA的长,即可求出BD的长.
23.【答案】(1)解:在Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,
∴
(2)解:如图:作MH⊥AC于H,则MH∥BC,
由题意得,BM=2t,AN=t,则AM=13-2t,
∵MH∥BC
△AMH∽△ABC
∴,即
解得 , ,
由题意得 , ,
解得 ,
(3)解:∵∠A=∠A
∴当 时,
∴
解得,
当 日寸, , ,
∴,
解得, ,
答 : 当 或 时,以 A, M, N 为顶点的三角 形与 相似
【解析】【分析】(1)直接利用勾股定理即可得出AB的长;
(2)作MH⊥AC于H,得出MH∥BC,得出△AMH∽△ABC,从而得出 ,再根据三角形的面积公式列出方程,解方程求出t的值,即可得出答案;
(3)分两种情况讨论:当 时,, 当 时,, 分别列出方程,解方程求出t的值,即可得出答案.
一、单选题
1.如图,在△ABC中,D,E分别是AB,AC上的点,,若AD=6,BD=3,AE=8,则EC的长是( )
A.4 B.2 C.5 D.
2.若2a=3b,则 ( )
A. B. C. D.
3.若 且相似比为1:4,则 与 的面积比为( )
A.1:4 B.4:1 C.1:16 D.16:1
4.若,则的值为( )
A. B. C. D.
5.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
A. B.
C. D.
6.如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2a,则BE长为( )
A.( +1)a B.( ﹣1)a C.(3﹣ )a D.( ﹣2)a
7.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于( )
A. B. C. D.
8.如图,在平面直角坐标系中,△ABC与△A1B1C1是位似图形.其中BC∶B1C1=1∶2,则△ABC与△A1B1C1的周长之比是( )
A.1∶4 B.2∶1 C.1∶2 D.1∶3
9.如图,在△ABC中,∠ACB=2∠B,CD平分∠ACB,AD=2,BD=3,则AC的长为( )
A.3 B. C.4 D.
10.如图,AB是⊙O的直径,CD⊥AB于点E,连结CO并延长,交弦AD于点F.若AB=10,BE=2,则OF的长度是( )
A.
B.3
C.
D.
二、填空题
11.已知△ABC∽△DEF,相似比为3,则它们的周长之比是 .
12.若 = ,则 的值为 .
13.下列命题:①函数中,函数y随x的增大而减小,②有一个角相等的两个等腰三角形相似,③两个等边三角形相似,④平分弦的直径垂直于弦,⑤相等的圆周角所对的弧相等,⑥关于x的函数的图象是抛物线.其中正确的结论有 (填序号).
14.如图,AB是 O的直径,弦CD⊥AB于点E,F是弧BC上任意一点,线段AF与弦CD交于点G,连结FD和AD.
(1)若 ,则AD=
(2)在(1)的条件下,若CD= ,则 O的直径为 .
三、作图题
15.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.
(1) 在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.
(2) 在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)
16.如图,在平面直角坐标系中,已知的三个顶点坐标分别是,,.
(1)请作出绕O点逆时针旋转90°的,并求出线段AB扫过的面积.
(2)以点O为位似中心,将扩大为原来的2倍,得到,在y轴的左侧.
四、解答题
17.如图,在△ABC和OACD中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使△ABC∽△CAD,并加以证明.
18.人的肚脐是人的身高的黄金分割点,一般来讲,当肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段.一个身高1.70m的人,他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)?
19.如图,已知中,,求BD的长.
20.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
21.如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
五、综合题
22.如图,四边形ABCD是矩形,对角线相交于点O,点E为线段AO上一点(不含端点),点F是点E关于AD的对称点,连接CF与BD相交于点G.
(1)证明:AFBD;
(2)若,.求BD的长.
23.如图,在Rt△ABC 中,∠C=90°,BC=5cm,AC=12cm。点M在边AB上,以2cm/s的速度由点B出发沿BA向点A匀速运动:同时点N在边AC上,以1cm/s的速度由点A出发沿AC向点C匀速运动。点M到达点A时,点M,N同时停止运动,连接MN,设点N运动的时间为ts:
(1)求AB的长;
(2)当t为何值时,△AMN的面积为△ABC的面积?
(3)是否存在t值,使得以A,M,N为顶点的三角形与△ABC相似?若存在,请求出t的值;若不存在,请说明理由。
答案解析部分
1.【答案】A
【解析】【解答】解:,
,
解得,
故答案为:A
【分析】由平行线分线段成比例可得,据此即可求解.
2.【答案】A
【解析】【解答】解:∵2a=3b,
∴ .
故答案为:A.
【分析】利用比例的性质:若a:b=c:d,则bc=ad,据此可求解.
3.【答案】C
【解析】【解答】解:∵△ABC∽△DEF,且相似比为1:4,
∴△ABC与△DEF的面积比为1:16,
故答案为:C.
【分析】相似三角形的面积比等于相似比的平方,据此解答即可.
4.【答案】D
【解析】【解答】解:∵,
∴,
∴.
故答案为:D.
【分析】由已知条件可得x= y,然后代入 中化简即可.
5.【答案】C
【解析】【解答】解:∵由图可知,AB=AC=6,∠B=75°,
∴∠C=75°,∠A=30°,
A选项中三角形各角的度数分别为75°,52.5°,52.5°,
B选项中三角形各角的度数都是60°,
C选项中三角形各角的度数分别为75°,30°,75°,
D选项中三角形各角的度数分别为40°,70°,70°,
∴只有C选项中三角形各角的度数与题干中三角形各角的度数相等,
故答案为:C.
【分析】根据“两组对应边的比相等且这两边的夹角相等的两个三角形相似”并结合各选项可判断求解.
6.【答案】B
【解析】【解答】解:∵点E是AB的黄金分割点,BE>AE,
∴BE= AB= 2a=( ﹣1)a.
故答案为:B.
【分析】根据黄金分割的定义:即把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比,其比值是(-1):2,根据定义列式求解即可.
7.【答案】A
【解析】【解答】解:∵AG=2,GD=1,DF=5,
∴AD=AG+GD=3,GF=GD+DF=6,
∵AB∥CD∥EF,
∴ = = = ,
故答案为:A.
【分析】根据平行线分线段成比例定理即可判断得出答案.
8.【答案】C
【解析】【解答】解:∵△ABC与△A1B1C1是位似图形,BC∶B1C1=1∶2,
∴△ABC与△A1B1C1的周长之比=BC∶B1C1=1∶2.
故答案为:C.
【分析】根据位似图形的周长比等于相似比进行解答.
9.【答案】B
【解析】【解答】解:∵CD平分∠ACB,
∴∠ACB=2∠ACD
∵∠ACB=2∠B,
∴∠ACD=∠B
又∠A=∠A
∴△ACD∽△ABC
∴=
∵AD=2,BD=3
∴AB= AD+BD=2+3=5
∴AC=.
故答案为:B.
【分析】根据角平分线的概念可得∠ACB=2∠ACD,结合已知条件可得∠ACD=∠B,又∠A=∠A,利用有两组角相等的两个三角形相似证明△ACD∽△ABC,接下来根据相似三角形的性质进行计算.
10.【答案】C
【解析】【解答】解:如图,过点O作OH⊥AB交AD于点H,
∵AB=10,
∴AO=BO=CO=5,
∵BE=2,
∴OE=3,
∵CD⊥AB,
∴CE=DE,
在Rt△OEC中,CE= =4,
∴CD=2CE=8,
∵OH∥CD,
∴,即,
∴解得OF=.
故答案为:C.
【分析】过点O作OH⊥AB交AD于点H,利用AB=10及BE=2求得OE=3;再根据垂径定理得CE=DE,在Rt△OEC中,利用勾股定理求得CE=4,进而求得CD;再由平行线分线段成比例得 ,代入数据即可求得OF的长度.
11.【答案】3
【解析】【解答】解:∵△ABC∽△DEF,相似比为3,
∴它们的周长之比为3,
故答案为:3.
【分析】利用相似三角形的周长比等于相似比,可得答案.
12.【答案】
【解析】【解答】解:由 = ,
设a=5k,b=2k,
把a=5k,b=2k代入得 ,
故答案为: .
【分析】由 = ,可设a=5k,则b=2k,将它们代入,就是即可求出其值.
13.【答案】③
【解析】【解答】解:①函数中,在每个象限内,函数y随x的增大而减小,故原说法错误;
②当一个等腰三角形的顶角与另一个三角形的底角相等时,两个三角形不相似,故原说法错误;
③因等边三角形的三个角都等于60°,所以两个等边三角形相似,故原说法正确;
④平分弦(不是直径)的直径垂直于弦,故原说法错误;
⑤同圆或等圆中,相等的圆周角所对的弧相等,故原说法错误;
⑥关于x的函数(a≠0)的图象是抛物线,故原说法错误.
故答案为:③.
【分析】根据反比例函数的性质可判断①;根据相似三角形的判定定理可判断②③;根据垂径定理可判断④;根据弧、圆周角的关系可判断⑤;根据二次函数的图象可判断⑥.
14.【答案】(1)
(2)
【解析】【解答】解:(1)连接FB、DB,
∵AB为直径,
∴∠AFB=90°,∠ADB=90°,
∴∠AFB=∠AEG=90°,
∵∠EAG=∠FAB,
∴△AEG∽△AFB,
∴,
∴AE×AB=AF×AF=15,
∵∠AEB=∠ADB,∠DAE=∠BAD,
∴△AEB∽△ADB,
∴,
∴AD2=AE×AB=15,
∴AD= ,
故答案为: ;
(2)∵CD⊥AB ,
∴ED=EC=,
∴AE=,
∵AD2=AE×AB,
∴AB==,
故答案为:.
【分析】(1)连接FB、DB,由直径所对的圆周角是直角可得∠AFB=90°,∠ADB=90°,则可证明△AEG∽△AFB,△AEG∽△AFB,利用相似三角形的性质推得AD2=AE×AB=15,即可求出AD的长;
(2)先根据勾股定理求出AE的长,然后代入AD2=AE×AB即可求出AB.
15.【答案】(1)解:如图1中,线段PQ即为所求;
(2)解:如图2中,线段MN即为所求.
【解析】【分析】(1)用三角尺一边与FG重合,另一个三角尺直角边与O重合,再AD和BC上找到P、Q两个格点,用直线连接PQ即可;
(2)取格点J、K,并连接OJ交EF于点M,连接OK交EG于点N,再连接MN即可.
16.【答案】(1)解:∵的三个顶点坐标分别是,,
∴绕O点逆时针旋转90°,得,,
如图所示:
即为所求
∵,
∴,
线段AB扫过的面积;
(2)解:∵的三个顶点坐标分别是,,
∴,,
如图所示,
即为所求.
【解析】【分析】(1)根据旋转的性质找出点A、B、C绕点O逆时针旋转90°的对应点A1、B1、C1的位置,顺次连接可得△A1B1C1,易得线段AB扫过的面积为:圆心角为90°,半径分别为OB、OA的扇形的面积之差,据此计算;
(2)分别给点A、B、C的横纵坐标乘以-2,可得点A2、B2、C2的坐标,找出对应的位置,然后顺次连接即可.
17.【答案】添加条件:AB∥CD.
证明:∵AD⊥CD,AC⊥BC,
∴∠ADC=∠ACB=90°,
∵AB∥CD,
∴∠CAB=∠DCA
∴△ABC∽△CAD.
【解析】【分析】本题的已知条件中已经有 AD⊥CD,AC⊥BC,即∠ADC=∠ACB=90° ,要想使 △ABC∽△CAD, 只需再找一组对应角相等,或夹角两边对应成比例,添加 AB∥CD,利用两直线平行内错角相等,即为∠CAB=∠DCA .
18.【答案】解:设他的肚脐到脚底的长度为xm时才是黄金身段,
根据题意得x:1.70=0.618,
即x=1.70×0.618≈1.1(m).
答:他的肚脐到脚底的长度为1.1m时才是黄金身段
【解析】【分析】他的肚脐到脚底的长度为xm时才是黄金身段,根据肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段,则x:1.70=0.618,然后解方程即可.
19.【答案】解:∵DE∥BC,
∴AD:AB=AE:AC,
又∵BD=AE,AD=8,AC=6,
∴AB=8+BD,
∴8:(8+BD)=BD:6即BD2+8BD-48=0.
解得:BD=4或BD=-12(不合题意,舍去)
【解析】【分析】根据平行线分线段成比例可得AD:AB=AE:AC, 据此即可求解.
20.【答案】证明:四边形ABCD是菱形,
∴AB=AD,DC∥AB,AD∥BC,
∵FC∥BC,
∵FG∥AD,
∴ ,
∴
∴FG=FC
【解析】【分析】由菱形的性质可知对边平行,四条边相等,然后利用平行线分线段成比例,列出比例式,等量代换即可.
21.【答案】解:如图,设EF=x,则GF=2x.∵GF∥BC,AH⊥BC,∴AK⊥GF.
∵GF∥BC,∴△AGF∽△ABC,
∴ = .
∵AH=6,BC=12,
∴ = .解得x=3.
∴矩形DEFG的周长为18.
【解析】【分析】由已知EF∶GF=1∶2,可设EF=x,GF=2x,由题意易证△AGF∽△ABC,再利用相似三角形的对应边成比例建立关于x的方程,解方程求出x的值,然后求出GF的长,由此可得到矩形DEFG的周长。
22.【答案】(1)解:∵点F是点E关于AD的对称点,
∴∠EAD=∠FAD,AE=AF,
∵四边形ABCD是矩形,
∴OA=OD
∴∠OAD=∠ODA,
∴∠FAD=∠ODA,
∴AFBD;
(2)解:∵O是矩形ABCD的对角线的交点,
∴O是AC的中点,
∴ AO=CO=AC
∵AFBD,
∴∠COG=∠CAF,∠CGO=∠ F
∴△COG∽△CAF
∴=
∴CG=CF
∴G为CF的中点,
∴OG是△CAF的中位线,
∴AF=2OG=2×1=2,
∴AE=2,
∵OE=2,
∴OA=AE+OE=4,
∴AC=2OA=8,
∴BD=AC=8.
【解析】【分析】(1)利用轴对称的性质可证得∠EAD=∠FAD,AE=AF,利用矩形的性质可得到OA=OD;再利用等腰三角形的性质去证明∠FAD=∠ODA;然后利用平行线的判定定理可证得结论.
(2)利用矩形的性质可知AO=CO=AC,利用平行线的性质可证得∠COG=∠CAF,∠CGO=∠ F,由此可推出△COG∽△CAF,利用相似三角形的对应边成比例可得到G为CF的中点;再利用三角形的中位线的性质可求出AF及AE的长;然后求出OA的长,即可求出BD的长.
23.【答案】(1)解:在Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,
∴
(2)解:如图:作MH⊥AC于H,则MH∥BC,
由题意得,BM=2t,AN=t,则AM=13-2t,
∵MH∥BC
△AMH∽△ABC
∴,即
解得 , ,
由题意得 , ,
解得 ,
(3)解:∵∠A=∠A
∴当 时,
∴
解得,
当 日寸, , ,
∴,
解得, ,
答 : 当 或 时,以 A, M, N 为顶点的三角 形与 相似
【解析】【分析】(1)直接利用勾股定理即可得出AB的长;
(2)作MH⊥AC于H,得出MH∥BC,得出△AMH∽△ABC,从而得出 ,再根据三角形的面积公式列出方程,解方程求出t的值,即可得出答案;
(3)分两种情况讨论:当 时,, 当 时,, 分别列出方程,解方程求出t的值,即可得出答案.
