算法初步[上学期]

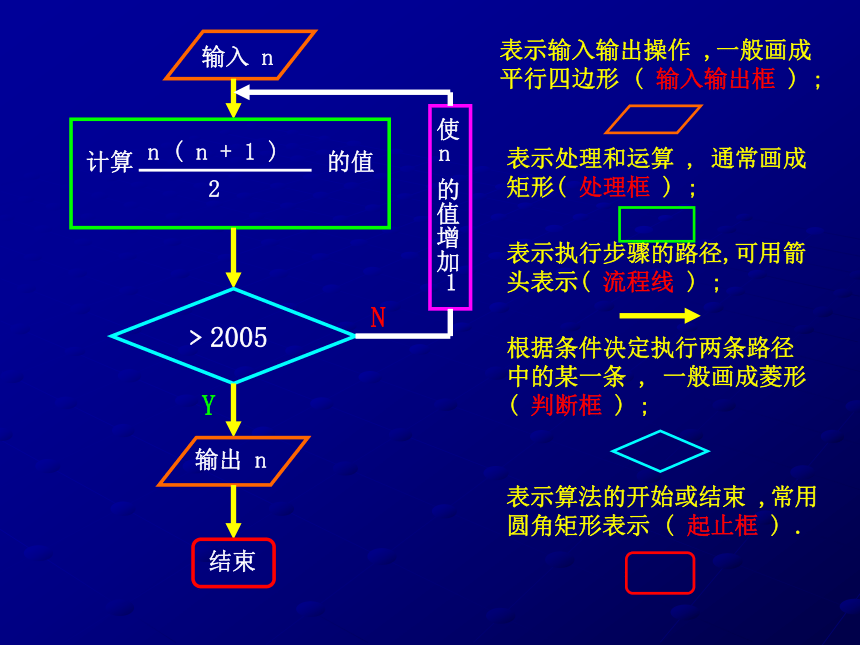
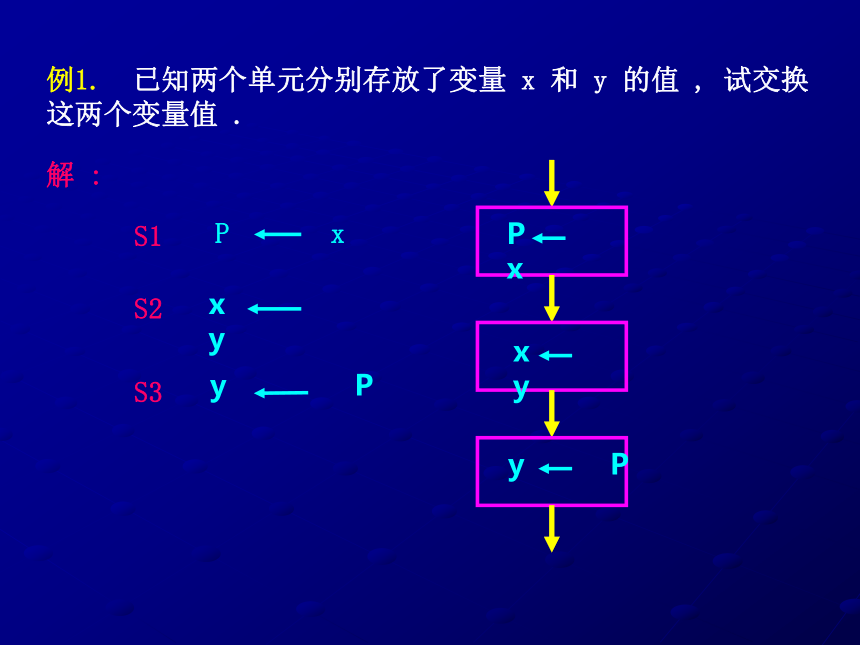
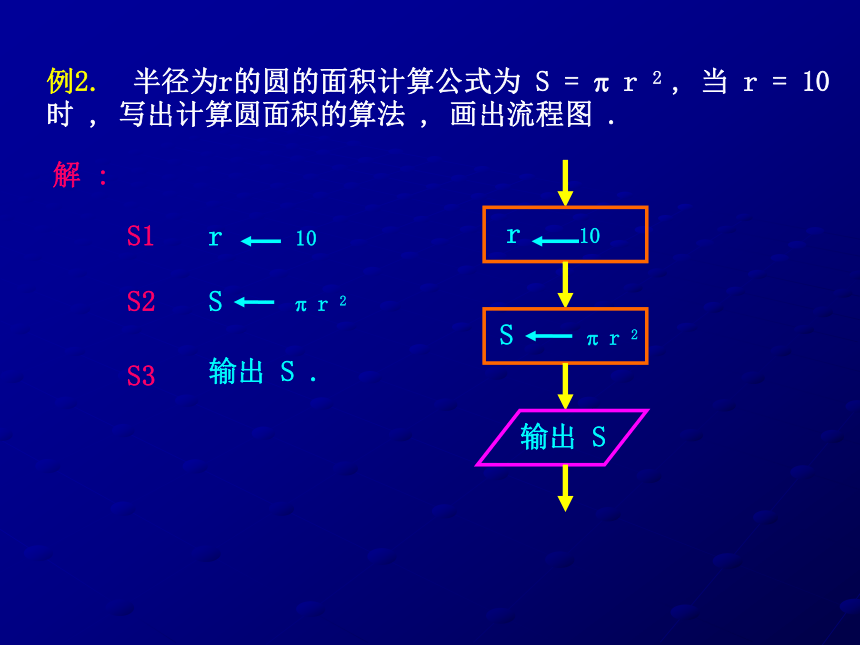
课件59张PPT。第五章 算 法 初 步5.1 算 法 的 含 义引例: 电视娱乐节目中,有一种有趣的 “ 猜数 ” 游戏 :竟猜者在规定的时间内猜出某种商品的价格 ( 或重量等 ), 就可获得该件商品 .例1. 给出求 1 + 2 + 3 + 4 + 5 的一个算法 .算法1:第1步计算 1 + 2 , 得 3 ;第2步将第 1 步中的运算结果 3 与 3 相加 , 得到 6 ;第3步将第 2 步中的运算结果 6 与 4 相加 , 得到 10 ;第4步将第 3 步中的运算结果 10 与 5 相加 , 得到 15 ;算法2:第1步取 n = 5 ;第2步第3步输出运算结果.算法3:第1步让 S = 0 , I = 1 ;第2步将 S + I 的值赋给 S , I 的值增加 1 ;第3步如果 I 比 5 大 , 则输出 S , 否则转到第二步 .解 :第1步方程 ( 1 ) 不动 , 将方程 ( 2 ) 中的 x 的系数除以方程 ( 1 ) 中的 x 的系数 , 得到系数 m = 2 ;第2步方程 ( 2 ) 减去 m 乘以方程 ( 1 ) , 消去方程 ( 2 ) 中的 x 项 , 得到第3步将上面的方程组自下而上回代求解 , 得到 y = - 1 , x = 4 .所以方程组的解为解 :练习1.写出解方程 2 x + 3 = 0 的一个算法过程 .第1步移项得 2 x = - 3 ;第2步两边同除以 2 得 x = - 3/2 .解 :练习2.写出求 1 ? 3 ? 5 ? 7 的一个算法 .第1步计算 1 ? 3 , 得 3 ;第2步将第 1 步中的运算结果 3 与 5 相乘 , 得到 15 ;第3步将第 2 步中的运算结果 15 与 7 相乘 , 得到 105 ;另法:第1步使 s = 1 ;第2步使 n = 3 ;第3步第4步第5步若 n ? 7 返回第 3 步 , 否则输出 s .解 :练习3.已知直角坐标系中的两点A( - 1 , 0 ),B( 3 , 2 ) , 写出求直线 AB 的方程的一个算法 .第1步第2步用点斜式写出直线方程 y – 0 = k AB ( x + 1 ) .解 :练习4.写出求 1 + 2 + 3 + ··· + 100 的一个算法 .第1步取 n = 100 ;第2步第3步输出运算结果.另法:第1步使 s = 1 ;第2步使 n = 2 ;第3步第4步第5步若 n ? 100 返回第 3 步 , 否则输出 s .解 :5.2 流 程 图 引例:？S1取 n 等于 1 ;S2S3YN输入 n﹥2005输出 n结束表示输入输出操作 ,一般画成平行四边形 ( 输入输出框 ) ; 表示处理和运算 , 通常画成矩形( 处理框 ) ; 表示执行步骤的路径,可用箭头表示( 流程线 ) ; 根据条件决定执行两条路径中的某一条 , 一般画成菱形 ( 判断框 ) ; 表示算法的开始或结束 ,常用圆角矩形表示 ( 起止框 ) . 5.2.1 顺 序 结 构 引例:写出作 ? ABC 的外接圆的一个算法.S1作 AB 的垂直平分线 l 1 ;?l1S2作 BC 的垂直平分线 l 2 ;?l2?MS3以 l 1与 l 2 交点 M 为圆心 , MA为半径作圆 , 圆 M 即为所求 .像这种依次进行多个处理的结构称为顺序结构.例1. 已知两个单元分别存放了变量 x 和 y 的值 , 试交换这两个变量值 .S1S2x yS3 y P 解 :例2. 半径为r的圆的面积计算公式为 S = ? r 2 , 当 r = 10 时 , 写出计算圆面积的算法 , 画出流程图 .S1S2S3输出 S .输出 S 解 :练习1.写出作棱长为 2 的正三棱柱的直观图的算法 .S1x ’y ’Oz ’S2S3A’B’C’S4练习2.S1S2S3将上面的方程组自下而上回代求解 , 从而得出 x = 1 , y = 2 , z = 3 .消去第 2 、第 3 个方程中的 x消去第 3 个方程中的 y方程组自下而上回代求得 x , y , z5.2.2 选 择 结 构 引例:某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为其中 w ( 单位 : kg ) 为行李的重量 , 试给出计算费用 c ( 单位 : 元 )的一个算法 .S1输入行李的重量w ;S2若 w ? 50 , 则 c = 0 . 35 × w ,否则 c = 50 × 0 . 35 + ( w – 50 ) × 0 . 85 ;S3输出行李的重量 w 和运费 c .输入w w ? 50 Y输出 w , cN输出 w , c 像这种先根据条件作出判断 , 再决定执行哪一种操作的结构称为选择结构 . 例3.设计求解一元二次方程 a x 2 + b x + c = 0 ( a ≠ 0 ) 的一个算法 , 并用流程图表示 .S1输入 a , b , c ;S2S3如果 ?＜0 为真 , 则输出“ 方程无实数根 ” , 否则 输入 a , b , c ?＜0Y输出“ 方程无实数根 ” N结 束输出 x1 , x2解 :思考: 设计求解方程 a x 2 + b x + c = 0 的一个算法 , 并用流程图表示 .输入 a , b , c ?＜0Y输出“ 无实根 ” N结 束输出 x1 , x2a = 0Yb = 0Yc = 0Y输出“ 解为全体实数 ” NN输出 x N输出 无解 练习1.如果考生的成绩大于或等于 60 分 , 则输出“及格”,否则输出“不及格” , 用流程图表示这一算法过程 .考生学号和成绩成绩 ? 60Y输出学号和“不及格” 结 束 N输出学号和“及格” 解 :练习2.下面的流程图表示了一个什么样的算法 ?输入 a , b , c a ? b 且 a ? cY输出 a Nb ? c*Y输出 bN输出 c所给流程图描述了求三个数 a , b , c 的最大数的算法 .练习3. 写出解方程 a x + b = 0 ( a , b 为常数 ) 的一个算法 , 并画出流程图.输入 a , b a = 0Yb = 0Y输出“ 解为全体实数 ” 结 束N输出“ 无解 ” N输出 x 解 :5.2.3 循 环 结 构 引例: 北京获得了2008年第29界奥林匹克运动会主办权 , 你知道在申办的最后阶段 , 国际奥委会是如何通过投票决定主办权归属的吗 ? 对遴选的 5 个申办城市进行表决的操作程序是 : 首先进行第一轮投票 , 如果有一个城市得票超过总票数的一半 , 那么该城市将获得举办权 ; 如果所有申办城市得票数都不超过总票数的一半 , 则将得票数最少的城市淘汰 , 然后重复上述过程 , 直到选出一个申办城市为止 .S1投票 ;S2统计票数,如果有一个城市得票数超过总票数的一半,那么该城市就获得主办权 , 转 S3 , 否则淘汰得票数最少的城市 , 转 S1 ;S3宣布主办城市 .开 始投 票有一个城市得票数超过总票数的一半Y输出该城市结 束N像这种需要重复执行同一操作的结构称为 循环结构.例4. 写出求 1 ? 2 ? 3 ? 4 ? 5 值的一个算法 .算法1 .S1先求 1 ? 2 , 得到 2 ; S2将 S1 得到的结果再乘以 3 , 得到 6 ; S3将 S2 得到的结果 6 再乘以 4 , 得到 24 ; S4将 S3 得到的结果 24 再乘以 5 , 得到 120 . 算法2 .S1S2S3S4S5如果 I 不大于 5 , 返回重新执行步骤 S3 及 S4 , S5 , 否则算法结束 . I ? 5Y结 束 N解 :例5. 设计一个计算10个数平均数的算法.S1S2S3输入 G ;S4S5S6如果 I 不大于 10 , 转到 S3 ;S7S8输出 A .输入 G I ? 10Y输出 AN解 :练习1.先分步写出计算 2 + 4 + 6 + ··· + 100 的一个算法 ,再画出流程图 .S1S2S3S4S5如果 I ? 100 , 转到 S3 , 否则输出S .I ? 100Y输出 SN解 :练习2.用 N i 代表第 i 个学生的学号 , G i 代表第 i 个学生的成绩 ( i = 1 , 2 , 3 , ··· , 50 ) , 那么下图表示了一个什么样的算法 ?G i ? 80Y打印 N i , G i i ? 50 YN结 束 N流程图表示将 50 个成绩不低于 80 分的学生打印出来 .解 :5.3 基 本 算 法 语 句 算法是一种数学语言,如何用更简捷的语句表述算法语言呢? 伪代码是介于自然语言和计算机语言之间的文字和符号,是表达算法的简单而实用的好方法.5.3.1 赋 值 语 句例1.写出求 x = 23 时多项式 7 x 3 + 3 x 2 – 5 x + 11 的值的算法 .算 法 1 :算 法 2 :解 :5.3.2 输 入 、输 出 语 句“ 鸡兔同笼 ” 是我国隋朝时期的数学著作《 孙子算经 》中的一个有趣而具有深远影响的题目 :“ 今有雏兔同笼,上有三十五头,下有九十四足.问雏兔各几何. ” 设有 x 只鸡 , y 只兔 , 则 用方程组的思想不难解决这一问题 . 下面我们设计一个解二元一次方程组的通用算法 . 因此,只要输入相应的未知数的系数和常数项 , 就能计算出方程组的解 , 即可以输出 x , y 的值 . 我们用输入语句 “ Read a , b ” 表示输入的数据依此送给 a , b , 用输出语句 “ Print x ” 表示输出运算结果 x .输入 a 1 , b 1 , c 1 , a 2 , b 2 , c2输出 x , yRead a 1 , b 1 , c 1 , a 2 , b 2 , c2Print x , y练习1. 已知一个正三棱柱的底面边长为 2 , 高为 3 , 用输入 、输出语句和赋值语句表示计算此三棱柱体积的算法 .Read a , h ( a = 2 , h = 3 )Print a , b , c解 :练习2. 若三角形的三边长分别为 a , b , c ,借助三角形的面积公式 用输入 、输出语句和赋值语句表示计算三角形面积的一种算法 .Read a , b , c Print S解 :练习3. 某市2003年1~12月的产值分别为 3.8 , 4.2 , 5.3 , 6.1 , 5.6 , 4.8 , 7.3 , 4.5 , 6.4 , 5.8 , 4.7 , 6.5 ( 亿元 ) , 该市要统计每季度的月平均产值及2003年的月平均产值 , 试分别用赋值语句和输入输出语句表示计算上述各个平均值的算法.Read p1 , p2 , p3 , p4 , p5 , p6 , p7 , p8 , p9 , p10 , p11 , p12 Print A , B ,C , D , E解 :5.3.3 条 件 语 句 某居民区的物业管理部门每月按以下方法收取卫生费 : 3 人和 3 人以下的住户 , 每户收取 5 元 ; 超过 3 人的住户 , 每超出 1 人加收 1 . 2 元 .如何设计算法 , 根据输入的人数计算应收取的卫生费 ? 我们令 c ( 单位 : 元 ) 表示应收取的费用 . t 表示这户人家的人口数 , 则有解决这一问题的算法步骤如下 : S1输入 人数 t ;S2S3输出 c .Read tEnd ifPrint c输入 tt ? 3Y结 束 N 从流程图可以看出这是一个选择结构 , 我们可运用条件语句来实现上述过程 . 条件语句的一般形式是If A then B Else CEnd if例2.儿童乘坐火车时 , 若身高不超过 1.1 m , 则无需购票 ; 若身高超过 1.1 m 但不超过 1.4 m , 可买半票 ; 若身高超过 1.4 m , 应买全票 . 试设计一个购票的算法 , 写出伪代码 , 并画出流程图 .解 :上述购票的算法步骤为 :S1测量儿童的身高 h ;S2如果 h ? 1.1 ,那么免费乘车 ;否则,如果 h ? 1.4 ,那么购半票乘车;否则 , 购买全票乘车.用条件语句表示为 :Read hIf h ? 1.1 then Print 免费乘车Else if h ? 1.4 thenPrint 半票乘车Else Print 全票乘车End if流程图如下图所示 :输入 hh ? 1.1Y 免费乘车结 束 Nh ? 1.4Y 半票乘车N 全票乘车解 :用条件语句可以方便地表示这类分段函数 :Read xIf x ? 0 then Else if x = 0 thenElse End ifPrint y输入 xx ? 0Y输出 y Nx = 0YN练习1.用条件语句表示 : 输入两个数 , 打印较大的数 . Read a , b If a ? b thenPrint a Else Print b End if解 :练习2.Read xIf x ? 0 then Else End ifPrint y 解 :练习3. 到银行办理个人异地汇款 ( 不超过 100 万 ) 时 , 银行要收取一定的手续费 , 汇款额不超过 100 元 , 收取 1 元手续费 ; 超过 100 元但不超过 5000 元 , 按汇款额的 1 % 收取 ; 超过5000 元 , 一律收取 50 元手续费 . 试用条件语句描述汇款额为x ( 元 ) 时 , 求银行收取的手续费 y ( 元 ) 的算法过程 , 并画出流程图 . Read x ( x ? 1 000 000 )If x ? 100 then Else if x ? 5000 thenElse End ifPrint y 输入 xx ?100Y输出 y Nx?5000YN解 :5.3.4 循 环 语 句设计计算 1 × 3 × 5 × 7 × ··· × 99 的一个算法 .解 :S1S2S3S4S5如果 I ? 99 , 那么转到 S3 .S6输出 S .I ? 99N输出 SY 从流程图可以看出这是一个循环结构 , 我们可以运用循环语句来实现上述过程 . 当循环的次数已经确定,可用 “ For ” 语句表示 . “ For ”语句的一般形式为 : For I from “ 初值 ” to “ 终值 ” step “ 步长 ” ··· End for上述问题用循环语句表示为 :For I from 3 to 99 step 2 End forPrint S 上面 “ For ” 和 “ End for ” 之间缩进的步骤称为循环体 . 如果省略 “ step 2 ” , 那么重复循环时 , I 的值每次增加 1 .那么 , 如何寻找满足条件的最小整数呢 ?算法步骤如下 :S1S2S3S4输出 I . 当循环次数不能确定时 , 可用 “ While ” 语句来实现循环 . “ While ” 语句的一般形式为 : While A · · · End while 其中 A 表示判断执行循环的条件. 前面的问题用 “ While ” 语句可描述如下 : While S ? 10000 End while Print I 上面 “ While ” 和 “ End while ” 之间缩进的步骤称为循环体 . “ While ” 语句的特点是 “ 前测试 ” , 即先判断 , 后执行 . 若初始条件不成立 , 则一次也不执行循环体中的内容 . 任何一种需要重复处理的问题都可以用这种前测试循环来实现 .例4.抛掷一枚硬币时,既可能出现正面 , 也可能出现反面 , 预先作出确定的判断是不可能的 , 但是假如硬币质量均匀 , 那么当抛掷次数很多时 , 出现正面的频率应接近于 50 % . 试设计一个循环语句模拟抛掷硬币的过程 , 并计算抛掷中出现正面的频率 .解 :Read n For i from 1 to n Next i练习1 .试用 “ While ” 语句描述这一问题的算法过程 .解 : While S ? 2004 End while Print I练习2 .2000年我国人口数约为 13 亿 . 如果每年的人口自然增长率为 15 ‰ , 那么多少年后我国人口将达到或超过 15 亿 ? 这个问题可通过循环方式计算完成 , 即每一次在原有的基础上增加 15 ‰ , 直到达到或超过 15 亿 , 再记下循环次数 .试用循环语句表示这一过程 .解 : While P ? 15 End while Print n练习3.根据下图,用条件语句和循环语句描述该算法过程.输入 a,b,c a ? b 且 a ? cY输出a Nb ? cY输出 bN输出 cRead a , b , c If a ? b 且 a ? c then Print aElse if b? c thenPrint bElse Print cEnd if练习4.1 , 1 , 2 , 3 , 5 , 8 , 13 , ··· 这一列数的规律是 : 第 1 、第 2 个数是 1 , 从第 3 个数起 , 该数是其前面两个数之和 . 试用循环语句描述计算这列数中前 20 个数之和的算法 .解 : While n ? 20 End while Print S习 题 5 . 1解 :S1输入 a = 7.28 , h = 14.29 ;S2S3输出 S .输入 a = 7.28 , h = 14.29 输出 S 2 . 火车站对乘客在一定时段内退票要收取一定的费用 , 收费的办法是 : 按票价每 10 元 ( 不足 10 元按 10 元计算 ) 核收 2 元 , 2 元以下的票价不退 . 试分步写出将票价为 x 元的火车票退掉后 , 返还的金额 y 的算法 , 并画出流程图 .解 :S1输入票价 x ;S2如果 x ? 2 , 那么 y = 0 , S3输出返还金额 y .输入票价 x x ? 2 Y y = 0 NYN输出 y m = 4 ? 2( 2 ) - ( 1 ) × m回代求解得x = 1 ,y = 1 4 . 画出求两个正整数 a 与 b 相除所得商 q 及余数 r 的一个算法的流程图.输入 a , b 输出 r , q 5 . 写出一个求三个实数中最小数的算法 , 并画出流程图 .S1解 :输入 a , b , c ; S2S3S4S5输出最小数 m . 输入 a , b , c b ? m YN c ? m YN输出 m 6 . 写出解不等式 a x + b ? 0 ( a ? 0 ) 的一个算法 , 并画出流程图 .解 :S1输入 a , b ; S2S3如果 a ? 0 ,那么输出 x ? x0 ; 否则输出 x ? x0 . 输入 a , b a ? 0 Y输出 x ? x0 结 束N输出 x ? x0 解 :S1S2S3S4如果 I 不大于 6 ,那么转到S 2 ; S5输出 S . I ? 6 Y输出 S N 8 . 写出在数 3 , 5 , 8 , 9 , 12 , 15 , 35 , 7 , 18 , 52 中搜索数 18 的一个算法 , 并画出流程图 .解 :输入 n n =18 Y输出 n N输入 a , b , c a + b ? c 且 b + c ? a 且 c + a ? b Y输出 S结 束N输出 “ 不能构成三角形 ”