算法讲座[上学期]
图片预览











文档简介
课件53张PPT。算 法算法的含义顺序结构选择结构循环结构赋值语句输入输出语句条件语句循环语句算法案例流程图基本语句算法的含义把大象装进冰箱里,需要哪几步?把长颈鹿装进冰箱里需要哪几步? 求下列各三角函数的值: 求任意角的正弦或余弦的一般方法.广义地说:
为了解决某一问题而采取的方法和步骤,
我们称之为算法.用S1代表步骤1,S2代表步骤2,以此类推. 给出用配方法解方程
x2-2x-3=0的一个算法.典型问题: 给出解方程组
的一个算法.一般而言:
对一类问题的机械的,统一的求解方法称为算法.广义地说:
为了解决某一问题而采取的方法和步骤,
我们称之为算法. 对于输入的正整数n,求
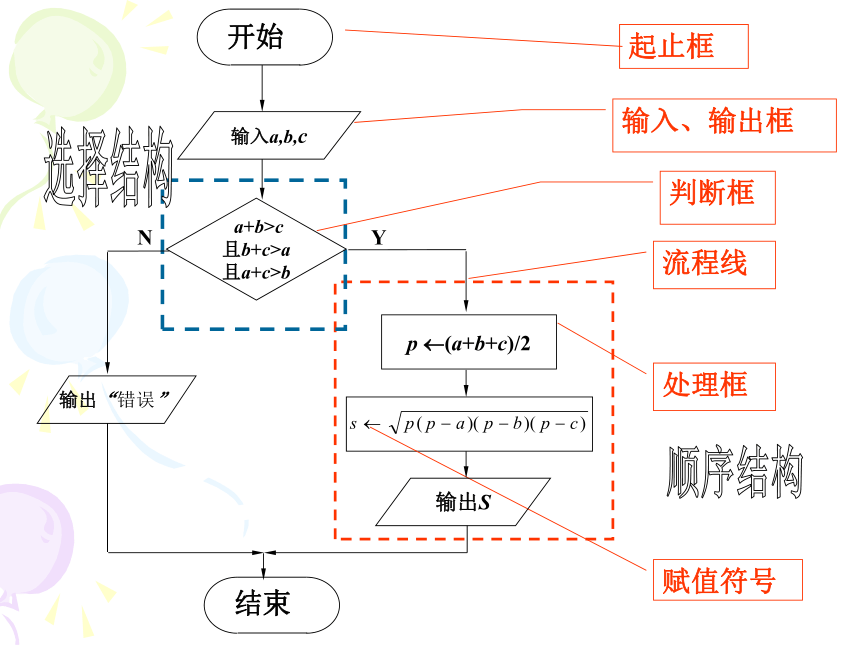
1+2+3+…+n. 请设计一个算法,计算输入实数的绝对值.流程图起止框流程线输入、输出框处理框顺序结构选择结构赋值符号判断框顺序结构选择结构 △<0YN开始结束△=0YN △<0YN输出“方程无实数解”开始结束循环结构写出1+2+3+…+5的一个算法
S1 n?5;
S2 S? n(n+1)/2;
S3 输出S.结束输出SS ← 0开始i ← i + 1S ← S + ii>5NYi ← 10+1=1 1+1=2
1+2=3 2+1=3
3+3=6 3+1=4
6+4=10 4+1=5
10+5=15 5+1=6S←S+i i← i+1
S←S+i i← i+1
S←S+i i← i+1
S←S+i i← i+1
S←S+i i← i+1结束输出SS ← 0开始i ← i + 1S ← S + ii≥5NYi ← 00+1=1 0+1=1
1+1=2 1+2=3
2+1=3 3+3=6
3+1=4 6+4=10
4+1=5 10+5=15i← i+1 S←S+i
i← i+1 S←S+i
i← i+1 S←S+i
i← i+1 S←S+i
i← i+1 S←S+i 结束输出SS ← 0开始i ← i + 1S ← S + ii>5NYi ← 1结束输出SS ← 0开始i ← i + 1S ← S + ii≥5NYi ← 0前计数后计数如果循环次数确定,一般主张后计数.i的作用就是计数.为什么要从0开始加?一般要求累加器清零.S的作用就是累加.S ← 0开始i≤5i ← 1YN结束输出Si ← i + 1S ← S + iS ← 0开始i≤5i ← 1YN结束输出Si ← i + 1S ← S + i写出1×2×3×4×5×…×50的一个算法.写出1×2×3×4×5×…×50的一个算法.算法语句条件语句Read x
If x<0 Then
y←-x
Else
y←x
End If
Print xRead x
If x>0 Then
y←1
Else If x=0 Then
y←0
Else
y←-1
End If
Print yS←0
i←1
While i ≤5
S←S+i
i ← i+1
End While
Print S1+2+3+…+_________>2004.S←1
i←1
While S≤2004
i ← i+1
S←S+i
End While
Print iS←0
i←1
While i ≤5
S←S+i
i ← i+1
End While
Print SS←0
For i From 1 To 5 step 1
S←S+i
End For
Print S算法案例孙子问题 在我国古代算书《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”m ? 2
While Mod (m,3)≠2 或
Mod (m,5)≠3 或
Mod (m,7)≠2
m ? m+1
End While
Print m最大公约数问题总体构想18的约数:1,2,3,6,9,18.
30的约数,1,2,3,5,6,10,15,30.搜索总体构想你准备从a开始搜索,还是从b开始搜索?你准备从小到大搜索,还是从大到小搜索?输入两个正整数a,b(a>b)你能保证循环次数是有限次吗?执行循环的条件是什么?Read a,b
i=b
While Mod(a,i) ≠0或 Mod(b,i) ≠0
i=i-1
End While
Print i 204=85×2+34
从这一步说明,204与85的最大公约数也应该是85与34的最大公约数.
85=34×2+17
从这一步说明,85与34的最大公约数也应该是34与17的最大公约数.
34=17×2
从这一步说明,34与17的最大公约数就是17.
所以204与85的最大公约数是17. 8251=6105+2146;
6105=2146×2+1813;
2146=1813+333;
1813=333×5+148;
333=148×2+37;
148=37×4,
所以8251与6105的最大公约数是37.求8251和6105的最大公约数. 204=85×2+34 ;
85=34×2+17 ;
34=17×2.8251=6105+2146;
6105=2146×2+1813;
2146=1813+333;
1813=333×5+148;
333=148×2+37;
148=37×4.Mod(a,b)请给出算法的流程图输入两个正整数a,b(a>b)开始结束输入a,bMod(a,b) ≠0a←bb←Mod(a,b)YN输出b开始结束输入a,bMod(a,b) ≠0a←bb←Mod(a,b)YN输出bRead a,b
While Mod(a,b) ≠0
r←Mod(a,b)
a←b
b←r
End While
Print b二分法问题:写出用区间二分法求方程x3-x-1=0在区间[1,1.5]内的一个近似解(误差不超过
0.001)的一个算法.
为了解决某一问题而采取的方法和步骤,
我们称之为算法.用S1代表步骤1,S2代表步骤2,以此类推. 给出用配方法解方程
x2-2x-3=0的一个算法.典型问题: 给出解方程组
的一个算法.一般而言:
对一类问题的机械的,统一的求解方法称为算法.广义地说:
为了解决某一问题而采取的方法和步骤,
我们称之为算法. 对于输入的正整数n,求
1+2+3+…+n. 请设计一个算法,计算输入实数的绝对值.流程图起止框流程线输入、输出框处理框顺序结构选择结构赋值符号判断框顺序结构选择结构 △<0YN开始结束△=0YN △<0YN输出“方程无实数解”开始结束循环结构写出1+2+3+…+5的一个算法
S1 n?5;
S2 S? n(n+1)/2;
S3 输出S.结束输出SS ← 0开始i ← i + 1S ← S + ii>5NYi ← 10+1=1 1+1=2
1+2=3 2+1=3
3+3=6 3+1=4
6+4=10 4+1=5
10+5=15 5+1=6S←S+i i← i+1
S←S+i i← i+1
S←S+i i← i+1
S←S+i i← i+1
S←S+i i← i+1结束输出SS ← 0开始i ← i + 1S ← S + ii≥5NYi ← 00+1=1 0+1=1
1+1=2 1+2=3
2+1=3 3+3=6
3+1=4 6+4=10
4+1=5 10+5=15i← i+1 S←S+i
i← i+1 S←S+i
i← i+1 S←S+i
i← i+1 S←S+i
i← i+1 S←S+i 结束输出SS ← 0开始i ← i + 1S ← S + ii>5NYi ← 1结束输出SS ← 0开始i ← i + 1S ← S + ii≥5NYi ← 0前计数后计数如果循环次数确定,一般主张后计数.i的作用就是计数.为什么要从0开始加?一般要求累加器清零.S的作用就是累加.S ← 0开始i≤5i ← 1YN结束输出Si ← i + 1S ← S + iS ← 0开始i≤5i ← 1YN结束输出Si ← i + 1S ← S + i写出1×2×3×4×5×…×50的一个算法.写出1×2×3×4×5×…×50的一个算法.算法语句条件语句Read x
If x<0 Then
y←-x
Else
y←x
End If
Print xRead x
If x>0 Then
y←1
Else If x=0 Then
y←0
Else
y←-1
End If
Print yS←0
i←1
While i ≤5
S←S+i
i ← i+1
End While
Print S1+2+3+…+_________>2004.S←1
i←1
While S≤2004
i ← i+1
S←S+i
End While
Print iS←0
i←1
While i ≤5
S←S+i
i ← i+1
End While
Print SS←0
For i From 1 To 5 step 1
S←S+i
End For
Print S算法案例孙子问题 在我国古代算书《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”m ? 2
While Mod (m,3)≠2 或
Mod (m,5)≠3 或
Mod (m,7)≠2
m ? m+1
End While
Print m最大公约数问题总体构想18的约数:1,2,3,6,9,18.
30的约数,1,2,3,5,6,10,15,30.搜索总体构想你准备从a开始搜索,还是从b开始搜索?你准备从小到大搜索,还是从大到小搜索?输入两个正整数a,b(a>b)你能保证循环次数是有限次吗?执行循环的条件是什么?Read a,b
i=b
While Mod(a,i) ≠0或 Mod(b,i) ≠0
i=i-1
End While
Print i 204=85×2+34
从这一步说明,204与85的最大公约数也应该是85与34的最大公约数.
85=34×2+17
从这一步说明,85与34的最大公约数也应该是34与17的最大公约数.
34=17×2
从这一步说明,34与17的最大公约数就是17.
所以204与85的最大公约数是17. 8251=6105+2146;
6105=2146×2+1813;
2146=1813+333;
1813=333×5+148;
333=148×2+37;
148=37×4,
所以8251与6105的最大公约数是37.求8251和6105的最大公约数. 204=85×2+34 ;
85=34×2+17 ;
34=17×2.8251=6105+2146;
6105=2146×2+1813;
2146=1813+333;
1813=333×5+148;
333=148×2+37;
148=37×4.Mod(a,b)请给出算法的流程图输入两个正整数a,b(a>b)开始结束输入a,bMod(a,b) ≠0a←bb←Mod(a,b)YN输出b开始结束输入a,bMod(a,b) ≠0a←bb←Mod(a,b)YN输出bRead a,b
While Mod(a,b) ≠0
r←Mod(a,b)
a←b
b←r
End While
Print b二分法问题:写出用区间二分法求方程x3-x-1=0在区间[1,1.5]内的一个近似解(误差不超过
0.001)的一个算法.
