5.3-5.4平行线的性质、平移 同步测试(含答案)
文档属性
| 名称 | 5.3-5.4平行线的性质、平移 同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-21 11:42:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
七年级下册数学 5.3-5.4平行线的性质、平移 同步测试
时间:45分钟 满分:100分
一、选择题(每小题4分,共32分)
1.下列命题中,是真命题的是( )
A.过一点有且只有一条直线与已知直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.在同一平面内,垂直于同一直线的两条直线平行
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17
3.如图,△ABC沿BC方向平移到△DEF的位置,若BE=2cm,则平移的距离为( )
A.1 B.2 C.3 D.4
4.如图,∠1=70°,直线a平移后得到直线b,则∠2的度数比∠3的度数大( )
A.70° B.80° C.110° D.180°
5.如图,已知AB∥CD,能判断BE∥CF的条件是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.∠1=∠2
6.如图,直线,直线交于点A,交于点B,过点B的直线交于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A.80° B.70° C.60° D.50°
7.如图,DC∥EF∥AB,EH∥DB,则图中与∠AHE相等的角有( )
A.3个 B.4个 C.5个 D.6个
8.如图,AB∥CD,则∠A,∠C,∠E,∠F满足的数量关系是( )
A.∠A=∠C+∠E+∠F B.∠A+∠E-∠C-∠F=180°
C.∠A-∠E+∠C+∠F=90° D.∠A+∠E+∠C+∠F=360°
二、填空题(每小题5分,共25分)
9.把命题“邻补角互补”改写成“如果……,那么……”的形式: .
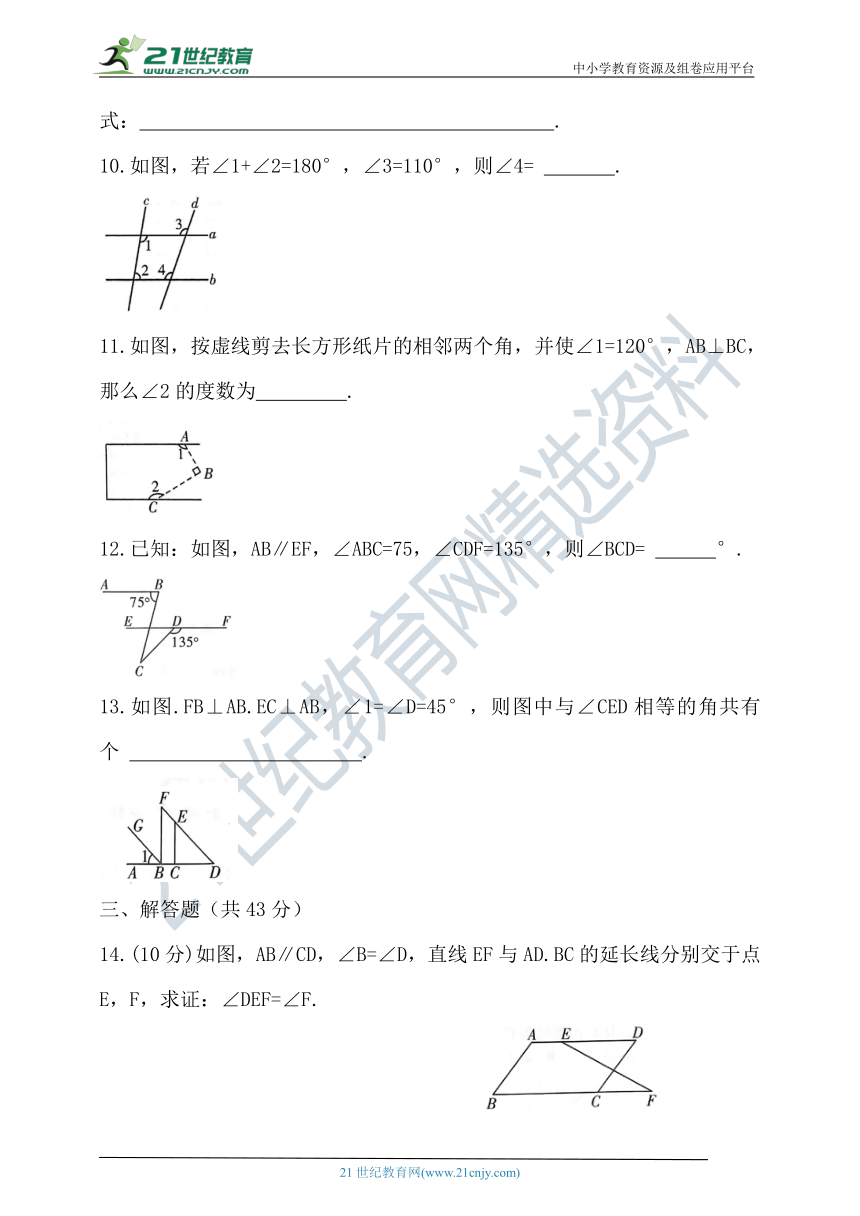
10.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
11.如图,按虚线剪去长方形纸片的相邻两个角,并使∠1=120°,AB⊥BC,那么∠2的度数为 .
12.已知:如图,AB∥EF,∠ABC=75,∠CDF=135°,则∠BCD= °.
13.如图.FB⊥AB.EC⊥AB,∠1=∠D=45°,则图中与∠CED相等的角共有个 .
三、解答题(共43分)
14.(10分)如图,AB∥CD,∠B=∠D,直线EF与AD.BC的延长线分别交于点E,F,求证:∠DEF=∠F.
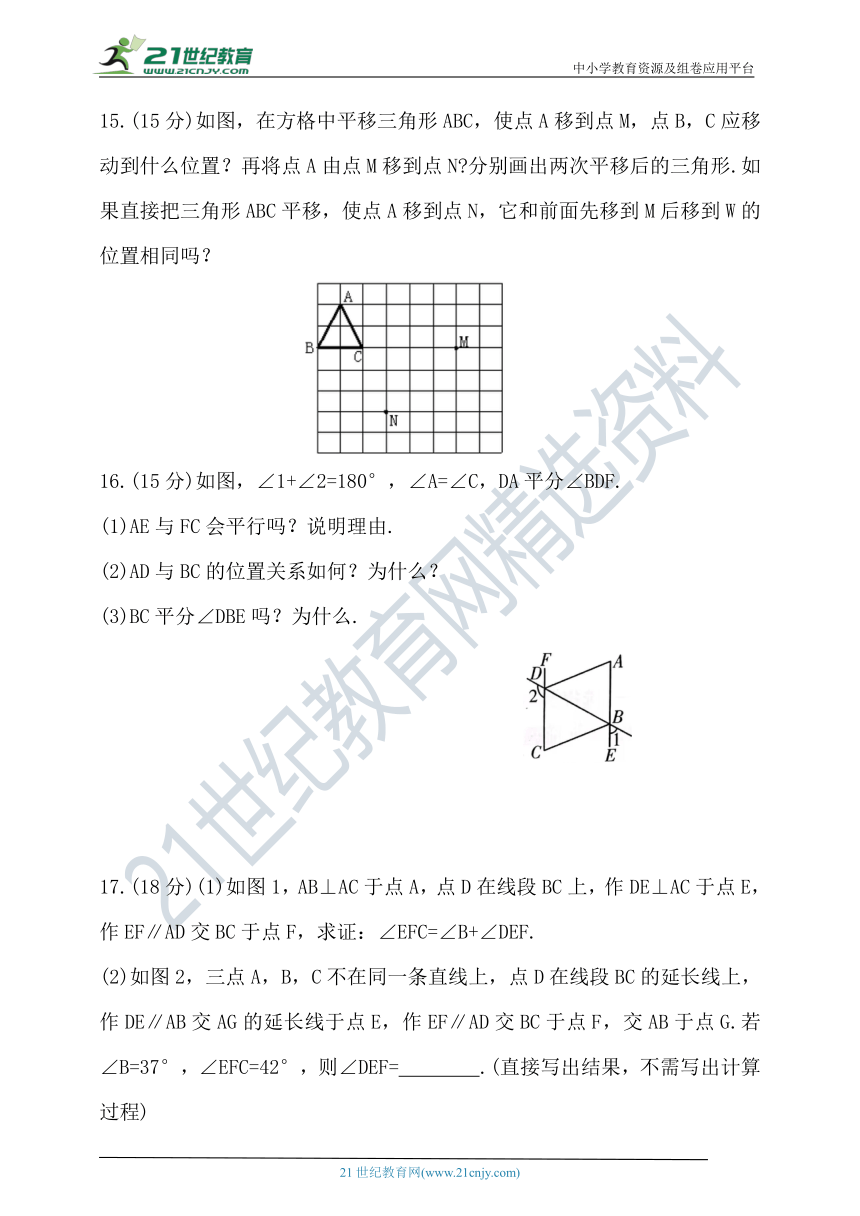
15.(15分)如图,在方格中平移三角形ABC,使点A移到点M,点B,C应移动到什么位置?再将点A由点M移到点N 分别画出两次平移后的三角形.如果直接把三角形ABC平移,使点A移到点N,它和前面先移到M后移到W的位置相同吗?
16.(15分)如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
17.(18分)(1)如图1,AB⊥AC于点A,点D在线段BC上,作DE⊥AC于点E,作EF∥AD交BC于点F,求证:∠EFC=∠B+∠DEF.
(2)如图2,三点A,B,C不在同一条直线上,点D在线段BC的延长线上,作DE∥AB交AG的延长线于点E,作EF∥AD交BC于点F,交AB于点G.若∠B=37°,∠EFC=42°,则∠DEF= .(直接写出结果,不需写出计算过程)
参考答案
1.D 2.C 3.B 4.C 5.C 6.B 7.C 8.B
9.如果两个角是邻补角,那么它们(这两个角)互补
10.110° 11.150° 12.30 13.4
I4.证明:∵AB∥CD,∴∠DCF=∠B.∵∠B=∠D,∴∠DCF=∠D.
∴AD∥BC. ∴∠DEF=∠F
15.解:如图所示,直接把△ABC平移.使点A移到点N.它和前面先移到M后移到N的位置相同.
16.解:(1)平行,理由如下:
∵∠1+∠2=180°,∠2+∠CDB=180(邻补角定义),
∴∠1=∠CDB.∴AE∥FC(同位角相等,两直线平行,
(2)平行.理由如下:∵AE∥CF,
∴∠C=∠CBE(两直线平行,内错角相等)
又∠A=∠C.∴∠A=∠CBE
∴AD∥BC(同位角相等,两直线平行)
(3)平分.理由如下:
∵DA平分∠BDF,∴∠FDA=∠ADB
∵AE∥CF,AD ∥BC.
∴∠FDA=∠A=∠CBE,∠ADB=∠CBD
∴∠CBE=∠CBD.即BC平分∠DBE
17.证明:(1)∵AB⊥AC,DE⊥AC,
∴∠BAC=∠DEC=90°.
∴AB∥DE.∴∠BHD=∠ADE.
∵EF//AD,∴∠ADE=∠DEF,∠EFC=∠ADC
∵∠ADC+∠BDA=∠B+∠BAD+∠BDA,
∴∠ADC=∠B+∠BAD.∴∠EFC=∠B+∠DEF.
(2)101°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级下册数学 5.3-5.4平行线的性质、平移 同步测试
时间:45分钟 满分:100分
一、选择题(每小题4分,共32分)
1.下列命题中,是真命题的是( )
A.过一点有且只有一条直线与已知直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.在同一平面内,垂直于同一直线的两条直线平行
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17
3.如图,△ABC沿BC方向平移到△DEF的位置,若BE=2cm,则平移的距离为( )
A.1 B.2 C.3 D.4
4.如图,∠1=70°,直线a平移后得到直线b,则∠2的度数比∠3的度数大( )
A.70° B.80° C.110° D.180°
5.如图,已知AB∥CD,能判断BE∥CF的条件是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.∠1=∠2
6.如图,直线,直线交于点A,交于点B,过点B的直线交于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A.80° B.70° C.60° D.50°
7.如图,DC∥EF∥AB,EH∥DB,则图中与∠AHE相等的角有( )
A.3个 B.4个 C.5个 D.6个
8.如图,AB∥CD,则∠A,∠C,∠E,∠F满足的数量关系是( )
A.∠A=∠C+∠E+∠F B.∠A+∠E-∠C-∠F=180°
C.∠A-∠E+∠C+∠F=90° D.∠A+∠E+∠C+∠F=360°
二、填空题(每小题5分,共25分)
9.把命题“邻补角互补”改写成“如果……,那么……”的形式: .
10.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
11.如图,按虚线剪去长方形纸片的相邻两个角,并使∠1=120°,AB⊥BC,那么∠2的度数为 .
12.已知:如图,AB∥EF,∠ABC=75,∠CDF=135°,则∠BCD= °.
13.如图.FB⊥AB.EC⊥AB,∠1=∠D=45°,则图中与∠CED相等的角共有个 .
三、解答题(共43分)
14.(10分)如图,AB∥CD,∠B=∠D,直线EF与AD.BC的延长线分别交于点E,F,求证:∠DEF=∠F.
15.(15分)如图,在方格中平移三角形ABC,使点A移到点M,点B,C应移动到什么位置?再将点A由点M移到点N 分别画出两次平移后的三角形.如果直接把三角形ABC平移,使点A移到点N,它和前面先移到M后移到W的位置相同吗?
16.(15分)如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
17.(18分)(1)如图1,AB⊥AC于点A,点D在线段BC上,作DE⊥AC于点E,作EF∥AD交BC于点F,求证:∠EFC=∠B+∠DEF.
(2)如图2,三点A,B,C不在同一条直线上,点D在线段BC的延长线上,作DE∥AB交AG的延长线于点E,作EF∥AD交BC于点F,交AB于点G.若∠B=37°,∠EFC=42°,则∠DEF= .(直接写出结果,不需写出计算过程)
参考答案
1.D 2.C 3.B 4.C 5.C 6.B 7.C 8.B
9.如果两个角是邻补角,那么它们(这两个角)互补
10.110° 11.150° 12.30 13.4
I4.证明:∵AB∥CD,∴∠DCF=∠B.∵∠B=∠D,∴∠DCF=∠D.
∴AD∥BC. ∴∠DEF=∠F
15.解:如图所示,直接把△ABC平移.使点A移到点N.它和前面先移到M后移到N的位置相同.
16.解:(1)平行,理由如下:
∵∠1+∠2=180°,∠2+∠CDB=180(邻补角定义),
∴∠1=∠CDB.∴AE∥FC(同位角相等,两直线平行,
(2)平行.理由如下:∵AE∥CF,
∴∠C=∠CBE(两直线平行,内错角相等)
又∠A=∠C.∴∠A=∠CBE
∴AD∥BC(同位角相等,两直线平行)
(3)平分.理由如下:
∵DA平分∠BDF,∴∠FDA=∠ADB
∵AE∥CF,AD ∥BC.
∴∠FDA=∠A=∠CBE,∠ADB=∠CBD
∴∠CBE=∠CBD.即BC平分∠DBE
17.证明:(1)∵AB⊥AC,DE⊥AC,
∴∠BAC=∠DEC=90°.
∴AB∥DE.∴∠BHD=∠ADE.
∵EF//AD,∴∠ADE=∠DEF,∠EFC=∠ADC
∵∠ADC+∠BDA=∠B+∠BAD+∠BDA,
∴∠ADC=∠B+∠BAD.∴∠EFC=∠B+∠DEF.
(2)101°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
