算法语言试题1[上学期]
图片预览

文档简介
高二第一次月考试题
《算法语言》
一、选择题
1、算法的有穷性是指
A.算法必须包含输出 B.算法中每个操作步骤都是可执行的
C.算法的步骤必须有限 C.以上说法均不正确
2、算法共有三种逻辑结构,即顺序结构,条件结构和循环结构,下列说法正确的是
A.一个算法只能含有一种逻辑结构 B. 一个算法最多可以包含两种逻辑结构
C. 一个算法必须含有上述三种逻辑结构 D. 一个算法可以含有上述三种逻辑结构的任意组合
3、下列给出的赋值语句中正确的是
A.4 = M B.M =-M
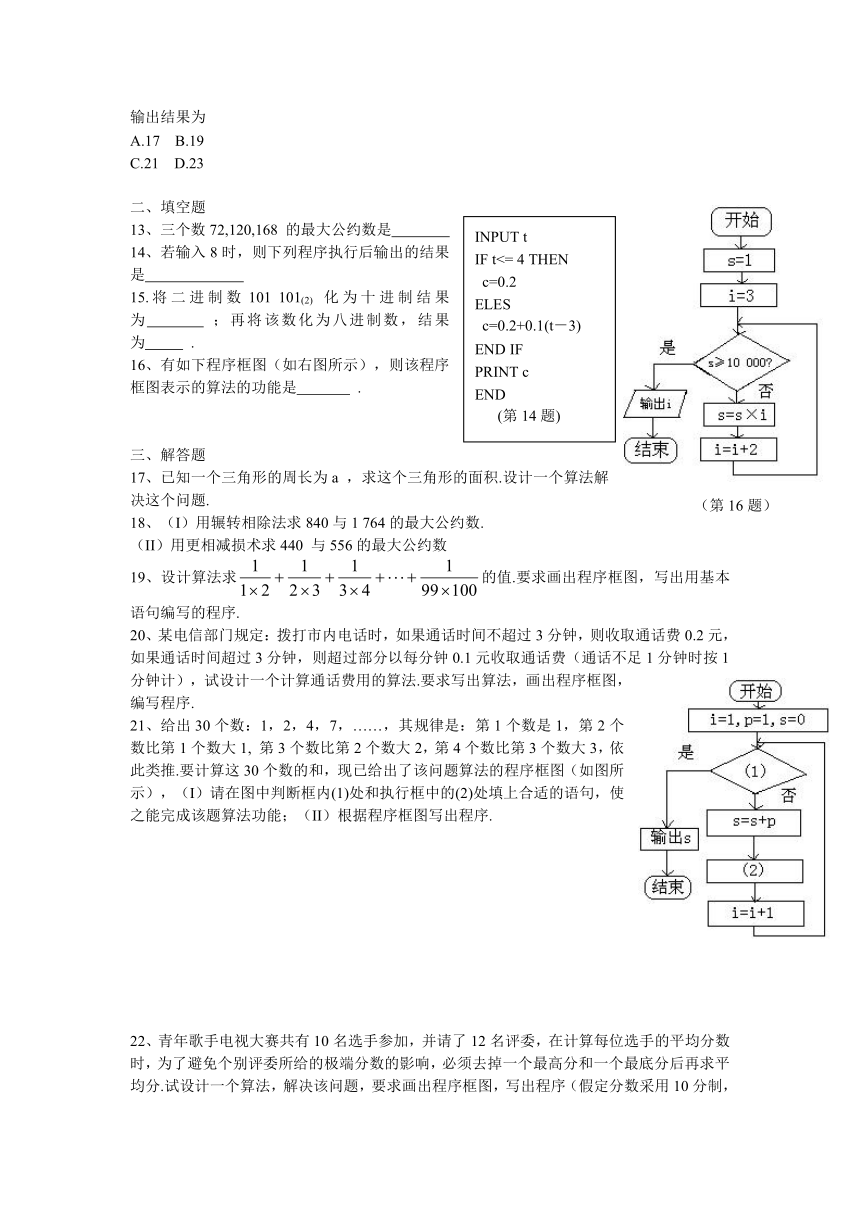
C.B=A-3 D.x + y = 0
4、右边程序执行后输出的结果是
A.-1 B.0 C.1 D2
5、以下给出的各数中不可能是八进制数的是
A.312 B.10 110 C.82 D.7 457
6、如果右边程序执行后输出的结果是132,那么
在程序until后面的“条件”应为
A.i > 11 B. i >=11 C. i <=11 D.i<11
7、840和1 764的最大公约数是
A.84 B.12 C.168 D.252
8、右图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是
A.i>10 B.i<10 C.i>20 D.i<20
9、右边程序运行的结果是
A.1,2,3 B.2,3,1 C.2,3,2 D.3,2,1
10.给出以下一个算法的程序框图(如图所示),该程序框图的功能是
A.求输出a,b,c三数的最大数
B. 求输出a,b,c三数的最小数
C.将a,b,c按从小到大排列
D. 将a,b,c按从大到小排列
11、右边的程序框图(如图所示),能判断任意输入的数x的奇偶性:
其中判断框内的条件是
A.m=0 B.x=0
C.x=1 D.m=1
12、右边程序运行后的输出结果为
A.17 B.19
C.21 D.23
二、填空题
13、三个数72,120,168 的最大公约数是
14、若输入8时,则下列程序执行后输出的结果是
15.将二进制数101 101(2) 化为十进制结果为 ;再将该数化为八进制数,结果为 .
16、有如下程序框图(如右图所示),则该程序框图表示的算法的功能是 .
三、解答题
17、已知一个三角形的周长为a ,求这个三角形的面积.设计一个算法解决这个问题.
18、(I)用辗转相除法求840与1 764的最大公约数.
(II)用更相减损术求440 与556的最大公约数
19、设计算法求的值.要求画出程序框图,写出用基本语句编写的程序.
20、某电信部门规定:拨打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元,如果通话时间超过3分钟,则超过部分以每分钟0.1元收取通话费(通话不足1分钟时按1分钟计),试设计一个计算通话费用的算法.要求写出算法,画出程序框图,编写程序.
21、给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个数比第1个数大1, 第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),(I)请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能;(II)根据程序框图写出程序.
22、青年歌手电视大赛共有10名选手参加,并请了12名评委,在计算每位选手的平均分数时,为了避免个别评委所给的极端分数的影响,必须去掉一个最高分和一个最底分后再求平均分.试设计一个算法,解决该问题,要求画出程序框图,写出程序(假定分数采用10分制,即每位选手的分数最高分为10分,最底分为0分).
第一章 算法初步参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
B
C
D
A
A
C
B
D
C
二、填空题 13. 24 14. 0.7 15. 45, 55(8)
16.计算并输出使1×3×5×7…× >10 000成立的最小整数.
17、算法步骤如下:
第一步,输入a的值;第二步,计算的值;第三步,计算的值;第四步,输出S的值.
18、解 (I)用辗转相除法求840与1 764 的最大公约数.
1 764 = 840×2 + 84 840 = 84×10 +0
所以840与1 764 的最大公约数是84
( II)用更相减损术求440 与556的最大公约数.
556-440 = 116 440-116 = 324 324-116 = 208 208-116 = 92 116-92 = 24
92-24 = 68 68-24 = 44 44-24 = 20 24-20 = 4 20-4 = 16
16-4 = 12 12-4 = 8 8-4 = 4
所以440 与556的最大公约数4.
19、解 这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下图所示
20、解 我们用c(单位:元)表示通话费,t(单位:分钟)表示通话时间,
则依题意有
算法步骤如下:第一步,输入通话时间t;第二步,如果t≤3,那么c = 0.2 ;否则令 c = 0.2+0.1 (t-3);
第三步,输出通话费用c ;
程序框图如图所示
21.解 (I)该算法使用了当型循环结构,因为是求30个数的和,故循环体应执行30次,其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为.算法 中的变量p实质是表示参与求和的各个数,由于它也是变化的,且满足第i个数比其前一个数大,,第个数比其前一个数大i,故应有.故(1)处应填;(2)处应填
(II)根据以上框图,可设计程序如下:
22、由于共有12位评委,所以每位选手会有12个分数,我们可以用循环语句来完成这12个分数的输入,同时设计累加变量求出这12个分数的和,本问题的关键在于从这12个输入分数中找出最大数与最小数,以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间,去我们可以先假设其中的最大数为0,最小数为10,然后每次输入一个评委的分数,就进行一次比较,若输入的数大于0,就将之代替最大数,若输入的数小于10,就用它代替最小数,依次下去,就能找出这12个数中的最大数与最小数,循环结束后,从总和中减去最大数与最小数,再除以10,就得到该选手最后的平均数.
程序框图如图所示.
《算法语言》
一、选择题
1、算法的有穷性是指
A.算法必须包含输出 B.算法中每个操作步骤都是可执行的
C.算法的步骤必须有限 C.以上说法均不正确
2、算法共有三种逻辑结构,即顺序结构,条件结构和循环结构,下列说法正确的是
A.一个算法只能含有一种逻辑结构 B. 一个算法最多可以包含两种逻辑结构
C. 一个算法必须含有上述三种逻辑结构 D. 一个算法可以含有上述三种逻辑结构的任意组合
3、下列给出的赋值语句中正确的是
A.4 = M B.M =-M
C.B=A-3 D.x + y = 0
4、右边程序执行后输出的结果是
A.-1 B.0 C.1 D2
5、以下给出的各数中不可能是八进制数的是
A.312 B.10 110 C.82 D.7 457
6、如果右边程序执行后输出的结果是132,那么
在程序until后面的“条件”应为
A.i > 11 B. i >=11 C. i <=11 D.i<11
7、840和1 764的最大公约数是
A.84 B.12 C.168 D.252
8、右图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是
A.i>10 B.i<10 C.i>20 D.i<20
9、右边程序运行的结果是
A.1,2,3 B.2,3,1 C.2,3,2 D.3,2,1
10.给出以下一个算法的程序框图(如图所示),该程序框图的功能是
A.求输出a,b,c三数的最大数
B. 求输出a,b,c三数的最小数
C.将a,b,c按从小到大排列
D. 将a,b,c按从大到小排列
11、右边的程序框图(如图所示),能判断任意输入的数x的奇偶性:
其中判断框内的条件是
A.m=0 B.x=0
C.x=1 D.m=1
12、右边程序运行后的输出结果为
A.17 B.19
C.21 D.23
二、填空题
13、三个数72,120,168 的最大公约数是
14、若输入8时,则下列程序执行后输出的结果是
15.将二进制数101 101(2) 化为十进制结果为 ;再将该数化为八进制数,结果为 .
16、有如下程序框图(如右图所示),则该程序框图表示的算法的功能是 .
三、解答题
17、已知一个三角形的周长为a ,求这个三角形的面积.设计一个算法解决这个问题.
18、(I)用辗转相除法求840与1 764的最大公约数.
(II)用更相减损术求440 与556的最大公约数
19、设计算法求的值.要求画出程序框图,写出用基本语句编写的程序.
20、某电信部门规定:拨打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元,如果通话时间超过3分钟,则超过部分以每分钟0.1元收取通话费(通话不足1分钟时按1分钟计),试设计一个计算通话费用的算法.要求写出算法,画出程序框图,编写程序.
21、给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个数比第1个数大1, 第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),(I)请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能;(II)根据程序框图写出程序.
22、青年歌手电视大赛共有10名选手参加,并请了12名评委,在计算每位选手的平均分数时,为了避免个别评委所给的极端分数的影响,必须去掉一个最高分和一个最底分后再求平均分.试设计一个算法,解决该问题,要求画出程序框图,写出程序(假定分数采用10分制,即每位选手的分数最高分为10分,最底分为0分).
第一章 算法初步参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
B
C
D
A
A
C
B
D
C
二、填空题 13. 24 14. 0.7 15. 45, 55(8)
16.计算并输出使1×3×5×7…× >10 000成立的最小整数.
17、算法步骤如下:
第一步,输入a的值;第二步,计算的值;第三步,计算的值;第四步,输出S的值.
18、解 (I)用辗转相除法求840与1 764 的最大公约数.
1 764 = 840×2 + 84 840 = 84×10 +0
所以840与1 764 的最大公约数是84
( II)用更相减损术求440 与556的最大公约数.
556-440 = 116 440-116 = 324 324-116 = 208 208-116 = 92 116-92 = 24
92-24 = 68 68-24 = 44 44-24 = 20 24-20 = 4 20-4 = 16
16-4 = 12 12-4 = 8 8-4 = 4
所以440 与556的最大公约数4.
19、解 这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下图所示
20、解 我们用c(单位:元)表示通话费,t(单位:分钟)表示通话时间,
则依题意有
算法步骤如下:第一步,输入通话时间t;第二步,如果t≤3,那么c = 0.2 ;否则令 c = 0.2+0.1 (t-3);
第三步,输出通话费用c ;
程序框图如图所示
21.解 (I)该算法使用了当型循环结构,因为是求30个数的和,故循环体应执行30次,其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为.算法 中的变量p实质是表示参与求和的各个数,由于它也是变化的,且满足第i个数比其前一个数大,,第个数比其前一个数大i,故应有.故(1)处应填;(2)处应填
(II)根据以上框图,可设计程序如下:
22、由于共有12位评委,所以每位选手会有12个分数,我们可以用循环语句来完成这12个分数的输入,同时设计累加变量求出这12个分数的和,本问题的关键在于从这12个输入分数中找出最大数与最小数,以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间,去我们可以先假设其中的最大数为0,最小数为10,然后每次输入一个评委的分数,就进行一次比较,若输入的数大于0,就将之代替最大数,若输入的数小于10,就用它代替最小数,依次下去,就能找出这12个数中的最大数与最小数,循环结束后,从总和中减去最大数与最小数,再除以10,就得到该选手最后的平均数.
程序框图如图所示.
