算法语言试题2[上学期]
图片预览

文档简介
高二数学单元测验题
《算法语言》
一、选择题
1.我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组解,二分法求函数零点等.对算法的描述有①对一类问题都有效;②对个别问题有效;③计算可以一步步地进行,每一步都有惟一的结果;④是一种通法,只要按部就班地做,总能得到结果.以上正确描述算法的有 ( )
A.1个 B.2个 C.3个 D.4个
2.算法的过程称为“数学机械化”,数学机械化的最大优点是可以让计算机来完成,中国当代数学家在这方面研究处于世界领先地位,为此而获得首届自然科学500万大奖的是( )
A.袁隆平 B.华罗庚
C.苏步青 D.吴文俊
3.算法
S1 m=a
S2 若bS3 若cS4 若dS5 输出m,则输出m表示 ( )
A.a,b,c,d中最大值
B.a,b,c,d中最小值
C.将a,b,c,d由小到大排序
D.将a,b,c,d由大到小排序
4.算法:
S1 输入n
S2 判断n是否是2,若n=2,则n满足条件,若n>2,则执行S3
s3 依次从2到n一1检验能不能整除n,若不能整除n,满足上述条件的是 ( )
A.质数 B.奇数 C.偶数 D.约数
5.右图输出的是
A.2005 B.65 C.64 D.63
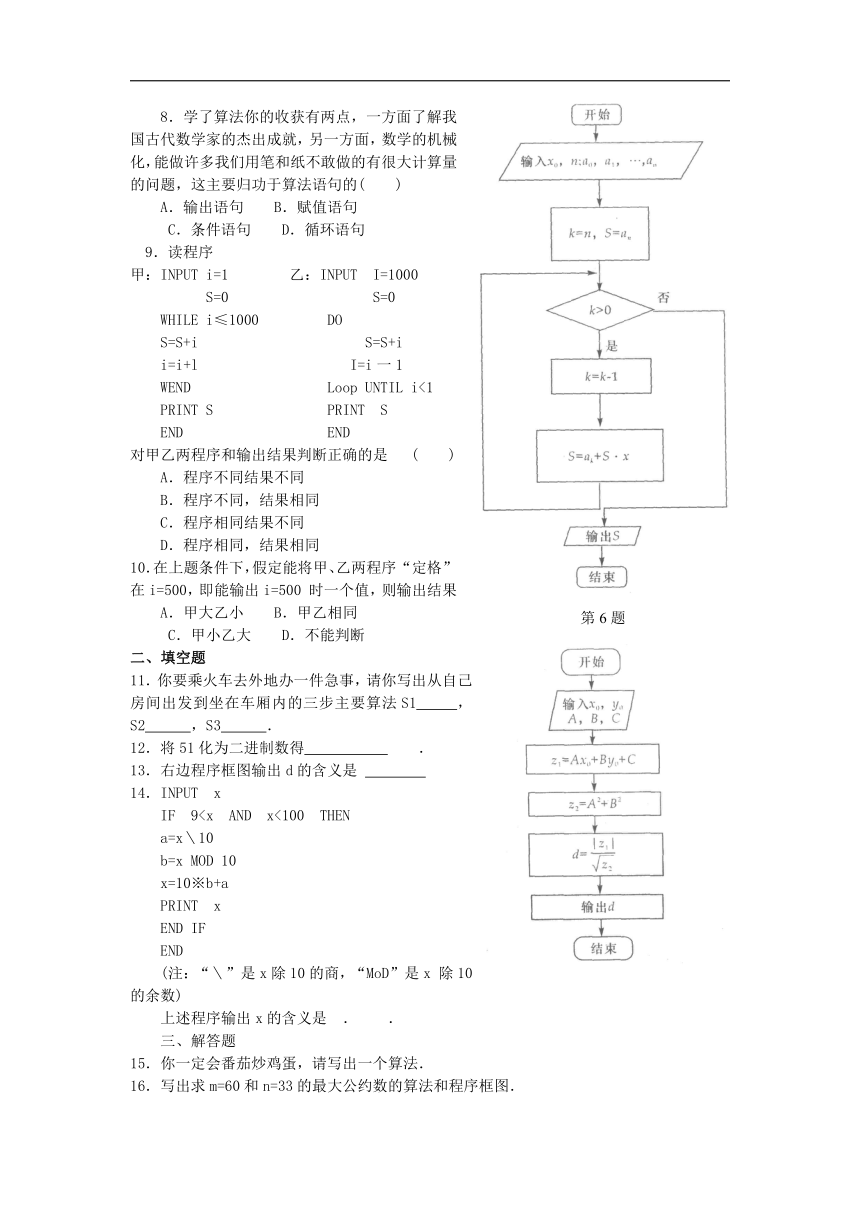
6.如下程序框图是古代一数学家的算法程序框图,它输出的结果S代表
A.一个数列的和
B.一个n次多项式系数的和
C.自变量取x。时,n次多项式函数的值
D.自变量取x。时,n个代数式的值
7.我国古代数学发展一直处于世界领先水平,特别是宋、元时期的“算法”,其中可以同欧几里德辗转相除法相媲美的是 ( )
A.割圆术 B.更相减损术 C.秦九韶算法 D.孙子乘余定理
8.学了算法你的收获有两点,一方面了解我国古代数学家的杰出成就,另一方面,数学的机械化,能做许多我们用笔和纸不敢做的有很大计算量的问题,这主要归功于算法语句的( )
A.输出语句 B.赋值语句
C.条件语句 D.循环语句
9.读程序
甲:INPUT i=1 乙:INPUT I=1000
S=0 S=0
WHILE i≤1000 DO
S=S+i S=S+i
i=i+l I=i一1
WEND Loop UNTIL i<1
PRINT S PRINT S
END END
对甲乙两程序和输出结果判断正确的是 ( )
A.程序不同结果不同
B.程序不同,结果相同
C.程序相同结果不同
D.程序相同,结果相同
10.在上题条件下,假定能将甲、乙两程序“定格”在i=500,即能输出i=500 时一个值,则输出结果
A.甲大乙小 B.甲乙相同
C.甲小乙大 D.不能判断
二、填空题
11.你要乘火车去外地办一件急事,请你写出从自己房间出发到坐在车厢内的三步主要算法S1 ,S2 ,S3 .
12.将51化为二进制数得 .
13.右边程序框图输出d的含义是
14.INPUT x
IF 9a=x\10
b=x MOD 10
x=10※b+a
PRINT x
END IF
END
(注:“\”是x除10的商,“MoD”是x 除10的余数)
上述程序输出x的含义是 . .
三、解答题
15.你一定会番茄炒鸡蛋,请写出一个算法.
16.写出求m=60和n=33的最大公约数的算法和程序框图.
17.有10个互不相等的数,写出找出其中一个最大数的算法和程序
18.假定在银行中存款10000元,按11.25%的利率,一年后连本带息将变为11125元,若将此款继续存人银行,试问多长时间就会连本带利翻一番?请用直到型和当型两种语句写出程序.
19.1982年我国大陆人口10亿3千万,编程上机计算,若人口增长率r=1%,则哪一年我国人口增长到12亿,若r=O.5%,r=O.2%又是何年?
20.给定一个年份,写出该年是不是闰年的算法,程序框图和程序.
算法语言测试题答案
一、选择题
1.C 2.D 3.B 4.A 5.D 6.C 7.B 8.D 9.B 10.C
二、填空题
11.乘车去火车站 买车票 凭票上车,
对号入座
12.110011(2)
13.点( x。,y。)到直线Ax+By+C=O的距离
14.交换十位数与个位数
三、解答题
15.【解】
S1:洗净番茄
S2:切碎番茄
S3:打好鸡蛋并调匀
S4:洗净锅,放在灶上
S5:点好煤气,打开油烟机
S6:倒人适量油,烧热
S7:倒入鸡蛋,用铲子炒匀
S8:倒入番茄,炒匀
S9:放入盐和调料,炒匀到锅中间水沸腾时,熄火
S10:盛到盘中
16.【解法一】
S1:以n 除m,得余数r=27
S2:判断r是否为零,若r=0,则n为解,若r≠0,则重复S3操作(r=27)
S3:以n作为新的m(33),以r作为新的,l(27),求新的m/n的余数r=6
S4:判断r是否为零,若r=O,则前一个n即为解,否则要继续S5操作
S5:以n 作为新的m(即m=27),以r作为新的n(即n=6),求新的余数r=3
S6:判断上一个r 是否为零,若r=O,则前一个n即为解,否则要执行S7操作
S7:以n作为新的m(m =6),r作为新的n(n=3),求新的r= O
S8:判断r是否为零,这里r=O,算法结束,得,n=3是60与33的最大公约数程序框图略
【解法二】
S1:输入60,33,将m=60,n=33
S2:求m/n余数r
S3:若r=0,则n就是所求最大公约,输出n,若r≠O,执行下一步
S4:使n 作为新的m,使r作为新的n,执行S2
程序框图(当型)
【解法三】
S1:令m=60,n=33
S2:重复执行下面序列,直到求得r=0为止
S3:求m/n的余数r
S4:令m=n,n=r
S5:输出m
(直到型)
17.【解】(一)算法
S1:输入一个数,放在MAX中
S2:i=1
S3:输入第1个数,放入x中
S4:若x>MAX,则MAX=z
S5: i=i+1
S6:若i≤9,返回S3继续执行,否则停.
(二)程序框图
18.【解】
19.【解】
r=1% 输出y=8,p=12.0681
r=O.5% 输出y=11,p=12.1329
r=O.2% 输出y=31,p=12.0222
20.【解】(一)算法
S1:输入一个年份x
S2:若z能被100整除,则执行S3否则执行 S4
S3:若x能被400整除,则x为闰年,否则x不为闰年
S4:若x能被4整除,则x为闰年,否则x不为闰年
(二)程序框图
(三)程序
《算法语言》
一、选择题
1.我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组解,二分法求函数零点等.对算法的描述有①对一类问题都有效;②对个别问题有效;③计算可以一步步地进行,每一步都有惟一的结果;④是一种通法,只要按部就班地做,总能得到结果.以上正确描述算法的有 ( )
A.1个 B.2个 C.3个 D.4个
2.算法的过程称为“数学机械化”,数学机械化的最大优点是可以让计算机来完成,中国当代数学家在这方面研究处于世界领先地位,为此而获得首届自然科学500万大奖的是( )
A.袁隆平 B.华罗庚
C.苏步青 D.吴文俊
3.算法
S1 m=a
S2 若b
A.a,b,c,d中最大值
B.a,b,c,d中最小值
C.将a,b,c,d由小到大排序
D.将a,b,c,d由大到小排序
4.算法:
S1 输入n
S2 判断n是否是2,若n=2,则n满足条件,若n>2,则执行S3
s3 依次从2到n一1检验能不能整除n,若不能整除n,满足上述条件的是 ( )
A.质数 B.奇数 C.偶数 D.约数
5.右图输出的是
A.2005 B.65 C.64 D.63
6.如下程序框图是古代一数学家的算法程序框图,它输出的结果S代表
A.一个数列的和
B.一个n次多项式系数的和
C.自变量取x。时,n次多项式函数的值
D.自变量取x。时,n个代数式的值
7.我国古代数学发展一直处于世界领先水平,特别是宋、元时期的“算法”,其中可以同欧几里德辗转相除法相媲美的是 ( )
A.割圆术 B.更相减损术 C.秦九韶算法 D.孙子乘余定理
8.学了算法你的收获有两点,一方面了解我国古代数学家的杰出成就,另一方面,数学的机械化,能做许多我们用笔和纸不敢做的有很大计算量的问题,这主要归功于算法语句的( )
A.输出语句 B.赋值语句
C.条件语句 D.循环语句
9.读程序
甲:INPUT i=1 乙:INPUT I=1000
S=0 S=0
WHILE i≤1000 DO
S=S+i S=S+i
i=i+l I=i一1
WEND Loop UNTIL i<1
PRINT S PRINT S
END END
对甲乙两程序和输出结果判断正确的是 ( )
A.程序不同结果不同
B.程序不同,结果相同
C.程序相同结果不同
D.程序相同,结果相同
10.在上题条件下,假定能将甲、乙两程序“定格”在i=500,即能输出i=500 时一个值,则输出结果
A.甲大乙小 B.甲乙相同
C.甲小乙大 D.不能判断
二、填空题
11.你要乘火车去外地办一件急事,请你写出从自己房间出发到坐在车厢内的三步主要算法S1 ,S2 ,S3 .
12.将51化为二进制数得 .
13.右边程序框图输出d的含义是
14.INPUT x
IF 9
b=x MOD 10
x=10※b+a
PRINT x
END IF
END
(注:“\”是x除10的商,“MoD”是x 除10的余数)
上述程序输出x的含义是 . .
三、解答题
15.你一定会番茄炒鸡蛋,请写出一个算法.
16.写出求m=60和n=33的最大公约数的算法和程序框图.
17.有10个互不相等的数,写出找出其中一个最大数的算法和程序
18.假定在银行中存款10000元,按11.25%的利率,一年后连本带息将变为11125元,若将此款继续存人银行,试问多长时间就会连本带利翻一番?请用直到型和当型两种语句写出程序.
19.1982年我国大陆人口10亿3千万,编程上机计算,若人口增长率r=1%,则哪一年我国人口增长到12亿,若r=O.5%,r=O.2%又是何年?
20.给定一个年份,写出该年是不是闰年的算法,程序框图和程序.
算法语言测试题答案
一、选择题
1.C 2.D 3.B 4.A 5.D 6.C 7.B 8.D 9.B 10.C
二、填空题
11.乘车去火车站 买车票 凭票上车,
对号入座
12.110011(2)
13.点( x。,y。)到直线Ax+By+C=O的距离
14.交换十位数与个位数
三、解答题
15.【解】
S1:洗净番茄
S2:切碎番茄
S3:打好鸡蛋并调匀
S4:洗净锅,放在灶上
S5:点好煤气,打开油烟机
S6:倒人适量油,烧热
S7:倒入鸡蛋,用铲子炒匀
S8:倒入番茄,炒匀
S9:放入盐和调料,炒匀到锅中间水沸腾时,熄火
S10:盛到盘中
16.【解法一】
S1:以n 除m,得余数r=27
S2:判断r是否为零,若r=0,则n为解,若r≠0,则重复S3操作(r=27)
S3:以n作为新的m(33),以r作为新的,l(27),求新的m/n的余数r=6
S4:判断r是否为零,若r=O,则前一个n即为解,否则要继续S5操作
S5:以n 作为新的m(即m=27),以r作为新的n(即n=6),求新的余数r=3
S6:判断上一个r 是否为零,若r=O,则前一个n即为解,否则要执行S7操作
S7:以n作为新的m(m =6),r作为新的n(n=3),求新的r= O
S8:判断r是否为零,这里r=O,算法结束,得,n=3是60与33的最大公约数程序框图略
【解法二】
S1:输入60,33,将m=60,n=33
S2:求m/n余数r
S3:若r=0,则n就是所求最大公约,输出n,若r≠O,执行下一步
S4:使n 作为新的m,使r作为新的n,执行S2
程序框图(当型)
【解法三】
S1:令m=60,n=33
S2:重复执行下面序列,直到求得r=0为止
S3:求m/n的余数r
S4:令m=n,n=r
S5:输出m
(直到型)
17.【解】(一)算法
S1:输入一个数,放在MAX中
S2:i=1
S3:输入第1个数,放入x中
S4:若x>MAX,则MAX=z
S5: i=i+1
S6:若i≤9,返回S3继续执行,否则停.
(二)程序框图
18.【解】
19.【解】
r=1% 输出y=8,p=12.0681
r=O.5% 输出y=11,p=12.1329
r=O.2% 输出y=31,p=12.0222
20.【解】(一)算法
S1:输入一个年份x
S2:若z能被100整除,则执行S3否则执行 S4
S3:若x能被400整除,则x为闰年,否则x不为闰年
S4:若x能被4整除,则x为闰年,否则x不为闰年
(二)程序框图
(三)程序
