算法初步第一章复习课[下学期]
图片预览






文档简介
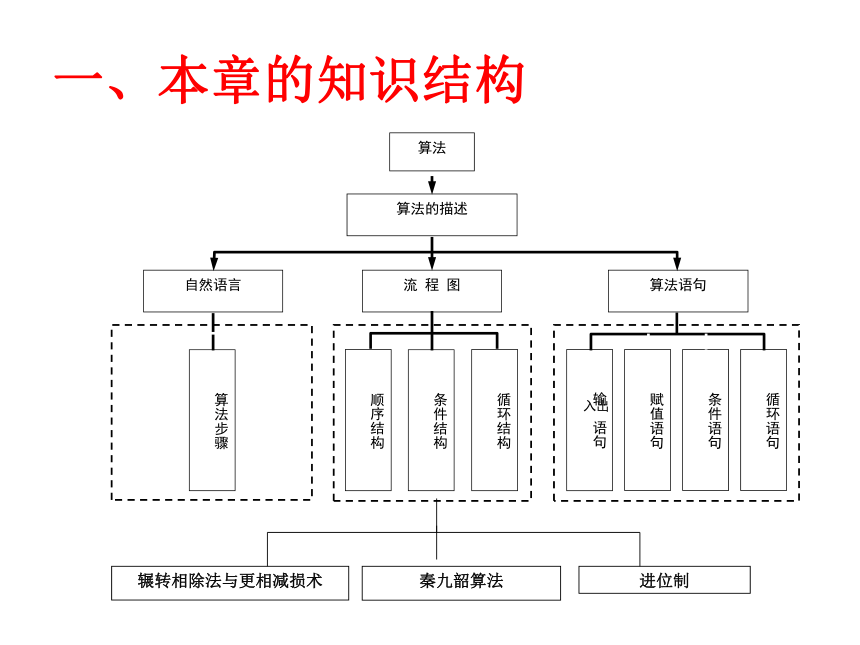
课件26张PPT。算法语言全章复习 一、本章的知识结构 辗转相除法与更相减损术秦九韶算法进位制1.四种基本的程序框
2.三种基本逻辑结构
顺序结构 、 条件结构 、循环结构
3.基本算法语句
①输入语句二.知识梳理INPUT “提示内容”;变量INPUT “提示内容1,提示内容2,提示内容3,…”;变量1,变量2,变量3,…②输出语句PRINT “提示内容”;表达式③赋值语句变量=表达式IF 条件 THEN
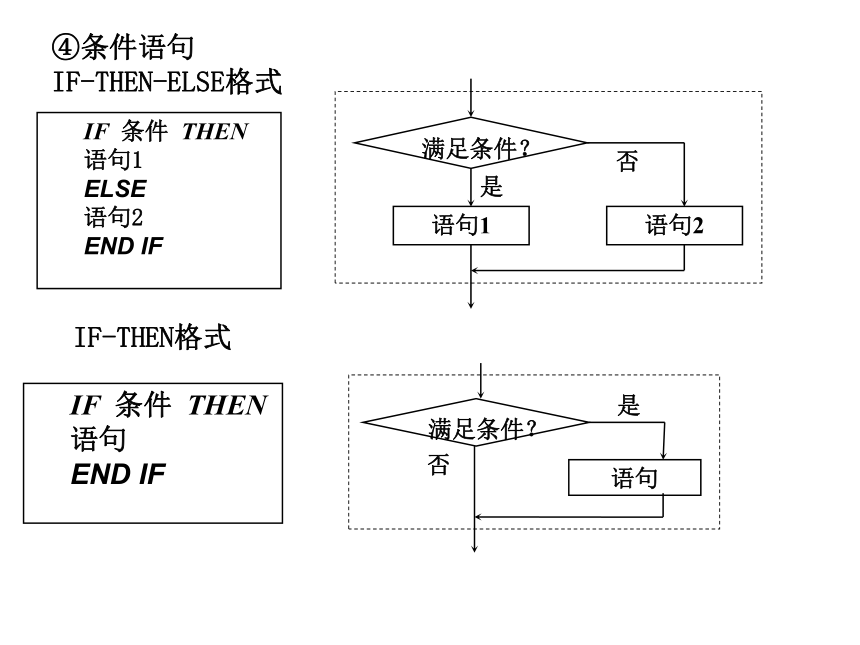
语句1
ELSE
语句2
END IF
IF 条件 THEN
语句
END IF
④条件语句
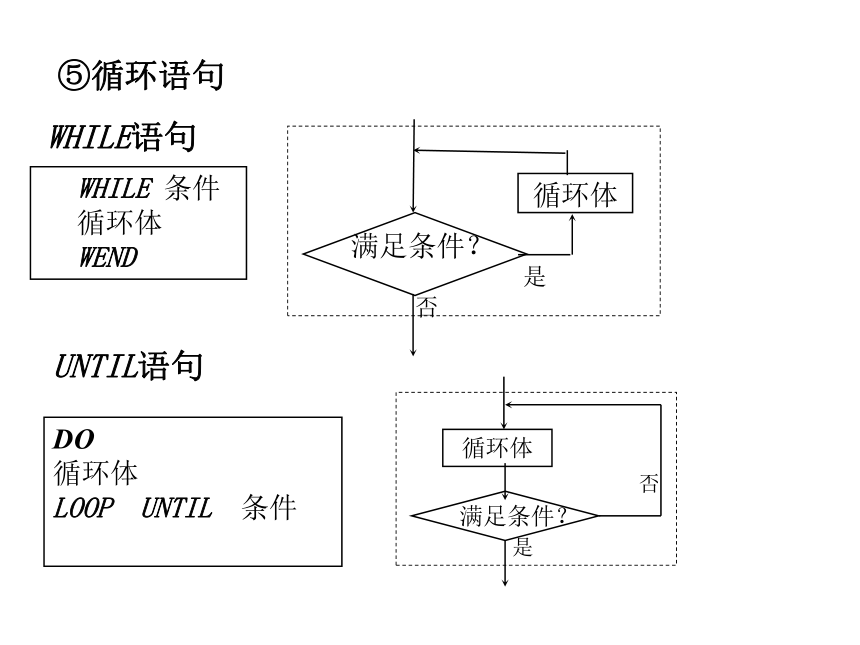
IF-THEN-ELSE格式IF-THEN格式WHILE 条件
循环体
WEND
⑤循环语句WHILE语句UNTIL语句DO
循环体
LOOP UNTIL 条件4.算法案例
案例1 辗转相除法与更相减损术
案例2 秦九韶算法
案例3 进位制考点题型1 概念的判断和理解1.下面对流程图中的图形符号的说法错误的是 ( )
A.起、止框是任何流程不可少的,表明程序开始和结束
B.输入、输出可用在算法中任何需要输入、输出的位置
C.算法中间要处理数据或计算,可分别写在不同的注释框内
D.当算法要求对两个不同的结果进行判断时,要写在判断框内三.典型例题C2.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是 ( )A.一个算法只能含有一种逻辑结构
B.一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.—个算法可以含有上述三种逻辑结构的任意组合D3.下列给出的赋值语句中正确的是 ( )A.3=A B.M=-M
C.B=A=2 D.x+y=0B考点题型2 算法、程序框图和算法语句的设计、编写 1.设计一个程序语句,输入任意三个实数,将它们按从小到大的顺序排列后输出.Input a,b,c
If a>b Then
t=a
a=b
b=t
End If
If a>c Then
t=a
a=c
c=t
End If
If b>c Then
t=b
b=c
c=t
End If
Print a,b,c
End
变式: 以下给出的是用算法基本语句描述的某一个问题的算法,根据该程序回答以下问题: (1)若输入的四个数是8,2,1,13,问输出结果是多少? (2)该程序表示的算法的功能是什么?INPUT m,n,p,q
IF m>n,m>p,m>q THEN
PRINT m
END IF
IF n>p,n>q THEN
PRINT n
END IF
IF p>q THEN
PRINT p
ELSE
PRINT q
END IF
END(1)13(2)该程序表示的算法的功能是求出任意输入的四个数m,n,p,q的最大数2:设计算法,输出1000以内整除15的所有整数,并且求它们的和。方法(一)2:设计算法,输出1000以内整除15的所有整数,并且求它们的和。方法(二)3 写一个算法程序,计算1+3+5+…+(2n-1) 的值(要求可以输入任意大于1的正奇数)INPUT “2n-1=”;2n-1
i=1
s=0
WHILE i<=2n-1
s=s+i
i=i+2
WEND
PRINT s
END思考:在上述程序语句中我们使用了WHILE格式的循环语句,能不能使用UNTIL循环? 考点题型3 由程序框图、算法语句计算算法结果 1.下列程序是求一个函数函数值的程序,在键盘上输入一个自变量x的值,输出它的函数值,若执行的结果为3,则输入的x值为?
函数的解析式是? 程序:
Input x
If x≤0 Then
y=x
Else
If x>0 And x≤l Then
y=0
Else
y=x-1
End If
End If
Print y
End2.下列程序的运行结果是( )
i=1
Sum=0
Do
Sum=sum+ 1/i
i=i+1
Loop Until i>5
Print sum
EndA. 137/60 B. 3 C. 130/60 D.1/60A3、下列各式中的S值,能设计出算法求解的是:
①s=1+2+3+…+100
②s=1+2+3+…+100+…
③s=1+2+3+…+n(n≥1,且n∈N)
A ①② B ①③ C ②③ D ①②③ 4.写出表示下列程序运算功能的算术表达式(不计算,只写式子)
n=2
T=1
While n≤5
T=n * T
n=n+1
Wend
Print T
End
表达式为? T=1×2×3×4×55. 读框图读程序630i <11 n=0
s=0
While s<=10
n=n+1
s=s+1/n
Wend
Print n
end12367考点题型4算法结果和方法的应用1. 把十进制数53转化为二进制数.变式:将二进制数101101101(2)转为八进制数101101101(2) =555(8)2. 利用辗转相除法求3869与6497的最大公约数。 解:6497=3869×1+2628
3869=2628×1+1241
2628=1241×2+146
1241=146×8+73
146=73×2+0
所以3869与6497的最大公约数为73思考:上述计算方法能否设计为程序框图?INPUT m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END变式:用更相减损术求72,120,168的最大公约数?24回顾反思 算法思想作为数学的一种基本思想,就是探求解决问题的一般性方法,并将解决问题的步骤用具体化、程序化的语言加以表述,主要作用是使计算机能代替人完成某些工作,这也是学习算法的重要原因之一.算法思想在解决某些问题时,只要能设计出一系列可操作或可计算的有限而明确的步骤,就可以通过实施这些步骤来解决问题. 1.算法的问题根本上是一个思维的问题。我们只有在掌握了一定的数学理论知识及方法的基础上,再结合算法语言的基本规则,才能设计出好的可执行的运算程序。
2.算法设计并不是一次就能成功的。我们应先有一个基本的框架,其中含有最典型最重要或最核心的算法语句或结构。然后再来思考其中的每一步的执行情况,增添一些细节,逐步完善流程图与程序。
2.三种基本逻辑结构
顺序结构 、 条件结构 、循环结构
3.基本算法语句
①输入语句二.知识梳理INPUT “提示内容”;变量INPUT “提示内容1,提示内容2,提示内容3,…”;变量1,变量2,变量3,…②输出语句PRINT “提示内容”;表达式③赋值语句变量=表达式IF 条件 THEN
语句1
ELSE
语句2
END IF
IF 条件 THEN
语句
END IF
④条件语句
IF-THEN-ELSE格式IF-THEN格式WHILE 条件
循环体
WEND
⑤循环语句WHILE语句UNTIL语句DO
循环体
LOOP UNTIL 条件4.算法案例
案例1 辗转相除法与更相减损术
案例2 秦九韶算法
案例3 进位制考点题型1 概念的判断和理解1.下面对流程图中的图形符号的说法错误的是 ( )
A.起、止框是任何流程不可少的,表明程序开始和结束
B.输入、输出可用在算法中任何需要输入、输出的位置
C.算法中间要处理数据或计算,可分别写在不同的注释框内
D.当算法要求对两个不同的结果进行判断时,要写在判断框内三.典型例题C2.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是 ( )A.一个算法只能含有一种逻辑结构
B.一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.—个算法可以含有上述三种逻辑结构的任意组合D3.下列给出的赋值语句中正确的是 ( )A.3=A B.M=-M
C.B=A=2 D.x+y=0B考点题型2 算法、程序框图和算法语句的设计、编写 1.设计一个程序语句,输入任意三个实数,将它们按从小到大的顺序排列后输出.Input a,b,c
If a>b Then
t=a
a=b
b=t
End If
If a>c Then
t=a
a=c
c=t
End If
If b>c Then
t=b
b=c
c=t
End If
Print a,b,c
End
变式: 以下给出的是用算法基本语句描述的某一个问题的算法,根据该程序回答以下问题: (1)若输入的四个数是8,2,1,13,问输出结果是多少? (2)该程序表示的算法的功能是什么?INPUT m,n,p,q
IF m>n,m>p,m>q THEN
PRINT m
END IF
IF n>p,n>q THEN
PRINT n
END IF
IF p>q THEN
PRINT p
ELSE
PRINT q
END IF
END(1)13(2)该程序表示的算法的功能是求出任意输入的四个数m,n,p,q的最大数2:设计算法,输出1000以内整除15的所有整数,并且求它们的和。方法(一)2:设计算法,输出1000以内整除15的所有整数,并且求它们的和。方法(二)3 写一个算法程序,计算1+3+5+…+(2n-1) 的值(要求可以输入任意大于1的正奇数)INPUT “2n-1=”;2n-1
i=1
s=0
WHILE i<=2n-1
s=s+i
i=i+2
WEND
PRINT s
END思考:在上述程序语句中我们使用了WHILE格式的循环语句,能不能使用UNTIL循环? 考点题型3 由程序框图、算法语句计算算法结果 1.下列程序是求一个函数函数值的程序,在键盘上输入一个自变量x的值,输出它的函数值,若执行的结果为3,则输入的x值为?
函数的解析式是? 程序:
Input x
If x≤0 Then
y=x
Else
If x>0 And x≤l Then
y=0
Else
y=x-1
End If
End If
Print y
End2.下列程序的运行结果是( )
i=1
Sum=0
Do
Sum=sum+ 1/i
i=i+1
Loop Until i>5
Print sum
EndA. 137/60 B. 3 C. 130/60 D.1/60A3、下列各式中的S值,能设计出算法求解的是:
①s=1+2+3+…+100
②s=1+2+3+…+100+…
③s=1+2+3+…+n(n≥1,且n∈N)
A ①② B ①③ C ②③ D ①②③ 4.写出表示下列程序运算功能的算术表达式(不计算,只写式子)
n=2
T=1
While n≤5
T=n * T
n=n+1
Wend
Print T
End
表达式为? T=1×2×3×4×55. 读框图读程序630i <11 n=0
s=0
While s<=10
n=n+1
s=s+1/n
Wend
Print n
end12367考点题型4算法结果和方法的应用1. 把十进制数53转化为二进制数.变式:将二进制数101101101(2)转为八进制数101101101(2) =555(8)2. 利用辗转相除法求3869与6497的最大公约数。 解:6497=3869×1+2628
3869=2628×1+1241
2628=1241×2+146
1241=146×8+73
146=73×2+0
所以3869与6497的最大公约数为73思考:上述计算方法能否设计为程序框图?INPUT m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END变式:用更相减损术求72,120,168的最大公约数?24回顾反思 算法思想作为数学的一种基本思想,就是探求解决问题的一般性方法,并将解决问题的步骤用具体化、程序化的语言加以表述,主要作用是使计算机能代替人完成某些工作,这也是学习算法的重要原因之一.算法思想在解决某些问题时,只要能设计出一系列可操作或可计算的有限而明确的步骤,就可以通过实施这些步骤来解决问题. 1.算法的问题根本上是一个思维的问题。我们只有在掌握了一定的数学理论知识及方法的基础上,再结合算法语言的基本规则,才能设计出好的可执行的运算程序。
2.算法设计并不是一次就能成功的。我们应先有一个基本的框架,其中含有最典型最重要或最核心的算法语句或结构。然后再来思考其中的每一步的执行情况,增添一些细节,逐步完善流程图与程序。
