第一章算法练习课[下学期]
图片预览









文档简介
课件32张PPT。算法初步练习课1.下面的结论正确的是 ( )
A、一个程序的算法步骤是可逆的
B、一个算法可以无止境地运算下去的
C、完成一件事情的算法有且只有一种
D、设计算法要本着简单方便的原则 2、早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法 ( )
A、S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播B、S1刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播C、S1刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播 D、S1吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶 D C 小结:算法的基本特点1、有穷性: 一个算法应包括有限的操作步骤,能在执行有穷的操作步骤之后结束。2、确定性: 算法的计算规则及相应的计算步骤必须是唯一确定的,既不能含糊其词,也不能有二义性。3、可行性: 算法中的每一个步骤都是可以在有限的时间内完成的基本操作,并能得到确定的结果 。3.算法S1 m=a
S2 若bS3 若cS4 若dS5 输出m,则输出m表示 ( )
A.a,b,c,d中最大值
B.a,b,c,d中最小值
C.将a,b,c,d由小到大排序
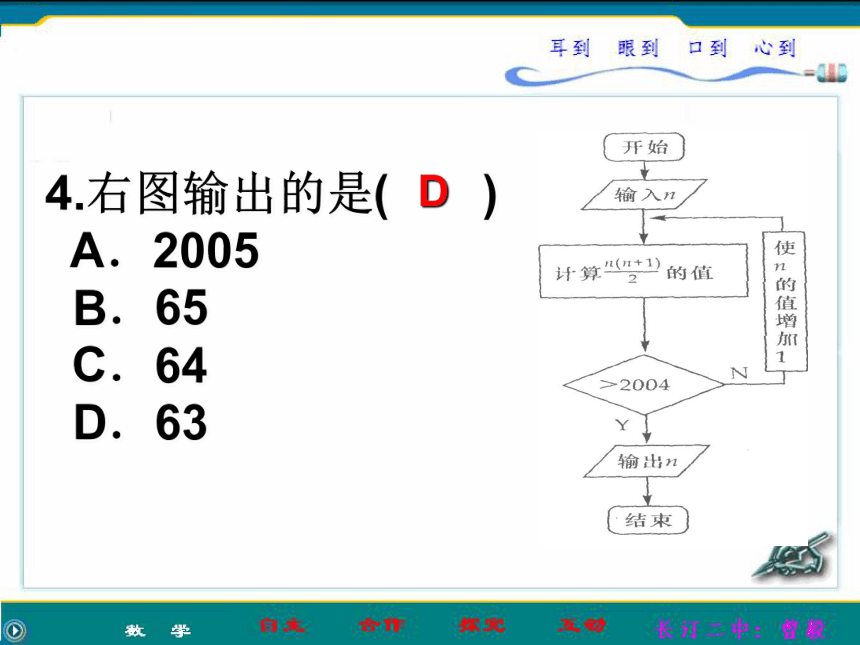
D.将a,b,c,d由大到小排序B 4.右图输出的是( )
A.2005
B.65
C.64
D.63D 5、下列给出的赋值语句中正确的是( )
5 = M B. x =-x
C. B=A=3 D. x +y = 0
6、下列选项那个是正确的( )
A、INPUT A; B B. INPUT B=3
C. PRINT y=2*x+1 D. PRINT 4*x
B D 算法基本语句的格式:INPUT “提示文字”;变量PRINT “提示内容”;变量变量=表达式可对程序中的变量赋值可输出表达式的值,计算可对程序中的变量赋值,计算INPUT语句不但可以给单个变量赋值,还可以给多个变量赋值。其中“提示内容”可省略。如:可写成“INPUT a”;但不能写成“INPUT a+b”或“INPUT 3”。(1)如果某一个变量已经被赋值,则可以用PRINT语句打印出来该变量的值。(2)用一个PRINT语句可以打印出若干个变量的值。 (3)用PRINT语句可以输出表达式的值。赋值语句将表达式代表的值赋给变量. “=”叫做赋值号.计算机执行赋值语句时,先计算 “=”右边表达式的值,然后把这个值赋给 “=”左边的变量.二、条件语句 算法中的条件结构由条件语句来表达。条件语句的一般格式:(IF-THEN-ELSE格式)IF 条件 THEN
语句1
ELSE
语句2
END IF
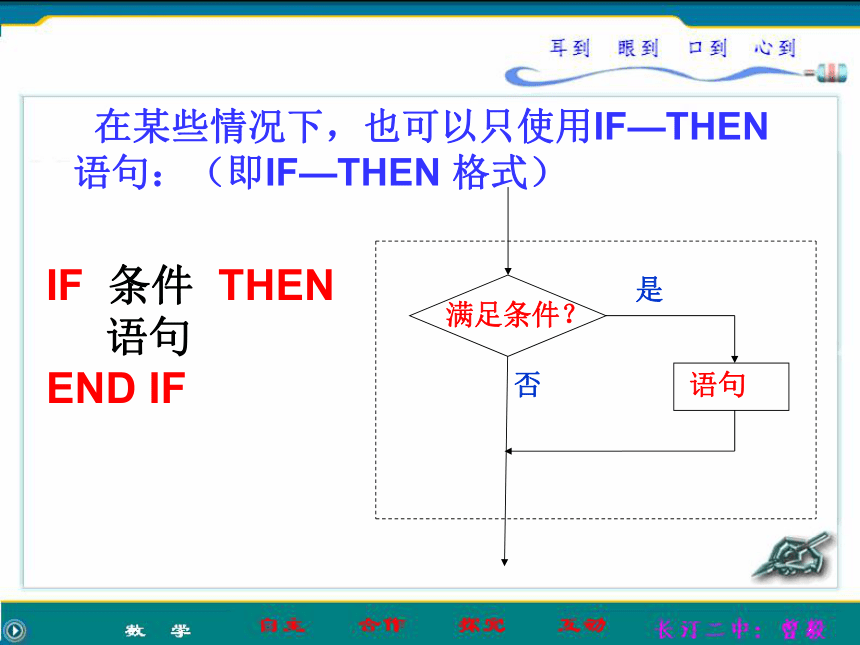
在某些情况下,也可以只使用IF—THEN语句:(即IF—THEN 格式)IF 条件 THEN
语句
END IF
3、循环语句:WHILE 条件
循环体
WEND(1)WHILE语句的一般格式: 当计算机遇到WHILE语句时,先判断条件的真假,如
果条件符合,就执行WHILE与WEND之间的循环体;然
后再检查上述条件,如果条件仍符合,再次执行循环体,
这个过程反复进行,直到某一次条件不符合为止.这时,
计算机将不执行循环体,直接跳到WEND语句后,接着执
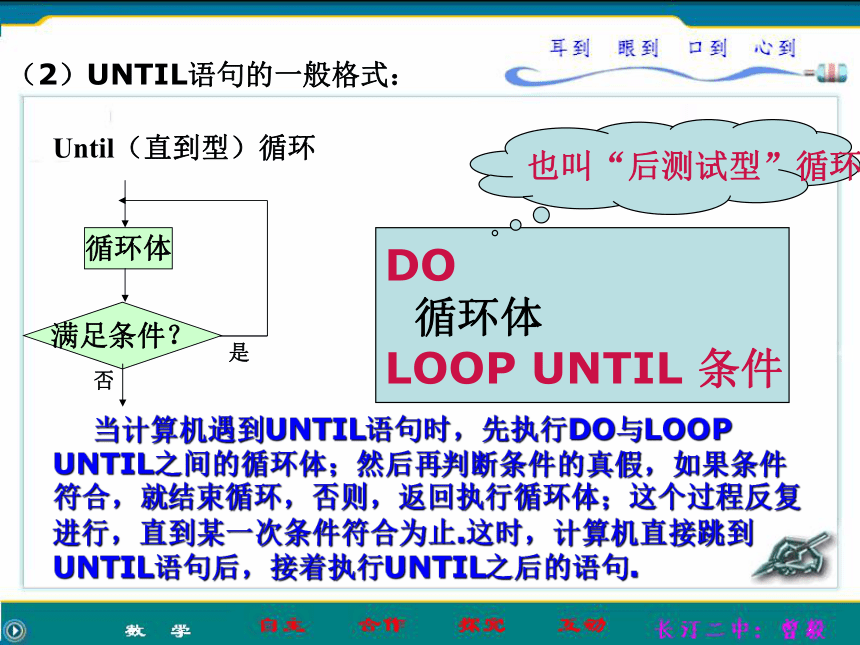
行WEND之后的语句.Until(直到型)循环DO
循环体
LOOP UNTIL 条件(2)UNTIL语句的一般格式: 当计算机遇到UNTIL语句时,先执行DO与LOOP UNTIL之间的循环体;然后再判断条件的真假,如果条件符合,就结束循环,否则,返回执行循环体;这个过程反复进行,直到某一次条件符合为止.这时,计算机直接跳到UNTIL语句后,接着执行UNTIL之后的语句.i=11
s=1
DO
s= s * i
i = i-1
LOOP UNTIL “条件”
PRINT s
END
(第8题)
7、如果右边程序执行后输出的结果是990,那么
在程序until后面的“条件”应为( )
A.i > 10 B. i <8 C. i <=9 D.i<9D 8.读程序
甲: i=1 乙: i=1000
S=0 S=0
WHILE i<=1000 DO
S=S+i S=S+i
i=i+l i=i-1
WEND LOOP UNTIL i<1
PRINT S PRINT S
END END
对甲乙两程序和输出结果判断正确的是 ( )
A.程序不同结果不同 B.程序不同,结果相同
C.程序相同结果不同 D.程序相同,结果相同B 9.在上题条件下,假定能将甲、乙两程序“定格”在i=500,即能输出i=500 时一个值,则输出结果 ( )
A.甲大乙小 B.甲乙相同
C.甲小乙大 D.不能判断C 10、有如下程序框图(如右图所示),则该程序框图表示的算法的功能是________ 答案:计算并输出使1×3×5×7…× >10 000
成立的最小整数. 11、上面是求解一元二次方程的流程图,根据题意填写:
(1) ;
(2) ;(3) 。 ? <0 输出x1,x2 12、以下给出的各数中不可能是八进制数的是( )
A.123 B.10 110
C.4724 D.7 857D 13.将二进制数1010 101(2) 化为十进制结果为 ;
再将该数化为八进制数,结果为 . 14.计算11011(2)-101(2)
= (用二进制表示) 85 125(8) 10110(2) 15. 已知算法: ① 将该算法用流程图描述之;
② 写出该程序。
S1、 输入 X
S2 、 若X<1,执行 S3. 否则执行S6
S3 、 Y =X- 2
S4、输出 Y
S5、 结束
S6、 若X=1 ,执行S7;否则执行S10;
S7 Y =0
S8 输出Y
S9 结束
S10 Y= 2X+1
S11 输出Y
S12 结束 是是否否INPUT X
IF X<1 THEN
Y=X-2
ELSE
IF X=1 THEN
Y=O
ELSE
Y=2X+1
END IF
END IF
PRINT Y
END程序框图:程序:小结:1、画程序框图 的方法: 算法的设计是画程序框图的基础,我们通过对问题的分析,写出相应的算法步骤,画程序框图之前应先对算法问题设计的合理性进行探讨,然后分析算法的逻辑结构和各步骤(输入、输出、判断、赋值和计算)的功能,画出相应的程序框图.如果设计的程序框图较为复杂,就要采取“逐步求精”的思想设计框图,先将问题中的简单部分明确出来,再逐步对复杂部分进行细化,然后一步一步向前推进,从而设计出程序框图.
小结:2、程序设计的方法: 算法设计和程序框图是程序设计的基础,我们根据算法的三种逻辑结构,对应五种不同功能的基本算法语句,同时兼顾基本语句的格式要求从而完成程序设计,在程序设计中特别值得注意的是条件语句中条件的表达和循环语句中有关循环变量的取值范围.
程序设计的基本方法是“自上而下、逐步求精”,这种方法与写文章采用的方法类似,即首先把一个复杂的大问题分解成若干相对独立的小问题.若小问题仍较为复杂,则可以把小问题分解成若干子问题,这种不断地分解,使得小问题或子问题简单到能够直接用程序的三种基本结构乃至是五种基本语句表达清楚为止.然后对应每一个小问题或子问题编写出一个功能上相对独立的程序块(模块)来,最后把每个模块统一组装,完成程序.16、设计算法求的值,写出用基本语句编写的程序. 解 这是一个累加求和问题,共49项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如右图所示 程序如下: INPUT“S,i=”;S,i DO S=S+1/i*(i+1) i=i+1 LOOP UNTIL i>49 PRINT S END练习:请把上述程序改用当型循环结构。概念回顾基本方法
(1)编写一个程序的三个步骤:
第一步:算法分析:根据提供的问题,利用数学及相关学科的知识,设计出解决问题的算法;
第二步:画出程序框图:依据算法分析,画出对应的程序框图;
第三步:写出程序:耕具程序框图中的算法步骤,逐步把算法用相应的程序语句表达出来.概念回顾(2)何时应用条件结构?
当问题设计到一些判断,进行分类或分情况,或者比较大小时,应用条件结构;分成三种类型以上(包括三种)时,由边界开始逐一分类,应用多重条件结构.注意条件的边界值.概念回顾(3)何时应用循环结构?
当反复执行某一步骤或过程时,应用循环结构.当型循环是先判断条件,条件满足再执行循环体,不满足退出循环;直到型循环是先执行循环体,再判断条件,不满足条件时执行循环体,满足时退出循环.
应用循环结构前:①确定循环变量和初始条件;②确定算法中反复执行的部分,即循环体;③确定循环的终止条件.17.用辗转相除法求210与162的最大公约数,
并用更相减损术检验。解:用辗转相除法:
210=162×1+48162=48×3+1848=18×2+12∴210与162的最大公约数是6。18=12×1+612=6×2+0用更相减损术求得:210与162均为偶数,故可化为105与81105-81=2481-24=5757-24=3333-24=924-9=1515-9=69-6=36-3=3而3×2=6故以上求得得结果是正确的。105与81的最大公约数是318、《中华人民共和国个人所得税法》规定,公民月工资,薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税 所得额,此项税款按下表分段累进计算:试写出工资x (x5000 元)与税收 y的函数关系式,并写出计算应纳税所得额的的程序。解:y= INPUT X IF X<=800 THEN Y=0 ELSE IF X<=1300 THEN Y=(X-800)*0.05 ELSE IF X<=2800 THEN Y=25+(X-1300)*0.1 ELSE IF X<=5800 THEN Y=175+(X-2800)*0.15 END IF END IF END IF END IF PRINT Y END程序:19、给出30个数:1,2,4,7,……,
其规律是:第1个数是1,第2个数比第1
个数大1, 第3个数比第2个数大2,第4个
数比第3个数大3,依此类推.要计算这30
个数的和,现已给出了该问题算法的程
序框图(如图所示),
(I)请在图中判断框内(1)处和执行框中
的(2)处填上合适的语句,使之能完成该
题算法功能;
(II)根据程序框图写出程序.i=1
p=1
s=0
WHILE i<=30
s=s+p
p=p+i
i=i+1
WEND
PRINT a
END程序是:学而不思则惘,思而不学则怠温馨提示:
A、一个程序的算法步骤是可逆的
B、一个算法可以无止境地运算下去的
C、完成一件事情的算法有且只有一种
D、设计算法要本着简单方便的原则 2、早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法 ( )
A、S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播B、S1刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播C、S1刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播 D、S1吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶 D C 小结:算法的基本特点1、有穷性: 一个算法应包括有限的操作步骤,能在执行有穷的操作步骤之后结束。2、确定性: 算法的计算规则及相应的计算步骤必须是唯一确定的,既不能含糊其词,也不能有二义性。3、可行性: 算法中的每一个步骤都是可以在有限的时间内完成的基本操作,并能得到确定的结果 。3.算法S1 m=a
S2 若b
A.a,b,c,d中最大值
B.a,b,c,d中最小值
C.将a,b,c,d由小到大排序
D.将a,b,c,d由大到小排序B 4.右图输出的是( )
A.2005
B.65
C.64
D.63D 5、下列给出的赋值语句中正确的是( )
5 = M B. x =-x
C. B=A=3 D. x +y = 0
6、下列选项那个是正确的( )
A、INPUT A; B B. INPUT B=3
C. PRINT y=2*x+1 D. PRINT 4*x
B D 算法基本语句的格式:INPUT “提示文字”;变量PRINT “提示内容”;变量变量=表达式可对程序中的变量赋值可输出表达式的值,计算可对程序中的变量赋值,计算INPUT语句不但可以给单个变量赋值,还可以给多个变量赋值。其中“提示内容”可省略。如:可写成“INPUT a”;但不能写成“INPUT a+b”或“INPUT 3”。(1)如果某一个变量已经被赋值,则可以用PRINT语句打印出来该变量的值。(2)用一个PRINT语句可以打印出若干个变量的值。 (3)用PRINT语句可以输出表达式的值。赋值语句将表达式代表的值赋给变量. “=”叫做赋值号.计算机执行赋值语句时,先计算 “=”右边表达式的值,然后把这个值赋给 “=”左边的变量.二、条件语句 算法中的条件结构由条件语句来表达。条件语句的一般格式:(IF-THEN-ELSE格式)IF 条件 THEN
语句1
ELSE
语句2
END IF
在某些情况下,也可以只使用IF—THEN语句:(即IF—THEN 格式)IF 条件 THEN
语句
END IF
3、循环语句:WHILE 条件
循环体
WEND(1)WHILE语句的一般格式: 当计算机遇到WHILE语句时,先判断条件的真假,如
果条件符合,就执行WHILE与WEND之间的循环体;然
后再检查上述条件,如果条件仍符合,再次执行循环体,
这个过程反复进行,直到某一次条件不符合为止.这时,
计算机将不执行循环体,直接跳到WEND语句后,接着执
行WEND之后的语句.Until(直到型)循环DO
循环体
LOOP UNTIL 条件(2)UNTIL语句的一般格式: 当计算机遇到UNTIL语句时,先执行DO与LOOP UNTIL之间的循环体;然后再判断条件的真假,如果条件符合,就结束循环,否则,返回执行循环体;这个过程反复进行,直到某一次条件符合为止.这时,计算机直接跳到UNTIL语句后,接着执行UNTIL之后的语句.i=11
s=1
DO
s= s * i
i = i-1
LOOP UNTIL “条件”
PRINT s
END
(第8题)
7、如果右边程序执行后输出的结果是990,那么
在程序until后面的“条件”应为( )
A.i > 10 B. i <8 C. i <=9 D.i<9D 8.读程序
甲: i=1 乙: i=1000
S=0 S=0
WHILE i<=1000 DO
S=S+i S=S+i
i=i+l i=i-1
WEND LOOP UNTIL i<1
PRINT S PRINT S
END END
对甲乙两程序和输出结果判断正确的是 ( )
A.程序不同结果不同 B.程序不同,结果相同
C.程序相同结果不同 D.程序相同,结果相同B 9.在上题条件下,假定能将甲、乙两程序“定格”在i=500,即能输出i=500 时一个值,则输出结果 ( )
A.甲大乙小 B.甲乙相同
C.甲小乙大 D.不能判断C 10、有如下程序框图(如右图所示),则该程序框图表示的算法的功能是________ 答案:计算并输出使1×3×5×7…× >10 000
成立的最小整数. 11、上面是求解一元二次方程的流程图,根据题意填写:
(1) ;
(2) ;(3) 。 ? <0 输出x1,x2 12、以下给出的各数中不可能是八进制数的是( )
A.123 B.10 110
C.4724 D.7 857D 13.将二进制数1010 101(2) 化为十进制结果为 ;
再将该数化为八进制数,结果为 . 14.计算11011(2)-101(2)
= (用二进制表示) 85 125(8) 10110(2) 15. 已知算法: ① 将该算法用流程图描述之;
② 写出该程序。
S1、 输入 X
S2 、 若X<1,执行 S3. 否则执行S6
S3 、 Y =X- 2
S4、输出 Y
S5、 结束
S6、 若X=1 ,执行S7;否则执行S10;
S7 Y =0
S8 输出Y
S9 结束
S10 Y= 2X+1
S11 输出Y
S12 结束 是是否否INPUT X
IF X<1 THEN
Y=X-2
ELSE
IF X=1 THEN
Y=O
ELSE
Y=2X+1
END IF
END IF
PRINT Y
END程序框图:程序:小结:1、画程序框图 的方法: 算法的设计是画程序框图的基础,我们通过对问题的分析,写出相应的算法步骤,画程序框图之前应先对算法问题设计的合理性进行探讨,然后分析算法的逻辑结构和各步骤(输入、输出、判断、赋值和计算)的功能,画出相应的程序框图.如果设计的程序框图较为复杂,就要采取“逐步求精”的思想设计框图,先将问题中的简单部分明确出来,再逐步对复杂部分进行细化,然后一步一步向前推进,从而设计出程序框图.
小结:2、程序设计的方法: 算法设计和程序框图是程序设计的基础,我们根据算法的三种逻辑结构,对应五种不同功能的基本算法语句,同时兼顾基本语句的格式要求从而完成程序设计,在程序设计中特别值得注意的是条件语句中条件的表达和循环语句中有关循环变量的取值范围.
程序设计的基本方法是“自上而下、逐步求精”,这种方法与写文章采用的方法类似,即首先把一个复杂的大问题分解成若干相对独立的小问题.若小问题仍较为复杂,则可以把小问题分解成若干子问题,这种不断地分解,使得小问题或子问题简单到能够直接用程序的三种基本结构乃至是五种基本语句表达清楚为止.然后对应每一个小问题或子问题编写出一个功能上相对独立的程序块(模块)来,最后把每个模块统一组装,完成程序.16、设计算法求的值,写出用基本语句编写的程序. 解 这是一个累加求和问题,共49项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如右图所示 程序如下: INPUT“S,i=”;S,i DO S=S+1/i*(i+1) i=i+1 LOOP UNTIL i>49 PRINT S END练习:请把上述程序改用当型循环结构。概念回顾基本方法
(1)编写一个程序的三个步骤:
第一步:算法分析:根据提供的问题,利用数学及相关学科的知识,设计出解决问题的算法;
第二步:画出程序框图:依据算法分析,画出对应的程序框图;
第三步:写出程序:耕具程序框图中的算法步骤,逐步把算法用相应的程序语句表达出来.概念回顾(2)何时应用条件结构?
当问题设计到一些判断,进行分类或分情况,或者比较大小时,应用条件结构;分成三种类型以上(包括三种)时,由边界开始逐一分类,应用多重条件结构.注意条件的边界值.概念回顾(3)何时应用循环结构?
当反复执行某一步骤或过程时,应用循环结构.当型循环是先判断条件,条件满足再执行循环体,不满足退出循环;直到型循环是先执行循环体,再判断条件,不满足条件时执行循环体,满足时退出循环.
应用循环结构前:①确定循环变量和初始条件;②确定算法中反复执行的部分,即循环体;③确定循环的终止条件.17.用辗转相除法求210与162的最大公约数,
并用更相减损术检验。解:用辗转相除法:
210=162×1+48162=48×3+1848=18×2+12∴210与162的最大公约数是6。18=12×1+612=6×2+0用更相减损术求得:210与162均为偶数,故可化为105与81105-81=2481-24=5757-24=3333-24=924-9=1515-9=69-6=36-3=3而3×2=6故以上求得得结果是正确的。105与81的最大公约数是318、《中华人民共和国个人所得税法》规定,公民月工资,薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税 所得额,此项税款按下表分段累进计算:试写出工资x (x5000 元)与税收 y的函数关系式,并写出计算应纳税所得额的的程序。解:y= INPUT X IF X<=800 THEN Y=0 ELSE IF X<=1300 THEN Y=(X-800)*0.05 ELSE IF X<=2800 THEN Y=25+(X-1300)*0.1 ELSE IF X<=5800 THEN Y=175+(X-2800)*0.15 END IF END IF END IF END IF PRINT Y END程序:19、给出30个数:1,2,4,7,……,
其规律是:第1个数是1,第2个数比第1
个数大1, 第3个数比第2个数大2,第4个
数比第3个数大3,依此类推.要计算这30
个数的和,现已给出了该问题算法的程
序框图(如图所示),
(I)请在图中判断框内(1)处和执行框中
的(2)处填上合适的语句,使之能完成该
题算法功能;
(II)根据程序框图写出程序.i=1
p=1
s=0
WHILE i<=30
s=s+p
p=p+i
i=i+1
WEND
PRINT a
END程序是:学而不思则惘,思而不学则怠温馨提示:
