23.1图形的旋转(一)
文档属性
| 名称 | 23.1图形的旋转(一) |  | |
| 格式 | zip | ||
| 文件大小 | 890.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-27 22:28:45 | ||
图片预览









文档简介
课件32张PPT。23.1图形的旋转(一)自转与公转
(1)上面情景中的转动现象,有什么共同的特征?
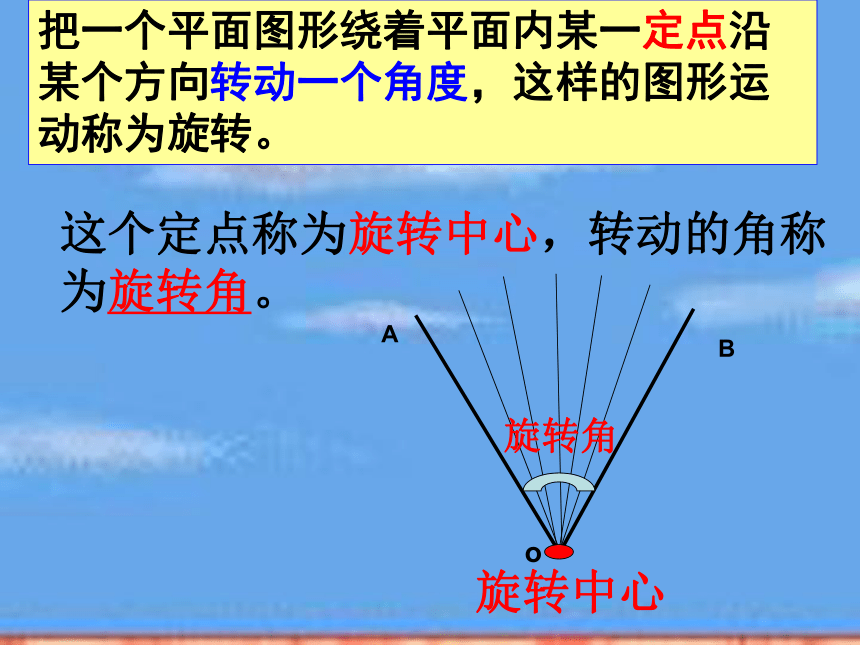
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?这个定点称为旋转中心,转动的角称为旋转角。把一个平面图形绕着平面内某一定点沿某个方向转动一个角度,这样的图形运动称为旋转。AoB归纳定义 把一个图形绕着某一定点O转动一个角度的图形变换叫做旋转.这个定点O叫旋转中心,转动的角叫做旋转角. 如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点. 动态演示OP′P 下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5 练习:平移和旋转的异同:
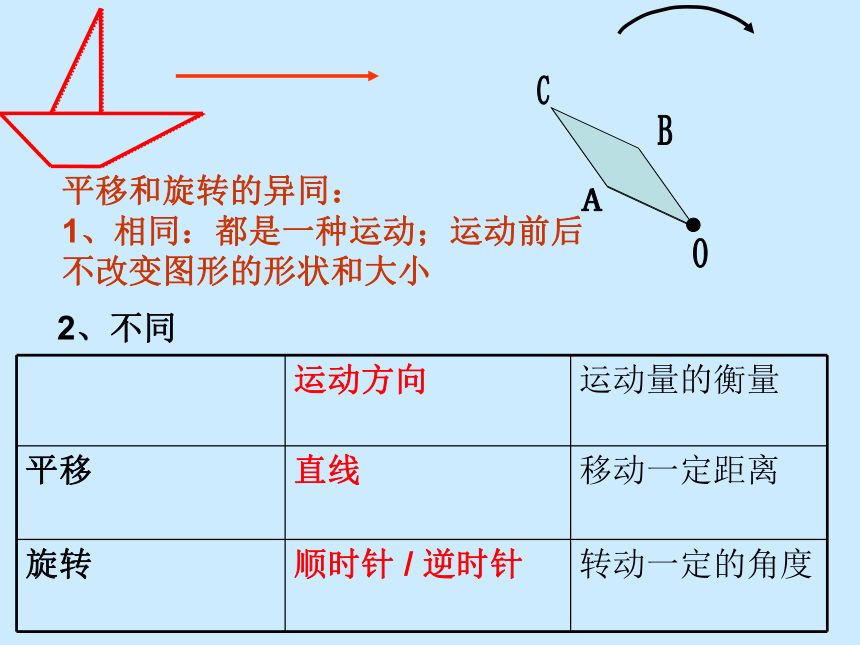
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
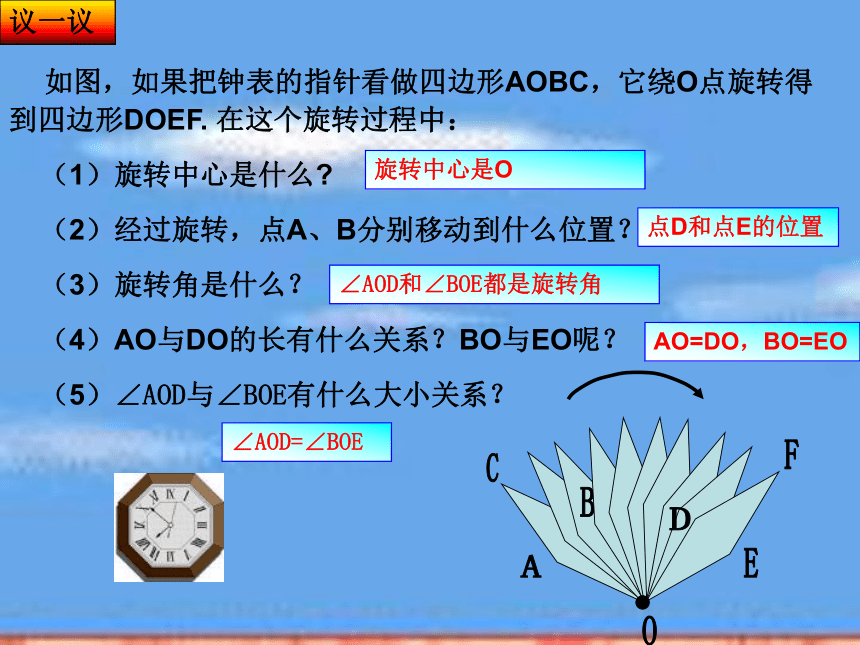
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?议一议旋转中心是O点D和点E的位置AO=DO,BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEF旋转的基本性质:1、对应点到旋转中心的距离相等;
2、对应点与旋转中心所连线段的夹角等于旋转角;
对应点于旋转中心连线所成的角彼此相等;
3、旋转前、后的图形全等。例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度? 例2 :如图,?ABC是等边三角形,D是BC上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置? 解:(1)旋转中心是A; (2)旋转了60度; (3)点M转到了AC的中点位置上.练习1、如图正方形CDEF旋转后能与正方形ABCD重合,若O是CD的中点那么图形上可以作为旋转中心的点是_________2、如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm ,∠EBF=______练习3、如图将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A’点位置,若A’C⊥AB,求∠B’A’C的度数。练习4、如图∠C=30°,△ABC绕A点逆时针旋转30°后得到△AB’C’,则图中度数是30°的角有_____个.练习旋转作图AO点的旋转作法例1 、将A点绕O点沿顺时针方向旋转60?.作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.B旋转作图AO线段的旋转作法例2 、 将线段AB绕O点沿顺时针方向旋转60?.分析:作法:
将点A绕点O顺时针旋转60?,得
点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.CBD旋转作图图形的旋转作法例3、 如图,△ABC绕C点旋转后,顶点A的对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.作法:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CF上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE将等边△ABC绕着点C按某个方向旋转900后得到△A/B/C ABCA/B/将等边△ABC绕着点o按某个方向旋转900后得到△A/B/C
ABC.A/B/C/0旋转作图练习1:将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.练习2:如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置. 设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE . 解:因为点A是旋转中心,所以它的对应点是它本身. 在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合. 因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.与旋转有关的中考题:1、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等”是否正确,若正确请说明理由,若不正确请举反例说明;
ABCDGFE2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由. 可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?练习1:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 18002次 1200 , 2400 5次 600, 1200, 1800, 2400, 3000
3个 1次 600练习2:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGHo练习3: 图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的?课堂回顾:这节课,主要学习了什么?旋转的概念旋转的性质旋转作图利用旋转设计图案
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?这个定点称为旋转中心,转动的角称为旋转角。把一个平面图形绕着平面内某一定点沿某个方向转动一个角度,这样的图形运动称为旋转。AoB归纳定义 把一个图形绕着某一定点O转动一个角度的图形变换叫做旋转.这个定点O叫旋转中心,转动的角叫做旋转角. 如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点. 动态演示OP′P 下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5 练习:平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?议一议旋转中心是O点D和点E的位置AO=DO,BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEF旋转的基本性质:1、对应点到旋转中心的距离相等;
2、对应点与旋转中心所连线段的夹角等于旋转角;
对应点于旋转中心连线所成的角彼此相等;
3、旋转前、后的图形全等。例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度? 例2 :如图,?ABC是等边三角形,D是BC上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置? 解:(1)旋转中心是A; (2)旋转了60度; (3)点M转到了AC的中点位置上.练习1、如图正方形CDEF旋转后能与正方形ABCD重合,若O是CD的中点那么图形上可以作为旋转中心的点是_________2、如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm ,∠EBF=______练习3、如图将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A’点位置,若A’C⊥AB,求∠B’A’C的度数。练习4、如图∠C=30°,△ABC绕A点逆时针旋转30°后得到△AB’C’,则图中度数是30°的角有_____个.练习旋转作图AO点的旋转作法例1 、将A点绕O点沿顺时针方向旋转60?.作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.B旋转作图AO线段的旋转作法例2 、 将线段AB绕O点沿顺时针方向旋转60?.分析:作法:
将点A绕点O顺时针旋转60?,得
点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.CBD旋转作图图形的旋转作法例3、 如图,△ABC绕C点旋转后,顶点A的对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.作法:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CF上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE将等边△ABC绕着点C按某个方向旋转900后得到△A/B/C ABCA/B/将等边△ABC绕着点o按某个方向旋转900后得到△A/B/C
ABC.A/B/C/0旋转作图练习1:将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.练习2:如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置. 设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE . 解:因为点A是旋转中心,所以它的对应点是它本身. 在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合. 因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.与旋转有关的中考题:1、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等”是否正确,若正确请说明理由,若不正确请举反例说明;
ABCDGFE2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由. 可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?练习1:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 18002次 1200 , 2400 5次 600, 1200, 1800, 2400, 3000
3个 1次 600练习2:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGHo练习3: 图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的?课堂回顾:这节课,主要学习了什么?旋转的概念旋转的性质旋转作图利用旋转设计图案
同课章节目录
