24.2.3圆与圆的位置关系课件
文档属性
| 名称 | 24.2.3圆与圆的位置关系课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-28 13:36:38 | ||
图片预览








文档简介
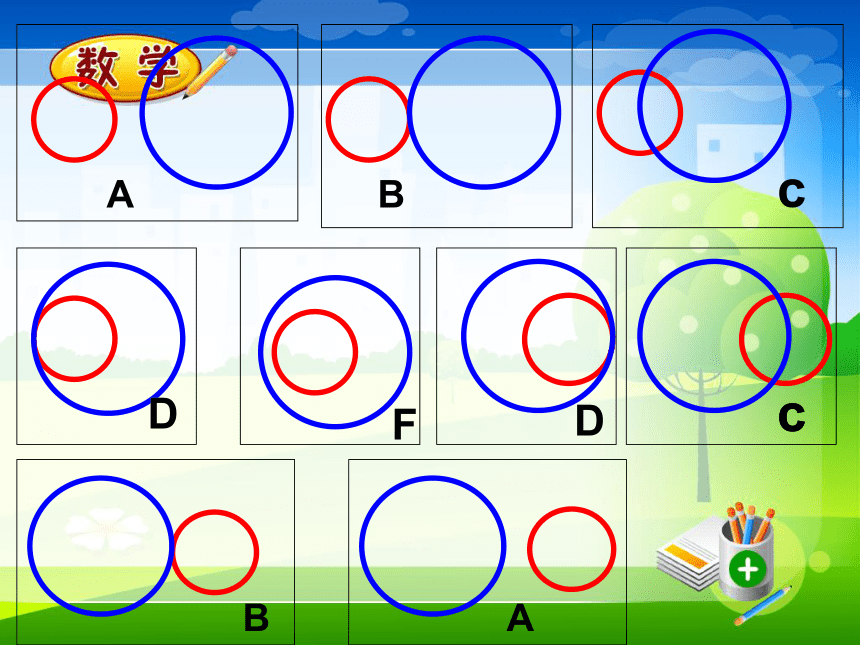
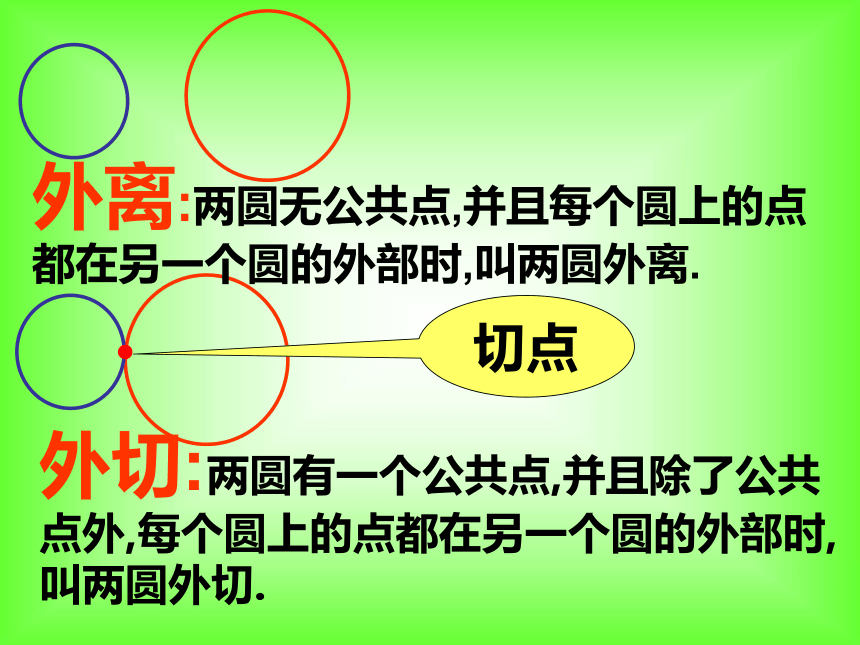
课件36张PPT。24.2.3日环食现象探究:圆和圆有哪几种位置关系? 认真观察观察结果AABBcccDDF外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离.外切:两圆有一个公共点,并且除了公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.切点切点相交:两圆有两个公共点时,叫两圆相交.内切:两圆有一个公共点,并且除了公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切.内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含..O同心圆圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交圆与圆的位置关系 1、判断正误:
(1)、若两圆只有一个交点,则这两圆外切. ( )
(2)、如果两圆没有交点,则这两圆的位置关系是外离. ( )
练一练××1、2008北京奥运会自行车比赛会标在 图中两圆的位置关系是___ __ 练一练外离2、在图中有两圆的多种位置关系,请你找出还没有的位置关系是 .相交一、点与圆的位置关系:(2)点在圆上(1)点在圆内(3)点在圆外
二、直线与圆的位置关系:d<r d=r d>r相离相切相交d>rd=rdR+r精彩源于发现外 离Rrdo1o2d=R+rT外 切o1o2rRdd=R-r (R>r)T内 切o1o2dRr相 交R-r (R>r)d=R+rd=R-rR-rr)OO1O20≤dr)内 含同心圆内切O2O1ddd=0d=R-r圆与圆的位置关系(从公共点个数看)(没有公共点)(有1个公共点)(有2个公共点)相离外离内含(同心圆)相切外切内切相交相交d>R+rd=R+r0≤dr)圆与圆的位置关系 2、⊙O1和⊙O2的半径分别为2cm和5cm,在下列情况下,分别求出两 圆的圆心距d的取值范围:
(1)外离 ________ (2)外切 ________ (3)相交 ____________(4)内切 ________ (5)内含___________ 练一练37d=7d=30 ≤d<31、判断题。
(1)、当O1O2=0时,两圆是同心圆. ( )
(2)、若O1O2=1.5,r=1,R=3,则O1O2 所以两圆相交. ( )
(3)、若O1O2=4,且r =3,R=7,则O1O2=
R-r,所以两圆内含. ( )√××
R=3 cm
R=13 cm
..PO 例3:如图⊙O的半径为5cm,点P是⊙O外一点,
OP=8cm。若以P为圆心作⊙P与⊙O相切,求⊙P的半径?
..PO综上⊙P的半径为3cm或13cm解:设⊙P的半径为R(1)若⊙O与⊙P外切,则 R =op-5=8-5则 R =8-5 (2)若⊙O与⊙P内切,则 R=OP+5=8,R5R5.882.已知两圆的半径分别为1厘米和5厘米,
(1)若两圆相交,则圆心距d的取值范围是 ;
(2)若两圆外离则d的取值范围 ;
(3)若两圆内含则d的取值范围 ;
若两圆相切则d= .口答:(看谁答得)460 ≤d<4d=4或61.已知两圆的半径分别为3厘米和2厘米,若两圆没有公共点,则圆心距d的取值范围为思考题
设两圆的半径分别为R、r,圆心距为d,若 R2 +r2-d2=2Rd,则这两圆的位置关系是( )
A. 内含 B. 内切 C. 相交 D.外切或内切思考题小结:1)两圆的五种位置关系2)用两圆的圆心距d与两圆的半径R,r的数量关系来判别两圆的位置关系图例名称d 与r 的数量关系drrddr点在圆内点在圆上点在圆外d < rd = rd > r点与圆的位置关系图例名称d 与 r
的数量
关系公共点个数drdrdr相离相切相交0个1个2个d < rd = rd > r直线与圆的位置关系再见 谢谢同学们的积极参与两圆位置关系的性质与判定:性质判定0R―rR+r同心圆内含外离 外切相交内切位 置 关 系 数 字 化d(六)、两圆位置关系的判定导航目标引入观察摆摆位置对称量量判定例题练习小结封底目录 封面
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交圆与圆的位置关系 1、判断正误:
(1)、若两圆只有一个交点,则这两圆外切. ( )
(2)、如果两圆没有交点,则这两圆的位置关系是外离. ( )
练一练××1、2008北京奥运会自行车比赛会标在 图中两圆的位置关系是___ __ 练一练外离2、在图中有两圆的多种位置关系,请你找出还没有的位置关系是 .相交一、点与圆的位置关系:(2)点在圆上(1)点在圆内(3)点在圆外
二、直线与圆的位置关系:d<r d=r d>r相离相切相交d>rd=rd
(1)外离 ________ (2)外切 ________ (3)相交 ____________(4)内切 ________ (5)内含___________ 练一练3
(1)、当O1O2=0时,两圆是同心圆. ( )
(2)、若O1O2=1.5,r=1,R=3,则O1O2
(3)、若O1O2=4,且r =3,R=7,则O1O2=
R-r,所以两圆内含. ( )√××
R=3 cm
R=13 cm
..PO 例3:如图⊙O的半径为5cm,点P是⊙O外一点,
OP=8cm。若以P为圆心作⊙P与⊙O相切,求⊙P的半径?
..PO综上⊙P的半径为3cm或13cm解:设⊙P的半径为R(1)若⊙O与⊙P外切,则 R =op-5=8-5则 R =8-5 (2)若⊙O与⊙P内切,则 R=OP+5=8,R5R5.882.已知两圆的半径分别为1厘米和5厘米,
(1)若两圆相交,则圆心距d的取值范围是 ;
(2)若两圆外离则d的取值范围 ;
(3)若两圆内含则d的取值范围 ;
若两圆相切则d= .口答:(看谁答得)4
设两圆的半径分别为R、r,圆心距为d,若 R2 +r2-d2=2Rd,则这两圆的位置关系是( )
A. 内含 B. 内切 C. 相交 D.外切或内切思考题小结:1)两圆的五种位置关系2)用两圆的圆心距d与两圆的半径R,r的数量关系来判别两圆的位置关系图例名称d 与r 的数量关系drrddr点在圆内点在圆上点在圆外d < rd = rd > r点与圆的位置关系图例名称d 与 r
的数量
关系公共点个数drdrdr相离相切相交0个1个2个d < rd = rd > r直线与圆的位置关系再见 谢谢同学们的积极参与两圆位置关系的性质与判定:性质判定0R―rR+r同心圆内含外离 外切相交内切位 置 关 系 数 字 化d(六)、两圆位置关系的判定导航目标引入观察摆摆位置对称量量判定例题练习小结封底目录 封面
同课章节目录
