2022-2023学年人教版九年级数学下册27.1图形的相似 强化练习 (无答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册27.1图形的相似 强化练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 191.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 22:34:51 | ||
图片预览

文档简介
27.1图形的相似强化练习
一、单选题
1、下列图形中,不一定是相似图形的是( )
A.两个等边三角形 B.两个等腰直角三角形
C.两个长方形 D.两个圆
2、若且,则的值为( )
A. B. C. D.
3、下列各组线段中,成比例的是( )
A.,,, B.,,,
C.,,, D.,,,
4、如图,C为线段AB的黄金分割点(AC<BC),且BC=2,则AB的长为( )
A.2+2 B.2﹣2 C.+1 D.﹣3
5. 一个五边形各边的边长为,,,,,另一个和它相似的五边形最长边为,则的最短边长为( )
A. B. C. D.
6. 已知平行四边形与平行四边形相似,,对应边,若平行四边形的面积为,则平行四边形的面积为( )
A. B. C. D.
7. 有同一三角形地块的甲,乙两地图,比例尺分别为:和:,那么甲地图与乙地图表示这一块的三角形面积比是( )
A. : B. : C. D.
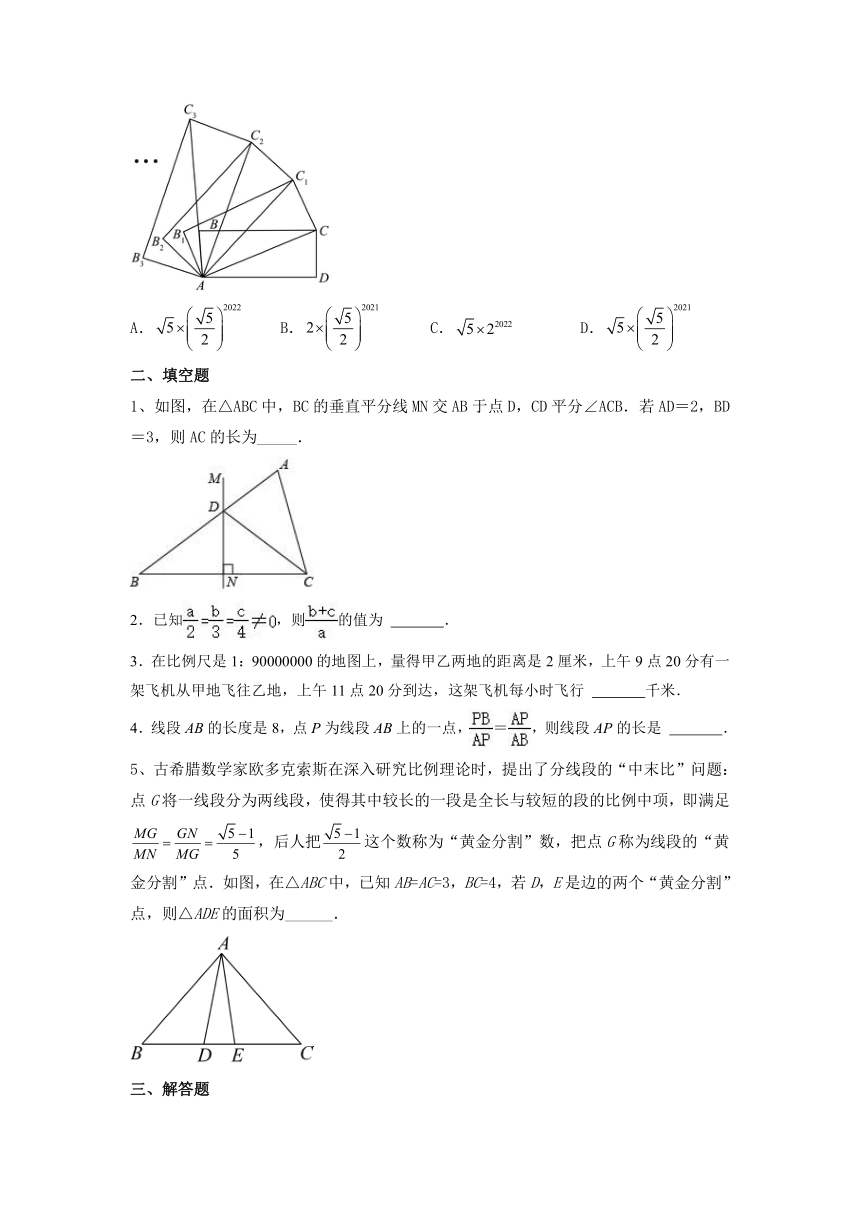
8、如图,在矩形ABCD中,,,连接AC,以对角线AC为边,按逆时针方向作矩形,使矩形矩形ADCB;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,…,按照此规律作下去,则边的长为( )
A. B. C. D.
二、填空题
1、如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为_____.
2.已知,则的值为 .
3.在比例尺是1:90000000的地图上,量得甲乙两地的距离是2厘米,上午9点20分有一架飞机从甲地飞往乙地,上午11点20分到达,这架飞机每小时飞行 千米.
4.线段AB的长度是8,点P为线段AB上的一点,=,则线段AP的长是 .
5、古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在△ABC中,已知AB=AC=3,BC=4,若D,E是边的两个“黄金分割”点,则△ADE的面积为______.
三、解答题
1、(1)已知线段是线段、的比例中项,如果,,求的长度.
(2)已知,求的值.
2.如图,已知点C是线段AB上的点,D是AB延长线上的点,且AB:BD=3:2,AC:BC=5:3,AC=10,求AD的长.
3.我们定义:顶角等于36°的等腰三角形为黄金三角形.如图,△ABC中,AB=AC且∠A=36°,则△ABC为黄金三角形.
(1)尺规作图:作∠B的角平分线,交AC于点D.(保留作图痕迹,不写作法)
(2)请判断△BDC是否为黄金三角形,如果是,请给出证明,如果不是,请说明理由.
4.书籍和纸张的长与宽比值都有固定的尺寸,如常用的A3、A4、A5的纸张长与宽的比值都相等.一长方形纸张对折后的小长方形的长与宽的比值与原长方形的长与宽的比值相等.
(1)求满足这样条件的长方形的长与宽的比值;
(2)如图所示的长方形ABCD长与宽之比也满足以上条件,其中宽AB=2.点P是AD上一点,将△BPA沿BP折叠得到△BPE,当BE垂直AC时,求AP的长.
5、如图,正比例函数与反比例函数的图象交于,两点.
(1)求,两点的坐标;
(2)将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点,与轴交于点,与轴交于点,若,求的值.
一、单选题
1、下列图形中,不一定是相似图形的是( )
A.两个等边三角形 B.两个等腰直角三角形
C.两个长方形 D.两个圆
2、若且,则的值为( )
A. B. C. D.
3、下列各组线段中,成比例的是( )
A.,,, B.,,,
C.,,, D.,,,
4、如图,C为线段AB的黄金分割点(AC<BC),且BC=2,则AB的长为( )
A.2+2 B.2﹣2 C.+1 D.﹣3
5. 一个五边形各边的边长为,,,,,另一个和它相似的五边形最长边为,则的最短边长为( )
A. B. C. D.
6. 已知平行四边形与平行四边形相似,,对应边,若平行四边形的面积为,则平行四边形的面积为( )
A. B. C. D.
7. 有同一三角形地块的甲,乙两地图,比例尺分别为:和:,那么甲地图与乙地图表示这一块的三角形面积比是( )
A. : B. : C. D.
8、如图,在矩形ABCD中,,,连接AC,以对角线AC为边,按逆时针方向作矩形,使矩形矩形ADCB;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,…,按照此规律作下去,则边的长为( )
A. B. C. D.
二、填空题
1、如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为_____.
2.已知,则的值为 .
3.在比例尺是1:90000000的地图上,量得甲乙两地的距离是2厘米,上午9点20分有一架飞机从甲地飞往乙地,上午11点20分到达,这架飞机每小时飞行 千米.
4.线段AB的长度是8,点P为线段AB上的一点,=,则线段AP的长是 .
5、古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在△ABC中,已知AB=AC=3,BC=4,若D,E是边的两个“黄金分割”点,则△ADE的面积为______.
三、解答题
1、(1)已知线段是线段、的比例中项,如果,,求的长度.
(2)已知,求的值.
2.如图,已知点C是线段AB上的点,D是AB延长线上的点,且AB:BD=3:2,AC:BC=5:3,AC=10,求AD的长.
3.我们定义:顶角等于36°的等腰三角形为黄金三角形.如图,△ABC中,AB=AC且∠A=36°,则△ABC为黄金三角形.
(1)尺规作图:作∠B的角平分线,交AC于点D.(保留作图痕迹,不写作法)
(2)请判断△BDC是否为黄金三角形,如果是,请给出证明,如果不是,请说明理由.
4.书籍和纸张的长与宽比值都有固定的尺寸,如常用的A3、A4、A5的纸张长与宽的比值都相等.一长方形纸张对折后的小长方形的长与宽的比值与原长方形的长与宽的比值相等.
(1)求满足这样条件的长方形的长与宽的比值;
(2)如图所示的长方形ABCD长与宽之比也满足以上条件,其中宽AB=2.点P是AD上一点,将△BPA沿BP折叠得到△BPE,当BE垂直AC时,求AP的长.
5、如图,正比例函数与反比例函数的图象交于,两点.
(1)求,两点的坐标;
(2)将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点,与轴交于点,与轴交于点,若,求的值.
