2022-2023学年北师大版七年级数学下册第四章 三角形 单元测试卷(含答案)
文档属性
| 名称 | 2022-2023学年北师大版七年级数学下册第四章 三角形 单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 23:12:21 | ||
图片预览

文档简介
第四章《三角形》单元测试卷
(新题型卷共23小题,满分120分,考试用时90分钟)
一、选择题(本大题共10小题,每小题3分,共30分)
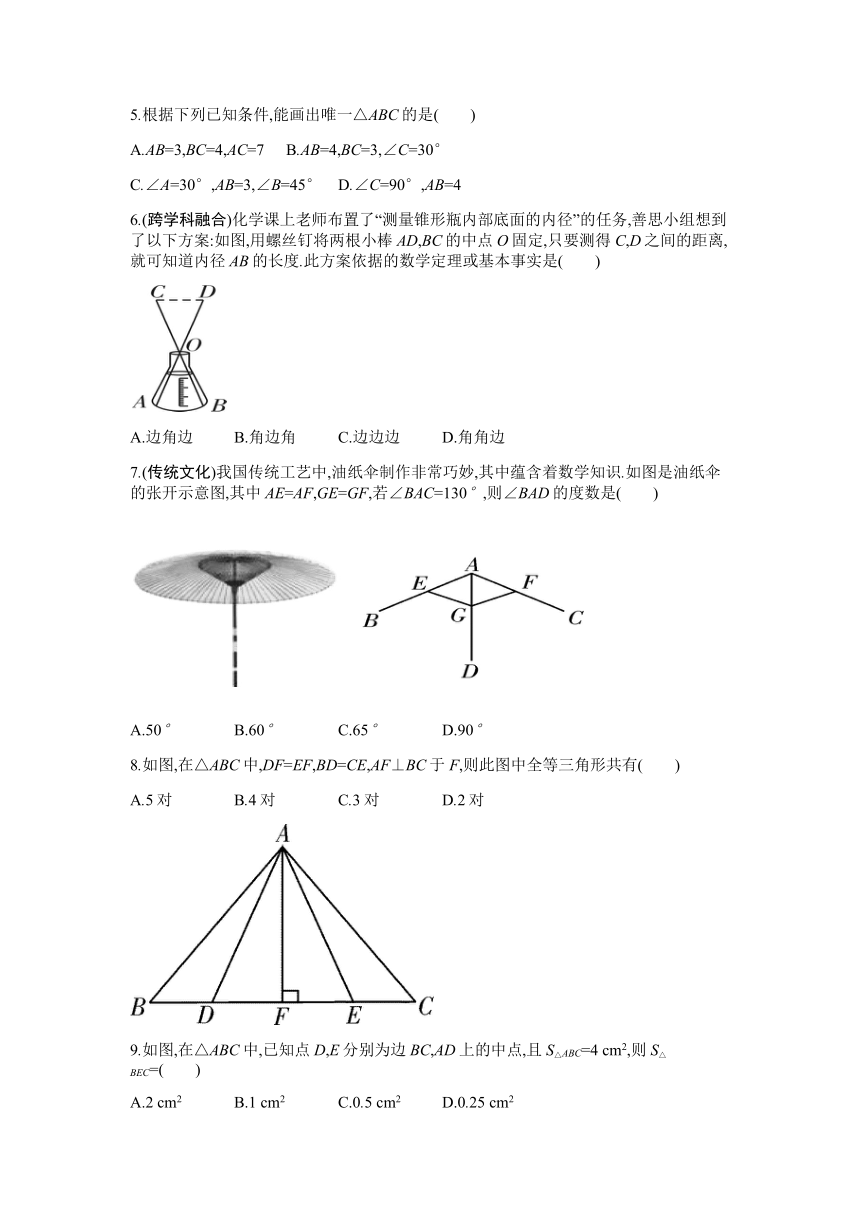
1.下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )
A.1,2,3 B.1,2,4 C.2,3,4 D.2,2,4
2.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A B C D
3.在△ABC中,∠A=36°,∠B∶∠C=1∶5,则∠C等于( )
A.120° B.100° C.24° D.20°
4.如图,若△ABC≌△DEF,BE=22,BF=5,则FC的长度是( )
A.10 B.12 C.8 D.16
5.根据下列已知条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,AC=7 B.AB=4,BC=3,∠C=30°
C.∠A=30°,AB=3,∠B=45° D.∠C=90°,AB=4
6.(跨学科融合)化学课上老师布置了“测量锥形瓶内部底面的内径”的任务,善思小组想到了以下方案:如图,用螺丝钉将两根小棒AD,BC的中点O固定,只要测得C,D之间的距离,就可知道内径AB的长度.此方案依据的数学定理或基本事实是( )
A.边角边 B.角边角 C.边边边 D.角角边
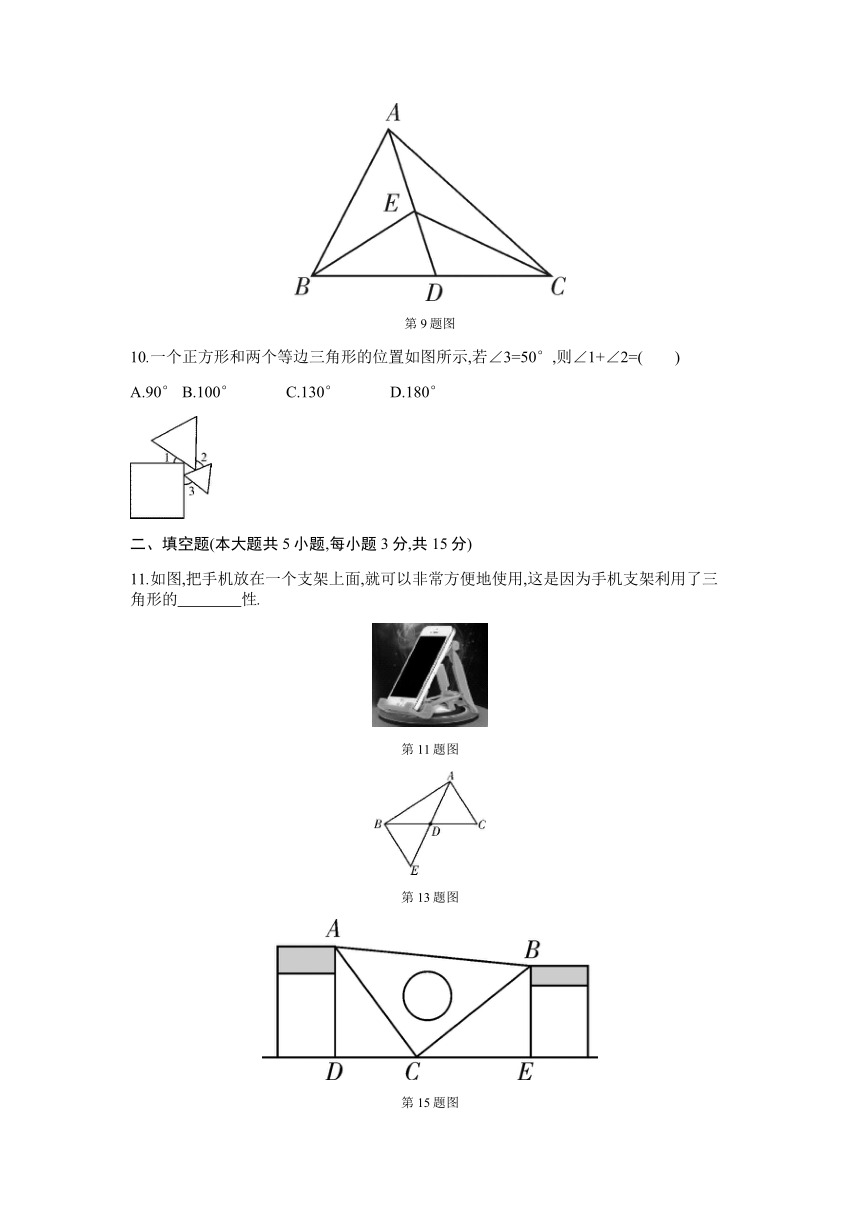
7.(传统文化)我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识.如图是油纸伞的张开示意图,其中AE=AF,GE=GF,若∠BAC=130°,则∠BAD的度数是( )
A.50° B.60° C.65° D.90°
8.如图,在△ABC中,DF=EF,BD=CE,AF⊥BC于F,则此图中全等三角形共有( )
A.5对 B.4对 C.3对 D.2对
9.如图,在△ABC中,已知点D,E分别为边BC,AD上的中点,且S△ABC=4 cm2,则S△BEC=( )
A.2 cm2 B.1 cm2 C.0.5 cm2 D.0.25 cm2
第9题图
10.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
A.90° B.100° C.130° D.180°
二、填空题(本大题共5小题,每小题3分,共15分)
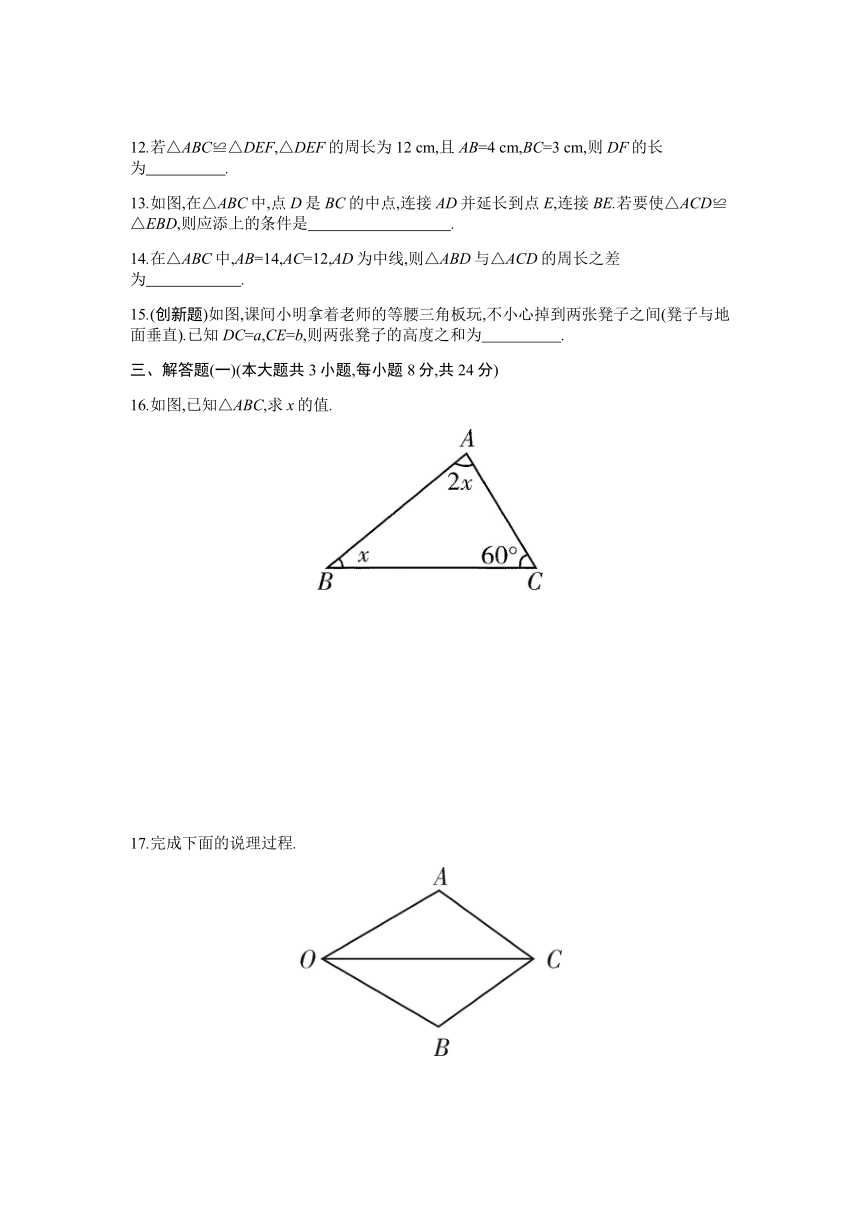
11.如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的 性.
第11题图
第13题图
第15题图
12.若△ABC≌△DEF,△DEF的周长为12 cm,且AB=4 cm,BC=3 cm,则DF的长为 .
13.如图,在△ABC中,点D是BC的中点,连接AD并延长到点E,连接BE.若要使△ACD≌△EBD,则应添上的条件是 .
14.在△ABC中,AB=14,AC=12,AD为中线,则△ABD与△ACD的周长之差为 .
15.(创新题)如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两张凳子的高度之和为 .
三、解答题(一)(本大题共3小题,每小题8分,共24分)
16.如图,已知△ABC,求x的值.
17.完成下面的说理过程.
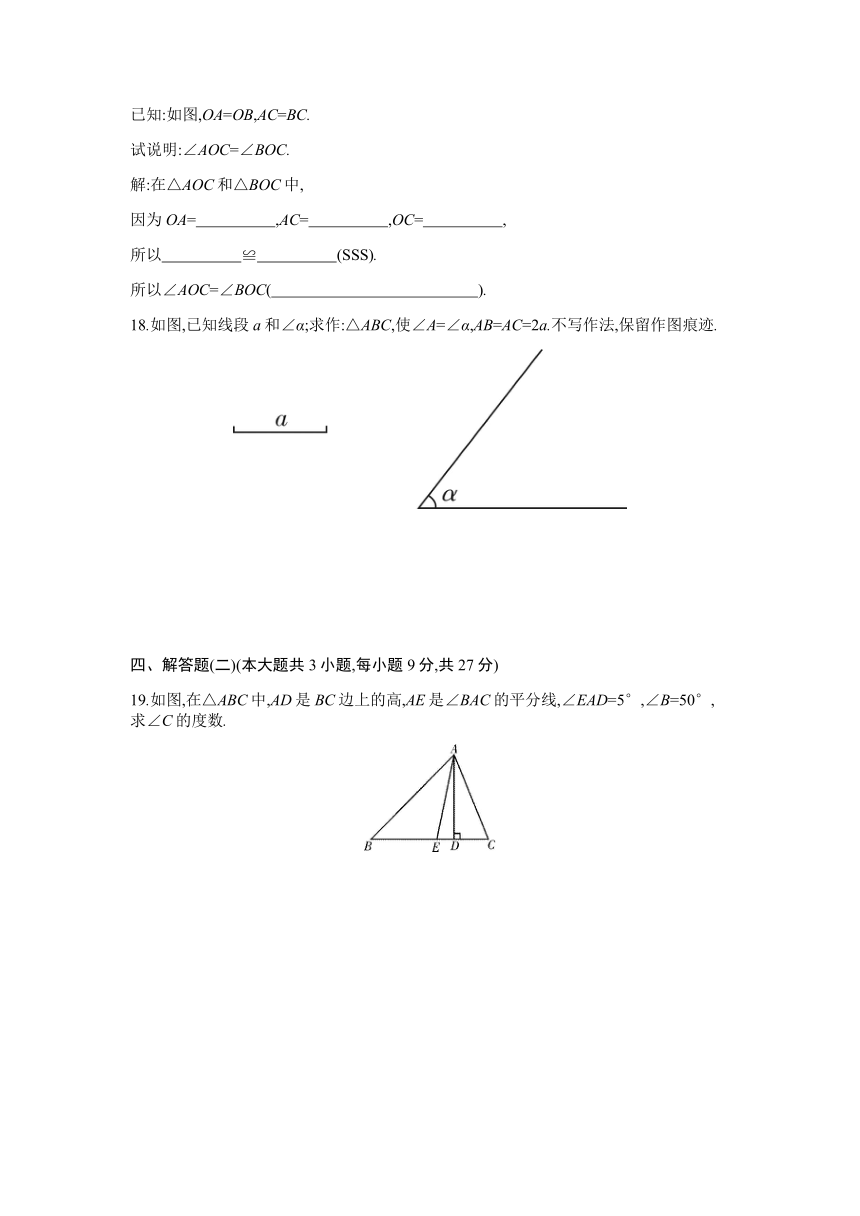
已知:如图,OA=OB,AC=BC.
试说明:∠AOC=∠BOC.
解:在△AOC和△BOC中,
因为OA= ,AC= ,OC= ,
所以 ≌ (SSS).
所以∠AOC=∠BOC( ).
18.如图,已知线段a和∠α;求作:△ABC,使∠A=∠α,AB=AC=2a.不写作法,保留作图痕迹.
四、解答题(二)(本大题共3小题,每小题9分,共27分)
19.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
20.如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.试说明:△CED≌△ABC.
21.如图,AB=AD,AC=AE,BC=DE,点E在BC上.
(1)试说明:△ABC≌△ADE;
(2)试说明:∠EAC=∠DEB.
五、解答题(三)(本大题共2小题,每小题12分,共24分)
22.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
23.如图,在四边形ABCD中,AB=10 cm,BC=8 cm,CD=12 cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3 cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1 s后,△BPE与△CQP是否全等 请说明理由;
(2)若点Q与点P的运动速度不同,当点Q的运动速度为多少时,能够使△BEP与△CQP全等
第四章《三角形》单元测试卷
1.C 2.A 3.A 4.B 5.C 6.A 7.C 8.B 9.A 10.B
11.稳定 12.5 cm 13.AD=DE(答案不唯一)
14.2 15.a+b
16.解:由图可得x+2x+60°=180°,解得x=40°.
17.OB BC OC △AOC △BOC
全等三角形的对应角相等
18.解:所求作△ABC如图所示.
19.解:因为AD是BC边上的高,所以∠ADB=90°.
因为∠B=50°,所以∠BAD=90°-50°=40°,
所以∠BAE=∠BAD-∠EAD=40°-5°=35°.
因为AE是∠BAC的平分线,
所以∠BAC=2∠BAE=70°,
所以∠C=180°-∠B-∠BAC=180°-50°-70°=60°.
20.解:因为DE⊥AC,∠B=90°,所以∠DEC=∠B=90°.
因为CD∥AB,所以∠A=∠DCE.
在△CED和△ABC中,,
所以△CED≌△ABC(ASA).
21.解:(1)因为AB=AD,AC=AE,BC=DE,
所以△ABC≌△ADE(SSS).
(2)因为△ABC≌△ADE,
所以∠D=∠B,∠DAE=∠BAC.
所以∠DAE-∠BAE=∠BAC-∠BAE,即∠DAB=∠EAC.
设AB和DE交于点O,因为∠DOA=∠BOE,∠D=∠B,
所以∠DEB=∠DAB,所以∠EAC=∠DEB.
22.解:(1)因为∠A+∠B+∠C=180°,
所以∠A=180°-(∠B+∠C)=180°-(50°+60°)=70°.
(2)因为△A'DE是△ADE翻折变换而成的,
所以∠AED=∠A'ED,∠ADE=∠A'DE,∠A=∠A',
所以∠AED+∠ADE=∠A'ED+∠A'DE=180°-∠A,
所以∠1+∠2=360°-2(180°-∠A)=2∠A,
所以∠A=(∠1+∠2)=×130°=65°.
23.解:(1)全等,理由如下:
当运动1 s后,则BP=CQ=3 cm,
所以PC=BC-BP=8-3=5(cm).
因为E为AB的中点,且AB=10 cm,
所以BE=5 cm,所以BE=PC.
在△BPE和△CQP中,
所以△BPE≌△CQP(SAS).
(2)当△BEP≌△CQP时,则BP=CP,CQ=BE=5 cm,
设点P的运动时间为t s,则3t=8-3t,解得t=,
所以点Q的速度=5÷(cm/s),
即当点Q每秒运动 cm时,△BEP≌△CQP.
(新题型卷共23小题,满分120分,考试用时90分钟)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )
A.1,2,3 B.1,2,4 C.2,3,4 D.2,2,4
2.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A B C D
3.在△ABC中,∠A=36°,∠B∶∠C=1∶5,则∠C等于( )
A.120° B.100° C.24° D.20°
4.如图,若△ABC≌△DEF,BE=22,BF=5,则FC的长度是( )
A.10 B.12 C.8 D.16
5.根据下列已知条件,能画出唯一△ABC的是( )
A.AB=3,BC=4,AC=7 B.AB=4,BC=3,∠C=30°
C.∠A=30°,AB=3,∠B=45° D.∠C=90°,AB=4
6.(跨学科融合)化学课上老师布置了“测量锥形瓶内部底面的内径”的任务,善思小组想到了以下方案:如图,用螺丝钉将两根小棒AD,BC的中点O固定,只要测得C,D之间的距离,就可知道内径AB的长度.此方案依据的数学定理或基本事实是( )
A.边角边 B.角边角 C.边边边 D.角角边
7.(传统文化)我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识.如图是油纸伞的张开示意图,其中AE=AF,GE=GF,若∠BAC=130°,则∠BAD的度数是( )
A.50° B.60° C.65° D.90°
8.如图,在△ABC中,DF=EF,BD=CE,AF⊥BC于F,则此图中全等三角形共有( )
A.5对 B.4对 C.3对 D.2对
9.如图,在△ABC中,已知点D,E分别为边BC,AD上的中点,且S△ABC=4 cm2,则S△BEC=( )
A.2 cm2 B.1 cm2 C.0.5 cm2 D.0.25 cm2
第9题图
10.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
A.90° B.100° C.130° D.180°
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的 性.
第11题图
第13题图
第15题图
12.若△ABC≌△DEF,△DEF的周长为12 cm,且AB=4 cm,BC=3 cm,则DF的长为 .
13.如图,在△ABC中,点D是BC的中点,连接AD并延长到点E,连接BE.若要使△ACD≌△EBD,则应添上的条件是 .
14.在△ABC中,AB=14,AC=12,AD为中线,则△ABD与△ACD的周长之差为 .
15.(创新题)如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两张凳子的高度之和为 .
三、解答题(一)(本大题共3小题,每小题8分,共24分)
16.如图,已知△ABC,求x的值.
17.完成下面的说理过程.
已知:如图,OA=OB,AC=BC.
试说明:∠AOC=∠BOC.
解:在△AOC和△BOC中,
因为OA= ,AC= ,OC= ,
所以 ≌ (SSS).
所以∠AOC=∠BOC( ).
18.如图,已知线段a和∠α;求作:△ABC,使∠A=∠α,AB=AC=2a.不写作法,保留作图痕迹.
四、解答题(二)(本大题共3小题,每小题9分,共27分)
19.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
20.如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.试说明:△CED≌△ABC.
21.如图,AB=AD,AC=AE,BC=DE,点E在BC上.
(1)试说明:△ABC≌△ADE;
(2)试说明:∠EAC=∠DEB.
五、解答题(三)(本大题共2小题,每小题12分,共24分)
22.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
23.如图,在四边形ABCD中,AB=10 cm,BC=8 cm,CD=12 cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3 cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1 s后,△BPE与△CQP是否全等 请说明理由;
(2)若点Q与点P的运动速度不同,当点Q的运动速度为多少时,能够使△BEP与△CQP全等
第四章《三角形》单元测试卷
1.C 2.A 3.A 4.B 5.C 6.A 7.C 8.B 9.A 10.B
11.稳定 12.5 cm 13.AD=DE(答案不唯一)
14.2 15.a+b
16.解:由图可得x+2x+60°=180°,解得x=40°.
17.OB BC OC △AOC △BOC
全等三角形的对应角相等
18.解:所求作△ABC如图所示.
19.解:因为AD是BC边上的高,所以∠ADB=90°.
因为∠B=50°,所以∠BAD=90°-50°=40°,
所以∠BAE=∠BAD-∠EAD=40°-5°=35°.
因为AE是∠BAC的平分线,
所以∠BAC=2∠BAE=70°,
所以∠C=180°-∠B-∠BAC=180°-50°-70°=60°.
20.解:因为DE⊥AC,∠B=90°,所以∠DEC=∠B=90°.
因为CD∥AB,所以∠A=∠DCE.
在△CED和△ABC中,,
所以△CED≌△ABC(ASA).
21.解:(1)因为AB=AD,AC=AE,BC=DE,
所以△ABC≌△ADE(SSS).
(2)因为△ABC≌△ADE,
所以∠D=∠B,∠DAE=∠BAC.
所以∠DAE-∠BAE=∠BAC-∠BAE,即∠DAB=∠EAC.
设AB和DE交于点O,因为∠DOA=∠BOE,∠D=∠B,
所以∠DEB=∠DAB,所以∠EAC=∠DEB.
22.解:(1)因为∠A+∠B+∠C=180°,
所以∠A=180°-(∠B+∠C)=180°-(50°+60°)=70°.
(2)因为△A'DE是△ADE翻折变换而成的,
所以∠AED=∠A'ED,∠ADE=∠A'DE,∠A=∠A',
所以∠AED+∠ADE=∠A'ED+∠A'DE=180°-∠A,
所以∠1+∠2=360°-2(180°-∠A)=2∠A,
所以∠A=(∠1+∠2)=×130°=65°.
23.解:(1)全等,理由如下:
当运动1 s后,则BP=CQ=3 cm,
所以PC=BC-BP=8-3=5(cm).
因为E为AB的中点,且AB=10 cm,
所以BE=5 cm,所以BE=PC.
在△BPE和△CQP中,
所以△BPE≌△CQP(SAS).
(2)当△BEP≌△CQP时,则BP=CP,CQ=BE=5 cm,
设点P的运动时间为t s,则3t=8-3t,解得t=,
所以点Q的速度=5÷(cm/s),
即当点Q每秒运动 cm时,△BEP≌△CQP.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
