2022-2023学年八年级下学期沪教版数学第二十章一次函数专项训练(含解析)
文档属性
| 名称 | 2022-2023学年八年级下学期沪教版数学第二十章一次函数专项训练(含解析) |  | |
| 格式 | |||
| 文件大小 | 881.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-21 08:57:15 | ||
图片预览


文档简介
八年级数学第二学期第二十章一次函数专项训练
考试时间:90 分钟;命题人:数学教研组
考生注意:
1、本卷分第 I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100 分,考试时间90 分钟
2、答卷前,考生务必用0.5 毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新
的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第 I 卷(选择题 30 分)
一、单选题(10 小题,每小题 3分,共计 30 分)
1、如果函数 y=(2﹣k)x+5 是关于 x的一次函数,且 y随 x的值增大而减小,那么 k的取值范围是
( )
A.k≠0 B.k<2 C.k>2 D.k≠2
2、若点(-3,y )、(2,y )都在函数 y=-4x+b的图像上,则 y 与 y 的大小关系( )
1 2 1 2
A.y>y B.y<y C.y=y D.无法确定
1 2 1 2 1 2
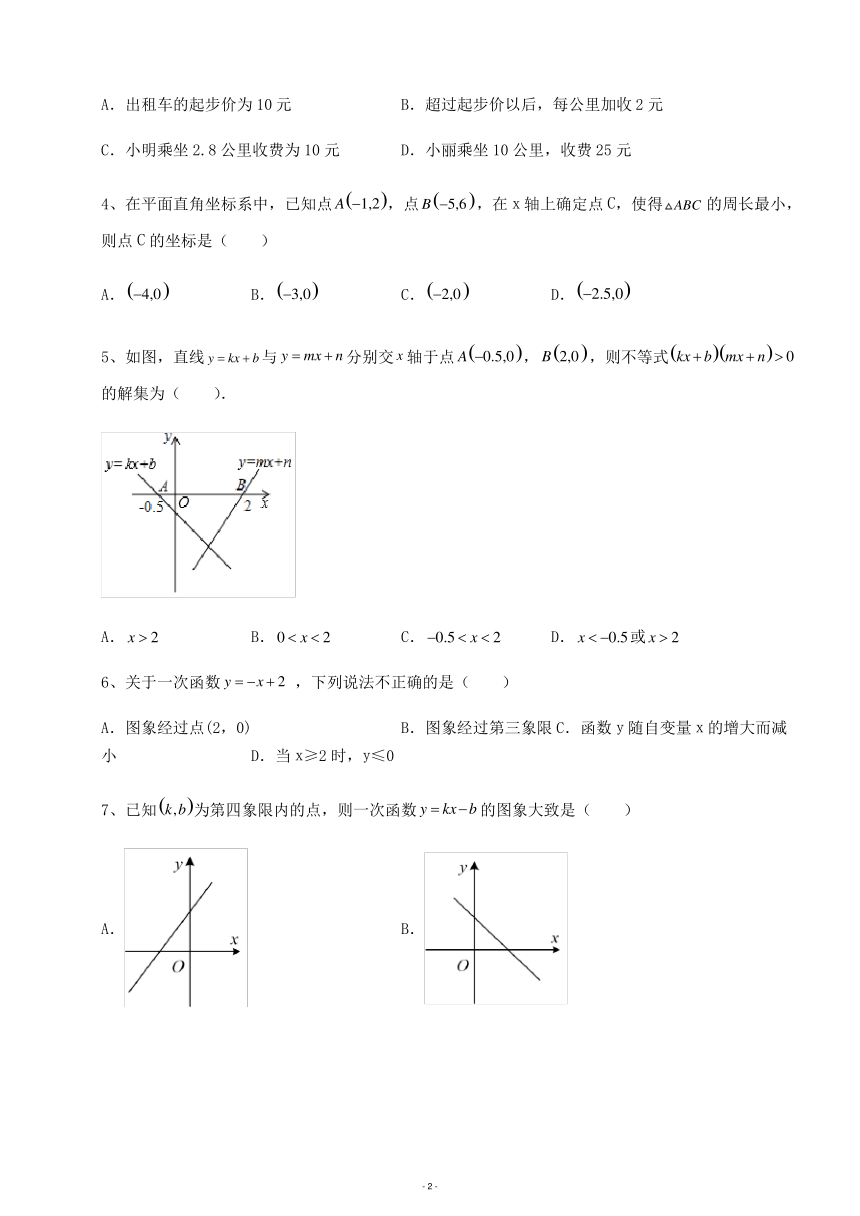
3、自 2021 年 9月 16 日起,合肥市出租车价格调整,调整后的价格如图所示,根据图中的数据,下
列说法不正确的是( )
- 1 -
A.出租车的起步价为 10元 B.超过起步价以后,每公里加收2元
C.小明乘坐 2.8 公里收费为 10 元 D.小丽乘坐 10公里,收费 25 元
4、在平面直角坐标系中,已知点 A 1,2 ,点B 5,6 ,在 x轴上确定点 C,使得 ABC 的周长最小,
则点 C的坐标是( )
A. 4,0 B. 3,0 C. 2,0 D. 2.5,0
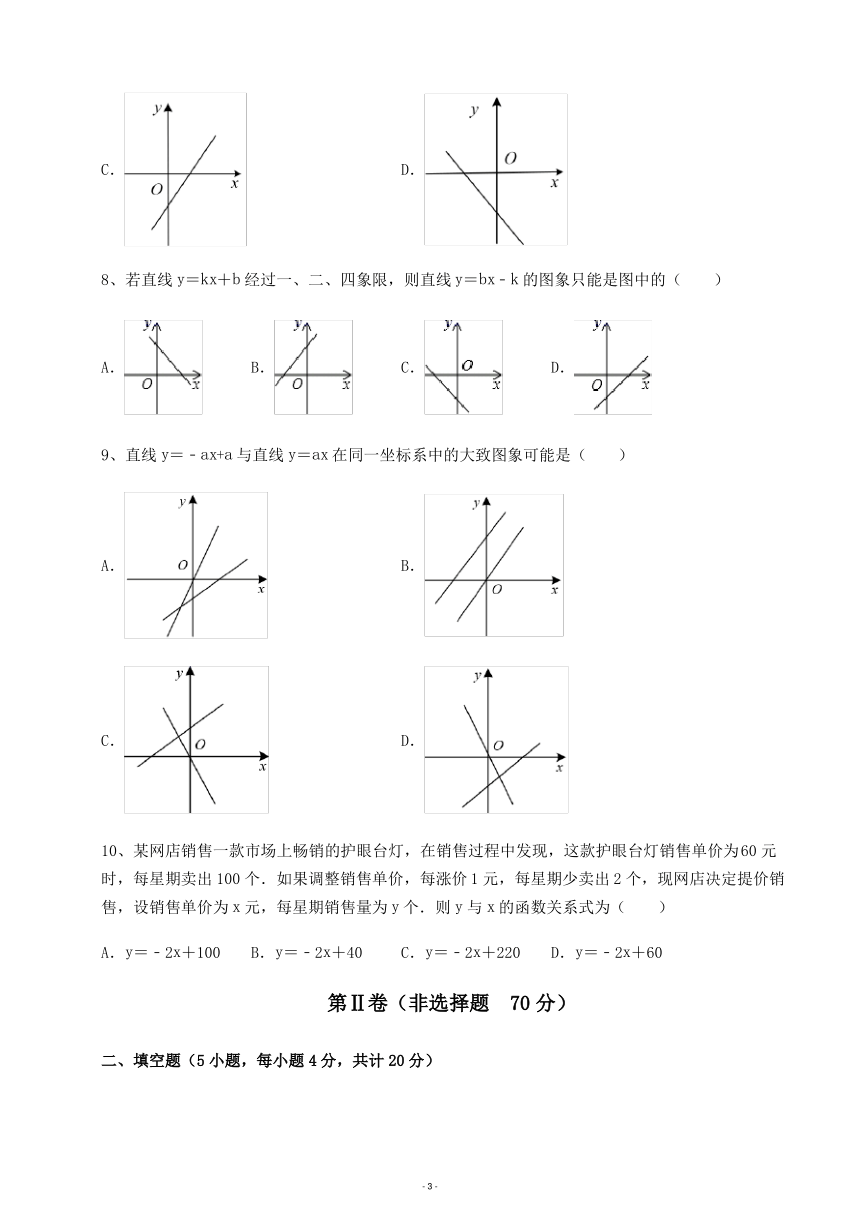
5、如图,直线 y kx b与 y mx n分别交 x轴于点 A 0.5,0 ,B 2,0 ,则不等式 kx b mx n 0
的解集为( ).
A. x 2 B.0 x 2 C. 0.5 x 2 D. x 0.5或 x 2
6、关于一次函数 y x 2 ,下列说法不正确的是( )
A.图象经过点(2,0) B.图象经过第三象限 C.函数 y随自变量 x的增大而减
小 D.当 x≥2时,y≤0
7、已知 k,b 为第四象限内的点,则一次函数 y kx b的图象大致是( )
A. B.
- 2 -
C. D.
8、若直线 y=kx+b经过一、二、四象限,则直线 y=bx﹣k的图象只能是图中的( )
A. B. C. D.
9、直线 y=﹣ax+a与直线 y=ax在同一坐标系中的大致图象可能是( )
A. B.
C. D.
10、某网店销售一款市场上畅销的护眼台灯,在销售过程中发现,这款护眼台灯销售单价为60 元
时,每星期卖出 100 个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销
售,设销售单价为 x元,每星期销售量为 y个.则 y与 x的函数关系式为( )
A.y=﹣2x+100 B.y=﹣2x+40 C.y=﹣2x+220 D.y=﹣2x+60
第Ⅱ卷(非选择题 70 分)
二、填空题(5小题,每小题 4分,共计 20 分)
- 3 -
1、如图,在平面直角坐标系中,一次函数 y=-2x+4 的图像与 x轴、y轴分别交于点 A、B,将直线
AB绕点 B顺时针旋转 45°,交 x轴于点 C,则直线 BC的函数表达式为_______.
2、一次函数 y=(m-1)x+2 的函数值 y随 x的增大而增大,则 m的取值范围是_____.
3、已知一次函数 y kx 4 k 0 的图象与两坐标轴围成的三角形面积为4,则 k ______.
4、一次函数 y=kx+b(k≠0)中两个变量 x、y的部分对应值如下表所示:
x … -2 -1 0 1 2 …
y … 8 5 2 -1 -4 …
那么关于 x的不等式 kx+b≥-1的解集是________.
5、若一次函数 y=kx+8(k≠0)的图象与 x轴、y轴分别交于 A、B两点,当 k的取值变化时,点 A
随之在 x轴上运动,将线段 AB绕点 B逆时针旋转90°得到 BQ,连接 OQ,则 OQ长的最小值是 ___.
三、解答题(5小题,每小题 10 分,共计 50 分)
1、成都市某在建地铁工程需要将一批水泥运送到施工现场,现有甲、乙两种货车可以租用.已知2
辆甲种货车和 3辆乙种货车一次可运送46吨水泥,1辆甲种货车和 2辆乙种货车一次可运送28 吨水
泥.
(1)求每辆甲种货车和每辆乙种货车一次分别能装运多少吨水泥?
(2)已知甲种货车每辆租金为450 元,乙种货车每辆租金为400 元,现租用甲、乙共9辆货车.请
求出租用货车的总费用W (元)与租用甲种货车的数量a (辆)之间的函数关系式.
(3)在(2)的条件下,为了保障能拉完这批水泥,发现甲种货车不少于5辆,请你为该企业设计如
何租车费用最少?并求出最少费用是多少元?
- 4 -
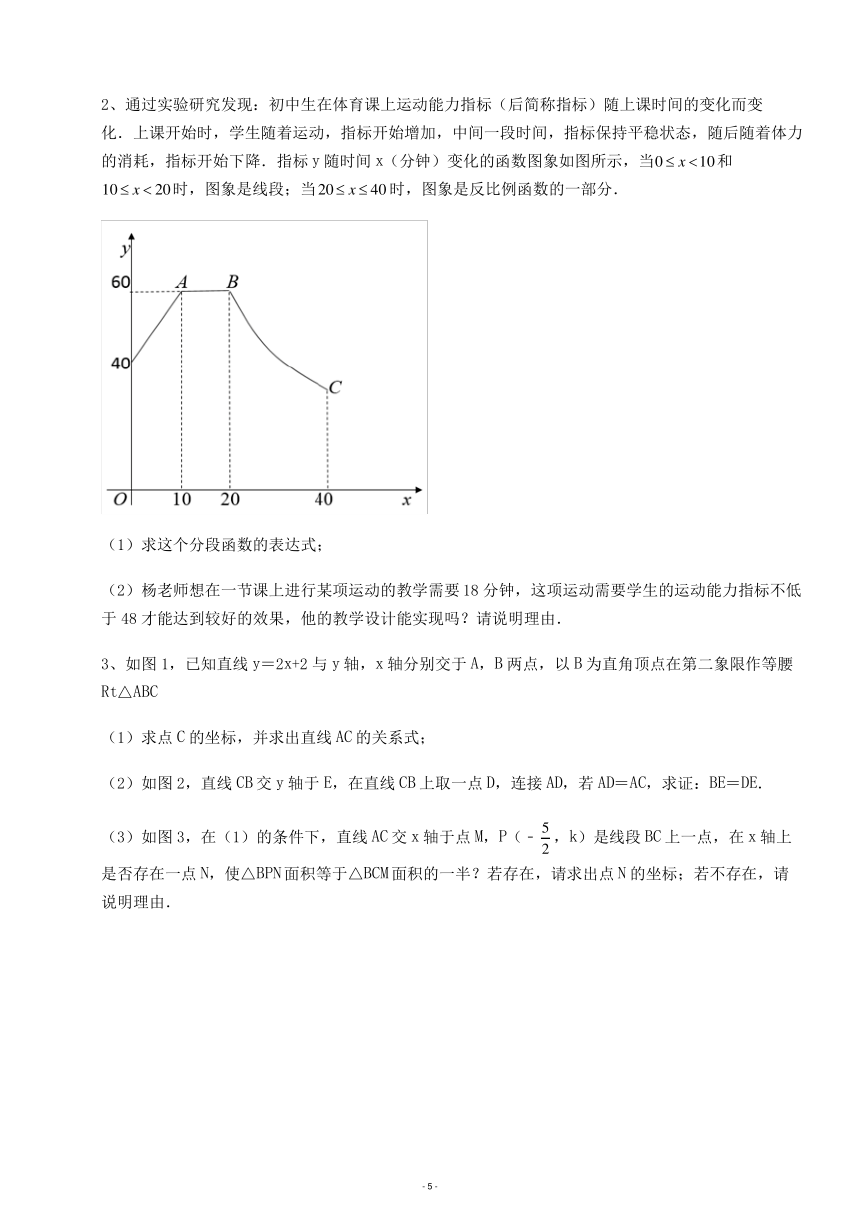
2、通过实验研究发现:初中生在体育课上运动能力指标(后简称指标)随上课时间的变化而变
化.上课开始时,学生随着运动,指标开始增加,中间一段时间,指标保持平稳状态,随后随着体力
的消耗,指标开始下降.指标 y随时间 x(分钟)变化的函数图象如图所示,当0 x 10和
10 x 20时,图象是线段;当20 x 40时,图象是反比例函数的一部分.
(1)求这个分段函数的表达式;
(2)杨老师想在一节课上进行某项运动的教学需要18 分钟,这项运动需要学生的运动能力指标不低
于 48 才能达到较好的效果,他的教学设计能实现吗?请说明理由.
3、如图 1,已知直线 y=2x+2 与 y轴,x轴分别交于 A,B两点,以 B为直角顶点在第二象限作等腰
Rt△ABC
(1)求点 C的坐标,并求出直线 AC的关系式;
(2)如图 2,直线 CB交 y轴于 E,在直线 CB上取一点 D,连接 AD,若 AD=AC,求证:BE=DE.
5
(3)如图 3,在(1)的条件下,直线 AC交 x轴于点 M,P(﹣ ,k)是线段 BC上一点,在 x轴上
2
是否存在一点 N,使△BPN面积等于△BCM面积的一半?若存在,请求出点 N的坐标;若不存在,请
说明理由.
- 5 -
4、若 y﹣2与 2x+3 成正比例,且当 x=1时,y=12.
(1)求 y与 x的函数解析式.
(2)求当 x=1时,函数 y的值.
5、如图,在平面直角坐标系中,点 A为 y轴正半轴上一点,点 B为 x轴负半轴上一点,点 C为 x轴
正半轴上一点,OA=OB=m,OC=n,满足 m2﹣12m+36+(n﹣2)2=0,作 BD⊥AC于 D,BD交 OA于
E.
(1)如图 1,求点 B、C的坐标;
(2)如图 2,动点 P从 B点出发,以每秒 2个单位的速度沿 x轴向右运动,设点 P运动的时间为 t,
△PEC的面积为 S,请用含 t的式子表示 S,并直接写出 t的取值范围;
(3)如图 3,在(2)的条件下,当 t=6时,在坐标平面内是否存在点 F,使△PEF是以 PE为底边
的等腰直角三角形,若存在,求出点 F的坐标,若不存在,请说明理由.
- 6 -
-参考答案-
一、单选题
1、C
【分析】
由题意 y 2 k x 5,y随x的增大而减小,可得自变量系数小于 0,进而可得 k 的范围.
【详解】
解:∵关于x的一次函数 y 2 k x 5的函数值 y随着 x的增大而减小,
2 k 0,
k 2.
故选 C.
【点睛】
本题主要考查了一次函数的增减性问题,解题的关键是:掌握在 y kx b中,k 0, y 随 x的增大而
增大,k 0, y随x的增大而减小.
2、A
【分析】
根据一次函数的性质得出 y随 x的增大而减小,进而求解.
【详解】
由一次函数 y=-4x+b可知,k=-4<0,y随x的增大而减小,
∵-3<2,
∴y>y,
1 2
故选:A.
【点睛】
本题考查一次函数的性质,熟知一次函数 y=kx+b(k≠0),当 k<0时,y随 x 的增大而减小是解题
的关键.
3、C
【分析】
根据(5,15),(7,19),确定函数的解析式,计算 y=10 时,x的值,结合生活实际,解答即可.
【详解】
设起步价以后函数的解析式为 y=kx+b,
5k b=15
把(5,15),(7,19)代入解析式,得 ,
7k+b 19
k 2
解得 ,
b 5
∴y=2x+5,
当 y=10 时,x=2.5,
当 x=10 时,y=25,
∴C错误,D正确,B正确,A正确,
故选 C.
【点睛】
本题考查了一次函数的实际应用,熟练掌握待定系数法,理解生活意义是解题的关键.
4、C
【分析】
因为 AB的长度是确定的,故△CAB的周长最小就是 CA+CB的值最小,作点 A关于 x轴的对称点 A′,
连接 A′B交 x轴于点 C,求出 C点坐标即可.
【详解】
解:如图,作点 A关于 x轴的对称点 A′,连接 A′B交 x轴于点 C,此时,AC+BC=A′C+BC=AC,长度
最小,
∵A(-1,2),
∴A′(-1,﹣2),
设直线 A′B的解析式为 y=kx+b(k≠0),把 A′(-1,﹣2),B 5,6 代入得,
5k b 6 k 2
∴ ,解得 ,
k b 2 b 4
∴直线 A′B的解析式为 y=-2x﹣4,
当 y=0时,x=-2,
∴C(-2,0).
故选:C
【点睛】
本题考查了轴对称-最短路径问题,一次函数与坐标轴交点问题,解题关键是确定点C的位置,利用
一次函数解析式求坐标.
5、C
【分析】
观察图象,可知当 x< - 0.5 时,y=kx+b>0,y=mx+n<0;当 - 0.5<x<2时,y=kx+b<0,y=mx+n<
0;当 x>2时,y=kx+b<0,y=mx+n>0,二者相乘为正的范围是本题的解集.
【详解】
解:由图象可得,
当 x>2时,(kx+b)<0,(mx+n)>0,则(kx+b)(mx+n)<0,故 A错误;
当 0<x<2时,kx+b<0,mx+n<0,(kx+b)(mx+n)>0,但是没有包含所有使得(kx+b)(mx+n)>
0的解集,故 B错误;
当 0.5 x 2时,kx+b<0,mx+n<0,故(kx+b)(mx+n)>0,且除此范围之外都不能使得(kx+b)
(mx+n)>0,故 C正确;
当 x<- 0.5 时,y=kx+b>0,y=mx+n<0;当 x>2时,y=kx+b<0,y=mx+n>0,则(kx+b)(mx+n)
<0,故 D错误;
故选:C.
【点睛】
本题考查了利用函数图象来解一元一次不等式,数形结合是解答本题的关键.
6、B
【分析】
当 y 0 时, x 2 ,可得图象经过点(2,0);再由 1 0,2 0 ,可得图象经过第一、二、四象限;
函数 y随自变量 x的增大而减小;然后根据 x 2 时, y 0 ,可得当 x≥2时,y≤0,即可求解.
【详解】
解:当 y 0 时, x 2 ,
∴图象经过点(2,0),故 A正确,不符合题意;
∵ 1 0,2 0 ,
∴图象经过第一、二、四象限,故B错误,符合题意;
∴函数 y随自变量 x的增大而减小,故C正确,不符合题意;
当 x 2 时, y 0 ,
∴当 x≥2时,y≤0,故 D正确,不符合题意;
故选:B
【点睛】
本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键.
7、A
【分析】
根据 k,b 为第四象限内的点,可得k 0,b 0 ,从而得到 b 0 ,进而得到一次函数 y kx b的图
象经过第一、二、三象限,即可求解.
【详解】
解:∵ k,b 为第四象限内的点,
∴ k 0,b 0 ,
∴ b 0 ,
∴一次函数 y kx b的图象经过第一、二、三象限.
故选:A
【点睛】
本题主要考查了坐标与图形,一次函数的图象,熟练掌握一次函数y kx b k 0 ,当 k 0,b 0
时,一次函数图象经过第一、二、三象限;当k 0,b 0时,一次函数图象经过第一、三、四象限;
当 k 0,b 0时,一次函数图象经过第一、二、四象限;当k 0,b 0时,一次函数图象经过第二、
三、四象限是解题的关键.
8、B
【分析】
根据直线 y=kx+b经过一、二、四象限,可得 k<0,b>0,从而得到直线 y=bx﹣k过一、二、三
象限,即可求解.
【详解】
解:∵直线 y=kx+b经过一、二、四象限,
∴k<0,b>0,
∴﹣k>0,
∴直线 y=bx﹣k过一、二、三象限,
∴选项 B中图象符合题意.
故选:B
【点睛】
本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键.
9、D
【分析】
若 y=ax过第一、三象限,则 a>0,所以 y=-ax+a过第一、二、四象限,可对A、B进行判断;若
y=ax过第二、四象限,则 a<0,-a>0,,所以 y=-ax+a过第一、三、四象限,与 y轴的交点在 y轴
负半轴,则可对 C、D进行判断.
【详解】
解:A、y=ax过第一、三象限,则 a>0,所以 y=-ax+a过第一、二、四象限,所以A选项不符合题
意;
B、y=ax过第一、三象限,则 a>0,所以 y=-ax+a过第一、二、四象限,所以B选项不符合题意;
C、y=ax过第二、四象限,则 a<0,-a>0,所以 y=-ax+a过第一、三、四象限,与 y轴的交点在 y
轴负半轴,所以 C选项不符合题意;
D、y=ax过第二、四象限,则 a<0,-a>0,所以 y=-ax+a过第一、三、四象限,与 y轴的交点在 y
轴负半轴,所以 D选项符合题意;
故选 D.
【点睛】
本题考查了一次函数的图象:一次函数 y=kx+b(k≠0)的图象为一条直线,当 k>0,图象过第一、
三象限;当 k<0,图象过第二、四象限;直线与 y轴的交点坐标为(0,b).
10、C
【分析】
根据单价为 60 元时,每星期卖出100 个,每涨价 1元,每星期少卖出 2个,列出关系式即可.
【详解】
解:∵单价为 60元时,每星期卖出 100 个.销售单价,每涨价1元,少卖出 2个,
∴设销售单价为 x元,则涨价(x-60)元,每星期少卖出2(x-60)个.,
∴y=100 2(x-60)=-2x+220,
故选 C.
【点睛】
此题主要考查了由实际问题列函数关系式,关键是正确理解题意,找出题目中的等量关系.
二、填空题
1、 y 3x 4##
【分析】
先求出点 A、B的坐标,过点 A作 AF⊥AB,交直线 BC于点 F,过点 F作 EF⊥x轴,垂足为 E,然后由
全等三角形的判定和性质,等腰直角三角形的性质,求出点F的坐标,再利用待定系数法,即可求出
答案.
【详解】
解:∵一次函数 y=-2x+4的图像与 x轴、y轴分别交于点 A、B两点,
∴令 x 0,则 y 4;令 y 0,则 x 2,
∴点 A为(2,0),点 B为(0,4),
∴OA 2,OB 4;
过点 A作 AF⊥AB,交直线 BC于点 F,过点 F作 EF⊥x轴,垂足为 E,如图,
∴ AEF AOB 90 ,
∴ FAE BAE 90 ABO BAE,
∴ FAE ABO,
∵ ABE 45 ,
∴△ABF是等腰直角三角形,
∴AF=AB,
∴△ABO≌△FAE(AAS),
∴AO=FE,BO=AE,
∴FE 2, AE 4,
∴OE 4 2 2,
∴点 F的坐标为( 2, 2);
设直线 BC为 y ax b,则
2a b 2 a 3
,解得: ,
b 4 b 4
∴直线 BC的函数表达式为 y 3x 4;
故答案为: y 3x 4;
【点睛】
本题考查了一次函数的性质,全等三角形的判定和性质,等腰三角形的判定和性质,以及旋转的性
质,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行解题.
2、m>1
【分析】
由一次函数的性质可得 m-1 为正,从而可求得 m的取值范围.
【详解】
由题意知,m-1>0
则 m>1
故答案为:m>1
【点睛】
本题考查了一次函数的图象与性质,熟悉一次函数的图象与性质是关键.
3、2或-2
【分析】
4
由函数解析式确定与 x轴的交点坐标为 ( ,0),与 y轴的交点坐标为(0,4),然后根据函数图象与
k
坐标轴的面积为 4列出方程求解即可.
【详解】
解:∵在 y kx 4(k 0)中,
当 x 0时, y 4;
4
当 y 0时, x ,
k
4
∴ y kx 4的图象与 x轴的交点坐标为( ,0),与 y轴的交点坐标为(0,4),
k
1 4
由题意可得: 4 4,
2 k
解得: k 2.
故答案为:2或-2.
【点睛】
题目主要考查一次函数解析式的确定及其与坐标轴围成面积的计算方法,理解题意,得出方程是解题
关键.
4、x≤1
【分析】
由表格得到函数的增减性后,再得出 y 1时,对应的 x的值即可.
【详解】
解:当 x 1时, y 1,
根据表可以知道函数值 y随 x的增大而减小,
∴不等式 kx b 1的解集是 x 1.
故答案为: x 1.
【点睛】
此题考查了一次函数与一元一次不等式,认真体会一次函数与一元一次方程及一元一次不等式之间的
内在联系,理解一次函数的增减性是解决本题的关键.
5、8
【分析】
8
根据一次函数解析式可得: A ,0 ,B 0,8 ,过点 B作MN∥x轴,过点 A作 AM MN,过点 Q作
k
QN MN,由旋转的性质可得 AB BQ, ABQ 90 ,依据全等三角形的判定定理及性质可得:
,MA NB,NQ MB,即可确定点 Q的坐标,然后利用勾股定理得出 OQ的长
度,最后考虑在什么情况下取得最小值即可.
【详解】
8
解:函数 y
kx 8得: A ,0 ,B 0,8 ,过点 B作MN∥x轴,过点 A作 AM MN,过点 Q作
k
QN MN,连接 OQ,如图所示:
将线段 BA绕点 B逆时针旋转90 得到线段 BQ,
∴ AB BQ, ABQ 90 ,
∴ ABM MAB 90 , MBA NBQ 90 ,
∴ MAB NBQ,
在 与 中,
BMA QNB
MAB NBQ,
AB BQ
∴ ,
8
∴MA NB 8,NQ MB ,
k
8
点 Q的坐标为 8,8 ,
k
8 2
∴OQ 82 8
k
当 k 1或 k 1时,OQ取得最小值为 8,
故答案为:8.
【点睛】
题目主要考查一次函数与几何的综合问题,包括与坐标轴的交点,旋转,全等三角形的判定和性质,
勾股定理等,理解题意,作出相应图形是解题关键.
三、解答题
1、
(1)甲种货车一次原装8吨水泥,乙种货车一次能装10 吨水泥
(2) = 50 + 3600
(3)租用甲货 5辆,租用乙货车 4辆时,费用最少,为3850 元
【分析】
(1)设甲种货车一次原装 吨水泥,乙种货车一次能装 吨水泥,依题意列出二元一次方程组,故
可求解;
(2)根据甲种货车有 辆,则乙种货年有 (9 a)辆,即可列出函数关系;
(3)先根据题意求出 a的取值,再根据一次函数的性质即可求解.
(1)
解:设甲种货车一次原装 吨水泥,乙种货车一次能装 吨水泥,由题意得,
{2 + 3 = 46 x 8,解得 ,
+ 2 = 28 y 10
∴设甲种货车一次原装8吨水泥,乙种货车一次能装10 吨水泥.
(2)
解:∵甲种货车有 辆,∴乙种货年有 (9 a)辆.
∴ = 450 + 400(9 )
= 50 + 3600
(3)
解:∵ { ≥ 5 ,9 ≥ 0
∴ 5 ≤ ≤ 9,
∵ = 50 + 3600,50> 0,
∴ 随 的增大而增大,
∴当 = 5时,
有
= 3850(元)
∴租用甲货 5辆,租用乙货车4辆时,费用最少,为3850 元.
【点睛】
此题主要考查方程组与函数的实际应用,解题的关键是根据题意找到数量关系列出方程与函数求解.
2、(1)0-10 分钟的函数解析式为 = 2 + 40,20-40 分钟的函数解析式为 = 1200;(2)杨老师
的教学设计能实现,理由见解析
【分析】
= (1)设 0-10 分钟的函数解析式为 y kx b,20-40 分钟的函数解析式为 ,然后利用待定系数
法求解即可;
(2)将 = 48代入 = 2 + 40中得 = 4, = 48代入 = 1200中得 = 25,由此求解即可.
【详解】
解:(1)设 0-10 分钟的函数解析式为 y kx b,20-40 分钟的函数解析式为 = ,
{10 + = 60 ∴ = ,
60 = ,
40 20
{ = 2∴ = , = 1200, 40
∴0-10 分钟的函数解析式为 = 2 + 40,20-40 分钟的函数解析式为 = 1200;
(2)将 = 48代入 = 2 + 40中得 = 4,
将 = 48代入 = 1200中得 = 25,
∵25 4 = 21> 18,
∴杨老师的教学设计能实现.
【点睛】
本题主要考查了一次函数与反比例函数综合,解题的关键在于能够熟练掌握待定系数法求函数解析
式.
1
3、(1)C(﹣3,1),y= x+2;(2)见解析;(3)存在,点 N(﹣13,0)或(7,0)
3 3 3
【分析】
(1)过点 C作 CH⊥x轴于点 H,根据直线 y=2x+2 与 y轴,x轴分别交于 A,B两点,可得点 A、B的
坐标分别为:(0,2)、(﹣1,0),再证得△CHB≌△BOA,可得 BH=OA=2,CH=OB,即可求解;
(2)过点 C作 CH⊥x轴于点 H,DF⊥x轴于点 F,DG⊥y轴于点 G,可先证明△BCH≌△BDF,得到
BF=BH,再由 B(-1,0),C(﹣3,1),可得到 OF=OB=1,从而得到 DG=OB=1,进而证得
△BOE≌△DGE,即可求证;
(3)先求出直线 BC的表达式为 = 1 1,可得 k=3 ,再求出点 M(﹣6,0),从而得到 S
2 2 4 △
,S ,即可求解.
BMC △BPN
【详解】
解:(1)过点 C作 CH⊥x轴于点 H,
令 x=0,则 y=2,令 y=0,则 x=﹣2,则点 A、B的坐标分别为:(0,2)、(﹣1,0),
∵∠HCB+∠CBH=90°,∠CBH+∠ABO=90°,
∴∠ABO=∠BCH,
∵∠CHB=∠BOA=90°,BC=BA,
∴△CHB≌△BOA(AAS),
∴BH=OA=2,CH=OB,则点 C(﹣3,1),
设直线 AC的表达式为 y=mx+b( ≠ 0) ,
将点 A、C的坐标代入一次函数表达式:y=mx+b得:
{ = 2 { =
1
1 = 3 + ,解得: 3, = 2
1
故直线 AC的表达式为:y= x+2;
3
(2)如图,过点 C作 CH⊥x轴于点 H,DF⊥x轴于点 F,DG⊥y轴于点 G,
∵AC=AD,AB⊥CB,
∴BC=BD,
∵∠CBH=∠FBD,
∴△BCH≌△BDF,
∴BF=BH,
∵C(﹣3,1),
∴OH=3,
∵B(-1,0),
∴OB=1, BF=BH=2,
∴OF=OB=1,
∴DG=OB=1,
∵∠OEB=∠DEG,
∴△BOE≌△DGE,
∴BE=DE;
(3)设直线 BC的解析式为 = + ( ≠ 0) ,
1 1 1
把点 C(﹣3,1),B(﹣1,0),代入,得:
3 + = 1 = 1{ 1 1 + = 0 ,解得:{
1 2 ,
1
1 1 =
1 2
∴直线 BC的表达式为: = 1 1,
2 2
将点 P坐标代入直线 BC的表达式得:k=3 ,
4
1
∵直线 AC的表达式为:y= x+2,
3
∴点 M(﹣6,0),
∴S =1MB×y=1×5×1=5,
△BMC 2 C 2 2
∴S =1S =5=1NB×3=3NB,
△BPN 2 △BCM 4 2 4 8
解得:NB=10,
3
故点 N(﹣13,0)或(7,0).
3 3
【点睛】
本题主要考查了求一次函数解析式,等腰三角形的性质,一次函数的性质和图象,熟练掌握利用待定
系数法求一次函数解析式,等腰三角形的性质,一次函数的性质和图象是解题的关键.
4、(1)y=4x+8;(2)12
【分析】
(1)利用正比例函数的定义,设 y﹣2=k(2x+3),然后把已知的对应值代入求出 k得到 y与 x之间
的函数关系式;
(2)计算自变量为 1对应的 y的值即可.
【详解】
解:(1)设 y﹣2=k(2x+3),
把 x=1,y=12代入得 12﹣2=5k,解得 k=2,
所以 y﹣2=2(2x+3),
所以 y与 x之间的函数关系式为 y=4x+8;
(2)当 x=1时,y=4x+8=4+8=12.
【点睛】
本题考查了用待定系数法求反比例函数的解析式,解题关键是掌握正比例函数的定义条件:正比例函
数 y=kx 的定义条件是:k为常数且 k≠0.
5、(1)B(-6,0),C(2,0);(2)S=8-2t(0≤t<4),S=2t-8(t>4);(3)存在,F(4,
4)或 F(2,-2)
【分析】
(1)根据平方的非负性,求得 , ,即可求解;
(2)根据△OAC≌△OBE求得OE OC 2,分段讨论,分别求解即可;
(3)分两种情况讨论,当 在 的上方或 在 的下方,分别求解即可.
【详解】
解:(1)∵ 2 12 + 36+ ( 2)2 = 0
∴( 6)2 + ( 2)2 = 0∵( 6)2 ≥ 0,( 2)2 ≥ 0
∴m-6=0,n-2=0
∴m=6,n=2
∴B(-6,0),C(2,0)
(2)∵BD⊥AC,AO⊥BC ∠BDC=∠BDA=90°,∠AOB=∠AOC=90°
∴∠OAC+∠OCA=90°,∠OBE+∠OCA=90°
∴∠OAC=∠OBE
∴△OAC≌△OBE(AAS)
∴OC=OE=2
①当 0≤t<4时,BP=2t,PC=8-2t,S=1PC×OE=1(8-2t)×2=8-2t;
2 2
②当 t>4时,BP=2t,PC=2t-8,S=1PC×OE=1(2t-8)×2=2t-8;
2 2
(3)当 t=6时,BP=12
∴OB=OP=6
①当 F在 EP上方时,作 FM⊥y轴于 M,FN⊥x轴于 N
∴∠FME=∠FNP=90°
∵∠MFN=∠EFP=90°
∴∠MFE=∠NFP∵FE=FP
∴△ ≌△ ( )
∴ME=NP,FM=FN
∴MO=ON
∴2+EM=6-NP
∴ON=4
∴F(4,4)
②当 F在 EP下方时,作 FG⊥y轴于 G,FH⊥x轴于 H
∴∠FGE=∠FHP=90°
∵∠GFH=∠EFP=90°
∴∠GFE=∠HFP
∵FE=FP
∴△ ≌△ ( )
∴FG=FH, GE=HP
∴HF=OG,FG=OH
∴2+OG=6-OH
∴OG=OH=2
∴F(2,-2)
【点睛】
此题考查了坐标与图形,涉及了全等三角形的判定与性质,平分的性质,等腰三角形的性质,一次函
数的性质,解题的关键是掌握并灵活运用相关性质进行求解.
考试时间:90 分钟;命题人:数学教研组
考生注意:
1、本卷分第 I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100 分,考试时间90 分钟
2、答卷前,考生务必用0.5 毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新
的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第 I 卷(选择题 30 分)
一、单选题(10 小题,每小题 3分,共计 30 分)
1、如果函数 y=(2﹣k)x+5 是关于 x的一次函数,且 y随 x的值增大而减小,那么 k的取值范围是
( )
A.k≠0 B.k<2 C.k>2 D.k≠2
2、若点(-3,y )、(2,y )都在函数 y=-4x+b的图像上,则 y 与 y 的大小关系( )
1 2 1 2
A.y>y B.y<y C.y=y D.无法确定
1 2 1 2 1 2
3、自 2021 年 9月 16 日起,合肥市出租车价格调整,调整后的价格如图所示,根据图中的数据,下
列说法不正确的是( )
- 1 -
A.出租车的起步价为 10元 B.超过起步价以后,每公里加收2元
C.小明乘坐 2.8 公里收费为 10 元 D.小丽乘坐 10公里,收费 25 元
4、在平面直角坐标系中,已知点 A 1,2 ,点B 5,6 ,在 x轴上确定点 C,使得 ABC 的周长最小,
则点 C的坐标是( )
A. 4,0 B. 3,0 C. 2,0 D. 2.5,0
5、如图,直线 y kx b与 y mx n分别交 x轴于点 A 0.5,0 ,B 2,0 ,则不等式 kx b mx n 0
的解集为( ).
A. x 2 B.0 x 2 C. 0.5 x 2 D. x 0.5或 x 2
6、关于一次函数 y x 2 ,下列说法不正确的是( )
A.图象经过点(2,0) B.图象经过第三象限 C.函数 y随自变量 x的增大而减
小 D.当 x≥2时,y≤0
7、已知 k,b 为第四象限内的点,则一次函数 y kx b的图象大致是( )
A. B.
- 2 -
C. D.
8、若直线 y=kx+b经过一、二、四象限,则直线 y=bx﹣k的图象只能是图中的( )
A. B. C. D.
9、直线 y=﹣ax+a与直线 y=ax在同一坐标系中的大致图象可能是( )
A. B.
C. D.
10、某网店销售一款市场上畅销的护眼台灯,在销售过程中发现,这款护眼台灯销售单价为60 元
时,每星期卖出 100 个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销
售,设销售单价为 x元,每星期销售量为 y个.则 y与 x的函数关系式为( )
A.y=﹣2x+100 B.y=﹣2x+40 C.y=﹣2x+220 D.y=﹣2x+60
第Ⅱ卷(非选择题 70 分)
二、填空题(5小题,每小题 4分,共计 20 分)
- 3 -
1、如图,在平面直角坐标系中,一次函数 y=-2x+4 的图像与 x轴、y轴分别交于点 A、B,将直线
AB绕点 B顺时针旋转 45°,交 x轴于点 C,则直线 BC的函数表达式为_______.
2、一次函数 y=(m-1)x+2 的函数值 y随 x的增大而增大,则 m的取值范围是_____.
3、已知一次函数 y kx 4 k 0 的图象与两坐标轴围成的三角形面积为4,则 k ______.
4、一次函数 y=kx+b(k≠0)中两个变量 x、y的部分对应值如下表所示:
x … -2 -1 0 1 2 …
y … 8 5 2 -1 -4 …
那么关于 x的不等式 kx+b≥-1的解集是________.
5、若一次函数 y=kx+8(k≠0)的图象与 x轴、y轴分别交于 A、B两点,当 k的取值变化时,点 A
随之在 x轴上运动,将线段 AB绕点 B逆时针旋转90°得到 BQ,连接 OQ,则 OQ长的最小值是 ___.
三、解答题(5小题,每小题 10 分,共计 50 分)
1、成都市某在建地铁工程需要将一批水泥运送到施工现场,现有甲、乙两种货车可以租用.已知2
辆甲种货车和 3辆乙种货车一次可运送46吨水泥,1辆甲种货车和 2辆乙种货车一次可运送28 吨水
泥.
(1)求每辆甲种货车和每辆乙种货车一次分别能装运多少吨水泥?
(2)已知甲种货车每辆租金为450 元,乙种货车每辆租金为400 元,现租用甲、乙共9辆货车.请
求出租用货车的总费用W (元)与租用甲种货车的数量a (辆)之间的函数关系式.
(3)在(2)的条件下,为了保障能拉完这批水泥,发现甲种货车不少于5辆,请你为该企业设计如
何租车费用最少?并求出最少费用是多少元?
- 4 -
2、通过实验研究发现:初中生在体育课上运动能力指标(后简称指标)随上课时间的变化而变
化.上课开始时,学生随着运动,指标开始增加,中间一段时间,指标保持平稳状态,随后随着体力
的消耗,指标开始下降.指标 y随时间 x(分钟)变化的函数图象如图所示,当0 x 10和
10 x 20时,图象是线段;当20 x 40时,图象是反比例函数的一部分.
(1)求这个分段函数的表达式;
(2)杨老师想在一节课上进行某项运动的教学需要18 分钟,这项运动需要学生的运动能力指标不低
于 48 才能达到较好的效果,他的教学设计能实现吗?请说明理由.
3、如图 1,已知直线 y=2x+2 与 y轴,x轴分别交于 A,B两点,以 B为直角顶点在第二象限作等腰
Rt△ABC
(1)求点 C的坐标,并求出直线 AC的关系式;
(2)如图 2,直线 CB交 y轴于 E,在直线 CB上取一点 D,连接 AD,若 AD=AC,求证:BE=DE.
5
(3)如图 3,在(1)的条件下,直线 AC交 x轴于点 M,P(﹣ ,k)是线段 BC上一点,在 x轴上
2
是否存在一点 N,使△BPN面积等于△BCM面积的一半?若存在,请求出点 N的坐标;若不存在,请
说明理由.
- 5 -
4、若 y﹣2与 2x+3 成正比例,且当 x=1时,y=12.
(1)求 y与 x的函数解析式.
(2)求当 x=1时,函数 y的值.
5、如图,在平面直角坐标系中,点 A为 y轴正半轴上一点,点 B为 x轴负半轴上一点,点 C为 x轴
正半轴上一点,OA=OB=m,OC=n,满足 m2﹣12m+36+(n﹣2)2=0,作 BD⊥AC于 D,BD交 OA于
E.
(1)如图 1,求点 B、C的坐标;
(2)如图 2,动点 P从 B点出发,以每秒 2个单位的速度沿 x轴向右运动,设点 P运动的时间为 t,
△PEC的面积为 S,请用含 t的式子表示 S,并直接写出 t的取值范围;
(3)如图 3,在(2)的条件下,当 t=6时,在坐标平面内是否存在点 F,使△PEF是以 PE为底边
的等腰直角三角形,若存在,求出点 F的坐标,若不存在,请说明理由.
- 6 -
-参考答案-
一、单选题
1、C
【分析】
由题意 y 2 k x 5,y随x的增大而减小,可得自变量系数小于 0,进而可得 k 的范围.
【详解】
解:∵关于x的一次函数 y 2 k x 5的函数值 y随着 x的增大而减小,
2 k 0,
k 2.
故选 C.
【点睛】
本题主要考查了一次函数的增减性问题,解题的关键是:掌握在 y kx b中,k 0, y 随 x的增大而
增大,k 0, y随x的增大而减小.
2、A
【分析】
根据一次函数的性质得出 y随 x的增大而减小,进而求解.
【详解】
由一次函数 y=-4x+b可知,k=-4<0,y随x的增大而减小,
∵-3<2,
∴y>y,
1 2
故选:A.
【点睛】
本题考查一次函数的性质,熟知一次函数 y=kx+b(k≠0),当 k<0时,y随 x 的增大而减小是解题
的关键.
3、C
【分析】
根据(5,15),(7,19),确定函数的解析式,计算 y=10 时,x的值,结合生活实际,解答即可.
【详解】
设起步价以后函数的解析式为 y=kx+b,
5k b=15
把(5,15),(7,19)代入解析式,得 ,
7k+b 19
k 2
解得 ,
b 5
∴y=2x+5,
当 y=10 时,x=2.5,
当 x=10 时,y=25,
∴C错误,D正确,B正确,A正确,
故选 C.
【点睛】
本题考查了一次函数的实际应用,熟练掌握待定系数法,理解生活意义是解题的关键.
4、C
【分析】
因为 AB的长度是确定的,故△CAB的周长最小就是 CA+CB的值最小,作点 A关于 x轴的对称点 A′,
连接 A′B交 x轴于点 C,求出 C点坐标即可.
【详解】
解:如图,作点 A关于 x轴的对称点 A′,连接 A′B交 x轴于点 C,此时,AC+BC=A′C+BC=AC,长度
最小,
∵A(-1,2),
∴A′(-1,﹣2),
设直线 A′B的解析式为 y=kx+b(k≠0),把 A′(-1,﹣2),B 5,6 代入得,
5k b 6 k 2
∴ ,解得 ,
k b 2 b 4
∴直线 A′B的解析式为 y=-2x﹣4,
当 y=0时,x=-2,
∴C(-2,0).
故选:C
【点睛】
本题考查了轴对称-最短路径问题,一次函数与坐标轴交点问题,解题关键是确定点C的位置,利用
一次函数解析式求坐标.
5、C
【分析】
观察图象,可知当 x< - 0.5 时,y=kx+b>0,y=mx+n<0;当 - 0.5<x<2时,y=kx+b<0,y=mx+n<
0;当 x>2时,y=kx+b<0,y=mx+n>0,二者相乘为正的范围是本题的解集.
【详解】
解:由图象可得,
当 x>2时,(kx+b)<0,(mx+n)>0,则(kx+b)(mx+n)<0,故 A错误;
当 0<x<2时,kx+b<0,mx+n<0,(kx+b)(mx+n)>0,但是没有包含所有使得(kx+b)(mx+n)>
0的解集,故 B错误;
当 0.5 x 2时,kx+b<0,mx+n<0,故(kx+b)(mx+n)>0,且除此范围之外都不能使得(kx+b)
(mx+n)>0,故 C正确;
当 x<- 0.5 时,y=kx+b>0,y=mx+n<0;当 x>2时,y=kx+b<0,y=mx+n>0,则(kx+b)(mx+n)
<0,故 D错误;
故选:C.
【点睛】
本题考查了利用函数图象来解一元一次不等式,数形结合是解答本题的关键.
6、B
【分析】
当 y 0 时, x 2 ,可得图象经过点(2,0);再由 1 0,2 0 ,可得图象经过第一、二、四象限;
函数 y随自变量 x的增大而减小;然后根据 x 2 时, y 0 ,可得当 x≥2时,y≤0,即可求解.
【详解】
解:当 y 0 时, x 2 ,
∴图象经过点(2,0),故 A正确,不符合题意;
∵ 1 0,2 0 ,
∴图象经过第一、二、四象限,故B错误,符合题意;
∴函数 y随自变量 x的增大而减小,故C正确,不符合题意;
当 x 2 时, y 0 ,
∴当 x≥2时,y≤0,故 D正确,不符合题意;
故选:B
【点睛】
本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键.
7、A
【分析】
根据 k,b 为第四象限内的点,可得k 0,b 0 ,从而得到 b 0 ,进而得到一次函数 y kx b的图
象经过第一、二、三象限,即可求解.
【详解】
解:∵ k,b 为第四象限内的点,
∴ k 0,b 0 ,
∴ b 0 ,
∴一次函数 y kx b的图象经过第一、二、三象限.
故选:A
【点睛】
本题主要考查了坐标与图形,一次函数的图象,熟练掌握一次函数y kx b k 0 ,当 k 0,b 0
时,一次函数图象经过第一、二、三象限;当k 0,b 0时,一次函数图象经过第一、三、四象限;
当 k 0,b 0时,一次函数图象经过第一、二、四象限;当k 0,b 0时,一次函数图象经过第二、
三、四象限是解题的关键.
8、B
【分析】
根据直线 y=kx+b经过一、二、四象限,可得 k<0,b>0,从而得到直线 y=bx﹣k过一、二、三
象限,即可求解.
【详解】
解:∵直线 y=kx+b经过一、二、四象限,
∴k<0,b>0,
∴﹣k>0,
∴直线 y=bx﹣k过一、二、三象限,
∴选项 B中图象符合题意.
故选:B
【点睛】
本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键.
9、D
【分析】
若 y=ax过第一、三象限,则 a>0,所以 y=-ax+a过第一、二、四象限,可对A、B进行判断;若
y=ax过第二、四象限,则 a<0,-a>0,,所以 y=-ax+a过第一、三、四象限,与 y轴的交点在 y轴
负半轴,则可对 C、D进行判断.
【详解】
解:A、y=ax过第一、三象限,则 a>0,所以 y=-ax+a过第一、二、四象限,所以A选项不符合题
意;
B、y=ax过第一、三象限,则 a>0,所以 y=-ax+a过第一、二、四象限,所以B选项不符合题意;
C、y=ax过第二、四象限,则 a<0,-a>0,所以 y=-ax+a过第一、三、四象限,与 y轴的交点在 y
轴负半轴,所以 C选项不符合题意;
D、y=ax过第二、四象限,则 a<0,-a>0,所以 y=-ax+a过第一、三、四象限,与 y轴的交点在 y
轴负半轴,所以 D选项符合题意;
故选 D.
【点睛】
本题考查了一次函数的图象:一次函数 y=kx+b(k≠0)的图象为一条直线,当 k>0,图象过第一、
三象限;当 k<0,图象过第二、四象限;直线与 y轴的交点坐标为(0,b).
10、C
【分析】
根据单价为 60 元时,每星期卖出100 个,每涨价 1元,每星期少卖出 2个,列出关系式即可.
【详解】
解:∵单价为 60元时,每星期卖出 100 个.销售单价,每涨价1元,少卖出 2个,
∴设销售单价为 x元,则涨价(x-60)元,每星期少卖出2(x-60)个.,
∴y=100 2(x-60)=-2x+220,
故选 C.
【点睛】
此题主要考查了由实际问题列函数关系式,关键是正确理解题意,找出题目中的等量关系.
二、填空题
1、 y 3x 4##
【分析】
先求出点 A、B的坐标,过点 A作 AF⊥AB,交直线 BC于点 F,过点 F作 EF⊥x轴,垂足为 E,然后由
全等三角形的判定和性质,等腰直角三角形的性质,求出点F的坐标,再利用待定系数法,即可求出
答案.
【详解】
解:∵一次函数 y=-2x+4的图像与 x轴、y轴分别交于点 A、B两点,
∴令 x 0,则 y 4;令 y 0,则 x 2,
∴点 A为(2,0),点 B为(0,4),
∴OA 2,OB 4;
过点 A作 AF⊥AB,交直线 BC于点 F,过点 F作 EF⊥x轴,垂足为 E,如图,
∴ AEF AOB 90 ,
∴ FAE BAE 90 ABO BAE,
∴ FAE ABO,
∵ ABE 45 ,
∴△ABF是等腰直角三角形,
∴AF=AB,
∴△ABO≌△FAE(AAS),
∴AO=FE,BO=AE,
∴FE 2, AE 4,
∴OE 4 2 2,
∴点 F的坐标为( 2, 2);
设直线 BC为 y ax b,则
2a b 2 a 3
,解得: ,
b 4 b 4
∴直线 BC的函数表达式为 y 3x 4;
故答案为: y 3x 4;
【点睛】
本题考查了一次函数的性质,全等三角形的判定和性质,等腰三角形的判定和性质,以及旋转的性
质,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行解题.
2、m>1
【分析】
由一次函数的性质可得 m-1 为正,从而可求得 m的取值范围.
【详解】
由题意知,m-1>0
则 m>1
故答案为:m>1
【点睛】
本题考查了一次函数的图象与性质,熟悉一次函数的图象与性质是关键.
3、2或-2
【分析】
4
由函数解析式确定与 x轴的交点坐标为 ( ,0),与 y轴的交点坐标为(0,4),然后根据函数图象与
k
坐标轴的面积为 4列出方程求解即可.
【详解】
解:∵在 y kx 4(k 0)中,
当 x 0时, y 4;
4
当 y 0时, x ,
k
4
∴ y kx 4的图象与 x轴的交点坐标为( ,0),与 y轴的交点坐标为(0,4),
k
1 4
由题意可得: 4 4,
2 k
解得: k 2.
故答案为:2或-2.
【点睛】
题目主要考查一次函数解析式的确定及其与坐标轴围成面积的计算方法,理解题意,得出方程是解题
关键.
4、x≤1
【分析】
由表格得到函数的增减性后,再得出 y 1时,对应的 x的值即可.
【详解】
解:当 x 1时, y 1,
根据表可以知道函数值 y随 x的增大而减小,
∴不等式 kx b 1的解集是 x 1.
故答案为: x 1.
【点睛】
此题考查了一次函数与一元一次不等式,认真体会一次函数与一元一次方程及一元一次不等式之间的
内在联系,理解一次函数的增减性是解决本题的关键.
5、8
【分析】
8
根据一次函数解析式可得: A ,0 ,B 0,8 ,过点 B作MN∥x轴,过点 A作 AM MN,过点 Q作
k
QN MN,由旋转的性质可得 AB BQ, ABQ 90 ,依据全等三角形的判定定理及性质可得:
,MA NB,NQ MB,即可确定点 Q的坐标,然后利用勾股定理得出 OQ的长
度,最后考虑在什么情况下取得最小值即可.
【详解】
8
解:函数 y
kx 8得: A ,0 ,B 0,8 ,过点 B作MN∥x轴,过点 A作 AM MN,过点 Q作
k
QN MN,连接 OQ,如图所示:
将线段 BA绕点 B逆时针旋转90 得到线段 BQ,
∴ AB BQ, ABQ 90 ,
∴ ABM MAB 90 , MBA NBQ 90 ,
∴ MAB NBQ,
在 与 中,
BMA QNB
MAB NBQ,
AB BQ
∴ ,
8
∴MA NB 8,NQ MB ,
k
8
点 Q的坐标为 8,8 ,
k
8 2
∴OQ 82 8
k
当 k 1或 k 1时,OQ取得最小值为 8,
故答案为:8.
【点睛】
题目主要考查一次函数与几何的综合问题,包括与坐标轴的交点,旋转,全等三角形的判定和性质,
勾股定理等,理解题意,作出相应图形是解题关键.
三、解答题
1、
(1)甲种货车一次原装8吨水泥,乙种货车一次能装10 吨水泥
(2) = 50 + 3600
(3)租用甲货 5辆,租用乙货车 4辆时,费用最少,为3850 元
【分析】
(1)设甲种货车一次原装 吨水泥,乙种货车一次能装 吨水泥,依题意列出二元一次方程组,故
可求解;
(2)根据甲种货车有 辆,则乙种货年有 (9 a)辆,即可列出函数关系;
(3)先根据题意求出 a的取值,再根据一次函数的性质即可求解.
(1)
解:设甲种货车一次原装 吨水泥,乙种货车一次能装 吨水泥,由题意得,
{2 + 3 = 46 x 8,解得 ,
+ 2 = 28 y 10
∴设甲种货车一次原装8吨水泥,乙种货车一次能装10 吨水泥.
(2)
解:∵甲种货车有 辆,∴乙种货年有 (9 a)辆.
∴ = 450 + 400(9 )
= 50 + 3600
(3)
解:∵ { ≥ 5 ,9 ≥ 0
∴ 5 ≤ ≤ 9,
∵ = 50 + 3600,50> 0,
∴ 随 的增大而增大,
∴当 = 5时,
有
= 3850(元)
∴租用甲货 5辆,租用乙货车4辆时,费用最少,为3850 元.
【点睛】
此题主要考查方程组与函数的实际应用,解题的关键是根据题意找到数量关系列出方程与函数求解.
2、(1)0-10 分钟的函数解析式为 = 2 + 40,20-40 分钟的函数解析式为 = 1200;(2)杨老师
的教学设计能实现,理由见解析
【分析】
= (1)设 0-10 分钟的函数解析式为 y kx b,20-40 分钟的函数解析式为 ,然后利用待定系数
法求解即可;
(2)将 = 48代入 = 2 + 40中得 = 4, = 48代入 = 1200中得 = 25,由此求解即可.
【详解】
解:(1)设 0-10 分钟的函数解析式为 y kx b,20-40 分钟的函数解析式为 = ,
{10 + = 60 ∴ = ,
60 = ,
40 20
{ = 2∴ = , = 1200, 40
∴0-10 分钟的函数解析式为 = 2 + 40,20-40 分钟的函数解析式为 = 1200;
(2)将 = 48代入 = 2 + 40中得 = 4,
将 = 48代入 = 1200中得 = 25,
∵25 4 = 21> 18,
∴杨老师的教学设计能实现.
【点睛】
本题主要考查了一次函数与反比例函数综合,解题的关键在于能够熟练掌握待定系数法求函数解析
式.
1
3、(1)C(﹣3,1),y= x+2;(2)见解析;(3)存在,点 N(﹣13,0)或(7,0)
3 3 3
【分析】
(1)过点 C作 CH⊥x轴于点 H,根据直线 y=2x+2 与 y轴,x轴分别交于 A,B两点,可得点 A、B的
坐标分别为:(0,2)、(﹣1,0),再证得△CHB≌△BOA,可得 BH=OA=2,CH=OB,即可求解;
(2)过点 C作 CH⊥x轴于点 H,DF⊥x轴于点 F,DG⊥y轴于点 G,可先证明△BCH≌△BDF,得到
BF=BH,再由 B(-1,0),C(﹣3,1),可得到 OF=OB=1,从而得到 DG=OB=1,进而证得
△BOE≌△DGE,即可求证;
(3)先求出直线 BC的表达式为 = 1 1,可得 k=3 ,再求出点 M(﹣6,0),从而得到 S
2 2 4 △
,S ,即可求解.
BMC △BPN
【详解】
解:(1)过点 C作 CH⊥x轴于点 H,
令 x=0,则 y=2,令 y=0,则 x=﹣2,则点 A、B的坐标分别为:(0,2)、(﹣1,0),
∵∠HCB+∠CBH=90°,∠CBH+∠ABO=90°,
∴∠ABO=∠BCH,
∵∠CHB=∠BOA=90°,BC=BA,
∴△CHB≌△BOA(AAS),
∴BH=OA=2,CH=OB,则点 C(﹣3,1),
设直线 AC的表达式为 y=mx+b( ≠ 0) ,
将点 A、C的坐标代入一次函数表达式:y=mx+b得:
{ = 2 { =
1
1 = 3 + ,解得: 3, = 2
1
故直线 AC的表达式为:y= x+2;
3
(2)如图,过点 C作 CH⊥x轴于点 H,DF⊥x轴于点 F,DG⊥y轴于点 G,
∵AC=AD,AB⊥CB,
∴BC=BD,
∵∠CBH=∠FBD,
∴△BCH≌△BDF,
∴BF=BH,
∵C(﹣3,1),
∴OH=3,
∵B(-1,0),
∴OB=1, BF=BH=2,
∴OF=OB=1,
∴DG=OB=1,
∵∠OEB=∠DEG,
∴△BOE≌△DGE,
∴BE=DE;
(3)设直线 BC的解析式为 = + ( ≠ 0) ,
1 1 1
把点 C(﹣3,1),B(﹣1,0),代入,得:
3 + = 1 = 1{ 1 1 + = 0 ,解得:{
1 2 ,
1
1 1 =
1 2
∴直线 BC的表达式为: = 1 1,
2 2
将点 P坐标代入直线 BC的表达式得:k=3 ,
4
1
∵直线 AC的表达式为:y= x+2,
3
∴点 M(﹣6,0),
∴S =1MB×y=1×5×1=5,
△BMC 2 C 2 2
∴S =1S =5=1NB×3=3NB,
△BPN 2 △BCM 4 2 4 8
解得:NB=10,
3
故点 N(﹣13,0)或(7,0).
3 3
【点睛】
本题主要考查了求一次函数解析式,等腰三角形的性质,一次函数的性质和图象,熟练掌握利用待定
系数法求一次函数解析式,等腰三角形的性质,一次函数的性质和图象是解题的关键.
4、(1)y=4x+8;(2)12
【分析】
(1)利用正比例函数的定义,设 y﹣2=k(2x+3),然后把已知的对应值代入求出 k得到 y与 x之间
的函数关系式;
(2)计算自变量为 1对应的 y的值即可.
【详解】
解:(1)设 y﹣2=k(2x+3),
把 x=1,y=12代入得 12﹣2=5k,解得 k=2,
所以 y﹣2=2(2x+3),
所以 y与 x之间的函数关系式为 y=4x+8;
(2)当 x=1时,y=4x+8=4+8=12.
【点睛】
本题考查了用待定系数法求反比例函数的解析式,解题关键是掌握正比例函数的定义条件:正比例函
数 y=kx 的定义条件是:k为常数且 k≠0.
5、(1)B(-6,0),C(2,0);(2)S=8-2t(0≤t<4),S=2t-8(t>4);(3)存在,F(4,
4)或 F(2,-2)
【分析】
(1)根据平方的非负性,求得 , ,即可求解;
(2)根据△OAC≌△OBE求得OE OC 2,分段讨论,分别求解即可;
(3)分两种情况讨论,当 在 的上方或 在 的下方,分别求解即可.
【详解】
解:(1)∵ 2 12 + 36+ ( 2)2 = 0
∴( 6)2 + ( 2)2 = 0∵( 6)2 ≥ 0,( 2)2 ≥ 0
∴m-6=0,n-2=0
∴m=6,n=2
∴B(-6,0),C(2,0)
(2)∵BD⊥AC,AO⊥BC ∠BDC=∠BDA=90°,∠AOB=∠AOC=90°
∴∠OAC+∠OCA=90°,∠OBE+∠OCA=90°
∴∠OAC=∠OBE
∴△OAC≌△OBE(AAS)
∴OC=OE=2
①当 0≤t<4时,BP=2t,PC=8-2t,S=1PC×OE=1(8-2t)×2=8-2t;
2 2
②当 t>4时,BP=2t,PC=2t-8,S=1PC×OE=1(2t-8)×2=2t-8;
2 2
(3)当 t=6时,BP=12
∴OB=OP=6
①当 F在 EP上方时,作 FM⊥y轴于 M,FN⊥x轴于 N
∴∠FME=∠FNP=90°
∵∠MFN=∠EFP=90°
∴∠MFE=∠NFP∵FE=FP
∴△ ≌△ ( )
∴ME=NP,FM=FN
∴MO=ON
∴2+EM=6-NP
∴ON=4
∴F(4,4)
②当 F在 EP下方时,作 FG⊥y轴于 G,FH⊥x轴于 H
∴∠FGE=∠FHP=90°
∵∠GFH=∠EFP=90°
∴∠GFE=∠HFP
∵FE=FP
∴△ ≌△ ( )
∴FG=FH, GE=HP
∴HF=OG,FG=OH
∴2+OG=6-OH
∴OG=OH=2
∴F(2,-2)
【点睛】
此题考查了坐标与图形,涉及了全等三角形的判定与性质,平分的性质,等腰三角形的性质,一次函
数的性质,解题的关键是掌握并灵活运用相关性质进行求解.
