2023年河南省普通高中学业水平考试(2019版新教材)数学仿真模拟卷(一)(2月)(Word版含答案)
文档属性
| 名称 | 2023年河南省普通高中学业水平考试(2019版新教材)数学仿真模拟卷(一)(2月)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-21 11:06:27 | ||
图片预览



文档简介
河南省普通高中学业水平考试(2019版新教材)
数学仿真模拟卷(一)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合A={x|x≥2},B={x|-1<x<3},则A∩B=( )
A.{x|x≥2} B.{x| x<2} C.{x|2≤x<3} D.{x|-1≤x<2}
2.不等式x2-4x<0的解集是( )
A.(0,4) B.(-4,0) C.(-∞,4) D.(-∞,0)∪(4,+∞)
3.已知指数函数y=ax(a>0,a≠1)的图象过点(2,4),则loga4=( )
A. B. C.2 D.4
4.半径为2 cm,圆心角为1 rad的扇形的面积为( )
A.π cm2 B.1 cm2 C.2π cm2 D.2 cm2
5.已知角α的终边上一点的坐标为(-4,a),且tan α=-2,则a的值为( )
A.2 B.-2 C.8 D.-8
6.幂函数 (0≤m≤3,m∈Z)的图象关于y轴对称,且在(0,+∞)上是增函数,则m的值为( )
A.0 B.2 C.3 D.2或3
7.已知复数z满足iz=i-2(i为虚数单位),则z的虚部为( )
A.2 B.-2 C.1 D.-1
8.已知函数,则f(x)=则f(f(-2))=( )
A.1 B.2 C.-1 D.-2
9.若a,b都是实数,则“>”是“log2a>log2b”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.在△ABC中,a,b,c分别为角A,B,C的对边,已知b=1,C=,△ABC的面积为2,则边长a=( )
A.4 B.4 C.5 D.5
11. 已知圆锥的底面半径为4,高为3,则该圆锥的侧面积为( )
A.16π B.20π C.36π D.40π
12.2021年东京奥运会某国家游泳队有男运动员48人,女运动员36人,世界反兴奋剂机构采用分层抽样的方法,从该国游泳运动员中抽出一个容量为28的样本进行尿样兴奋剂检查,其中女运动员应抽的人数为( )
A.12 B.14 C.16 D.18
13.已知cos(π+α)=-,则sin(α-2π)等于( )
A. B.± C.- D.
14.某市气象局预报说,明天甲地降雨概率是0.3,乙地降雨概率是0.4,若明天这两地是否降雨相互独立,则明天这两地中至少有一个地方降雨的概率是( )
A.0.28 B.0.48 C.0.58 D.0.68
15.下列函数中是奇函数,且最小正周期是π的函数是( )
A.y=cos|2x| B.y=|sin x| C.y=sin D.y=cos
16.向量a=(1,1),b=(-1,0),则a与b的夹角为( )
A. B. C. D.
二、填空题(本大题共7小题,每小题3分,共21分)
17.函数f(x)=的零点是________.
18.在△ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,则B=________.
19.已知函数f(x)=sin(2x+φ)(其中0<φ<)的图象经过P,则φ的值为______.
20.已知m,n是平面α外的两条直线,给出下列三个论断:
①m∥n;②m∥α;③n∥α,以其中两个为条件,余下的一个为结论,写出你认为正确的一个________.
21.若x>0,y>0,且+=1,则x+y的最小值是________.
22.在掷一个骰子的试验中,设事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A∪B发生的概率为________.
23.在△ABC中,sin A=,cos B=-,则cos(A-B)=________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.已知函数f(x)=ln(3+x)+ln(3-x).
(1)求函数y=f(x)的定义域;
(2)判断函数y=f(x)的奇偶性.
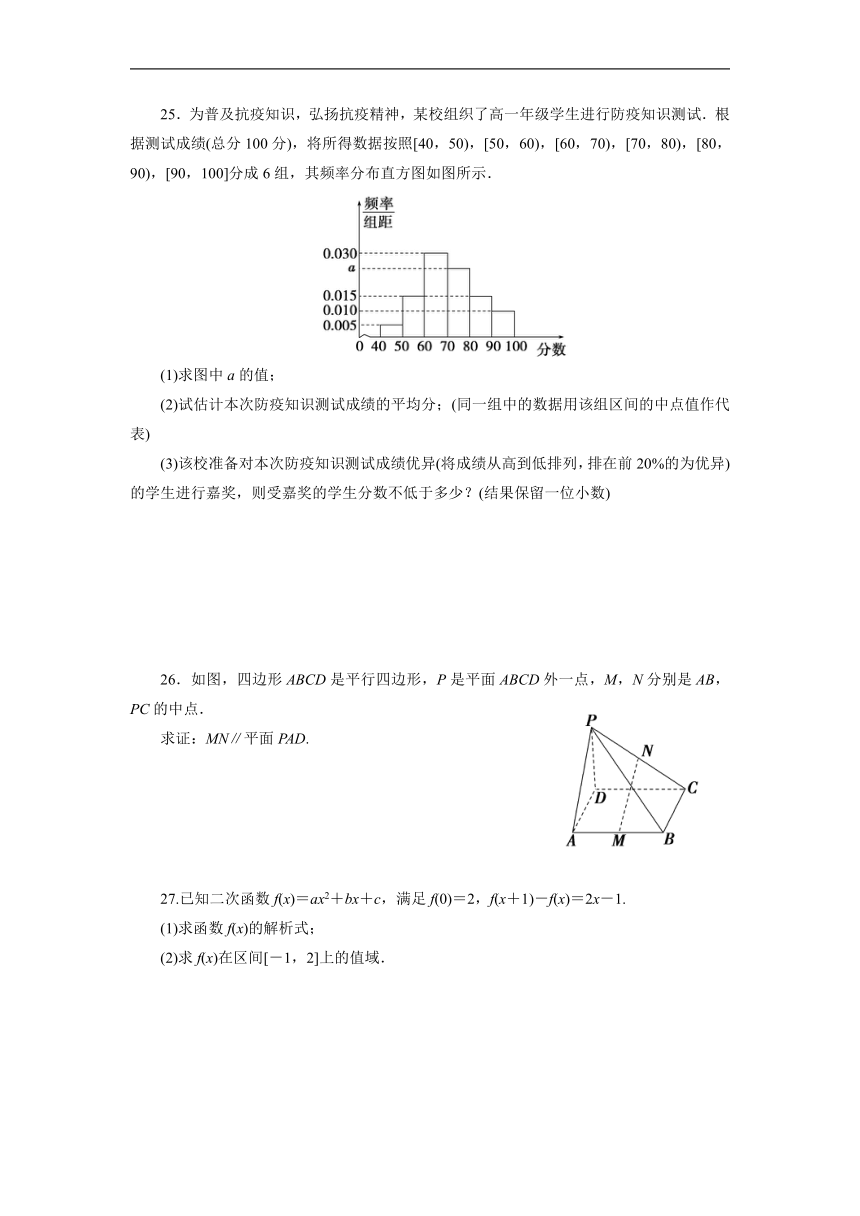
25.为普及抗疫知识,弘扬抗疫精神,某校组织了高一年级学生进行防疫知识测试.根据测试成绩(总分100分),将所得数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,其频率分布直方图如图所示.
(1)求图中a的值;
(2)试估计本次防疫知识测试成绩的平均分;(同一组中的数据用该组区间的中点值作代表)
(3)该校准备对本次防疫知识测试成绩优异(将成绩从高到低排列,排在前20%的为优异)的学生进行嘉奖,则受嘉奖的学生分数不低于多少?(结果保留一位小数)
26.如图,四边形ABCD是平行四边形,P是平面ABCD外一点,M,N分别是AB,PC的中点.
求证:MN∥平面PAD.
27.已知二次函数f(x)=ax2+bx+c,满足f(0)=2,f(x+1)-f(x)=2x-1.
(1)求函数f(x)的解析式;
(2)求f(x)在区间[-1,2]上的值域.
28.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 3月1日 3月2日 3月3日 3月4日 3月5日
温差x(℃) 10 11 13 12 8
发芽数y(颗) 23 25 30 26 16
(1)求这5天的平均发芽率;
(2)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,用(m,n)的形式列出所有的基本事件,并求满足“m,n∈[25,30]”的事件A的概率.
29.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数f(x)在上的值域.
仿真模拟卷(一)答案
1.解析:选C ∵A={x|x≥2},B={x|-1<x<3},
∴A∩B={x|x≥2}∩{x|-1<x<3}={x|2≤x<3}.
2.解析:选A 因为x2-4x<0,
则x(x-4)<0,0<x<4.
所以解集为x∈(0,4).
3.解析:选C 把点(2,4)代入y=ax(a>0,a≠1)得a2=4,解得a=2,所以loga4=log24=log222=2.
4.解析:选D ∵r=2 cm,α=1 rad,
∴扇形的面积为S=r2·α=×4×1=2 cm2.
5.解析:选C 因为角α的终边上一点的坐标为(-4,a),且tan α==-2,
所以解得a=8.
6.解析:选D 由题意,可得m2+m-2>0,且m2+m-2为偶数,
∵0≤m≤3,m∈Z,∴m=2或3.
7.解析:选A ∵iz=i-2,
∴z===1+2i,
∴z的虚部为2.
8.解析:选B 根据题意,函数f(x)=
则f(-2)=2-2=,
则f(f(-2))=f=log=log=2.
9.解析:选B 当a=1,b=0时,
>成立,但log2a>log2b不成立;
∵log2a>log2b,
∴a>b>0,
∴>,
故“>”是“log2a>log2b”的必要不充分条件.
10.解析:选A 已知b=1,C=,△ABC的面积为2,
利用S△ABC=absin C=2,解得a=4.
11.解析:选B ∵圆锥的底面半径r=4,高h=3,
∴母线l===5,
则该圆锥的侧面积为:
S侧=πrl=20π.
12.解析:选A 因为每个个体被抽到的概率等于=,
根据分层抽样方法的原理可得样本中女运动员的人数为36×=12.
13.解析:选B 因为cos(π+α)=-cos α=-,
所以cos α=,
则sin(α-2π)=sin α=±=±=±.
14.解析:选C 设事件A为明天甲地不降雨,事件B为明天乙地不降雨,
∴明天这两地中至少有一个地方降雨的概率
P=1-P(AB)=1-P(A)P(B)
=1-(1-0.3)(1-0.4)=0.58.
15.解析:选D 函数y=cos|2x|为偶函数,函数y=|sin x|为偶函数,函数y=sin=cos 2x为偶函数,函数y=cos=-sin 2x为奇函数,且周期为π.
16.解析:选C ∵a·b=-1,|a|=,|b|=1,
∴cos〈a,b〉==-,且〈a,b〉∈[0,π],
∴〈a,b〉=.
17.解析:令f(x)=0,即=0,即x-1=0或ln x=0,∴x=1,故函数f(x)的零点为1.
答案:1
18.解析:在△ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,
则cos B===,
又B∈(0,π),
所以B=.
答案:
19.解析:∵f(x)=sin(2x+φ)的图象经过P,
∴f=sin=cos φ=,
∴φ=±+2kπ,k∈Z,
又∵0<φ<,∴φ=.
答案:
20.解析:若m∥n,m∥α,则n∥α.同样,若m∥n,n∥α,则m∥α.
答案:①② ③(或①③ ②)
21.解析:∵x>0,y>0,+=1,
∴x+y=(x+y)·=1+++4
=5++≥5+2=5+4=9.
当且仅当=且+=1,
即时等号成立,即x+y的最小值为9.
答案:9
22.解析:∵在掷一个骰子的试验中,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,
∴P(A)==,P(B)==,
∴一次试验中事件A与事件B互斥,由概率加法公式,事件A∪B发生的概率为:
P(A∪B)=P(A)+P(B)=+=.
答案:
23.解析:因为cos B=-,且0所以所以sin B===,且0所以cos A===,
所以cos(A-B)=cos Acos B+sin Asin B,
=×+×=-.
答案:-
24.解:(1)要使函数有意义,则解得-3<x<3,故函数y=f(x)的定义域为(-3,3).
(2)由(1)可知,函数y=f(x)的定义域为(-3,3),关于原点对称.
对任意x∈(-3,3),则-x∈(-3,3).
∵f(-x)=ln(3-x)+ln(3+x)=f(x),
∴由函数奇偶性可知,函数y=f(x)为偶函数.
25.解:(1)由(0.005+0.010+0.015×2+a+0.030)×10=1,解得a=0.025,
(2)45×0.05+55×0.15+65×0.3+75×0.25+85×0.15+95×0.1=71,故本次防疫知识测试成绩的平均分为71,
(3)设受嘉奖的学生分数不低于x分,因为[80,90),[90,100]对应的频率分别为0.15,0.1,
所以(90-x)×0.015=0.1,解得x=≈83.3.
故受嘉奖的学生分数不低于83.3分.
26.证明:如图,取PD的中点G,连接GA,GN.
∵G,N分别是△PDC的边PD,PC的中点,
∴GN∥DC,GN=DC.
∵M为平行四边形ABCD的边AB的中点,
∴AM=DC,AM∥DC,
∴AM∥GN,AM=GN,
∴四边形AMNG为平行四边形,
∴MN∥AG.
又∵MN 平面PAD,AG 平面PAD,
∴MN∥平面PAD.
27.解:(1)由题意得f(0)=c=2,
f(x+1)-f(x)=a(x+1)2+b(x+1)+c-ax2-bx-c=2x-1,
整理得2ax+a+b=2x-1,
所以2a=2,a+b=-1,
所以a=1,b=-2,c=2,
所以f(x)=x2-2x+2.
(2)由(1)可得因为抛物线的开口向上,对称轴x=1,
故函数在[-1,2]上先减后增,
故当x=1时,函数取得最小值1,当x=-1时,函数取得最大值5,
所以函数f(x)在区间[-1,2]上的值域为[1,5].
28.解:(1)这5天的平均发芽率为:
(23+25+30+26+16)××100%=24%.
(2)从3月1日至3月5日任中选2天,
记发芽的种子数分别为m,n,
用(m,n)的形式列出所有的基本事件有10个,分别为:(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),(30,26),(30,16),(26,16).
满足“m,n∈[25,30]”的事件A包含的基本事件有:(25,30),(25,26),(30,26),共3个.
∴满足“m,n∈[25,30]”的事件A的概率P(A)=.
29.解:(1)根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象得A=2,
令函数f(x)的周期为T,则T=-=π,ω==2,
由f=0得:2×+φ=2kπ,
而|φ|<,于是得k=0,φ=.
所以函数f(x)的解析式是:
f(x)=2sin.
(2)由(1)知,当时x∈时,≤2x+≤,
则当2x+=,即x=时,f(x)max=2,
当2x+=,即x=,f(x)min=-,
所以函数f(x)在上的值域是[-,2].
数学仿真模拟卷(一)
一、选择题(本大题共16小题,每题3分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合A={x|x≥2},B={x|-1<x<3},则A∩B=( )
A.{x|x≥2} B.{x| x<2} C.{x|2≤x<3} D.{x|-1≤x<2}
2.不等式x2-4x<0的解集是( )
A.(0,4) B.(-4,0) C.(-∞,4) D.(-∞,0)∪(4,+∞)
3.已知指数函数y=ax(a>0,a≠1)的图象过点(2,4),则loga4=( )
A. B. C.2 D.4
4.半径为2 cm,圆心角为1 rad的扇形的面积为( )
A.π cm2 B.1 cm2 C.2π cm2 D.2 cm2
5.已知角α的终边上一点的坐标为(-4,a),且tan α=-2,则a的值为( )
A.2 B.-2 C.8 D.-8
6.幂函数 (0≤m≤3,m∈Z)的图象关于y轴对称,且在(0,+∞)上是增函数,则m的值为( )
A.0 B.2 C.3 D.2或3
7.已知复数z满足iz=i-2(i为虚数单位),则z的虚部为( )
A.2 B.-2 C.1 D.-1
8.已知函数,则f(x)=则f(f(-2))=( )
A.1 B.2 C.-1 D.-2
9.若a,b都是实数,则“>”是“log2a>log2b”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.在△ABC中,a,b,c分别为角A,B,C的对边,已知b=1,C=,△ABC的面积为2,则边长a=( )
A.4 B.4 C.5 D.5
11. 已知圆锥的底面半径为4,高为3,则该圆锥的侧面积为( )
A.16π B.20π C.36π D.40π
12.2021年东京奥运会某国家游泳队有男运动员48人,女运动员36人,世界反兴奋剂机构采用分层抽样的方法,从该国游泳运动员中抽出一个容量为28的样本进行尿样兴奋剂检查,其中女运动员应抽的人数为( )
A.12 B.14 C.16 D.18
13.已知cos(π+α)=-,则sin(α-2π)等于( )
A. B.± C.- D.
14.某市气象局预报说,明天甲地降雨概率是0.3,乙地降雨概率是0.4,若明天这两地是否降雨相互独立,则明天这两地中至少有一个地方降雨的概率是( )
A.0.28 B.0.48 C.0.58 D.0.68
15.下列函数中是奇函数,且最小正周期是π的函数是( )
A.y=cos|2x| B.y=|sin x| C.y=sin D.y=cos
16.向量a=(1,1),b=(-1,0),则a与b的夹角为( )
A. B. C. D.
二、填空题(本大题共7小题,每小题3分,共21分)
17.函数f(x)=的零点是________.
18.在△ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,则B=________.
19.已知函数f(x)=sin(2x+φ)(其中0<φ<)的图象经过P,则φ的值为______.
20.已知m,n是平面α外的两条直线,给出下列三个论断:
①m∥n;②m∥α;③n∥α,以其中两个为条件,余下的一个为结论,写出你认为正确的一个________.
21.若x>0,y>0,且+=1,则x+y的最小值是________.
22.在掷一个骰子的试验中,设事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A∪B发生的概率为________.
23.在△ABC中,sin A=,cos B=-,则cos(A-B)=________.
三、解答题(本大题共6小题,共31分,解答应写出文字说明、证明过程或演算步骤)
24.已知函数f(x)=ln(3+x)+ln(3-x).
(1)求函数y=f(x)的定义域;
(2)判断函数y=f(x)的奇偶性.
25.为普及抗疫知识,弘扬抗疫精神,某校组织了高一年级学生进行防疫知识测试.根据测试成绩(总分100分),将所得数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,其频率分布直方图如图所示.
(1)求图中a的值;
(2)试估计本次防疫知识测试成绩的平均分;(同一组中的数据用该组区间的中点值作代表)
(3)该校准备对本次防疫知识测试成绩优异(将成绩从高到低排列,排在前20%的为优异)的学生进行嘉奖,则受嘉奖的学生分数不低于多少?(结果保留一位小数)
26.如图,四边形ABCD是平行四边形,P是平面ABCD外一点,M,N分别是AB,PC的中点.
求证:MN∥平面PAD.
27.已知二次函数f(x)=ax2+bx+c,满足f(0)=2,f(x+1)-f(x)=2x-1.
(1)求函数f(x)的解析式;
(2)求f(x)在区间[-1,2]上的值域.
28.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 3月1日 3月2日 3月3日 3月4日 3月5日
温差x(℃) 10 11 13 12 8
发芽数y(颗) 23 25 30 26 16
(1)求这5天的平均发芽率;
(2)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,用(m,n)的形式列出所有的基本事件,并求满足“m,n∈[25,30]”的事件A的概率.
29.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数f(x)在上的值域.
仿真模拟卷(一)答案
1.解析:选C ∵A={x|x≥2},B={x|-1<x<3},
∴A∩B={x|x≥2}∩{x|-1<x<3}={x|2≤x<3}.
2.解析:选A 因为x2-4x<0,
则x(x-4)<0,0<x<4.
所以解集为x∈(0,4).
3.解析:选C 把点(2,4)代入y=ax(a>0,a≠1)得a2=4,解得a=2,所以loga4=log24=log222=2.
4.解析:选D ∵r=2 cm,α=1 rad,
∴扇形的面积为S=r2·α=×4×1=2 cm2.
5.解析:选C 因为角α的终边上一点的坐标为(-4,a),且tan α==-2,
所以解得a=8.
6.解析:选D 由题意,可得m2+m-2>0,且m2+m-2为偶数,
∵0≤m≤3,m∈Z,∴m=2或3.
7.解析:选A ∵iz=i-2,
∴z===1+2i,
∴z的虚部为2.
8.解析:选B 根据题意,函数f(x)=
则f(-2)=2-2=,
则f(f(-2))=f=log=log=2.
9.解析:选B 当a=1,b=0时,
>成立,但log2a>log2b不成立;
∵log2a>log2b,
∴a>b>0,
∴>,
故“>”是“log2a>log2b”的必要不充分条件.
10.解析:选A 已知b=1,C=,△ABC的面积为2,
利用S△ABC=absin C=2,解得a=4.
11.解析:选B ∵圆锥的底面半径r=4,高h=3,
∴母线l===5,
则该圆锥的侧面积为:
S侧=πrl=20π.
12.解析:选A 因为每个个体被抽到的概率等于=,
根据分层抽样方法的原理可得样本中女运动员的人数为36×=12.
13.解析:选B 因为cos(π+α)=-cos α=-,
所以cos α=,
则sin(α-2π)=sin α=±=±=±.
14.解析:选C 设事件A为明天甲地不降雨,事件B为明天乙地不降雨,
∴明天这两地中至少有一个地方降雨的概率
P=1-P(AB)=1-P(A)P(B)
=1-(1-0.3)(1-0.4)=0.58.
15.解析:选D 函数y=cos|2x|为偶函数,函数y=|sin x|为偶函数,函数y=sin=cos 2x为偶函数,函数y=cos=-sin 2x为奇函数,且周期为π.
16.解析:选C ∵a·b=-1,|a|=,|b|=1,
∴cos〈a,b〉==-,且〈a,b〉∈[0,π],
∴〈a,b〉=.
17.解析:令f(x)=0,即=0,即x-1=0或ln x=0,∴x=1,故函数f(x)的零点为1.
答案:1
18.解析:在△ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,
则cos B===,
又B∈(0,π),
所以B=.
答案:
19.解析:∵f(x)=sin(2x+φ)的图象经过P,
∴f=sin=cos φ=,
∴φ=±+2kπ,k∈Z,
又∵0<φ<,∴φ=.
答案:
20.解析:若m∥n,m∥α,则n∥α.同样,若m∥n,n∥α,则m∥α.
答案:①② ③(或①③ ②)
21.解析:∵x>0,y>0,+=1,
∴x+y=(x+y)·=1+++4
=5++≥5+2=5+4=9.
当且仅当=且+=1,
即时等号成立,即x+y的最小值为9.
答案:9
22.解析:∵在掷一个骰子的试验中,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,
∴P(A)==,P(B)==,
∴一次试验中事件A与事件B互斥,由概率加法公式,事件A∪B发生的概率为:
P(A∪B)=P(A)+P(B)=+=.
答案:
23.解析:因为cos B=-,且0
所以cos(A-B)=cos Acos B+sin Asin B,
=×+×=-.
答案:-
24.解:(1)要使函数有意义,则解得-3<x<3,故函数y=f(x)的定义域为(-3,3).
(2)由(1)可知,函数y=f(x)的定义域为(-3,3),关于原点对称.
对任意x∈(-3,3),则-x∈(-3,3).
∵f(-x)=ln(3-x)+ln(3+x)=f(x),
∴由函数奇偶性可知,函数y=f(x)为偶函数.
25.解:(1)由(0.005+0.010+0.015×2+a+0.030)×10=1,解得a=0.025,
(2)45×0.05+55×0.15+65×0.3+75×0.25+85×0.15+95×0.1=71,故本次防疫知识测试成绩的平均分为71,
(3)设受嘉奖的学生分数不低于x分,因为[80,90),[90,100]对应的频率分别为0.15,0.1,
所以(90-x)×0.015=0.1,解得x=≈83.3.
故受嘉奖的学生分数不低于83.3分.
26.证明:如图,取PD的中点G,连接GA,GN.
∵G,N分别是△PDC的边PD,PC的中点,
∴GN∥DC,GN=DC.
∵M为平行四边形ABCD的边AB的中点,
∴AM=DC,AM∥DC,
∴AM∥GN,AM=GN,
∴四边形AMNG为平行四边形,
∴MN∥AG.
又∵MN 平面PAD,AG 平面PAD,
∴MN∥平面PAD.
27.解:(1)由题意得f(0)=c=2,
f(x+1)-f(x)=a(x+1)2+b(x+1)+c-ax2-bx-c=2x-1,
整理得2ax+a+b=2x-1,
所以2a=2,a+b=-1,
所以a=1,b=-2,c=2,
所以f(x)=x2-2x+2.
(2)由(1)可得因为抛物线的开口向上,对称轴x=1,
故函数在[-1,2]上先减后增,
故当x=1时,函数取得最小值1,当x=-1时,函数取得最大值5,
所以函数f(x)在区间[-1,2]上的值域为[1,5].
28.解:(1)这5天的平均发芽率为:
(23+25+30+26+16)××100%=24%.
(2)从3月1日至3月5日任中选2天,
记发芽的种子数分别为m,n,
用(m,n)的形式列出所有的基本事件有10个,分别为:(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),(30,26),(30,16),(26,16).
满足“m,n∈[25,30]”的事件A包含的基本事件有:(25,30),(25,26),(30,26),共3个.
∴满足“m,n∈[25,30]”的事件A的概率P(A)=.
29.解:(1)根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象得A=2,
令函数f(x)的周期为T,则T=-=π,ω==2,
由f=0得:2×+φ=2kπ,
而|φ|<,于是得k=0,φ=.
所以函数f(x)的解析式是:
f(x)=2sin.
(2)由(1)知,当时x∈时,≤2x+≤,
则当2x+=,即x=时,f(x)max=2,
当2x+=,即x=,f(x)min=-,
所以函数f(x)在上的值域是[-,2].
同课章节目录
