四川省成都市名校2022-2023学年高三下学期开学考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 四川省成都市名校2022-2023学年高三下学期开学考试数学(理)试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-21 12:41:53 | ||
图片预览




文档简介
成都市名校2022-2023学年高三下学期开学考试数学试题(理科)
一、选择题(共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合A={1,2,x,},,且,则x=( )
A.-1 B.1 C.-1或0 D.-1或0或1
2.设复数,其在复平面内的对应的点记为Z,则( ).
A.z的虚部为 B. C.Z在第四象限 D.
3.某国有企业响应国家关于进一步深化改革,加强内循环的号召,不断自主创新提升产业技术水平,同时积极调整企业旗下的甲、乙、丙、丁、戊等5种产品的结构比例,近年来取得了显著效果、据悉该企业2022年5种系列产品年总收入是2021年的2倍,其中5种系列产品的年收入构成比例如下图所示.则以下说法错误的是( )
A.2022年甲系列产品收入和2021年的一样多
B.2022年乙和丙系列产品收入之和比2021年的企业总收入还多
C.2022年丁系列产品收入是2021年丁系列产品收入的
D.2022年戊系列产品收入是2021年戊系列产品收入的2倍还多
4.“攒尖”是中国古代建筑中屋项的一种结构形式,依据其不同的形状特征分为圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑如图所示,某园林中的一种亭阁式建筑为六角攒尖,它的主要部分的轮廓可以近似看作为一个正六棱锥.设此正六棱锥的侧面等腰三角形的顶角为,则该正六棱锥的侧棱长a与其底面内切圆半径r的比为( )
A. B. C. D.
5.已知,,则在方向上的投影所对应向量的坐标为( )
A.(0,1) B.(-1,0) C.(0,-1) D.(0,1)
6.若,且,则=( )
A. B.2 C.3 D.
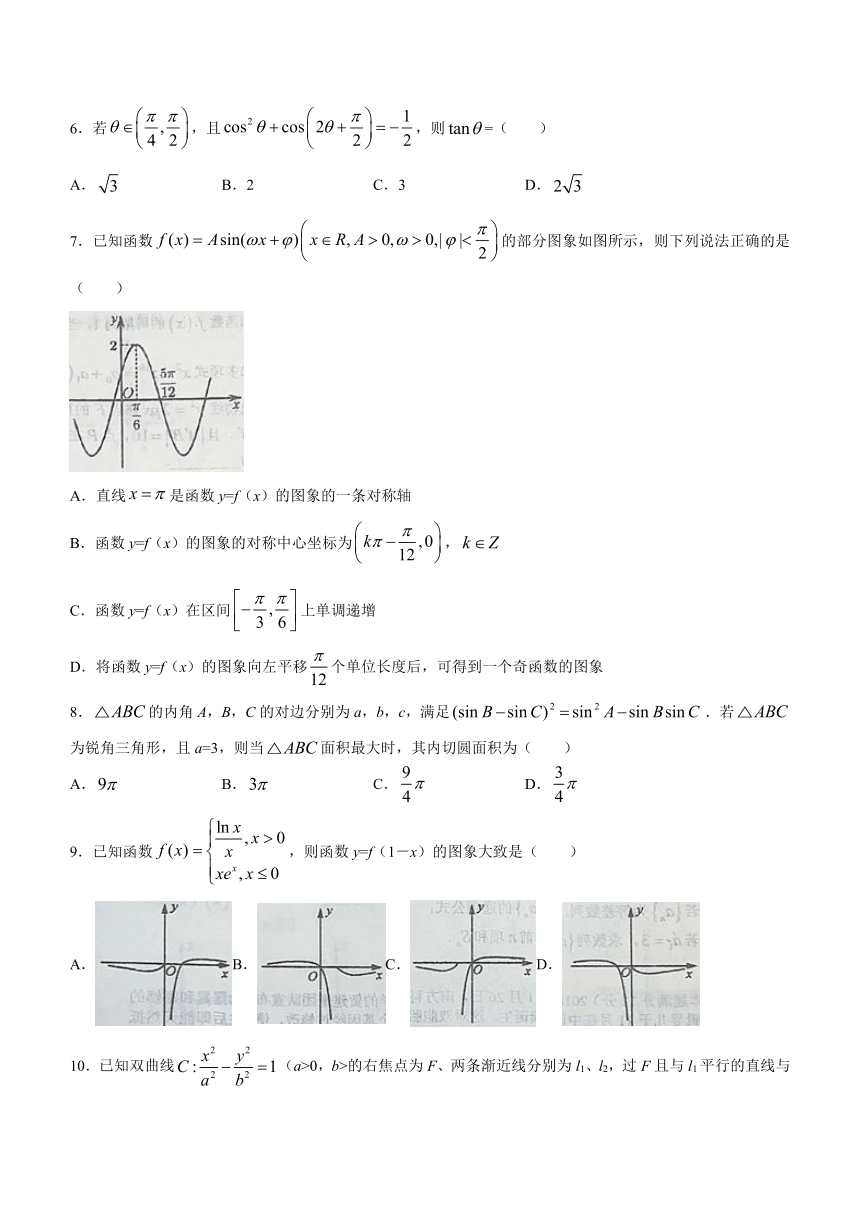
7.已知函数的部分图象如图所示,则下列说法正确的是( )
A.直线是函数y=f(x)的图象的一条对称轴
B.函数y=f(x)的图象的对称中心坐标为,
C.函数y=f(x)在区间上单调递增
D.将函数y=f(x)的图象向左平移个单位长度后,可得到一个奇函数的图象
8.的内角A,B,C的对边分别为a,b,c,满足.若为锐角三角形,且a=3,则当面积最大时,其内切圆面积为( )
A. B. C. D.
9.已知函数,则函数y=f(1-x)的图象大致是( )
A.B.C.D.
10.已知双曲线(a>0,b>的右焦点为F、两条渐近线分别为l1、l2,过F且与l1平行的直线与双曲线C及直线l2依次交于点B、D,点B恰好平分线段FD,则双曲线C的离心率为( )
A. B. C. D.2
11.已知,,,则a,b,c的大小关系为( )
A.a>b>c B.a>c>b C.b>a>c D.b>c>a
12.已知函数.则下列四个说法中正确的个数为( )
①曲线y=f(x)上存在三条互相平行的切线: ②函数y=f(x)有唯一极值点;
③函数y=f(x)有两个零点; ④过坐标原点O可作曲线y=f(x)的切线.
A.4 B.3 C.2 D.1
二、填空题:(共4小题,每小题5分,满分20分.)
13.已知函数f(x)的周期为1,当时,f(x)=-lnx,则的值为______.
14.已知多项式,则______.
15.过抛物线焦点的直线与抛物线交于A、B,点A、B在抛物线准线上的射影分别为、且,点在抛物线的准线上.若AP是的角平分线,则点到直线的距离为______.
16.如图,已知菱形ABCD边长为6,为对角线AC上一点,.将沿BD翻折到的位置,点移动到点,且二面角的大小为.
(1)三棱锥的外接球的半径为______.
(2)过作平面与该外接球相交,所得截面面积的最小值为______.
三、解答题(共6题,满分70分.)
17.(本题满分12分)已知数列中,对任意的,都有.
(I)若为等差数列,求的通项公式;
(II)若,求数列的前项和.
18.(本题满分12分)2018年11月26日,南方科技大学的贺建奎团队宣布一对名为露露和娜娜的基因编辑婴儿于11月在中国健康诞生。这对双胞胎的一个基因经过修改,使她们出生后即能天然抵抗艾滋病毒,这是世界上首例免疫艾滋病的基因编辑婴儿。当即全球有122位生物医学领域的科学家联名谴责,称“此项技术早就可以做”,但不做的原因是巨大的风险和道德伦理问题,直指这项所谓研究的生理医学伦理审查形同虚设,直接进行人体实验,只能用“疯狂”二字来形容。针对这件事,某部门就“基因编辑婴儿”的看法随机抽取了40人进行了问卷调查,其中男、女各20人,将问卷得分情况制作成茎叶图如下。为便于对调查对象作进一步研究分析,将得分高于85分的称为“A类”调查对象,得分不大于85分的称为“非A类”调查对象.
(I)某部门想要进一步了解“A类”调查对象的更多信息,将调查所得的频率视为概率.
①若从“A类”调查对象中抽取2人,求抽取的2人性别不同的概率P(A);
②若从“A类”调查对象中抽取3人,设被抽到的3人中男、女人数差的绝对值为X,求X的分布列与数学期望.
(II)通过问卷调查得到对应2×2列联表,请完成列联表中数据的填写,并说明是否能够在犯错误的概率不超过1%的前提下,认为调查对象是“A类”与性别有关?
“非A类”调查对象人数 “A类”调查对象人数 总计
男
女
总计
(参考公式与数据)
,
0.0508 0.010 0.001
3.841 6.635 10.828
19.(本题满分12分)如图,在几何体ABCDE中,面,,,.
(I)求证:平面平面DAE;
(Ⅱ)AB=1,,二面角的大小为,且,求AD的长.
20.(本题满分12分)已知椭圆E:,过原点O作直线l与椭圆E交于A、B两点,其中位于第一象限,为椭圆上异于A、B的一点.
(Ⅰ)若AC经过椭圆的右焦点,试求的最大值.
(II)若,记点,试证明B、C、D三点共线.
21.(本题满分12分)已知函数的图象在点处的切线方程为.
(I)用表示b、c;
(Ⅱ)若在上恒成立,求的取值范围;
(III) 证明: .
(选考题)请在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本题满分10分)在平面直角坐标系xOy中,直线l的参数方程为(为参数),
以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(I)求曲线的直角坐标方程;
(II)若直线与曲线交于M、N两点,求线段MN的长.
23.(本题满分10分)已知函数,.
(I)求函数f(x)的值域;
(Ⅱ)若a>0,b>0,且,不等式恒成立,求实数的取值范围.
成都市名校2022-2023学年高三下学期开学考试
数学试题(理科)参考答案
一、选择题:CBCAC CCDBB CB
二、填空题:13. 14.-120 15.5 16.(1) (2)
部分选填题参考解答
10.如图,由题意可知△ODF为等腰三角形,OD=DF,
则,代入渐近线方程,得,又,可得中点,
将其代入双曲线方程,可得,整理可得,∴.
11.联系函数不等式(当且仅当时取等)和(当且仅当时取等),
可得:(1);(2).
从而有.
12.,,,
(1)在,在,在,
则大致图象如图所示,可知方程可能有三个根,故①正确
(2)计算得,则存在,使得,
从而可知在,故②正确
(3)计算得,则,大致图象如图,故③正确
(4)设过原点的直线与相切于点,则有
,,,
消元整理可得,易知此方程无解,故④错误.综上,正确的是①②③.
(说明:由,也可以分析的零点个数)
14.由,可得.
15.(请同学们结合此题的学习与研究,进一步丰富对抛物线焦点弦的典型性质的认识与积累!)
【解法简介】过作的垂线,交准线于,连接,由,易证平分,则知M即已知中的点P.连接PB,已知PB平分,可推知,则P恰为的中点,故.
【性质积累】(1)可以证明,以焦点弦AB为直径的圆必与准线相切,且切点恰为的中点P;
(2)连接,可以证明恰好与此焦点弦AB相互垂直;
(3)连接,可以证明平分,平分,(图略)
16.(1)由题易知,均为等边三角形,取它们的中心M、N,过M、N分别作平面、平面的垂线,易知两垂线必交于一点,且点正是三棱锥的外接球球心.(如图所示)
记,则可知二面角的平面角为,在四边形中,可求得,则外接球半径;
(2)当截面面积取最小值时,可知截面,易求得,则截面圆半径,
故其面积.
三、解答题:
17.解:(I)由条件可得,,
因为为等差数列,记公差为,则有,
从而可解得,,则的通项公式为.
(II)法一:由,可得,两式相减可得:,
又由,则,所以,
故数列的奇数项构成以3为首项,4为公差的等差数列;
偶数项构成以1为首项,4为公差的等差数列.
所以,当为偶数时,
当为奇数时,.
综上,
法二:由及,可得,则,那么,
当为偶数时,;
当为奇数时,
综上,.
18.解:(I)①40人中符合“类”的调查对象共有16人,其中男性12人,女性4人,
从中抽取2人,则抽到性别不同的概率为.
(2)可能的取值为1,3,其中表示抽到2男1女或者2女1男,
则,
(注:也可同理直接计算)
故的分布列为
1 3
其期望
(II)由茎叶图可知,对应的列联表如下:
“非A类”调查对象人数 “A类”调查对象人数 总计
男 8 12 20
女 16 5 20
总计 24 16 40
由公式计算可得,
故能够在犯错误的概率不超过1%的前提下,认为调查对象是“A类”与性别有关.
19.解:(I)如图,取的中点M、N,,
连接、、,则知,且,
又,且,
所以,且,
则四边形为平行四边形,所以.
∵,M为的中点,∴,
∵平面,平面,∴.
又,∴平面
从而可得平面,由于平面,
所以平面平面,命题得证.
(II)由且,得,
又已知平面,,则有平面,
故可如图建立空间直角坐标系,
设,则有,,,,
所以,,记平面的一个法向量为,则有,不妨取,可得
而平面的一个法向量为,
则有,
由已知,则有,
即得,解之可得.
从而可得为所求.
20.解:(I)由经过椭圆的右焦点,设直线的方程为,
联立方程组,消去整理可得,
显然,且有,.
法一:则知,
(说明:此处也可借助椭圆的右焦点半径公式,得到求之)
而原点到直线的距离,
由于为线段的中点,则到直线的距离为,
则,其中,
由在上单调递增,故,
当,即时,等号成立,从而可知,的最大值为3.
法二:注意到为线段的中点,
则,
则有,以下同法一.
(1)当时,可知,则在上单调递减,
从而有,不合题意.
(2)当时,可进一步得到
①若,解得或,
当时,可知,则在上单调递增,
从而有,即有恒成立,符合题意;
当时,可知,则在上单调递减,则同理可知其不合题意;
②当,解得时,可知,
则在上单调递减,从而有,不合题意.
综上,的取值范围是.
(III)由(II)可知,当时,有,
令,则有,
且时,
设,则有
从而可得,,2,3,…n
将上述个不等式依次相加可得
即
从而可得成立.
22.解:(I)由题可得,即有,
结合转换公式,,代入整理,
经检验,曲线的直角坐标方程为.
(II)由已知易得,直线经过定点,且其倾斜角为,
由此其参数方程也可写为(为参数)(也称之为该直线的标准参数方程),
将其代入,整理可得,显然其,
设M、N两点对应的参数分别为、,则有,,
所以.
(说明:显然,此问也可直接解出参数值求之,或者用直线的普通方程与曲线联立求解之.)
23.解:(I)法一:由题得,
其中,当时,,从而易得函数的值域为.
法二:由绝对值不等式的性质可得,,
所以,当且仅当,即或时取得等号,
故函数的值域为.
(II)法一:由基本不等式,得,
当且仅当时取得等号,故的最小值为2.
法二:由柯西不等式,得,
当且仅当时取得等号,故的最小值为2.
由题得,,即,结合(I)之法一(零点分段,讨论求解)
等价于或或,由此可解得,
故原不等式的解集为.
一、选择题(共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合A={1,2,x,},,且,则x=( )
A.-1 B.1 C.-1或0 D.-1或0或1
2.设复数,其在复平面内的对应的点记为Z,则( ).
A.z的虚部为 B. C.Z在第四象限 D.
3.某国有企业响应国家关于进一步深化改革,加强内循环的号召,不断自主创新提升产业技术水平,同时积极调整企业旗下的甲、乙、丙、丁、戊等5种产品的结构比例,近年来取得了显著效果、据悉该企业2022年5种系列产品年总收入是2021年的2倍,其中5种系列产品的年收入构成比例如下图所示.则以下说法错误的是( )
A.2022年甲系列产品收入和2021年的一样多
B.2022年乙和丙系列产品收入之和比2021年的企业总收入还多
C.2022年丁系列产品收入是2021年丁系列产品收入的
D.2022年戊系列产品收入是2021年戊系列产品收入的2倍还多
4.“攒尖”是中国古代建筑中屋项的一种结构形式,依据其不同的形状特征分为圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑如图所示,某园林中的一种亭阁式建筑为六角攒尖,它的主要部分的轮廓可以近似看作为一个正六棱锥.设此正六棱锥的侧面等腰三角形的顶角为,则该正六棱锥的侧棱长a与其底面内切圆半径r的比为( )
A. B. C. D.
5.已知,,则在方向上的投影所对应向量的坐标为( )
A.(0,1) B.(-1,0) C.(0,-1) D.(0,1)
6.若,且,则=( )
A. B.2 C.3 D.
7.已知函数的部分图象如图所示,则下列说法正确的是( )
A.直线是函数y=f(x)的图象的一条对称轴
B.函数y=f(x)的图象的对称中心坐标为,
C.函数y=f(x)在区间上单调递增
D.将函数y=f(x)的图象向左平移个单位长度后,可得到一个奇函数的图象
8.的内角A,B,C的对边分别为a,b,c,满足.若为锐角三角形,且a=3,则当面积最大时,其内切圆面积为( )
A. B. C. D.
9.已知函数,则函数y=f(1-x)的图象大致是( )
A.B.C.D.
10.已知双曲线(a>0,b>的右焦点为F、两条渐近线分别为l1、l2,过F且与l1平行的直线与双曲线C及直线l2依次交于点B、D,点B恰好平分线段FD,则双曲线C的离心率为( )
A. B. C. D.2
11.已知,,,则a,b,c的大小关系为( )
A.a>b>c B.a>c>b C.b>a>c D.b>c>a
12.已知函数.则下列四个说法中正确的个数为( )
①曲线y=f(x)上存在三条互相平行的切线: ②函数y=f(x)有唯一极值点;
③函数y=f(x)有两个零点; ④过坐标原点O可作曲线y=f(x)的切线.
A.4 B.3 C.2 D.1
二、填空题:(共4小题,每小题5分,满分20分.)
13.已知函数f(x)的周期为1,当时,f(x)=-lnx,则的值为______.
14.已知多项式,则______.
15.过抛物线焦点的直线与抛物线交于A、B,点A、B在抛物线准线上的射影分别为、且,点在抛物线的准线上.若AP是的角平分线,则点到直线的距离为______.
16.如图,已知菱形ABCD边长为6,为对角线AC上一点,.将沿BD翻折到的位置,点移动到点,且二面角的大小为.
(1)三棱锥的外接球的半径为______.
(2)过作平面与该外接球相交,所得截面面积的最小值为______.
三、解答题(共6题,满分70分.)
17.(本题满分12分)已知数列中,对任意的,都有.
(I)若为等差数列,求的通项公式;
(II)若,求数列的前项和.
18.(本题满分12分)2018年11月26日,南方科技大学的贺建奎团队宣布一对名为露露和娜娜的基因编辑婴儿于11月在中国健康诞生。这对双胞胎的一个基因经过修改,使她们出生后即能天然抵抗艾滋病毒,这是世界上首例免疫艾滋病的基因编辑婴儿。当即全球有122位生物医学领域的科学家联名谴责,称“此项技术早就可以做”,但不做的原因是巨大的风险和道德伦理问题,直指这项所谓研究的生理医学伦理审查形同虚设,直接进行人体实验,只能用“疯狂”二字来形容。针对这件事,某部门就“基因编辑婴儿”的看法随机抽取了40人进行了问卷调查,其中男、女各20人,将问卷得分情况制作成茎叶图如下。为便于对调查对象作进一步研究分析,将得分高于85分的称为“A类”调查对象,得分不大于85分的称为“非A类”调查对象.
(I)某部门想要进一步了解“A类”调查对象的更多信息,将调查所得的频率视为概率.
①若从“A类”调查对象中抽取2人,求抽取的2人性别不同的概率P(A);
②若从“A类”调查对象中抽取3人,设被抽到的3人中男、女人数差的绝对值为X,求X的分布列与数学期望.
(II)通过问卷调查得到对应2×2列联表,请完成列联表中数据的填写,并说明是否能够在犯错误的概率不超过1%的前提下,认为调查对象是“A类”与性别有关?
“非A类”调查对象人数 “A类”调查对象人数 总计
男
女
总计
(参考公式与数据)
,
0.0508 0.010 0.001
3.841 6.635 10.828
19.(本题满分12分)如图,在几何体ABCDE中,面,,,.
(I)求证:平面平面DAE;
(Ⅱ)AB=1,,二面角的大小为,且,求AD的长.
20.(本题满分12分)已知椭圆E:,过原点O作直线l与椭圆E交于A、B两点,其中位于第一象限,为椭圆上异于A、B的一点.
(Ⅰ)若AC经过椭圆的右焦点,试求的最大值.
(II)若,记点,试证明B、C、D三点共线.
21.(本题满分12分)已知函数的图象在点处的切线方程为.
(I)用表示b、c;
(Ⅱ)若在上恒成立,求的取值范围;
(III) 证明: .
(选考题)请在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本题满分10分)在平面直角坐标系xOy中,直线l的参数方程为(为参数),
以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(I)求曲线的直角坐标方程;
(II)若直线与曲线交于M、N两点,求线段MN的长.
23.(本题满分10分)已知函数,.
(I)求函数f(x)的值域;
(Ⅱ)若a>0,b>0,且,不等式恒成立,求实数的取值范围.
成都市名校2022-2023学年高三下学期开学考试
数学试题(理科)参考答案
一、选择题:CBCAC CCDBB CB
二、填空题:13. 14.-120 15.5 16.(1) (2)
部分选填题参考解答
10.如图,由题意可知△ODF为等腰三角形,OD=DF,
则,代入渐近线方程,得,又,可得中点,
将其代入双曲线方程,可得,整理可得,∴.
11.联系函数不等式(当且仅当时取等)和(当且仅当时取等),
可得:(1);(2).
从而有.
12.,,,
(1)在,在,在,
则大致图象如图所示,可知方程可能有三个根,故①正确
(2)计算得,则存在,使得,
从而可知在,故②正确
(3)计算得,则,大致图象如图,故③正确
(4)设过原点的直线与相切于点,则有
,,,
消元整理可得,易知此方程无解,故④错误.综上,正确的是①②③.
(说明:由,也可以分析的零点个数)
14.由,可得.
15.(请同学们结合此题的学习与研究,进一步丰富对抛物线焦点弦的典型性质的认识与积累!)
【解法简介】过作的垂线,交准线于,连接,由,易证平分,则知M即已知中的点P.连接PB,已知PB平分,可推知,则P恰为的中点,故.
【性质积累】(1)可以证明,以焦点弦AB为直径的圆必与准线相切,且切点恰为的中点P;
(2)连接,可以证明恰好与此焦点弦AB相互垂直;
(3)连接,可以证明平分,平分,(图略)
16.(1)由题易知,均为等边三角形,取它们的中心M、N,过M、N分别作平面、平面的垂线,易知两垂线必交于一点,且点正是三棱锥的外接球球心.(如图所示)
记,则可知二面角的平面角为,在四边形中,可求得,则外接球半径;
(2)当截面面积取最小值时,可知截面,易求得,则截面圆半径,
故其面积.
三、解答题:
17.解:(I)由条件可得,,
因为为等差数列,记公差为,则有,
从而可解得,,则的通项公式为.
(II)法一:由,可得,两式相减可得:,
又由,则,所以,
故数列的奇数项构成以3为首项,4为公差的等差数列;
偶数项构成以1为首项,4为公差的等差数列.
所以,当为偶数时,
当为奇数时,.
综上,
法二:由及,可得,则,那么,
当为偶数时,;
当为奇数时,
综上,.
18.解:(I)①40人中符合“类”的调查对象共有16人,其中男性12人,女性4人,
从中抽取2人,则抽到性别不同的概率为.
(2)可能的取值为1,3,其中表示抽到2男1女或者2女1男,
则,
(注:也可同理直接计算)
故的分布列为
1 3
其期望
(II)由茎叶图可知,对应的列联表如下:
“非A类”调查对象人数 “A类”调查对象人数 总计
男 8 12 20
女 16 5 20
总计 24 16 40
由公式计算可得,
故能够在犯错误的概率不超过1%的前提下,认为调查对象是“A类”与性别有关.
19.解:(I)如图,取的中点M、N,,
连接、、,则知,且,
又,且,
所以,且,
则四边形为平行四边形,所以.
∵,M为的中点,∴,
∵平面,平面,∴.
又,∴平面
从而可得平面,由于平面,
所以平面平面,命题得证.
(II)由且,得,
又已知平面,,则有平面,
故可如图建立空间直角坐标系,
设,则有,,,,
所以,,记平面的一个法向量为,则有,不妨取,可得
而平面的一个法向量为,
则有,
由已知,则有,
即得,解之可得.
从而可得为所求.
20.解:(I)由经过椭圆的右焦点,设直线的方程为,
联立方程组,消去整理可得,
显然,且有,.
法一:则知,
(说明:此处也可借助椭圆的右焦点半径公式,得到求之)
而原点到直线的距离,
由于为线段的中点,则到直线的距离为,
则,其中,
由在上单调递增,故,
当,即时,等号成立,从而可知,的最大值为3.
法二:注意到为线段的中点,
则,
则有,以下同法一.
(1)当时,可知,则在上单调递减,
从而有,不合题意.
(2)当时,可进一步得到
①若,解得或,
当时,可知,则在上单调递增,
从而有,即有恒成立,符合题意;
当时,可知,则在上单调递减,则同理可知其不合题意;
②当,解得时,可知,
则在上单调递减,从而有,不合题意.
综上,的取值范围是.
(III)由(II)可知,当时,有,
令,则有,
且时,
设,则有
从而可得,,2,3,…n
将上述个不等式依次相加可得
即
从而可得成立.
22.解:(I)由题可得,即有,
结合转换公式,,代入整理,
经检验,曲线的直角坐标方程为.
(II)由已知易得,直线经过定点,且其倾斜角为,
由此其参数方程也可写为(为参数)(也称之为该直线的标准参数方程),
将其代入,整理可得,显然其,
设M、N两点对应的参数分别为、,则有,,
所以.
(说明:显然,此问也可直接解出参数值求之,或者用直线的普通方程与曲线联立求解之.)
23.解:(I)法一:由题得,
其中,当时,,从而易得函数的值域为.
法二:由绝对值不等式的性质可得,,
所以,当且仅当,即或时取得等号,
故函数的值域为.
(II)法一:由基本不等式,得,
当且仅当时取得等号,故的最小值为2.
法二:由柯西不等式,得,
当且仅当时取得等号,故的最小值为2.
由题得,,即,结合(I)之法一(零点分段,讨论求解)
等价于或或,由此可解得,
故原不等式的解集为.
同课章节目录
