中考直通车-存在性问题探究[下学期]
图片预览








文档简介
课件21张PPT。存在性开放问题石柱一职中 谭华勇目的存在性开放问题及解法 难点重点存在性开放问题及解法 通过对存在性开放问题的讲解,培养学生的综合理解能力和解决实际问题的能力
培养学生的思维能力和思考问题的全面性开放性问题从近几年的中考中主要可以归纳为: 条件开放性问题存在开放性问题结论开放性问题全开放性问题 存在性开放问题的基本特点: 在一定的条件下,判断某种数学结论存在的条件是否有,其一般形式为“已知条件A,B…,是否存在…,使…成立,若不能,请说明理由,若能,求出…”。 已知一次函数的图象经过第一、二、三象限,且与反比例函数的图象交于A、B两点,与y轴交于点C,与x轴交于点D,OB= ,tan∠DOB= 。
⑴求反比例函数的解析式;
⑵设点A的横坐标为m,△ABO的面积为S,求S与m的函数关系式,并写出自变量m的取值范围;
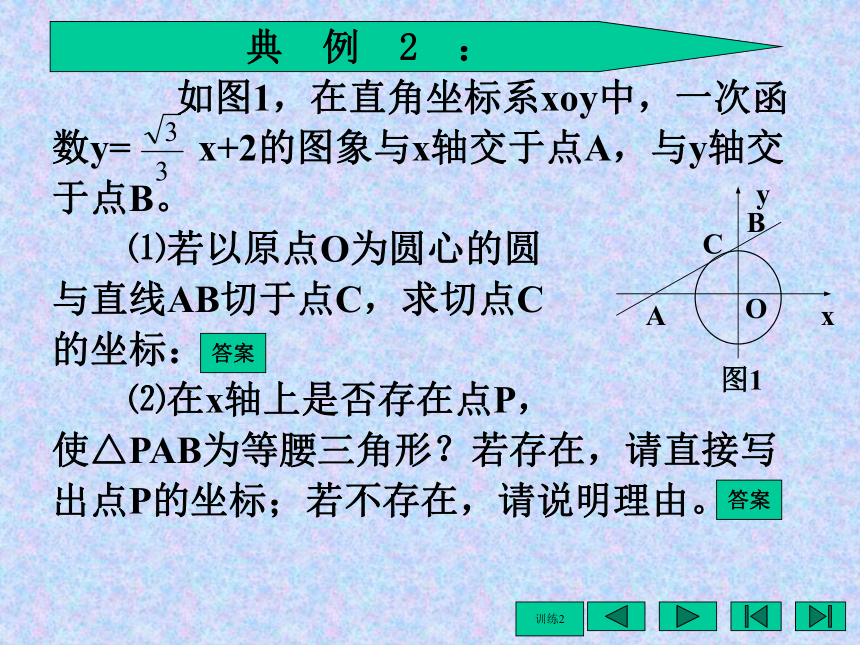
⑶当△ABO的面积等于 时,试判断过A、B两点的抛物线在x轴上截得的线段长能否等于3,如果能,求此抛物线的解析式;如果不能,请说明理由。课 前 引 例 :作业存在性开放问题的解题关键:对结论先作出肯定,再进行推理论证,若推理论证的结果是合理的(符合定理、公理、生活逻辑),则可肯定其存在;反之,则不存在。而这种存在性是不确定的,因而在解此类问题时,对题中所给条件下会产生的种种变化,在解题中应不重复不遗漏地加以研究和论证。 再见 是否存在这样的非负整数m,使关于x的一元二次方程m2x2-(2m-1)x+1=0有两个实数根。若存在,请求出m的值;若不存在,请说明理由。典 例 1 :训练1 如图1,在直角坐标系xoy中,一次函数y= x+2的图象与x轴交于点A,与y轴交于点B。 ⑴若以原点O为圆心的圆 与直线AB切于点C,求切点C 的坐标: ⑵在x轴上是否存在点P, 使△PAB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由。答案典 例 2 :答案训练2 如图2,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为 ,过C作⊙A的切线交x轴于点B。
⑴求切线BC的解析式;
⑵若点P是第一象限内⊙A上的一点,
过点P作⊙A的切线与直线BC相交于点
G,且∠CGP=120°,求点G的坐标。
⑶向左移动⊙A(圆心A始终保持在x轴上),
与直线BC交于E、F,在移动过程中是否存在点A,使△AEF是直角三角形?若存在,求出点A的坐标;若不存在,请说明理由。典 例 3 :答案答案答案训练3略解:⑴连结OC,过C作CG⊥OA于G,G典 例 2 答 案 :例2∴C(- , )易得OA= ,∠BAO=30°。 ∵OC=OAsin30°= ,OG=OCcos60°= ⑵直线y= x+2与x轴,y轴的交点坐标为
A(- ,0),B(0,2)。 假设点P存在,并设其坐标为P(x,0)那么AB可以为腰,也可以为底。即:以AB为底时,|PA|=|PB|。以AB为腰时,|PB|=|AB|以AB为腰时,|PA|=|AB|∴P点坐标为……典 例 2 答 案 :例3解:⑴连结AC典 例 3 答 案 : ,则易求C点的坐标为(0,2),B点的坐标为(-4,0),所以直线BC的解析式为y= x+2。典例3⑵过G点作x轴垂线,垂足为H,典 例 3 答 案 :连结AG,设G(x0,y0)。∵∠AGC=60°,AC= ,∴CG= 。H又OB=4,BC= 。由CO∥GH,得 ,则OH= 。即x0= 。又点G在直线BC上,故G( , )。∴y0= 。典例3典 例 3 答 案 :⑶如图4,在移动过程中,存在点A,使△AEF为直角三角形。若△AEF为直角三角形,
∵AE=AF,
∴△AEF为等腰三角形。∴∠AEF=∠AFE≠90°,故∠EAF=90°过A作AM⊥BC于M。在Rt△AEF中,∴易证△BOC∽△BMA,EF=∴典 例 3 答 案 :,OC=2而BC=可得AB=∴OA=4-∴A(-4+ ,0)当圆心A在点B的左侧时,设圆心为A′。过A′作A′M′⊥BC于M′。可得△A′M′B≌△AMB,∴OA′=OB+A′B=4+ ,即A′(-4- ,0)。故A(-4+ ,0)或(-4- ,0)所以A′B=AB=典例3变 式 训 练 1 :已知关于x的二次方程x2-2(m-2)x+m2=0。问是否存在实数m,使方程的两个实数根的平方和等于56,若存在,求出m的值;若不存在,请说明理由。例1已知一元二次方程-x2+bx+c=0有两个实数根是m,
4,其中0<m<4。
⑴求b、c的值(用含m的代数式表示);
⑵、设抛物线y=-x2+bx+c与x轴交于A、B两点,
与y轴交于点C,若点D的坐标为(0,-2),且
AD·BD=10,求抛物线的解析式及点C的坐标;
⑶、在⑵中所得的抛物线上是否存在一点P,使
得PC=PD?若存在,求出P点的坐标;若不存在,
请说明理由。变 式 训 练 2 :典例3如图5,已知直线MN与以AB为直径的半圆相
切于点C,∠A=28°。
⑴求∠ACM的度数;
⑵在MN上是否存在一
点D,使得AB·CD=AC·BC,
为什么?变 式 训 练 3 :课 堂 小 结存在性开放问题的解题关键2、如图6,梯形ABCD中,AD∥BC,
AB=CD=3cm,∠C=60°,BD⊥CD。
⑴求BC、AD的长度;
⑵若点P从B开始沿BC边
向点C以2cm/s的速度运动,点Q从点C开始沿CD边向点D以
1cm/s的速度运动,当P、Q分别从B、C同时出发时,写出五
边形ABPQD的面积S与运动时间t之间的函数关系式,并写出
自变量t的取值范围(不包含点P在B、C两点的情况);
⑶在⑵的前提下,是否存在某一时刻t,使线段PQ把梯形
ABCD分成两部分的面积比为1∶5?若存在求出t的值,若不
存在,请说明理由。作 业 与 思 考 :1、课前引入例题引例
培养学生的思维能力和思考问题的全面性开放性问题从近几年的中考中主要可以归纳为: 条件开放性问题存在开放性问题结论开放性问题全开放性问题 存在性开放问题的基本特点: 在一定的条件下,判断某种数学结论存在的条件是否有,其一般形式为“已知条件A,B…,是否存在…,使…成立,若不能,请说明理由,若能,求出…”。 已知一次函数的图象经过第一、二、三象限,且与反比例函数的图象交于A、B两点,与y轴交于点C,与x轴交于点D,OB= ,tan∠DOB= 。
⑴求反比例函数的解析式;
⑵设点A的横坐标为m,△ABO的面积为S,求S与m的函数关系式,并写出自变量m的取值范围;
⑶当△ABO的面积等于 时,试判断过A、B两点的抛物线在x轴上截得的线段长能否等于3,如果能,求此抛物线的解析式;如果不能,请说明理由。课 前 引 例 :作业存在性开放问题的解题关键:对结论先作出肯定,再进行推理论证,若推理论证的结果是合理的(符合定理、公理、生活逻辑),则可肯定其存在;反之,则不存在。而这种存在性是不确定的,因而在解此类问题时,对题中所给条件下会产生的种种变化,在解题中应不重复不遗漏地加以研究和论证。 再见 是否存在这样的非负整数m,使关于x的一元二次方程m2x2-(2m-1)x+1=0有两个实数根。若存在,请求出m的值;若不存在,请说明理由。典 例 1 :训练1 如图1,在直角坐标系xoy中,一次函数y= x+2的图象与x轴交于点A,与y轴交于点B。 ⑴若以原点O为圆心的圆 与直线AB切于点C,求切点C 的坐标: ⑵在x轴上是否存在点P, 使△PAB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由。答案典 例 2 :答案训练2 如图2,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为 ,过C作⊙A的切线交x轴于点B。
⑴求切线BC的解析式;
⑵若点P是第一象限内⊙A上的一点,
过点P作⊙A的切线与直线BC相交于点
G,且∠CGP=120°,求点G的坐标。
⑶向左移动⊙A(圆心A始终保持在x轴上),
与直线BC交于E、F,在移动过程中是否存在点A,使△AEF是直角三角形?若存在,求出点A的坐标;若不存在,请说明理由。典 例 3 :答案答案答案训练3略解:⑴连结OC,过C作CG⊥OA于G,G典 例 2 答 案 :例2∴C(- , )易得OA= ,∠BAO=30°。 ∵OC=OAsin30°= ,OG=OCcos60°= ⑵直线y= x+2与x轴,y轴的交点坐标为
A(- ,0),B(0,2)。 假设点P存在,并设其坐标为P(x,0)那么AB可以为腰,也可以为底。即:以AB为底时,|PA|=|PB|。以AB为腰时,|PB|=|AB|以AB为腰时,|PA|=|AB|∴P点坐标为……典 例 2 答 案 :例3解:⑴连结AC典 例 3 答 案 : ,则易求C点的坐标为(0,2),B点的坐标为(-4,0),所以直线BC的解析式为y= x+2。典例3⑵过G点作x轴垂线,垂足为H,典 例 3 答 案 :连结AG,设G(x0,y0)。∵∠AGC=60°,AC= ,∴CG= 。H又OB=4,BC= 。由CO∥GH,得 ,则OH= 。即x0= 。又点G在直线BC上,故G( , )。∴y0= 。典例3典 例 3 答 案 :⑶如图4,在移动过程中,存在点A,使△AEF为直角三角形。若△AEF为直角三角形,
∵AE=AF,
∴△AEF为等腰三角形。∴∠AEF=∠AFE≠90°,故∠EAF=90°过A作AM⊥BC于M。在Rt△AEF中,∴易证△BOC∽△BMA,EF=∴典 例 3 答 案 :,OC=2而BC=可得AB=∴OA=4-∴A(-4+ ,0)当圆心A在点B的左侧时,设圆心为A′。过A′作A′M′⊥BC于M′。可得△A′M′B≌△AMB,∴OA′=OB+A′B=4+ ,即A′(-4- ,0)。故A(-4+ ,0)或(-4- ,0)所以A′B=AB=典例3变 式 训 练 1 :已知关于x的二次方程x2-2(m-2)x+m2=0。问是否存在实数m,使方程的两个实数根的平方和等于56,若存在,求出m的值;若不存在,请说明理由。例1已知一元二次方程-x2+bx+c=0有两个实数根是m,
4,其中0<m<4。
⑴求b、c的值(用含m的代数式表示);
⑵、设抛物线y=-x2+bx+c与x轴交于A、B两点,
与y轴交于点C,若点D的坐标为(0,-2),且
AD·BD=10,求抛物线的解析式及点C的坐标;
⑶、在⑵中所得的抛物线上是否存在一点P,使
得PC=PD?若存在,求出P点的坐标;若不存在,
请说明理由。变 式 训 练 2 :典例3如图5,已知直线MN与以AB为直径的半圆相
切于点C,∠A=28°。
⑴求∠ACM的度数;
⑵在MN上是否存在一
点D,使得AB·CD=AC·BC,
为什么?变 式 训 练 3 :课 堂 小 结存在性开放问题的解题关键2、如图6,梯形ABCD中,AD∥BC,
AB=CD=3cm,∠C=60°,BD⊥CD。
⑴求BC、AD的长度;
⑵若点P从B开始沿BC边
向点C以2cm/s的速度运动,点Q从点C开始沿CD边向点D以
1cm/s的速度运动,当P、Q分别从B、C同时出发时,写出五
边形ABPQD的面积S与运动时间t之间的函数关系式,并写出
自变量t的取值范围(不包含点P在B、C两点的情况);
⑶在⑵的前提下,是否存在某一时刻t,使线段PQ把梯形
ABCD分成两部分的面积比为1∶5?若存在求出t的值,若不
存在,请说明理由。作 业 与 思 考 :1、课前引入例题引例
同课章节目录
