四川省成都市名校2022-2023学年高三下学期开学考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 四川省成都市名校2022-2023学年高三下学期开学考试数学(文)试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-21 12:58:52 | ||
图片预览




文档简介
成都市名校2022-2023学年高三下学期开学考试数学试题(文科)
一、选择题(共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合A={1,2,x,},,且,则x=( )
A.-1 B.1 C.-1或0 D.-1或0或1
2.设复数,其在复平面内的对应的点记为Z,则( ).
A.z的虚部为 B. C.Z在第四象限 D.
3.某国有企业响应国家关于进一步深化改革,加强内循环的号召,不断自主创新提升产业技术水平,同时积极调整企业旗下的甲、乙、丙、丁、戊等5种产品的结构比例,近年来取得了显著效果、据悉该企业2022年5种系列产品年总收入是2021年的2倍,其中5种系列产品的年收入构成比例如下图所示.则以下说法错误的是( )
A.2022年甲系列产品收入和2021年的一样多
B.2022年乙和丙系列产品收入之和比2021年的企业总收入还多
C.2022年丁系列产品收入是2021年丁系列产品收入的
D.2022年戊系列产品收入是2021年戊系列产品收入的2倍还多
4.“攒尖”是中国古代建筑中屋项的一种结构形式,依据其不同的形状特征分为圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑如图所示,某园林中的一种亭阁式建筑为六角攒尖,它的主要部分的轮廓可以近似看作为一个正六棱锥.设此正六棱锥的侧面等腰三角形的顶角为,则该正六棱锥的侧棱长a与其底面内切圆半径r的比为( )
A. B. C. D.
5.已知,,则在方向上的投影所对应向量的坐标为( )
A.(0,1) B.(-1,0) C.(0,-1) D.(0,1)
6.若,且,则=( )
A. B.2 C.3 D.
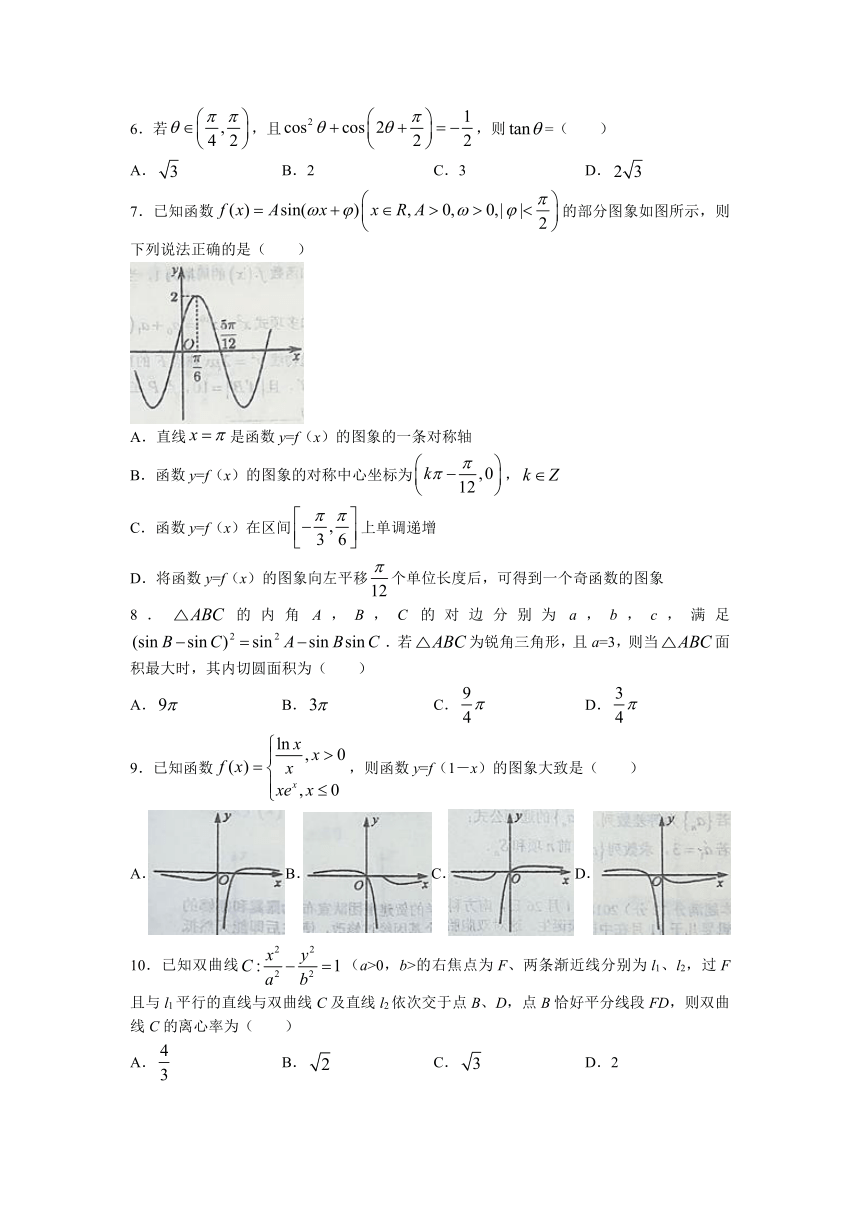
7.已知函数的部分图象如图所示,则下列说法正确的是( )
A.直线是函数y=f(x)的图象的一条对称轴
B.函数y=f(x)的图象的对称中心坐标为,
C.函数y=f(x)在区间上单调递增
D.将函数y=f(x)的图象向左平移个单位长度后,可得到一个奇函数的图象
8.的内角A,B,C的对边分别为a,b,c,满足.若为锐角三角形,且a=3,则当面积最大时,其内切圆面积为( )
A. B. C. D.
9.已知函数,则函数y=f(1-x)的图象大致是( )
A.B.C.D.
10.已知双曲线(a>0,b>的右焦点为F、两条渐近线分别为l1、l2,过F且与l1平行的直线与双曲线C及直线l2依次交于点B、D,点B恰好平分线段FD,则双曲线C的离心率为( )
A. B. C. D.2
11.已知,,,则a,b,c的大小关系为( )
A.a>b>c B.a>c>b C.b>a>c D.b>c>a
12.已知函数.则下列四个说法中正确的个数为( )
①曲线y=f(x)上存在三条互相平行的切线: ②函数y=f(x)有唯一极值点;
③函数y=f(x)有两个零点; ④过坐标原点O可作曲线y=f(x)的切线.
A.4 B.3 C.2 D.1
二、填空题:(共4小题,每小题5分,满分20分.)
13.已知函数f(x)的周期为1,当时,f(x)=-lnx,则的值为______.
14.若直线ax+y=0与2x+by—1=0平行,其中a、b均为正数,则a+2b的最小值为______.
15.过抛物线焦点的直线与抛物线交于A、B,点A、B在抛物线准线上的射影分别为、且,点在抛物线的准线上.若AP是的角平分线,则点到直线的距离为______.
16.如图,已知菱形ABCD边长为6,,E为对角线AC上一点,.将沿BD翻折到的位置,点移动到点,且二面角的大小为.
(1)三棱锥的外接球的半径为______.
(2)过作平面与该外接球相交,所得截面面积的最小值为______.
三、解答题(共6题,满分70分.)
17.(本题满分12分)已知公差为正数的等差数列的前n项和为,,______.
请从以下两个条件中任选一个,补充在题干的横线上,并解答下列问题:
①S2、S4、S8成等比数列;
②.
(I)求数列的通项公式;
(II)若,求数列的前n项和.
18.(本题满分12分)在花卉进行硬枝扦插过程中,常需要用生根粉调节植物根系生长。现有20株使用了生根粉的花卉样本,在对最终“花卉存活”和“花卉死亡”进行统计的同时,也对使用生根粉2个小时后的生根量进行了统计。这20株花卉生根量如下表所示,其中生根量在6根以下的视为“生根不足量”,大于或等于6根则视为“生根足量”.在这20株花卉样本中,“花卉存活”的有13株,而“花卉存活”但“生根不足量”的植株共1株.
编号 01 02 03 04 05 06 07 08 09 10 11 12 13 .14 15 16 17 18 18 20
生根量 6 8 3 8 9 5 6 6 2 7 7 5 9 6 7 8 8 4 6 9
(I)完成下面的2×2列联表,并判断是否能在犯错误概率不超过1%的前提下,认为“花卉存活”与“生根足量”有关?(参考公式与数据,见19题上方)
生根足量 生根不足量 总计
花卉存活
花卉死亡
总计 20
(II)若在该样本“生根不足量”的植株中随机抽取3株进行进一步检测,求这3株中恰有1株“花卉存活”的概率.
18题参考公式与数据:,
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.(本题满分12分)如图,在几何体ABCDE中,面,,,.
(I)求证:平面平面DAE;
(Ⅱ)AB=1,,,求CE与平面DAE所成角的正弦值.
20.(本题满分12分)已知函数,其中a∈R,设g(x)为f(x)的导函数.
(I)若a=1,求g(x)的最小值:
(II)若时,恒成立,求a的取值范围.
21.(本题满分12分)已知椭圆,过原点作直线与絠圆交于A、B两点,其中位于第一象限,为椭圆上异于A、B的一点.
(I)若AC经过椭圆的右焦点,试求的最大值.
(II)若,记点,试问:B、C、D三点是否共线?请给出判断并说明理由.
(选考题)请在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本题满分10分)在平面直角坐标系xOy中,直线l的参数方程为(为参数),
以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(I)求曲线的直角坐标方程;
(II)若直线与曲线交于M、N两点,求线段MN的长.
23.(本题满分10分)已知函数,.
(I)求函数f(x)的值域;
(Ⅱ)若a>0,b>0,且,不等式恒成立,求实数的取值范围.
成都市名校2022-2023学年高三下学期开学考试
数学试题(文科)参考答案
一、选择题:CBCA CCCDBB CB
二、填空题:13. 14.4 15.5 16.(1) (2)
部分选填题参考解答
10.如图,由题意可知△ODF为等腰三角形,OD=DF,
则,代入渐近线方程,得,又,可得中点,
将其代入双曲线方程,可得,整理可得,∴.
11.联系函数不等式(当且仅当时取等)和(当且仅当时取等),
可得:(1);(2).
从而有.
12.,,,
(1)在,在,在,
则大致图象如图所示,可知方程可能有三个根,故①正确
(2)计算得,则存在,使得,
从而可知在,故②正确
(3)计算得,则,大致图象如图,故③正确
(4)设过原点的直线与相切于点,则有
,,,
消元整理可得,易知此方程无解,故④错误.综上,正确的是①②③.
(说明:由,也可以分析的零点个数)
15.(请同学们结合此题的学习与研究,进一步丰富对抛物线焦点弦的典型性质的认识与积累!)
【解法简介】过作的垂线,交准线于,连接,由,易证平分,则知M即已知中的点P.连接PB,已知PB平分,可推知,则P恰为的中点,故.
【性质积累】(1)可以证明,以焦点弦AB为直径的圆必与准线相切,且切点恰为的中点P;
(2)连接,可以证明恰好与此焦点弦AB相互垂直;
(3)连接,可以证明平分,平分,(图略)
16.(1)由题易知,、均为等边三角形,取它们的中心M、N,过M、N分别作平面、平面的垂线,易知两垂线必交于一点,且点正是三棱锥的外接球球心.(如图所示)
记,则可知二面角的平面角为,在四边形中,可求得,则外接球半径;
(2)当截面面积取最小值时,可知截面,易求得,则截面圆半径,
故其面积.
三、解答题:
17.解:(I)选择①,设等差数列的公差为,则,
由题意可得,即有,解之得,
则.
选择②,设等差数列的公差为,则,
由可,得,解之得,
则.
(II)由(I)可得
所以.
18.解:(I)由题意及数据表可得,
“花卉存活”的有13株,“花卉死亡”的有7株;
“生根足量”的有15株,“生根不足量”的有5株.
①填写列联表:
生根足量 生根不足量 总计
花卉存活 12 1 13
花卉死亡 3 4 7
总计 15 5 20
②应用公式计算得:.
所以不能在犯错误概率不超过1%的前提下,认为“花卉存活”与“生根足量”有关.
(II)样本中“生根不足量”的有5株,其中“花卉死亡”的有4株,记为A,B,C,D;
“花卉存活”的有1株,记为a.设事件A:从5株中随机抽取3株中恰有1株存活,可知其包含的所有情况为:ABC,ABD,ACD,BCD;ABa,ACa,ADa,BCa,BDa,Ca.共10种,其中恰有1株“花卉存活”的情况为ABa,ACa,ADda,BCa,BDa,CDa.共6种.
故所求事件的概率为.
19.解:(I)如图,取的中点M、N,,
连接、、,则知,且,
又,且,
所以,且,
则四边形为平行四边形,所以.
∵,M为的中点,∴,
∵平面,平面,∴.
又,∴平面
从而可得平面,由于平面,
所以平面平面,命题得证.
(II)由(I)知,平面DAE于,则为CE与平面DAE所成角.且在Rt中,,由且,得,
又已知平面,平面,∴,
∵,∴平面ABCD
设,则,那么有,
则,解得,即有.
从而易得,在Rt中,;
又在Rt中,,则知;
∴,即CE与平面DAE所成角的正弦值为.
20.解:(I)时,由,可得,
则,那么有,所以在定义域上单调递增,
注意到,从而可得,,
即知在上单调递减,在上单调递增,
故,即当时,的最小值为0.
(II)由,可得,
由(I),同理可知,在上单调递增,则.讨论如下:
(1)当时,有,则在上单调递增,
从而有,符合题意.
(2)当时,有,由于在上单调递增,
且,所以,使得,
从而可知当时,,则在上单调递减,
此时有,不合题意.
综上,的取值范围为.
21.解:(I)由AC经过椭圆的右焦点,设直线AC的方程为,
联立方程组,消去整理可得,
显然,且有,.
法一:则知,
(说明:此处也可借助椭圆的右焦点半径公式,得到求之)
而原点到直线AC的距离,
由于为线段AB的中点,则到直线AC的距离为2d,
则,其中,
由在上单调递增,故,
当,即时,等号成立,从而可知,的最大值为3.
法二:注意到为线段AB的中点,则,
则有,以下同法一.
(II)B、C、D三点共线,证明如下:
法一:(证明点在直线BC上,即证点的坐标适合直线BC的方程)
一方面,由,两式相减整理可得,
另一方面,,从而可得为定值.
由,得,即有,又,
可得,从而直线BC的方程为,
令,可解得,
即点在直线BC上,故B、C、D三点共线.
法二:(通过坐标运算转化,证明)
由,得,即有,则
同法一,应用“点差法”得到,即有,
又由,,则,
∴,故B、C、D三点共线.
(说明:此问也可通过借助坐标运算证明,得到三点共线,具体方法过程略.)
22.解:(I)由题可得,即有,
结合转换公式,,
代入整理,
经检验,曲线的直角坐标方程为.
(II)由已知易得,直线经过定点,且其倾斜角为,
由此其参数方程也可写为(为参数)(也称之为该直线的标准参数方程),
将其代入,整理可得,显然其,
设M、N两点对应的参数分别为、,则有,,
所以.
(说明:显然,此问也可直接解出参数值求之,或者用直线的普通方程与曲线联立求解之.)
23.解:(I)法一:由题得,
其中,当时,,从而易得函数的值域为.
法二:由绝对值不等式的性质可得,,
所以,当且仅当,即或时取得等号,
故函数的值域为.
(II)法一:由基本不等式,得,
当且仅当时取得等号,故的最小值为2.
法二:由柯西不等式,得,
当且仅当时取得等号,故的最小值为2.
由题得,,即,结合(I)之法一(零点分段,讨论求解)
等价于或或,由此可解得,故原不等式的解集为.
一、选择题(共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合A={1,2,x,},,且,则x=( )
A.-1 B.1 C.-1或0 D.-1或0或1
2.设复数,其在复平面内的对应的点记为Z,则( ).
A.z的虚部为 B. C.Z在第四象限 D.
3.某国有企业响应国家关于进一步深化改革,加强内循环的号召,不断自主创新提升产业技术水平,同时积极调整企业旗下的甲、乙、丙、丁、戊等5种产品的结构比例,近年来取得了显著效果、据悉该企业2022年5种系列产品年总收入是2021年的2倍,其中5种系列产品的年收入构成比例如下图所示.则以下说法错误的是( )
A.2022年甲系列产品收入和2021年的一样多
B.2022年乙和丙系列产品收入之和比2021年的企业总收入还多
C.2022年丁系列产品收入是2021年丁系列产品收入的
D.2022年戊系列产品收入是2021年戊系列产品收入的2倍还多
4.“攒尖”是中国古代建筑中屋项的一种结构形式,依据其不同的形状特征分为圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑如图所示,某园林中的一种亭阁式建筑为六角攒尖,它的主要部分的轮廓可以近似看作为一个正六棱锥.设此正六棱锥的侧面等腰三角形的顶角为,则该正六棱锥的侧棱长a与其底面内切圆半径r的比为( )
A. B. C. D.
5.已知,,则在方向上的投影所对应向量的坐标为( )
A.(0,1) B.(-1,0) C.(0,-1) D.(0,1)
6.若,且,则=( )
A. B.2 C.3 D.
7.已知函数的部分图象如图所示,则下列说法正确的是( )
A.直线是函数y=f(x)的图象的一条对称轴
B.函数y=f(x)的图象的对称中心坐标为,
C.函数y=f(x)在区间上单调递增
D.将函数y=f(x)的图象向左平移个单位长度后,可得到一个奇函数的图象
8.的内角A,B,C的对边分别为a,b,c,满足.若为锐角三角形,且a=3,则当面积最大时,其内切圆面积为( )
A. B. C. D.
9.已知函数,则函数y=f(1-x)的图象大致是( )
A.B.C.D.
10.已知双曲线(a>0,b>的右焦点为F、两条渐近线分别为l1、l2,过F且与l1平行的直线与双曲线C及直线l2依次交于点B、D,点B恰好平分线段FD,则双曲线C的离心率为( )
A. B. C. D.2
11.已知,,,则a,b,c的大小关系为( )
A.a>b>c B.a>c>b C.b>a>c D.b>c>a
12.已知函数.则下列四个说法中正确的个数为( )
①曲线y=f(x)上存在三条互相平行的切线: ②函数y=f(x)有唯一极值点;
③函数y=f(x)有两个零点; ④过坐标原点O可作曲线y=f(x)的切线.
A.4 B.3 C.2 D.1
二、填空题:(共4小题,每小题5分,满分20分.)
13.已知函数f(x)的周期为1,当时,f(x)=-lnx,则的值为______.
14.若直线ax+y=0与2x+by—1=0平行,其中a、b均为正数,则a+2b的最小值为______.
15.过抛物线焦点的直线与抛物线交于A、B,点A、B在抛物线准线上的射影分别为、且,点在抛物线的准线上.若AP是的角平分线,则点到直线的距离为______.
16.如图,已知菱形ABCD边长为6,,E为对角线AC上一点,.将沿BD翻折到的位置,点移动到点,且二面角的大小为.
(1)三棱锥的外接球的半径为______.
(2)过作平面与该外接球相交,所得截面面积的最小值为______.
三、解答题(共6题,满分70分.)
17.(本题满分12分)已知公差为正数的等差数列的前n项和为,,______.
请从以下两个条件中任选一个,补充在题干的横线上,并解答下列问题:
①S2、S4、S8成等比数列;
②.
(I)求数列的通项公式;
(II)若,求数列的前n项和.
18.(本题满分12分)在花卉进行硬枝扦插过程中,常需要用生根粉调节植物根系生长。现有20株使用了生根粉的花卉样本,在对最终“花卉存活”和“花卉死亡”进行统计的同时,也对使用生根粉2个小时后的生根量进行了统计。这20株花卉生根量如下表所示,其中生根量在6根以下的视为“生根不足量”,大于或等于6根则视为“生根足量”.在这20株花卉样本中,“花卉存活”的有13株,而“花卉存活”但“生根不足量”的植株共1株.
编号 01 02 03 04 05 06 07 08 09 10 11 12 13 .14 15 16 17 18 18 20
生根量 6 8 3 8 9 5 6 6 2 7 7 5 9 6 7 8 8 4 6 9
(I)完成下面的2×2列联表,并判断是否能在犯错误概率不超过1%的前提下,认为“花卉存活”与“生根足量”有关?(参考公式与数据,见19题上方)
生根足量 生根不足量 总计
花卉存活
花卉死亡
总计 20
(II)若在该样本“生根不足量”的植株中随机抽取3株进行进一步检测,求这3株中恰有1株“花卉存活”的概率.
18题参考公式与数据:,
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.(本题满分12分)如图,在几何体ABCDE中,面,,,.
(I)求证:平面平面DAE;
(Ⅱ)AB=1,,,求CE与平面DAE所成角的正弦值.
20.(本题满分12分)已知函数,其中a∈R,设g(x)为f(x)的导函数.
(I)若a=1,求g(x)的最小值:
(II)若时,恒成立,求a的取值范围.
21.(本题满分12分)已知椭圆,过原点作直线与絠圆交于A、B两点,其中位于第一象限,为椭圆上异于A、B的一点.
(I)若AC经过椭圆的右焦点,试求的最大值.
(II)若,记点,试问:B、C、D三点是否共线?请给出判断并说明理由.
(选考题)请在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本题满分10分)在平面直角坐标系xOy中,直线l的参数方程为(为参数),
以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(I)求曲线的直角坐标方程;
(II)若直线与曲线交于M、N两点,求线段MN的长.
23.(本题满分10分)已知函数,.
(I)求函数f(x)的值域;
(Ⅱ)若a>0,b>0,且,不等式恒成立,求实数的取值范围.
成都市名校2022-2023学年高三下学期开学考试
数学试题(文科)参考答案
一、选择题:CBCA CCCDBB CB
二、填空题:13. 14.4 15.5 16.(1) (2)
部分选填题参考解答
10.如图,由题意可知△ODF为等腰三角形,OD=DF,
则,代入渐近线方程,得,又,可得中点,
将其代入双曲线方程,可得,整理可得,∴.
11.联系函数不等式(当且仅当时取等)和(当且仅当时取等),
可得:(1);(2).
从而有.
12.,,,
(1)在,在,在,
则大致图象如图所示,可知方程可能有三个根,故①正确
(2)计算得,则存在,使得,
从而可知在,故②正确
(3)计算得,则,大致图象如图,故③正确
(4)设过原点的直线与相切于点,则有
,,,
消元整理可得,易知此方程无解,故④错误.综上,正确的是①②③.
(说明:由,也可以分析的零点个数)
15.(请同学们结合此题的学习与研究,进一步丰富对抛物线焦点弦的典型性质的认识与积累!)
【解法简介】过作的垂线,交准线于,连接,由,易证平分,则知M即已知中的点P.连接PB,已知PB平分,可推知,则P恰为的中点,故.
【性质积累】(1)可以证明,以焦点弦AB为直径的圆必与准线相切,且切点恰为的中点P;
(2)连接,可以证明恰好与此焦点弦AB相互垂直;
(3)连接,可以证明平分,平分,(图略)
16.(1)由题易知,、均为等边三角形,取它们的中心M、N,过M、N分别作平面、平面的垂线,易知两垂线必交于一点,且点正是三棱锥的外接球球心.(如图所示)
记,则可知二面角的平面角为,在四边形中,可求得,则外接球半径;
(2)当截面面积取最小值时,可知截面,易求得,则截面圆半径,
故其面积.
三、解答题:
17.解:(I)选择①,设等差数列的公差为,则,
由题意可得,即有,解之得,
则.
选择②,设等差数列的公差为,则,
由可,得,解之得,
则.
(II)由(I)可得
所以.
18.解:(I)由题意及数据表可得,
“花卉存活”的有13株,“花卉死亡”的有7株;
“生根足量”的有15株,“生根不足量”的有5株.
①填写列联表:
生根足量 生根不足量 总计
花卉存活 12 1 13
花卉死亡 3 4 7
总计 15 5 20
②应用公式计算得:.
所以不能在犯错误概率不超过1%的前提下,认为“花卉存活”与“生根足量”有关.
(II)样本中“生根不足量”的有5株,其中“花卉死亡”的有4株,记为A,B,C,D;
“花卉存活”的有1株,记为a.设事件A:从5株中随机抽取3株中恰有1株存活,可知其包含的所有情况为:ABC,ABD,ACD,BCD;ABa,ACa,ADa,BCa,BDa,Ca.共10种,其中恰有1株“花卉存活”的情况为ABa,ACa,ADda,BCa,BDa,CDa.共6种.
故所求事件的概率为.
19.解:(I)如图,取的中点M、N,,
连接、、,则知,且,
又,且,
所以,且,
则四边形为平行四边形,所以.
∵,M为的中点,∴,
∵平面,平面,∴.
又,∴平面
从而可得平面,由于平面,
所以平面平面,命题得证.
(II)由(I)知,平面DAE于,则为CE与平面DAE所成角.且在Rt中,,由且,得,
又已知平面,平面,∴,
∵,∴平面ABCD
设,则,那么有,
则,解得,即有.
从而易得,在Rt中,;
又在Rt中,,则知;
∴,即CE与平面DAE所成角的正弦值为.
20.解:(I)时,由,可得,
则,那么有,所以在定义域上单调递增,
注意到,从而可得,,
即知在上单调递减,在上单调递增,
故,即当时,的最小值为0.
(II)由,可得,
由(I),同理可知,在上单调递增,则.讨论如下:
(1)当时,有,则在上单调递增,
从而有,符合题意.
(2)当时,有,由于在上单调递增,
且,所以,使得,
从而可知当时,,则在上单调递减,
此时有,不合题意.
综上,的取值范围为.
21.解:(I)由AC经过椭圆的右焦点,设直线AC的方程为,
联立方程组,消去整理可得,
显然,且有,.
法一:则知,
(说明:此处也可借助椭圆的右焦点半径公式,得到求之)
而原点到直线AC的距离,
由于为线段AB的中点,则到直线AC的距离为2d,
则,其中,
由在上单调递增,故,
当,即时,等号成立,从而可知,的最大值为3.
法二:注意到为线段AB的中点,则,
则有,以下同法一.
(II)B、C、D三点共线,证明如下:
法一:(证明点在直线BC上,即证点的坐标适合直线BC的方程)
一方面,由,两式相减整理可得,
另一方面,,从而可得为定值.
由,得,即有,又,
可得,从而直线BC的方程为,
令,可解得,
即点在直线BC上,故B、C、D三点共线.
法二:(通过坐标运算转化,证明)
由,得,即有,则
同法一,应用“点差法”得到,即有,
又由,,则,
∴,故B、C、D三点共线.
(说明:此问也可通过借助坐标运算证明,得到三点共线,具体方法过程略.)
22.解:(I)由题可得,即有,
结合转换公式,,
代入整理,
经检验,曲线的直角坐标方程为.
(II)由已知易得,直线经过定点,且其倾斜角为,
由此其参数方程也可写为(为参数)(也称之为该直线的标准参数方程),
将其代入,整理可得,显然其,
设M、N两点对应的参数分别为、,则有,,
所以.
(说明:显然,此问也可直接解出参数值求之,或者用直线的普通方程与曲线联立求解之.)
23.解:(I)法一:由题得,
其中,当时,,从而易得函数的值域为.
法二:由绝对值不等式的性质可得,,
所以,当且仅当,即或时取得等号,
故函数的值域为.
(II)法一:由基本不等式,得,
当且仅当时取得等号,故的最小值为2.
法二:由柯西不等式,得,
当且仅当时取得等号,故的最小值为2.
由题得,,即,结合(I)之法一(零点分段,讨论求解)
等价于或或,由此可解得,故原不等式的解集为.
同课章节目录
