5.2运动的合成和分解 同步练习(含答案)
文档属性
| 名称 | 5.2运动的合成和分解 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 206.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-21 00:00:00 | ||
图片预览



文档简介
5.2运动的合成和分解
、单选题
如图所示是港口常用的旋臂式起重机。当起重机旋臂水平向右保持静止时,吊着货物的天车沿旋臂向右以 的速度匀速行驶,同时天车又使货物沿竖直方向先做匀加速运动,后做匀减速运动。那么,当货物沿竖直方向的速度为 时,货物实际的运动速度大小为( )
A.
如图,飞机与货物以4m/s的速度水平匀速飞行,同时以3m/s的速度匀速收拢绳索将货物接到飞机里,绳索始终竖直,该过程中( )
A.绳索的拉力大于货物的重力 B.货物相对地面做曲线运动
C.货物的速度大小为7m/s D.货物的速度大小为5m/s
汽船以额定功率工作,能获得的船速始终保持5m/s(相对于静水),若河水流速是2m/s不变,则汽船的实际船速大小可能是( )
A.2m/s B.5m/s C.8m/s D.10m/s
一江春水向东流,在沿岸平直,宽度为d的江中,水流速度为 ,船在静水中速度为 ,渡江方向可以选择,则该船( )
A.渡江的最短时间为
B.只有当船头垂直江岸时,渡江的时间才和水速无关
C.当 时,渡江的最短路程为d
D.当 时,渡江的最短路程
河宽420m,船在静水中速度为4m/s,水流速度是3m/s,则船过河的最短时间( )
A.140s B.105s C.84s D.60s
如图所示,有两个相互垂直且等高的水平传送带M和N,传送带M、N做匀速直线运动的速度大小分别为0.6m/s、0.8m/s,方向均已在图中标出,一小煤块(视为质点)离开传送带M前已经与传送带M的速度相同,并平稳地传送到传送带N上。小煤块的质量为1kg,与传送带N的动摩擦因数为0.2,取重力加速度大小 ,传送带N的宽度足够大。下列说法正确的是( )
A.小煤块传送到传送带N前的瞬间,相对传送带N的速度大小为1.4m/s
B.小煤块传送到传送带N上后,经1s与传送带N保持相对静止
C.小煤块在传送带N上滑动的划痕是直线,其长度为0.25m
D.小煤块在传送带N上滑动的过程中,因摩擦产生的热量为1J
一船在静水中的速率为,要渡过宽为d,水流的流速为的河流,则渡河的最短时间为( )
A.
甲、乙两船在静水中航行的速度分别为 和 ,两船从同一渡口过河,已知甲船以最短时间过河,乙船以最短航程过河,结果两船抵达对岸的地点恰好相同。则水的流速为( )
A.
某人以不变的速度垂直于对岸游去,游到河中间时,水流速度变大,则此人渡河所用时间比预定时间( )
A.增加 B.减少 C.不变 D.无法确定
小船在静水中的速度是v,现小船要渡一河流,渡河时小船朝对岸垂直划行,若航行至河中时,河水流速增大,则渡河时间将( )
A.增大 B.减小 C.不变 D.不能确定
、多选题
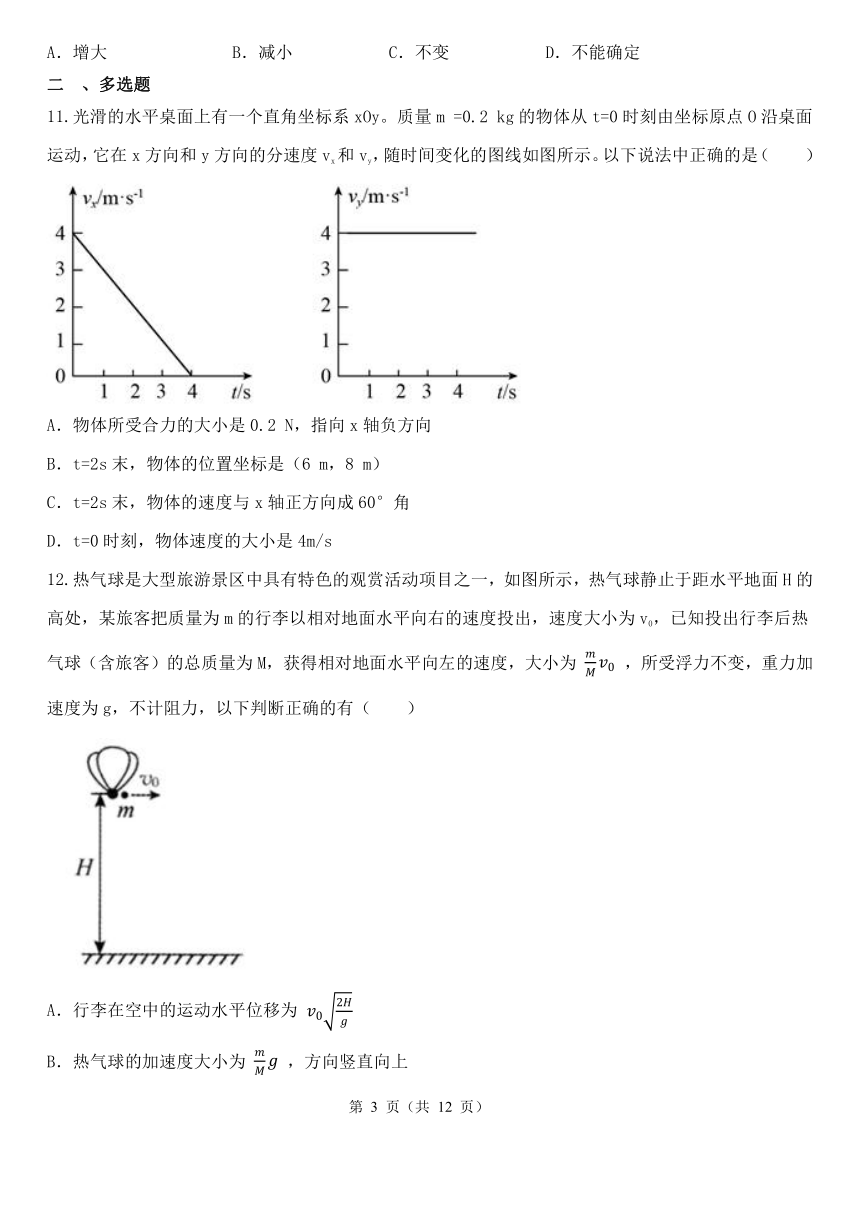
光滑的水平桌面上有一个直角坐标系xOy。质量m =0.2 kg的物体从t=0时刻由坐标原点O沿桌面运动,它在x方向和y方向的分速度vx和vy,随时间变化的图线如图所示。以下说法中正确的是( )
A.物体所受合力的大小是0.2 N,指向x轴负方向
B.t=2s末,物体的位置坐标是(6 m,8 m)
C.t=2s末,物体的速度与x轴正方向成60°角
D.t=0时刻,物体速度的大小是4m/s
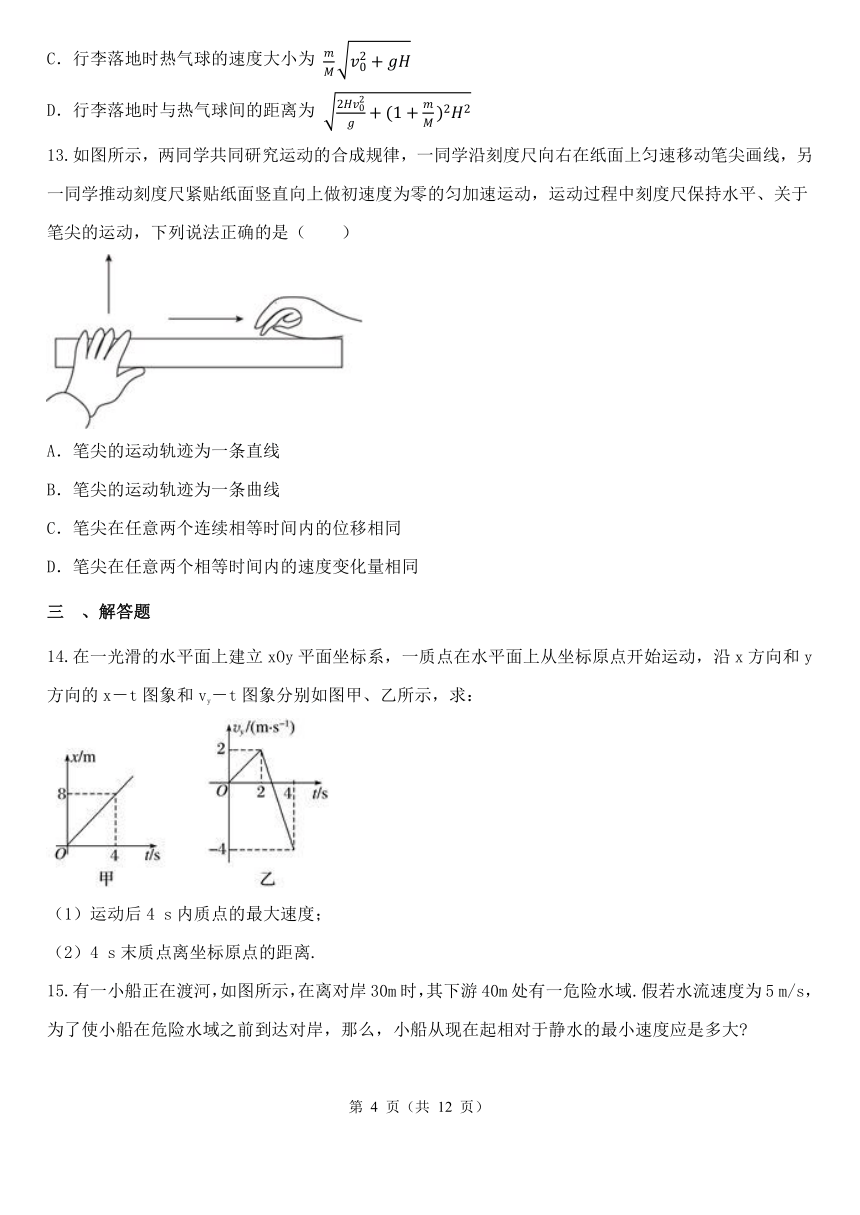
热气球是大型旅游景区中具有特色的观赏活动项目之一,如图所示,热气球静止于距水平地面H的高处,某旅客把质量为m的行李以相对地面水平向右的速度投出,速度大小为v0,已知投出行李后热气球(含旅客)的总质量为M,获得相对地面水平向左的速度,大小为 ,所受浮力不变,重力加速度为g,不计阻力,以下判断正确的有( )
A.行李在空中的运动水平位移为
B.热气球的加速度大小为 ,方向竖直向上
C.行李落地时热气球的速度大小为
D.行李落地时与热气球间的距离为
如图所示,两同学共同研究运动的合成规律,一同学沿刻度尺向右在纸面上匀速移动笔尖画线,另一同学推动刻度尺紧贴纸面竖直向上做初速度为零的匀加速运动,运动过程中刻度尺保持水平、关于笔尖的运动,下列说法正确的是( )
A.笔尖的运动轨迹为一条直线
B.笔尖的运动轨迹为一条曲线
C.笔尖在任意两个连续相等时间内的位移相同
D.笔尖在任意两个相等时间内的速度变化量相同
、解答题
在一光滑的水平面上建立xOy平面坐标系,一质点在水平面上从坐标原点开始运动,沿x方向和y方向的x-t图象和vy-t图象分别如图甲、乙所示,求:
(1)运动后4 s内质点的最大速度;
(2)4 s末质点离坐标原点的距离.
有一小船正在渡河,如图所示,在离对岸30m时,其下游40m处有一危险水域.假若水流速度为5 m/s,为了使小船在危险水域之前到达对岸,那么,小船从现在起相对于静水的最小速度应是多大
5.2运动的合成和分解答案解析
、单选题
【答案】C
【解析】【解答】由题意可知,货物同时参与了水平向右的匀速运动和竖直方向的匀变速运动,设水平向右方向速度为 ,竖直方向速度为 ,当 时,货物实际运动速度的大小为 ,根据速度的合成法则有
解得
故答案为:C。
【分析】结合物体的水平速度和竖直速度,利用勾股定律求解合速度。
【答案】D
【解析】【解答】A.货物在竖直方向上以3m/s的速度匀速向上运动,处于平衡状态,故绳索的拉力等于货物的重力,A不符合题意;
B.货物在水平方向上和竖直方向上均做匀速直线运动,故相对地面的合运动也是匀速直线运动,B不符合题意;
CD.货物对地合运动的速度大小为
C不符合题意,D符合题意。
故答案为:D。
【分析】匀速运动属于平衡状态,二力平衡。各个分运动都是匀速运动,合运动也一定是匀速运动。由勾股定理即可求出合速度大小。
【答案】B
【解析】【解答】船实际的航速是静水速和水流速的合速度,根据平行四边形定则,当船速与水速同向时,实际速度最大为7m/s,当船速与水速反向时,实际速度最小为3m/s,故实际速度的大小范围为。
故答案为:B。
【分析】速度的合成与分解满足平行四边形定则,结合速度的合成与分解进行分析判断汽船的实际船速大小的可能值。
【答案】C
【解析】【解答】A.当船头与河岸垂直时,渡河时间最短,其为
A不符合题意;
B.依据分运动与合运动相互独立性,不论船头如何渡江,渡江的时间都与水速无关,B不符合题意;
CD.当 时,则有合速度与河岸垂直,此时渡河位移最小,因此最短路程为d,D不符合题意,C符合题意。
故答案为:C。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】B
【解析】【解答】船参与了两个分运动,沿船头指向的分运动和沿水流方向的分运动,渡河时间等于沿船头指向分运动的时间,当船头与河岸垂直时,沿船头方向的分运动的位移最小,故渡河时间最短,则
故答案为:B。
【分析】把小车的速度分解到沿绳子的速度和垂直于绳子的速度,其中沿绳子的速度等于拉物体的速度,再利用几何关系分析速度的变化,确定加速度的方向,进而判断拉力和重力的大小关系。
【答案】C
【解析】【解答】A.小煤块传送到传送带N前的瞬间,相对传送带N的速度大小
A不符合题意;
B.小煤块在传送带N上滑动的过程中,其所受滑动摩擦力大小
方向如图所示。
小煤块相对传送带N做匀减速直线运动,其加速度大小
从小煤块滑上传送带N到小煤块与传送带N保持相对静止的时间
B不符合题意;
C.设小煤块在传送带N上滑动的划痕的长度为x,根据匀变速直线运动的规律有
解得
C符合题意:
D.小煤块在传送带N上滑动的过程中,因摩擦产生的热量
D不符合题意。
故答案为:C。
【分析】根据速度的合成得出相对传送带N的速度,根据牛顿第二定律以及匀变速直线运动的规律得出小煤块滑上传送带N到小煤块与传送带N保持相对静止的时间,以及划痕的长度,通过恒力做功的表达式得出摩擦力产生的热量。
【答案】A
【解析】【解答】当船头指向正对岸时,船渡河时间最短,则最短时间为
故答案为:A.
【分析】利用河岸宽度直接除以船在静水中速度可以求出最短过河时间。
【答案】B
【解析】【解答】由题意,甲船以最短时间过河,乙船以最短航程过河,结果两船抵达对岸的地点恰好相同,可知,甲乙实际速度方向一样,如图所示
可得
两式相乘,得
则 ,解得v水=3.75m/s,B符合题意,ACD不符合题意。
故答案为:B。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】C
【解析】【解答】将游泳者的运动分解为沿河岸方向和垂直于河岸方向,因为人以不变的速度向着对岸垂直游去,垂直于河岸方向上的分速度不变,水流速度不影响垂直于河岸方向上的运动,所以渡河时间不变.C符合题意,ABD不符合题意.
故答案为:C.
【分析】利用垂直河岸的宽度除以游泳者的速度可以求出过河时间,与河流速度大小无关。
【答案】C
【解析】【解答】小船的渡河时间取决于小船垂直河岸的分速度大小,与平行河岸的分速度大小无关。水流速度变化,只改变小船平行河岸的分速度大小,不改变小船垂直河岸的分速度大小,所以小船渡河时间不变,C符合题意,ABD不符合题意。
故答案为:C。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
、多选题
【答案】A,B
【解析】【解答】A.在x方向做匀减速运动,在y方向做匀速运动,则合外力方向沿x轴负方向,合外力大小为
A符合题意;
B.t=2s末,物体在x方向的位移为
在y方向的位移为
则位置坐标是(6 m,8 m)B符合题意;
C.t=2s末,物体的速度与x轴正方向成
则速度与x轴正方向成的角不是 60°,C不符合题意;
D.t=0时刻,物体速度的大小是
D不符合题意。
故答案为:AB。
【分析】利用x方向的匀减速直线运动可以求出加速度的大小,结合牛顿第二定律可以求出合力的大小;其y方向做匀速直线运动;利用图像面积可以求出位移的大小,利用速度的大小可以求出速度的方向,利用速度的合成可以求出合速度的大小。
【答案】A,B
【解析】【解答】A.行李在空中做平抛运动,根据 ,
得到水平位移
A符合题意;
B.一开始,热气球静止说明浮力
行李抛出后
得到此时的加速度
B符合题意;
C.行李落地时,热气球竖直方向的速度
合速度
即有
C不符合题意;
D.热气球水平位移
竖直位移
行李与热气球连线始终经过行李抛出点,所以两者距离为
即有
D不符合题意。
故答案为:AB。
【分析】AC.行李做到是平抛运动,利用平抛运动规律及可求出行李的水平位移以及落地速度。
B.热气球抛出行李后,其重力减小,但是其受到的升力大小不变,根据牛顿第二定律就可以列式求解加速度。
D.对两者运动情况进行受力分析,可以利用画草图形式就可以找到两者位置关系。
【答案】B,D
【解析】【解答】AB.向右的匀速运动与向上做初速度为零的匀加速运动的合运动是曲线运动,所以笔尖的运动轨迹为一条曲线。A不符合题意,B符合题意;
C.因为笔尖做匀变速曲线运动,所以笔尖在任意两个连续相等时间内的位移不相同。C不符合题意;
D.因为加速度恒定,所以笔尖在任意两个相等时间内的速度变化量相同。D符合题意。
故答案为:BD。
【分析】这里是两个运动的合成“水平的匀速直线运动和竖直方向的匀加速直线运动”,由此得到和运动的速度变化规律和位移变化规律。
、解答题
【答案】(1)解:由题图可知,质点沿x轴正方向做匀速直线运动,速度大小为vx= =2 m/s,在运动后4 s内,沿y轴方向运动的最大速度为4 m/s,则运动后4 s内质点运动的最大速度有vm= m/s
(2)解:0~2 s内质点沿y轴正方向做匀加速直线运动,2~4 s内先沿y轴正方向做匀减速直线运动,再沿y轴负方向做初速度为零的匀加速直线运动,此时加速度大小为:a= m/s2=3 m/s2
则质点沿y轴正方向做匀减速运动的时间t2= s
则运动后的4 s内沿y轴方向的位移
因此4 s末质点离坐标原点的距离等于沿x轴方向的位移
由题图甲可知,4 s末质点离坐标原点的距离s=x=8 m
【解析】【分析】解决本题的关键要掌握运动的合成和分解,研究质点的运动情况.求位移时要注意的正负,图象在时间轴上方时表示的位移为正,在时间轴下方时表示的位移为负.
【答案】解:设船相对于静水的速度为v1,水速为v2,船的合速度v的方向(过河方向)与水速夹角为α,如图所示
由几何关系知,当v1垂直于v时,v1才最小,此时v1=v2sinα
由题意知sinα最小值为 ,所以v1最小值为vmin=5× m/s=3m/s
故当船在静水中的速度v1与v垂直,且船沿危险临界线航行时,v1最小,此时v1=vmin=3m/s
【解析】【分析】利用速度的合成结合平行四边形定则可以求出最小的速度。
第 1 页(共 1 页)
、单选题
如图所示是港口常用的旋臂式起重机。当起重机旋臂水平向右保持静止时,吊着货物的天车沿旋臂向右以 的速度匀速行驶,同时天车又使货物沿竖直方向先做匀加速运动,后做匀减速运动。那么,当货物沿竖直方向的速度为 时,货物实际的运动速度大小为( )
A.
如图,飞机与货物以4m/s的速度水平匀速飞行,同时以3m/s的速度匀速收拢绳索将货物接到飞机里,绳索始终竖直,该过程中( )
A.绳索的拉力大于货物的重力 B.货物相对地面做曲线运动
C.货物的速度大小为7m/s D.货物的速度大小为5m/s
汽船以额定功率工作,能获得的船速始终保持5m/s(相对于静水),若河水流速是2m/s不变,则汽船的实际船速大小可能是( )
A.2m/s B.5m/s C.8m/s D.10m/s
一江春水向东流,在沿岸平直,宽度为d的江中,水流速度为 ,船在静水中速度为 ,渡江方向可以选择,则该船( )
A.渡江的最短时间为
B.只有当船头垂直江岸时,渡江的时间才和水速无关
C.当 时,渡江的最短路程为d
D.当 时,渡江的最短路程
河宽420m,船在静水中速度为4m/s,水流速度是3m/s,则船过河的最短时间( )
A.140s B.105s C.84s D.60s
如图所示,有两个相互垂直且等高的水平传送带M和N,传送带M、N做匀速直线运动的速度大小分别为0.6m/s、0.8m/s,方向均已在图中标出,一小煤块(视为质点)离开传送带M前已经与传送带M的速度相同,并平稳地传送到传送带N上。小煤块的质量为1kg,与传送带N的动摩擦因数为0.2,取重力加速度大小 ,传送带N的宽度足够大。下列说法正确的是( )
A.小煤块传送到传送带N前的瞬间,相对传送带N的速度大小为1.4m/s
B.小煤块传送到传送带N上后,经1s与传送带N保持相对静止
C.小煤块在传送带N上滑动的划痕是直线,其长度为0.25m
D.小煤块在传送带N上滑动的过程中,因摩擦产生的热量为1J
一船在静水中的速率为,要渡过宽为d,水流的流速为的河流,则渡河的最短时间为( )
A.
甲、乙两船在静水中航行的速度分别为 和 ,两船从同一渡口过河,已知甲船以最短时间过河,乙船以最短航程过河,结果两船抵达对岸的地点恰好相同。则水的流速为( )
A.
某人以不变的速度垂直于对岸游去,游到河中间时,水流速度变大,则此人渡河所用时间比预定时间( )
A.增加 B.减少 C.不变 D.无法确定
小船在静水中的速度是v,现小船要渡一河流,渡河时小船朝对岸垂直划行,若航行至河中时,河水流速增大,则渡河时间将( )
A.增大 B.减小 C.不变 D.不能确定
、多选题
光滑的水平桌面上有一个直角坐标系xOy。质量m =0.2 kg的物体从t=0时刻由坐标原点O沿桌面运动,它在x方向和y方向的分速度vx和vy,随时间变化的图线如图所示。以下说法中正确的是( )
A.物体所受合力的大小是0.2 N,指向x轴负方向
B.t=2s末,物体的位置坐标是(6 m,8 m)
C.t=2s末,物体的速度与x轴正方向成60°角
D.t=0时刻,物体速度的大小是4m/s
热气球是大型旅游景区中具有特色的观赏活动项目之一,如图所示,热气球静止于距水平地面H的高处,某旅客把质量为m的行李以相对地面水平向右的速度投出,速度大小为v0,已知投出行李后热气球(含旅客)的总质量为M,获得相对地面水平向左的速度,大小为 ,所受浮力不变,重力加速度为g,不计阻力,以下判断正确的有( )
A.行李在空中的运动水平位移为
B.热气球的加速度大小为 ,方向竖直向上
C.行李落地时热气球的速度大小为
D.行李落地时与热气球间的距离为
如图所示,两同学共同研究运动的合成规律,一同学沿刻度尺向右在纸面上匀速移动笔尖画线,另一同学推动刻度尺紧贴纸面竖直向上做初速度为零的匀加速运动,运动过程中刻度尺保持水平、关于笔尖的运动,下列说法正确的是( )
A.笔尖的运动轨迹为一条直线
B.笔尖的运动轨迹为一条曲线
C.笔尖在任意两个连续相等时间内的位移相同
D.笔尖在任意两个相等时间内的速度变化量相同
、解答题
在一光滑的水平面上建立xOy平面坐标系,一质点在水平面上从坐标原点开始运动,沿x方向和y方向的x-t图象和vy-t图象分别如图甲、乙所示,求:
(1)运动后4 s内质点的最大速度;
(2)4 s末质点离坐标原点的距离.
有一小船正在渡河,如图所示,在离对岸30m时,其下游40m处有一危险水域.假若水流速度为5 m/s,为了使小船在危险水域之前到达对岸,那么,小船从现在起相对于静水的最小速度应是多大
5.2运动的合成和分解答案解析
、单选题
【答案】C
【解析】【解答】由题意可知,货物同时参与了水平向右的匀速运动和竖直方向的匀变速运动,设水平向右方向速度为 ,竖直方向速度为 ,当 时,货物实际运动速度的大小为 ,根据速度的合成法则有
解得
故答案为:C。
【分析】结合物体的水平速度和竖直速度,利用勾股定律求解合速度。
【答案】D
【解析】【解答】A.货物在竖直方向上以3m/s的速度匀速向上运动,处于平衡状态,故绳索的拉力等于货物的重力,A不符合题意;
B.货物在水平方向上和竖直方向上均做匀速直线运动,故相对地面的合运动也是匀速直线运动,B不符合题意;
CD.货物对地合运动的速度大小为
C不符合题意,D符合题意。
故答案为:D。
【分析】匀速运动属于平衡状态,二力平衡。各个分运动都是匀速运动,合运动也一定是匀速运动。由勾股定理即可求出合速度大小。
【答案】B
【解析】【解答】船实际的航速是静水速和水流速的合速度,根据平行四边形定则,当船速与水速同向时,实际速度最大为7m/s,当船速与水速反向时,实际速度最小为3m/s,故实际速度的大小范围为。
故答案为:B。
【分析】速度的合成与分解满足平行四边形定则,结合速度的合成与分解进行分析判断汽船的实际船速大小的可能值。
【答案】C
【解析】【解答】A.当船头与河岸垂直时,渡河时间最短,其为
A不符合题意;
B.依据分运动与合运动相互独立性,不论船头如何渡江,渡江的时间都与水速无关,B不符合题意;
CD.当 时,则有合速度与河岸垂直,此时渡河位移最小,因此最短路程为d,D不符合题意,C符合题意。
故答案为:C。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】B
【解析】【解答】船参与了两个分运动,沿船头指向的分运动和沿水流方向的分运动,渡河时间等于沿船头指向分运动的时间,当船头与河岸垂直时,沿船头方向的分运动的位移最小,故渡河时间最短,则
故答案为:B。
【分析】把小车的速度分解到沿绳子的速度和垂直于绳子的速度,其中沿绳子的速度等于拉物体的速度,再利用几何关系分析速度的变化,确定加速度的方向,进而判断拉力和重力的大小关系。
【答案】C
【解析】【解答】A.小煤块传送到传送带N前的瞬间,相对传送带N的速度大小
A不符合题意;
B.小煤块在传送带N上滑动的过程中,其所受滑动摩擦力大小
方向如图所示。
小煤块相对传送带N做匀减速直线运动,其加速度大小
从小煤块滑上传送带N到小煤块与传送带N保持相对静止的时间
B不符合题意;
C.设小煤块在传送带N上滑动的划痕的长度为x,根据匀变速直线运动的规律有
解得
C符合题意:
D.小煤块在传送带N上滑动的过程中,因摩擦产生的热量
D不符合题意。
故答案为:C。
【分析】根据速度的合成得出相对传送带N的速度,根据牛顿第二定律以及匀变速直线运动的规律得出小煤块滑上传送带N到小煤块与传送带N保持相对静止的时间,以及划痕的长度,通过恒力做功的表达式得出摩擦力产生的热量。
【答案】A
【解析】【解答】当船头指向正对岸时,船渡河时间最短,则最短时间为
故答案为:A.
【分析】利用河岸宽度直接除以船在静水中速度可以求出最短过河时间。
【答案】B
【解析】【解答】由题意,甲船以最短时间过河,乙船以最短航程过河,结果两船抵达对岸的地点恰好相同,可知,甲乙实际速度方向一样,如图所示
可得
两式相乘,得
则 ,解得v水=3.75m/s,B符合题意,ACD不符合题意。
故答案为:B。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】C
【解析】【解答】将游泳者的运动分解为沿河岸方向和垂直于河岸方向,因为人以不变的速度向着对岸垂直游去,垂直于河岸方向上的分速度不变,水流速度不影响垂直于河岸方向上的运动,所以渡河时间不变.C符合题意,ABD不符合题意.
故答案为:C.
【分析】利用垂直河岸的宽度除以游泳者的速度可以求出过河时间,与河流速度大小无关。
【答案】C
【解析】【解答】小船的渡河时间取决于小船垂直河岸的分速度大小,与平行河岸的分速度大小无关。水流速度变化,只改变小船平行河岸的分速度大小,不改变小船垂直河岸的分速度大小,所以小船渡河时间不变,C符合题意,ABD不符合题意。
故答案为:C。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
、多选题
【答案】A,B
【解析】【解答】A.在x方向做匀减速运动,在y方向做匀速运动,则合外力方向沿x轴负方向,合外力大小为
A符合题意;
B.t=2s末,物体在x方向的位移为
在y方向的位移为
则位置坐标是(6 m,8 m)B符合题意;
C.t=2s末,物体的速度与x轴正方向成
则速度与x轴正方向成的角不是 60°,C不符合题意;
D.t=0时刻,物体速度的大小是
D不符合题意。
故答案为:AB。
【分析】利用x方向的匀减速直线运动可以求出加速度的大小,结合牛顿第二定律可以求出合力的大小;其y方向做匀速直线运动;利用图像面积可以求出位移的大小,利用速度的大小可以求出速度的方向,利用速度的合成可以求出合速度的大小。
【答案】A,B
【解析】【解答】A.行李在空中做平抛运动,根据 ,
得到水平位移
A符合题意;
B.一开始,热气球静止说明浮力
行李抛出后
得到此时的加速度
B符合题意;
C.行李落地时,热气球竖直方向的速度
合速度
即有
C不符合题意;
D.热气球水平位移
竖直位移
行李与热气球连线始终经过行李抛出点,所以两者距离为
即有
D不符合题意。
故答案为:AB。
【分析】AC.行李做到是平抛运动,利用平抛运动规律及可求出行李的水平位移以及落地速度。
B.热气球抛出行李后,其重力减小,但是其受到的升力大小不变,根据牛顿第二定律就可以列式求解加速度。
D.对两者运动情况进行受力分析,可以利用画草图形式就可以找到两者位置关系。
【答案】B,D
【解析】【解答】AB.向右的匀速运动与向上做初速度为零的匀加速运动的合运动是曲线运动,所以笔尖的运动轨迹为一条曲线。A不符合题意,B符合题意;
C.因为笔尖做匀变速曲线运动,所以笔尖在任意两个连续相等时间内的位移不相同。C不符合题意;
D.因为加速度恒定,所以笔尖在任意两个相等时间内的速度变化量相同。D符合题意。
故答案为:BD。
【分析】这里是两个运动的合成“水平的匀速直线运动和竖直方向的匀加速直线运动”,由此得到和运动的速度变化规律和位移变化规律。
、解答题
【答案】(1)解:由题图可知,质点沿x轴正方向做匀速直线运动,速度大小为vx= =2 m/s,在运动后4 s内,沿y轴方向运动的最大速度为4 m/s,则运动后4 s内质点运动的最大速度有vm= m/s
(2)解:0~2 s内质点沿y轴正方向做匀加速直线运动,2~4 s内先沿y轴正方向做匀减速直线运动,再沿y轴负方向做初速度为零的匀加速直线运动,此时加速度大小为:a= m/s2=3 m/s2
则质点沿y轴正方向做匀减速运动的时间t2= s
则运动后的4 s内沿y轴方向的位移
因此4 s末质点离坐标原点的距离等于沿x轴方向的位移
由题图甲可知,4 s末质点离坐标原点的距离s=x=8 m
【解析】【分析】解决本题的关键要掌握运动的合成和分解,研究质点的运动情况.求位移时要注意的正负,图象在时间轴上方时表示的位移为正,在时间轴下方时表示的位移为负.
【答案】解:设船相对于静水的速度为v1,水速为v2,船的合速度v的方向(过河方向)与水速夹角为α,如图所示
由几何关系知,当v1垂直于v时,v1才最小,此时v1=v2sinα
由题意知sinα最小值为 ,所以v1最小值为vmin=5× m/s=3m/s
故当船在静水中的速度v1与v垂直,且船沿危险临界线航行时,v1最小,此时v1=vmin=3m/s
【解析】【分析】利用速度的合成结合平行四边形定则可以求出最小的速度。
第 1 页(共 1 页)
