4.1 天地力的综合:万有引力定律 课件 (共34张PPT) 高一下学期物理鲁科版(2019)必修第二册
文档属性
| 名称 | 4.1 天地力的综合:万有引力定律 课件 (共34张PPT) 高一下学期物理鲁科版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-21 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
第一节 天地力的综合:万有引力定律
鲁科2019
高中物理必修二
第四章 万有引力定律及航天
1、地心说
托勒密
观点: 地球是宇宙的中心,并且静止不动,一切行星围绕地球做圆周运动。
2、日心说
哥白尼
观点:太阳是宇宙的中心,并且静止不动,一切行星都围绕太阳做圆周运动。
VS
“日心说”相对“地心说”能更完美地解释天体的运动,但这两种学说都不完善,因为太阳、地球等天体都是运动的。
日心说的进一步完善
第 谷
被称为:“星学之王” 。第谷进行了长达20多年的观测和研究,积累了大量的关于行星运动的资料,为开普勒的研究提供了重要的数据。
开普勒
被称为“数学天才”。通过对大量数据的分析和计算,认为行星轨道为椭圆。
一、开普勒三大定律
1.开普勒第一定律(轨道定律):所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
F(焦点)
地球
a(半长轴)
F(焦点)
F
F
注意:不同行星绕太阳运行的椭圆轨道不一样,但这些轨道有一个共同的焦点,即太阳所处的位置。
第一定律说明了行星运动轨迹的形状,那不同的行星绕大阳运行时椭圆轨道相同吗
对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
2.开普勒第二定律 (面积定律)
离太阳近时速度快,离太阳远时速度慢。
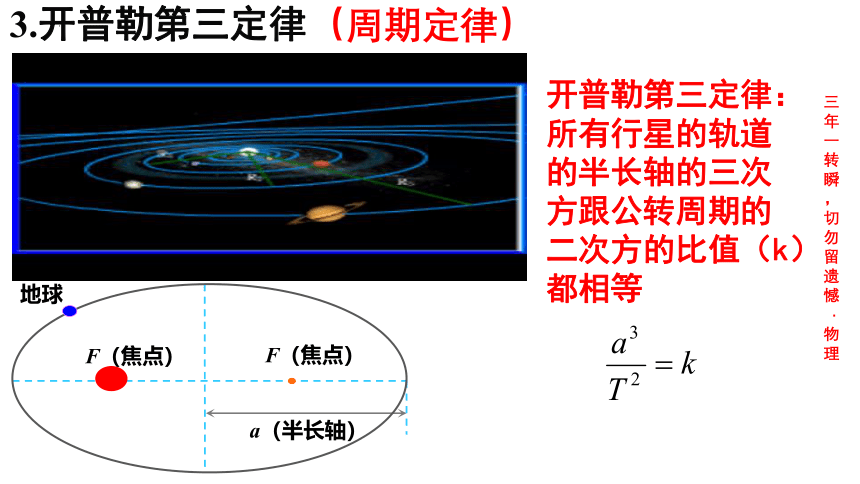
开普勒第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值(k)都相等
3.开普勒第三定律(周期定律)
F(焦点)
地球
a(半长轴)
F(焦点)
思考:比值k取决于什么因素?
行星 半长轴(×106km) 公转周期(天) K值
水星 57.9 87.9 3.36×1018
金星 108.2 224.7 3.36×1018
地球 149.6 365.0 3.37×1018
火星 227.9 693.5
木星 778.0 4307.0
土星 1472.0 10767.5
天王星 2870.0 30660.0
海王星 4496.0 60152.0
同步卫星 0.0424 1.0
月球 0.3844 27.3
3.30×1018
3.40×1018
3.69×1018
3.37×1018
3.36×1018
1.02×1013
1.02×1013
比值k是与行星无关而只与中心天体有关的恒量.
开普勒定律不仅适用于行星绕太阳运动,同时它适用于所有的天体运动。
思考:地球绕太阳运动和月球绕地球运动的两个运动,k值相同吗?
结论: k值与中心天体有关,而与环绕天体无关.
八大行星绕太阳运动的有关数据
a 是年的单位符号。
偏心率 e是椭圆扁平程度的量度,等于椭圆两焦点间的距离与长轴长度的比值。圆是椭圆的特例,偏心率为0。
在中学阶段,我们将椭圆轨道按照圆形轨道处理,则开普勒定律描述为:
1.行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
1.所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
2. 对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
2.对于某一行星来说,它绕太阳做圆周运动的角速度(或线速度)不变,即行星做匀速圆周运动。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等即
例1. 某行星绕太阳运动的轨道如图所示,则以下说法不正确的是( )
A 太阳一定在椭圆的一个焦点上
B.该行星在a点的速度比在b,c两点的速度都大。
C.该行星在c点的速度比在a,b两点的速度都大。
D.行星与太阳的连线在相等的时间内扫过的面积是相等的。
C
太阳
a
b
c
与自转周期无关
a 最大
a 3/ T2 =k
例2. 关于行星的运动,下列说法正确的有是 ( )
A . 行星轨道的半长轴越长,自转的周期就越大
B . 行星轨道的半长轴越长,公转的周期就越大
C . 行星轨道的半长轴越短,公转的周期就越大
D .“冥王星”离太阳最远,绕太阳运动的公转 周期最长
例3. 地球绕太阳运动的轨道是椭圆,因而地球与太阳之间的距离随季节变化,若认为冬至这天地球离太阳最近,夏至最远,则下列关于地球在这两天的太阳公转时速度大小的说法正确的是( )
A. 地球公转速度是不变的
B. 冬至这天地球公转速度大
C. 夏至这天地球公转速度大
D. 无法确定
B
例4.如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时行星的速率为( )
C
例5. 银河系中有两颗行星绕某恒星运行,从天文望远镜中观察到他们的运转周秋之比是8:1,则他们的轨道半径之比为( )
A2:1 B 4:1
C 8:1 D 1:4
B
知识回顾:
1.行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
1.所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
2. 对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
2.对于某一行星来说,它绕太阳做圆周运动的角速度(或线速度)不变,即行星做匀速圆周运动。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等即
消去v
消去T
讨论
F
太阳
M
行星m
r
v
一.太阳与行星间的引力
圆周运动的知识
开普勒运动定律
牛顿第三定律
②
①
天 体的椭 圆运动
任意的两个物体间
同样适用于
发明微积分 进行数学论证
③
牛顿
哈雷
胡克
苹果落地、高处物体落地、月亮绕地旋转……这些现象引起了牛顿的沉思。
万有引力定律的发现
牛顿的思考:
(1)“天上的力”和“人间的力”是同一种力吗?
(2)地球表面的重力是否能延伸到月球轨道?
牛顿的猜想:
苹果与月球受到的引力可能是同一种力!
目的:地面上的重力与地吸引月球是同一性质的力吗?
在地面上质量为 m 的物体所受的地球引力遵守万有引力定律,则有
式中,M为地球质量,R为地球半径。因此,物体在地面处重力加速度的大小
假设将地面上的物体放到月球绕地球旋转的轨道上,由于月球轨道半径R1是地球半径R的60倍,则物体受地球引力作用产生的加速度 就是它在地面时重力加速度的 .
已知月球与地球的距离 r=384400km、月球的公转周期为27.3天。地球对物体的万有引力计算出的处在月球轨道的物体的加速度,与月球绕地球公转的向心加速度恰好相等。
二.牛顿的月-地检验:
2.表达式:
1.内容:自然界中任何两个物体都相互吸引,引力的方向沿着两物体的连线,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的平方成反比。
★关于r的几点说明:
1. 对于两个质量均匀的球体,r指两个球心之间的距离。
2. 对于两个相距很远的质点,r指两个质点之间的距离。
3. r不能为零。(距离很近的情况不能看为质点)
3.引力常量G:在数值上等于两个质量为1Kg的物体相距1m时相互吸引力的大小。取 G = 6.67×10-11 N·m2/kg2
三.万有引力定律
3.理解:
(1).普遍性:万有引力存在于任何两个物体之间;
(2).相互性:作用力和反作用力;
(3).特殊性:两个物体间的万有引力与物体所在空间和其他物体无关;
(4).适用性(适用范围):只适用于两个质点间的引力。
a).两个质点间的相互作用;
b).可以看作质点的两个物体间的相互作用;
c).若是两个均匀的球体,应是两球心间的距离.
m1
m2
r
例4.如图所示,木星是太阳系中最大的行星,与太阳的距离为7.8×108km,木星和太阳的质量分别为1.9×1027kg和2.0×1030kg。试求木星与太阳之间的万有引力大小。
答案:4.2×1023N
例5.关于万有引力定律的适用范围,下列说法中正确的有( )
A.只适用于天体,不适用于地面的物体
B.只适用于球形物体,不适用于其他形状的物体
C .只适用于质点,不适用于实际物体
D.适用于自然界中任何两个物体之间
万有引力存在于一切物体之间
解析:
迁移思考:粗略研究行星的轨道运动时,通常只考虑太阳对行星的万有引力。木星与地球之间的最近距离约为6.3×108km,地球的质量约为6.0×1024kg。请估算木星与地球之间的万有引力大小,并与木星和太阳之间的万有引力大小作比较。
解析:根据公式 ,可以计算出木星和地球之间的万有引力大小为1.9×1018N。可以看出,木星和地球之间的万有引力大小远远小于木星和太阳之间的万有引力大小,所以行星运动状态的变化主要是由太阳对行星的引力引起的。
三、引力常量的测量—卡文迪许扭称实验
亨利·卡文迪许
卡文迪许实验室
最富有的学者,最博学的富豪
卡文迪许也因此被称为“能称出地球质量的人”
卡文迪许扭秤的测量方法
思考:1.两个1千克的物体间的万有引力很小,它是如何测量的?
2.力很小读数如何解决?
引力常量的测量——扭秤实验----放大法
两次放大及等效的思想
1.扭秤装置把微小力通过杠杆旋转明显反映出来(一次放大);
2.扭转角度(微小形变)通过光标的移动来反映(二次放大),从而确定物体间的万有引力。
巧妙之处:
实验数据:
G值为6.67×10-11 N·m2/kg2
实验意义:
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
②开创了微小量测量的先河,使科学放大思想得到推广;
例题6.如图所示,在距一个质量为M,半径为R,密度均匀的球体表面R处,有一个质量为m的质点。此时M对m的万有引力为F1。当从M中挖去如图所示半径为R/2的球体时,剩下部分对m的万有引力为F2,则F1与F2的比为多少?
【答案】9:7
例7.离地面某一高度h处的重力加速度是地球表面重力加速度的二分之一,则高度h是地球半径的多少倍?
答案:
第一节 天地力的综合:万有引力定律
鲁科2019
高中物理必修二
第四章 万有引力定律及航天
1、地心说
托勒密
观点: 地球是宇宙的中心,并且静止不动,一切行星围绕地球做圆周运动。
2、日心说
哥白尼
观点:太阳是宇宙的中心,并且静止不动,一切行星都围绕太阳做圆周运动。
VS
“日心说”相对“地心说”能更完美地解释天体的运动,但这两种学说都不完善,因为太阳、地球等天体都是运动的。
日心说的进一步完善
第 谷
被称为:“星学之王” 。第谷进行了长达20多年的观测和研究,积累了大量的关于行星运动的资料,为开普勒的研究提供了重要的数据。
开普勒
被称为“数学天才”。通过对大量数据的分析和计算,认为行星轨道为椭圆。
一、开普勒三大定律
1.开普勒第一定律(轨道定律):所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
F(焦点)
地球
a(半长轴)
F(焦点)
F
F
注意:不同行星绕太阳运行的椭圆轨道不一样,但这些轨道有一个共同的焦点,即太阳所处的位置。
第一定律说明了行星运动轨迹的形状,那不同的行星绕大阳运行时椭圆轨道相同吗
对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
2.开普勒第二定律 (面积定律)
离太阳近时速度快,离太阳远时速度慢。
开普勒第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值(k)都相等
3.开普勒第三定律(周期定律)
F(焦点)
地球
a(半长轴)
F(焦点)
思考:比值k取决于什么因素?
行星 半长轴(×106km) 公转周期(天) K值
水星 57.9 87.9 3.36×1018
金星 108.2 224.7 3.36×1018
地球 149.6 365.0 3.37×1018
火星 227.9 693.5
木星 778.0 4307.0
土星 1472.0 10767.5
天王星 2870.0 30660.0
海王星 4496.0 60152.0
同步卫星 0.0424 1.0
月球 0.3844 27.3
3.30×1018
3.40×1018
3.69×1018
3.37×1018
3.36×1018
1.02×1013
1.02×1013
比值k是与行星无关而只与中心天体有关的恒量.
开普勒定律不仅适用于行星绕太阳运动,同时它适用于所有的天体运动。
思考:地球绕太阳运动和月球绕地球运动的两个运动,k值相同吗?
结论: k值与中心天体有关,而与环绕天体无关.
八大行星绕太阳运动的有关数据
a 是年的单位符号。
偏心率 e是椭圆扁平程度的量度,等于椭圆两焦点间的距离与长轴长度的比值。圆是椭圆的特例,偏心率为0。
在中学阶段,我们将椭圆轨道按照圆形轨道处理,则开普勒定律描述为:
1.行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
1.所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
2. 对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
2.对于某一行星来说,它绕太阳做圆周运动的角速度(或线速度)不变,即行星做匀速圆周运动。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等即
例1. 某行星绕太阳运动的轨道如图所示,则以下说法不正确的是( )
A 太阳一定在椭圆的一个焦点上
B.该行星在a点的速度比在b,c两点的速度都大。
C.该行星在c点的速度比在a,b两点的速度都大。
D.行星与太阳的连线在相等的时间内扫过的面积是相等的。
C
太阳
a
b
c
与自转周期无关
a 最大
a 3/ T2 =k
例2. 关于行星的运动,下列说法正确的有是 ( )
A . 行星轨道的半长轴越长,自转的周期就越大
B . 行星轨道的半长轴越长,公转的周期就越大
C . 行星轨道的半长轴越短,公转的周期就越大
D .“冥王星”离太阳最远,绕太阳运动的公转 周期最长
例3. 地球绕太阳运动的轨道是椭圆,因而地球与太阳之间的距离随季节变化,若认为冬至这天地球离太阳最近,夏至最远,则下列关于地球在这两天的太阳公转时速度大小的说法正确的是( )
A. 地球公转速度是不变的
B. 冬至这天地球公转速度大
C. 夏至这天地球公转速度大
D. 无法确定
B
例4.如图所示,某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时行星的速率为( )
C
例5. 银河系中有两颗行星绕某恒星运行,从天文望远镜中观察到他们的运转周秋之比是8:1,则他们的轨道半径之比为( )
A2:1 B 4:1
C 8:1 D 1:4
B
知识回顾:
1.行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
1.所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
2. 对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
2.对于某一行星来说,它绕太阳做圆周运动的角速度(或线速度)不变,即行星做匀速圆周运动。
3.所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等即
消去v
消去T
讨论
F
太阳
M
行星m
r
v
一.太阳与行星间的引力
圆周运动的知识
开普勒运动定律
牛顿第三定律
②
①
天 体的椭 圆运动
任意的两个物体间
同样适用于
发明微积分 进行数学论证
③
牛顿
哈雷
胡克
苹果落地、高处物体落地、月亮绕地旋转……这些现象引起了牛顿的沉思。
万有引力定律的发现
牛顿的思考:
(1)“天上的力”和“人间的力”是同一种力吗?
(2)地球表面的重力是否能延伸到月球轨道?
牛顿的猜想:
苹果与月球受到的引力可能是同一种力!
目的:地面上的重力与地吸引月球是同一性质的力吗?
在地面上质量为 m 的物体所受的地球引力遵守万有引力定律,则有
式中,M为地球质量,R为地球半径。因此,物体在地面处重力加速度的大小
假设将地面上的物体放到月球绕地球旋转的轨道上,由于月球轨道半径R1是地球半径R的60倍,则物体受地球引力作用产生的加速度 就是它在地面时重力加速度的 .
已知月球与地球的距离 r=384400km、月球的公转周期为27.3天。地球对物体的万有引力计算出的处在月球轨道的物体的加速度,与月球绕地球公转的向心加速度恰好相等。
二.牛顿的月-地检验:
2.表达式:
1.内容:自然界中任何两个物体都相互吸引,引力的方向沿着两物体的连线,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的平方成反比。
★关于r的几点说明:
1. 对于两个质量均匀的球体,r指两个球心之间的距离。
2. 对于两个相距很远的质点,r指两个质点之间的距离。
3. r不能为零。(距离很近的情况不能看为质点)
3.引力常量G:在数值上等于两个质量为1Kg的物体相距1m时相互吸引力的大小。取 G = 6.67×10-11 N·m2/kg2
三.万有引力定律
3.理解:
(1).普遍性:万有引力存在于任何两个物体之间;
(2).相互性:作用力和反作用力;
(3).特殊性:两个物体间的万有引力与物体所在空间和其他物体无关;
(4).适用性(适用范围):只适用于两个质点间的引力。
a).两个质点间的相互作用;
b).可以看作质点的两个物体间的相互作用;
c).若是两个均匀的球体,应是两球心间的距离.
m1
m2
r
例4.如图所示,木星是太阳系中最大的行星,与太阳的距离为7.8×108km,木星和太阳的质量分别为1.9×1027kg和2.0×1030kg。试求木星与太阳之间的万有引力大小。
答案:4.2×1023N
例5.关于万有引力定律的适用范围,下列说法中正确的有( )
A.只适用于天体,不适用于地面的物体
B.只适用于球形物体,不适用于其他形状的物体
C .只适用于质点,不适用于实际物体
D.适用于自然界中任何两个物体之间
万有引力存在于一切物体之间
解析:
迁移思考:粗略研究行星的轨道运动时,通常只考虑太阳对行星的万有引力。木星与地球之间的最近距离约为6.3×108km,地球的质量约为6.0×1024kg。请估算木星与地球之间的万有引力大小,并与木星和太阳之间的万有引力大小作比较。
解析:根据公式 ,可以计算出木星和地球之间的万有引力大小为1.9×1018N。可以看出,木星和地球之间的万有引力大小远远小于木星和太阳之间的万有引力大小,所以行星运动状态的变化主要是由太阳对行星的引力引起的。
三、引力常量的测量—卡文迪许扭称实验
亨利·卡文迪许
卡文迪许实验室
最富有的学者,最博学的富豪
卡文迪许也因此被称为“能称出地球质量的人”
卡文迪许扭秤的测量方法
思考:1.两个1千克的物体间的万有引力很小,它是如何测量的?
2.力很小读数如何解决?
引力常量的测量——扭秤实验----放大法
两次放大及等效的思想
1.扭秤装置把微小力通过杠杆旋转明显反映出来(一次放大);
2.扭转角度(微小形变)通过光标的移动来反映(二次放大),从而确定物体间的万有引力。
巧妙之处:
实验数据:
G值为6.67×10-11 N·m2/kg2
实验意义:
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
②开创了微小量测量的先河,使科学放大思想得到推广;
例题6.如图所示,在距一个质量为M,半径为R,密度均匀的球体表面R处,有一个质量为m的质点。此时M对m的万有引力为F1。当从M中挖去如图所示半径为R/2的球体时,剩下部分对m的万有引力为F2,则F1与F2的比为多少?
【答案】9:7
例7.离地面某一高度h处的重力加速度是地球表面重力加速度的二分之一,则高度h是地球半径的多少倍?
答案:
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
