17.3.3一次函数的性质 课件(共24张PPT)
文档属性
| 名称 | 17.3.3一次函数的性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-21 08:31:41 | ||
图片预览





文档简介
(共24张PPT)
17.3.3一次函数的性质
华师大版 八年级 下册
教学目标
教学目标:1.会画一次函数的图象,能根据一次函数的图象归纳总结出
图象经过象限的规律并理解一次函数的增减性.
2.能灵活运用一次函数的图象与性质解答有关问题.
教学重点:掌握一次函数图象的性质.
教学难点:掌握一次函数图象的性质.
新知导入
情境引入
1、一次函数的一般形式是什么?
y=kx+b(k,b为常数,k≠0).
2、一次函数的图象是什么?
一条直线.
3、直线 y=kx+b与x轴的交点坐标是 ,与y轴的交点坐标是 .
(0,b)
b决定了图象与y轴的交点位置:
b>0时,图象与y轴的交点在x轴的上方;
b<0时,图象与y轴的交点在x轴的下方;
b=0时,图象与y轴的交点就是原点.
( ,0)
新知讲解
合作学习
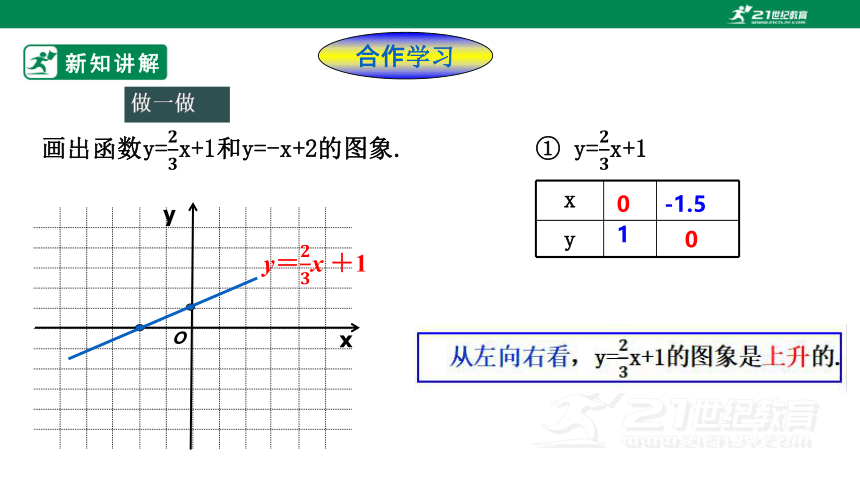
画出函数y=x+1和y=-x+2的图象.
① y=x+1
x
y
0
-1.5
1
0
x
y
y=x +1
做一做
O
x
y
–1
–1
y = x + 1
2
3
函数值 y 随自变量 x 的增大而______.
增大
–1
O
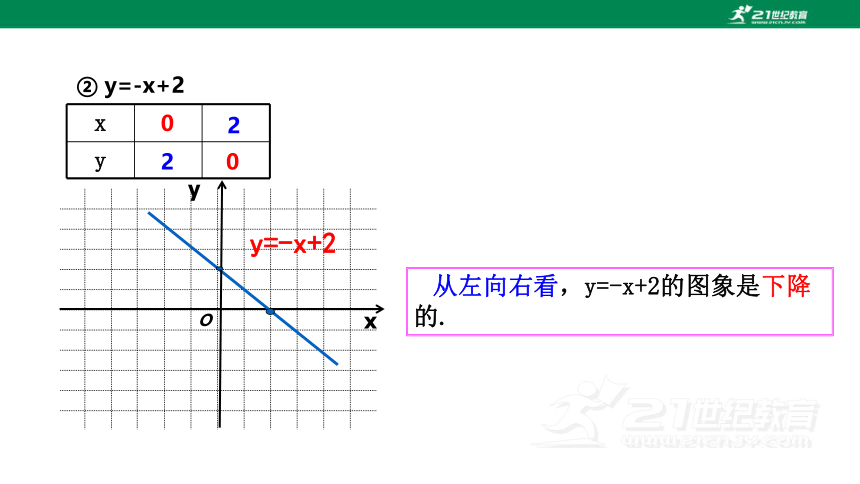
② y=-x+2
x
y
x
y
0
2
2
0
y=-x+2
从左向右看,y=-x+2的图象是下降的.
O
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=-x+2
y=- x-1
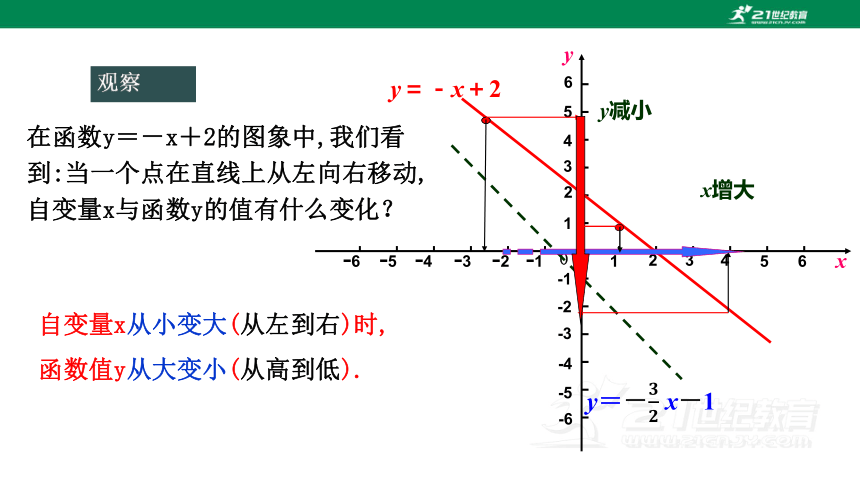
x增大
y减小
在函数y=-x+2的图象中,我们看到:当一个点在直线上从左向右移动,自变量x与函数y的值有什么变化?
自变量x从小变大(从左到右)时, 函数值y从大变小(从高到低).
观察
思考
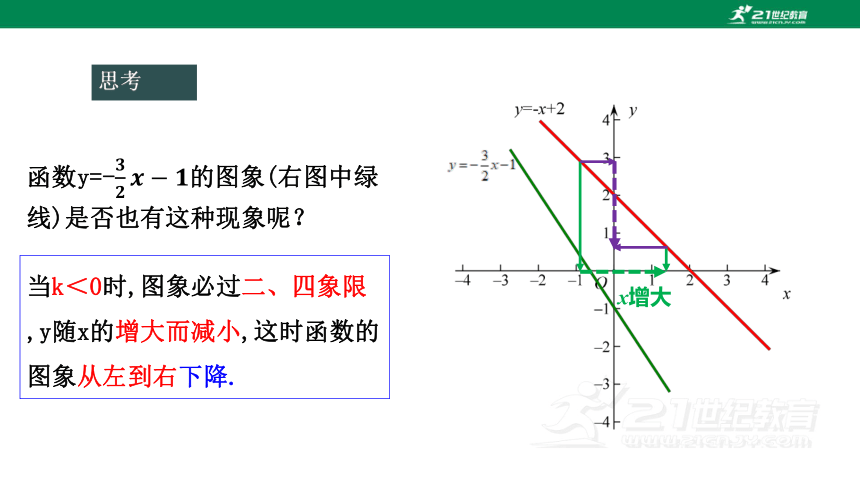
x增大
当k<0时,图象必过二、四象限,y随x的增大而减小,这时函数的图象从左到右下降.
函数y=-的图象(右图中绿线)是否也有这种现象呢?
两条直线都经过二、四象限,且当b>0时,直线与x轴的交点在y轴的正半轴,或在x轴的上方;当b<0时,直线与x轴的交点在y轴的负半轴,或在x轴的下方.所以当k<0,b≠0时,直线经过二、四、一象限或经过二、四、三象限.
提炼概念
一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
(2)当k<0时,y随x的增大而减小,这时函数的图象从左到右下降.
特别地,当b=0时,正比例函数也有上述性质.
当b>0,直线与y轴交于正半轴;
当b<0时,直线与y轴交于负半轴.
y=kx+b 图 象 性 质 直线经过的象限 增减性
k>0 b>0
b=0
b<0
第一、三象限
y随x增大
而增大
第一、二、三象限
y随x增大
而增大
第一、三、四象限
y随x增大
而增大
(0,b)
(0, b)
y=kx+b 图 象 性 质 直线经过的象限 增减性
k<0 b>0
b=0
b<0
第二、四象限
y随x增大
而减小
第一、二、四象限
y随x增大
而减小
第一、三、四象限
y随x增大
而增大
(0,b)
(0, b)
典例精讲
例 画出函数y=-2x+2的图象,结合图象回答下列问题:
(1)这个函数中,随着x的增大,y将增大还是减小 它的图象从左到右怎样变化
(2)当x取何值时,y=0
(3)当x取何值时,y>0
解:(1)这个函数中, y随x的增大而减小,这时函数的图象从左到右是下降的;(2)当x=1时, y=0;(3)当x<1,y>0.
归纳概念
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
课堂练习
1. 一次函数y=x-2的大致图象为( )
C
A B C D
x
O
D
x
O
C
y
x
O
B
2.已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
B
y
y
y
x
O
A
分析:由函数 y = kx的图象在二、四象限,可知k<0,所以-k>0,所以数y = kx-k的图象经过第一、二、四象限,故选B.
3. P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 B. y1<y2 C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
D
4.已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是﹣2≤y≤4,则kb的值为 .
﹣6或﹣12
5.已知点(2,m) 、(-3,n)都在直线 上,试比较 m和n的大小.你能想出几种判断的方法
解:方法一:把两点的坐标代入函数关系式.
当x=2 时,m= ,当x= -3 时,n= ,
所以m>n.
方法二:因为 K= >0, 所以函数y随x增大而增大.
从而直接得到m>n.
6. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限.
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
课堂总结
一次函数的性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.3.3一次函数的性质
华师大版 八年级 下册
教学目标
教学目标:1.会画一次函数的图象,能根据一次函数的图象归纳总结出
图象经过象限的规律并理解一次函数的增减性.
2.能灵活运用一次函数的图象与性质解答有关问题.
教学重点:掌握一次函数图象的性质.
教学难点:掌握一次函数图象的性质.
新知导入
情境引入
1、一次函数的一般形式是什么?
y=kx+b(k,b为常数,k≠0).
2、一次函数的图象是什么?
一条直线.
3、直线 y=kx+b与x轴的交点坐标是 ,与y轴的交点坐标是 .
(0,b)
b决定了图象与y轴的交点位置:
b>0时,图象与y轴的交点在x轴的上方;
b<0时,图象与y轴的交点在x轴的下方;
b=0时,图象与y轴的交点就是原点.
( ,0)
新知讲解
合作学习
画出函数y=x+1和y=-x+2的图象.
① y=x+1
x
y
0
-1.5
1
0
x
y
y=x +1
做一做
O
x
y
–1
–1
y = x + 1
2
3
函数值 y 随自变量 x 的增大而______.
增大
–1
O
② y=-x+2
x
y
x
y
0
2
2
0
y=-x+2
从左向右看,y=-x+2的图象是下降的.
O
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=-x+2
y=- x-1
x增大
y减小
在函数y=-x+2的图象中,我们看到:当一个点在直线上从左向右移动,自变量x与函数y的值有什么变化?
自变量x从小变大(从左到右)时, 函数值y从大变小(从高到低).
观察
思考
x增大
当k<0时,图象必过二、四象限,y随x的增大而减小,这时函数的图象从左到右下降.
函数y=-的图象(右图中绿线)是否也有这种现象呢?
两条直线都经过二、四象限,且当b>0时,直线与x轴的交点在y轴的正半轴,或在x轴的上方;当b<0时,直线与x轴的交点在y轴的负半轴,或在x轴的下方.所以当k<0,b≠0时,直线经过二、四、一象限或经过二、四、三象限.
提炼概念
一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
(2)当k<0时,y随x的增大而减小,这时函数的图象从左到右下降.
特别地,当b=0时,正比例函数也有上述性质.
当b>0,直线与y轴交于正半轴;
当b<0时,直线与y轴交于负半轴.
y=kx+b 图 象 性 质 直线经过的象限 增减性
k>0 b>0
b=0
b<0
第一、三象限
y随x增大
而增大
第一、二、三象限
y随x增大
而增大
第一、三、四象限
y随x增大
而增大
(0,b)
(0, b)
y=kx+b 图 象 性 质 直线经过的象限 增减性
k<0 b>0
b=0
b<0
第二、四象限
y随x增大
而减小
第一、二、四象限
y随x增大
而减小
第一、三、四象限
y随x增大
而增大
(0,b)
(0, b)
典例精讲
例 画出函数y=-2x+2的图象,结合图象回答下列问题:
(1)这个函数中,随着x的增大,y将增大还是减小 它的图象从左到右怎样变化
(2)当x取何值时,y=0
(3)当x取何值时,y>0
解:(1)这个函数中, y随x的增大而减小,这时函数的图象从左到右是下降的;(2)当x=1时, y=0;(3)当x<1,y>0.
归纳概念
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
课堂练习
1. 一次函数y=x-2的大致图象为( )
C
A B C D
x
O
D
x
O
C
y
x
O
B
2.已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
B
y
y
y
x
O
A
分析:由函数 y = kx的图象在二、四象限,可知k<0,所以-k>0,所以数y = kx-k的图象经过第一、二、四象限,故选B.
3. P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 B. y1<y2 C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
D
4.已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是﹣2≤y≤4,则kb的值为 .
﹣6或﹣12
5.已知点(2,m) 、(-3,n)都在直线 上,试比较 m和n的大小.你能想出几种判断的方法
解:方法一:把两点的坐标代入函数关系式.
当x=2 时,m= ,当x= -3 时,n= ,
所以m>n.
方法二:因为 K= >0, 所以函数y随x增大而增大.
从而直接得到m>n.
6. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限.
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
课堂总结
一次函数的性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
