(人教B版)高中数学必修5-3-5-2课后强化作业(含答案)
文档属性
| 名称 | (人教B版)高中数学必修5-3-5-2课后强化作业(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 314.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-28 17:08:38 | ||
图片预览

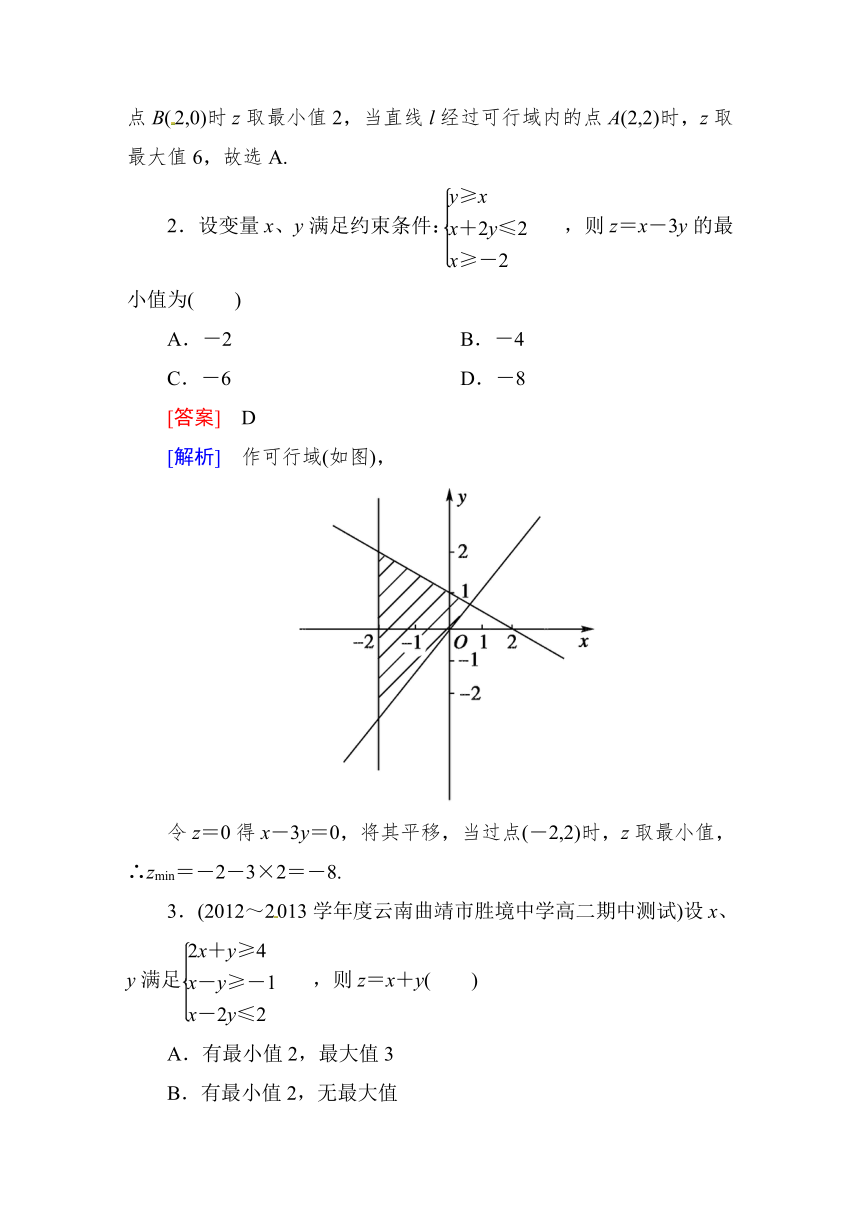


文档简介
基 础 巩 固
一、选择题
1.若x、y满足约束条件,则目标函数z=x+2y的取值范围是( )
A.[2,6] B.[2,5]
C.[3,6] D.[3,5]
[答案] A
[解析] 画出不等式组表示的可行域为如图所示的△ABC.
作直线l:x+2y=0,平行移动直线l,当直线l经过可行域内的点B(2,0)时z取最小值2,当直线l经过可行域内的点A(2,2)时,z取最大值6,故选A.
2.设变量x、y满足约束条件:,则z=x-3y的最小值为( )
A.-2 B.-4
C.-6 D.-8
[答案] D
[解析] 作可行域(如图),
令z=0得x-3y=0,将其平移,当过点(-2,2)时,z取最小值,∴zmin=-2-3×2=-8.
3.(2012~2013学年度云南曲靖市胜境中学高二期中测试)设x、y满足,则z=x+y( )
A.有最小值2,最大值3
B.有最小值2,无最大值
C.有最大值3,无最小值
D.既无最小值,也无最大值
[答案] B[来源:www.]
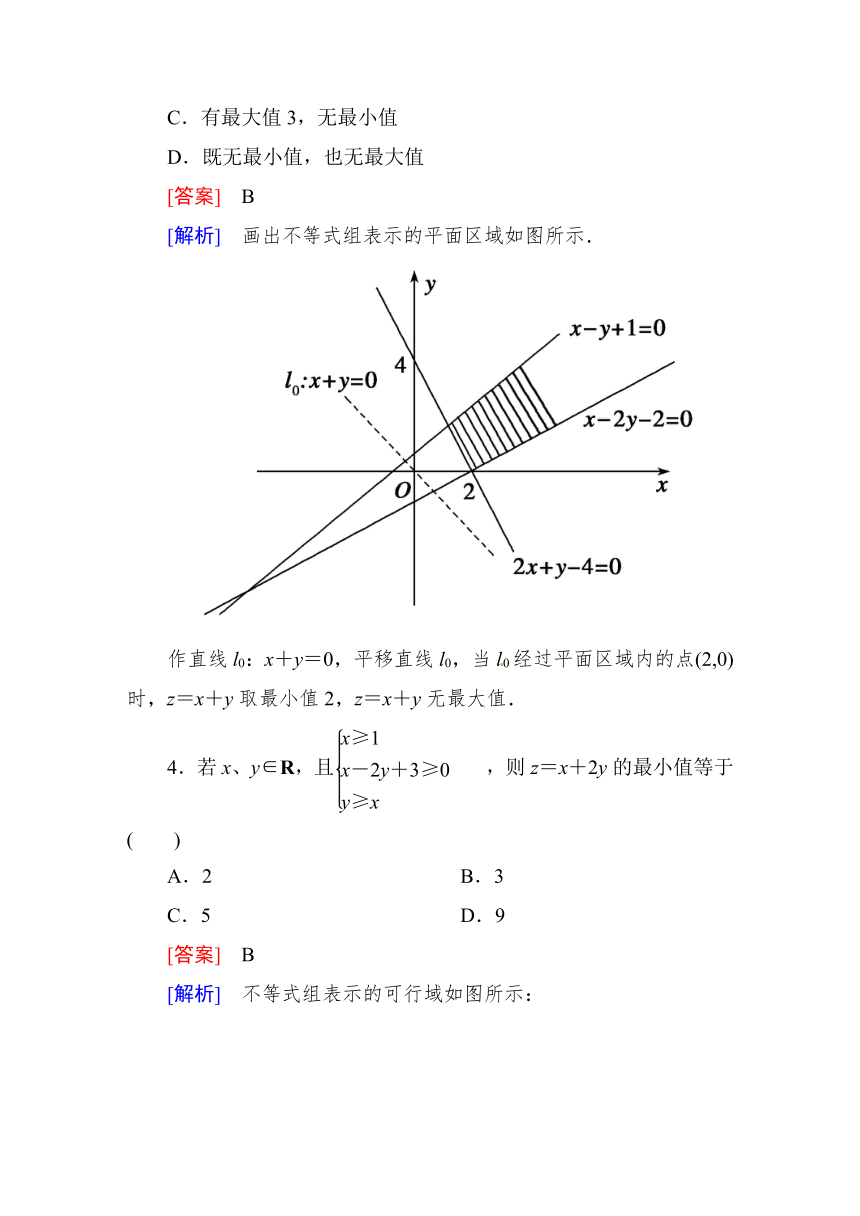
[解析] 画出不等式组表示的平面区域如图所示.
作直线l0:x+y=0,平移直线l0,当l0经过平面区域内的点(2,0)时,z=x+y取最小值2,z=x+y无最大值.
4.若x、y∈R,且,则z=x+2y的最小值等于( )
A.2 B.3
C.5 D.9
[答案] B
[解析] 不等式组表示的可行域如图所示:[来源:www.]
画出l0:x+2y=0;平行移动l0到l的位置,
当l通过M时,z能取到最小值.
此时M(1,1),即zmin=3.
5.(2013·四川文,8)若变量x、y满足约束条件,且z=5y-x的最大值为a,最小值为b,则a-b的值是( )[来源:www.]
A.48 B.30
C.24 D.16
[答案] C
[解析] 本题考查了线性规划中最优解问题.z=5y-x,可得y=x+z.表示直线在y轴上的截距.截距越大z越大,截距载小,z越小,如图所示.
平移直线l0:y=x.
当l0过A点(4,4)时可得zmax=a=16.
当l0过B点(8,0)时可得zmin=b=-8.
故a-b=16-(-8)=24.
6.已知点P(x,y)的坐标满足条件,那么x2+y2的取值范围是( )
A.[1,4] B.[1,5]
C.[,4] D.[,5]
[答案] D
[解析] 不等式组所表示的平面区域,如图中的阴影部分,显然,原点O到直线2x+y-2=0的距离最小,为=,此时可得(x2+y2)min=;点(1,2)到原点O的距离最大,为=,此时可得(x2+y2)max=5.故选D.
二、填空题
7.(2013·安徽文,12)若非负变量x、y满足约束条件,则x+y的最大值为________.
[答案] 4
[解析] 本题考查线性规化的最优解问题.
x、y满足的条件.
画出可行域如图所示.
设x+y=t y=-x+t,t表示直线在y轴截距,截距越大,t越大.
作直线l0:x+y=0,平移直线l0,当l0经过点A(4,0)时, t取最大值4.
8.(2013·山东文,14)在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则|OM|的最小值是________.
[答案]
[解析] 本题考查不等式组表示平面区域及点到直线距离问题.
不等式组所表示平面区域如图,|OM|最小即O到直线x+y-2=0的距离.
故|OM|的最小值为=.
三、解答题
9.在平面直角坐标系中,不等式组(a为正常数)表示的平面区域的面积是4,求2x+y的最大值.
[解析] 由题意得:
S=×2a×a=4,∴a=2.
设z=2x+y,∴y=-2x+z,
由,得(2,2),即z在(2,2)处取得最大值6.[来源:www.www.]
能 力 提 升
一、选择题
1.设变量x、y满足约束条件,则目标函数z=2x+3y+1的最大值为( )
A.11 B.10
C.9 D.8.5
[答案] B
[解析] 作出不等式组表示的可行域,如下图的阴影部分所示.
又z=2x+3y+1可化为y=-x+-,
结合图形可知z=2x+3y+1在点A处取得最大值.
由,得.故A点坐标为(3,1).
此时z=2×3+3×1+1=10.
2.(2012·广东文,5)已知变量x、y满足约束条件,则z=x+2y的最小值为( )
A.3 B.1
C.-5 D.-6
[答案] C
[解析] 本题考查二元一次不等式组表示的平面区域,线性目标函数最值.
由画出可行域如图.
令z=0画出l0:x+2y=0,平移l0至其过A点时z最小,由,得A(-1,-2),
∴zmin=-1+2×(-2)=-5.
二、填空题
3.在△ABC中,三个顶点分别为A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC的内部及其边界上运动,则y-x的取值范围为________.
[答案] [-1,3]
[解析] 画出三角形区域如图,易知kAB=<1,
令z=y-x,则y=x+z,作出直线l0:y=x,平移直线l0,当经过点C时,zmin=-1,当经过点B时,zmax=3,
∴-1≤z≤3.
4.已知点M、N是所围成的平面区域内的两点,则|MN|的最大值是________.
[答案]
[解析] 不等式组表示的平面区域如图中的阴影部分所示,
∵直线x-y+1=0与直线x+y=6垂直,
直线x=1与y=1垂直,
∴|MN|的最大值是|AB|==.
三、解答题
5.已知,求x2+y2的最小值.
[解析] 画出可行域如下图所示,
可见可行域中的点A(1,2)到原点距离最小为d=,∴x2+y2≥5.即x2+y2的最小值为5.[来源:www.]
6.若x、y满足约束条件,目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.
[解析] 画出可行域如图,目标函数z=ax+2y在点(1,0)处取最小值为直线ax+2y-z=0过点(1,0)时在y轴上的截距最小,斜率应满足-1<-<2.
∴a的取值范围是(-4,2).
一、选择题
1.若x、y满足约束条件,则目标函数z=x+2y的取值范围是( )
A.[2,6] B.[2,5]
C.[3,6] D.[3,5]
[答案] A
[解析] 画出不等式组表示的可行域为如图所示的△ABC.
作直线l:x+2y=0,平行移动直线l,当直线l经过可行域内的点B(2,0)时z取最小值2,当直线l经过可行域内的点A(2,2)时,z取最大值6,故选A.
2.设变量x、y满足约束条件:,则z=x-3y的最小值为( )
A.-2 B.-4
C.-6 D.-8
[答案] D
[解析] 作可行域(如图),
令z=0得x-3y=0,将其平移,当过点(-2,2)时,z取最小值,∴zmin=-2-3×2=-8.
3.(2012~2013学年度云南曲靖市胜境中学高二期中测试)设x、y满足,则z=x+y( )
A.有最小值2,最大值3
B.有最小值2,无最大值
C.有最大值3,无最小值
D.既无最小值,也无最大值
[答案] B[来源:www.]
[解析] 画出不等式组表示的平面区域如图所示.
作直线l0:x+y=0,平移直线l0,当l0经过平面区域内的点(2,0)时,z=x+y取最小值2,z=x+y无最大值.
4.若x、y∈R,且,则z=x+2y的最小值等于( )
A.2 B.3
C.5 D.9
[答案] B
[解析] 不等式组表示的可行域如图所示:[来源:www.]
画出l0:x+2y=0;平行移动l0到l的位置,
当l通过M时,z能取到最小值.
此时M(1,1),即zmin=3.
5.(2013·四川文,8)若变量x、y满足约束条件,且z=5y-x的最大值为a,最小值为b,则a-b的值是( )[来源:www.]
A.48 B.30
C.24 D.16
[答案] C
[解析] 本题考查了线性规划中最优解问题.z=5y-x,可得y=x+z.表示直线在y轴上的截距.截距越大z越大,截距载小,z越小,如图所示.
平移直线l0:y=x.
当l0过A点(4,4)时可得zmax=a=16.
当l0过B点(8,0)时可得zmin=b=-8.
故a-b=16-(-8)=24.
6.已知点P(x,y)的坐标满足条件,那么x2+y2的取值范围是( )
A.[1,4] B.[1,5]
C.[,4] D.[,5]
[答案] D
[解析] 不等式组所表示的平面区域,如图中的阴影部分,显然,原点O到直线2x+y-2=0的距离最小,为=,此时可得(x2+y2)min=;点(1,2)到原点O的距离最大,为=,此时可得(x2+y2)max=5.故选D.
二、填空题
7.(2013·安徽文,12)若非负变量x、y满足约束条件,则x+y的最大值为________.
[答案] 4
[解析] 本题考查线性规化的最优解问题.
x、y满足的条件.
画出可行域如图所示.
设x+y=t y=-x+t,t表示直线在y轴截距,截距越大,t越大.
作直线l0:x+y=0,平移直线l0,当l0经过点A(4,0)时, t取最大值4.
8.(2013·山东文,14)在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则|OM|的最小值是________.
[答案]
[解析] 本题考查不等式组表示平面区域及点到直线距离问题.
不等式组所表示平面区域如图,|OM|最小即O到直线x+y-2=0的距离.
故|OM|的最小值为=.
三、解答题
9.在平面直角坐标系中,不等式组(a为正常数)表示的平面区域的面积是4,求2x+y的最大值.
[解析] 由题意得:
S=×2a×a=4,∴a=2.
设z=2x+y,∴y=-2x+z,
由,得(2,2),即z在(2,2)处取得最大值6.[来源:www.www.]
能 力 提 升
一、选择题
1.设变量x、y满足约束条件,则目标函数z=2x+3y+1的最大值为( )
A.11 B.10
C.9 D.8.5
[答案] B
[解析] 作出不等式组表示的可行域,如下图的阴影部分所示.
又z=2x+3y+1可化为y=-x+-,
结合图形可知z=2x+3y+1在点A处取得最大值.
由,得.故A点坐标为(3,1).
此时z=2×3+3×1+1=10.
2.(2012·广东文,5)已知变量x、y满足约束条件,则z=x+2y的最小值为( )
A.3 B.1
C.-5 D.-6
[答案] C
[解析] 本题考查二元一次不等式组表示的平面区域,线性目标函数最值.
由画出可行域如图.
令z=0画出l0:x+2y=0,平移l0至其过A点时z最小,由,得A(-1,-2),
∴zmin=-1+2×(-2)=-5.
二、填空题
3.在△ABC中,三个顶点分别为A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC的内部及其边界上运动,则y-x的取值范围为________.
[答案] [-1,3]
[解析] 画出三角形区域如图,易知kAB=<1,
令z=y-x,则y=x+z,作出直线l0:y=x,平移直线l0,当经过点C时,zmin=-1,当经过点B时,zmax=3,
∴-1≤z≤3.
4.已知点M、N是所围成的平面区域内的两点,则|MN|的最大值是________.
[答案]
[解析] 不等式组表示的平面区域如图中的阴影部分所示,
∵直线x-y+1=0与直线x+y=6垂直,
直线x=1与y=1垂直,
∴|MN|的最大值是|AB|==.
三、解答题
5.已知,求x2+y2的最小值.
[解析] 画出可行域如下图所示,
可见可行域中的点A(1,2)到原点距离最小为d=,∴x2+y2≥5.即x2+y2的最小值为5.[来源:www.]
6.若x、y满足约束条件,目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.
[解析] 画出可行域如图,目标函数z=ax+2y在点(1,0)处取最小值为直线ax+2y-z=0过点(1,0)时在y轴上的截距最小,斜率应满足-1<-<2.
∴a的取值范围是(-4,2).
