2021-2022学年新教材人教A版选择性必修第一册 1.3.1空间直角坐标系 教案
文档属性
| 名称 | 2021-2022学年新教材人教A版选择性必修第一册 1.3.1空间直角坐标系 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 565.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 13:19:16 | ||
图片预览

文档简介
第一章 空间向量与立体几何
1.3 空间向量及其运算的坐标表示
1.3.1 空间直角坐标系
教学设计
一、教学目标
1. 了解空间直角坐标系,会用空间直角坐标系刻画点的位置;
2. 掌握利用坐标表示空间直角坐标系中点的方法.
二、教学重难点
1. 教学重点
空间直角坐标系的建立,空间直角坐标系中点的坐标表示.
2. 教学难点
在空间直角坐标系中画出给定坐标的点的位置.
三、教学过程
(一)新课导入
平面直角坐标系由平面内两条互相垂直、原点重合的数轴组成.如图,在平面内选定一点O和一个单位正交基底{i,j},以O为原点,分别以i,j的方向为正方向、以它们的长为单位长度建立两条数轴:x轴、y轴,那么就建立了一个平面直角坐标系.
类比平面直角坐标系,探究空间直角坐标系.
(二)探索新知
在空间选定一点O和一个单位正交基底{i,j,k}(如图).以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.
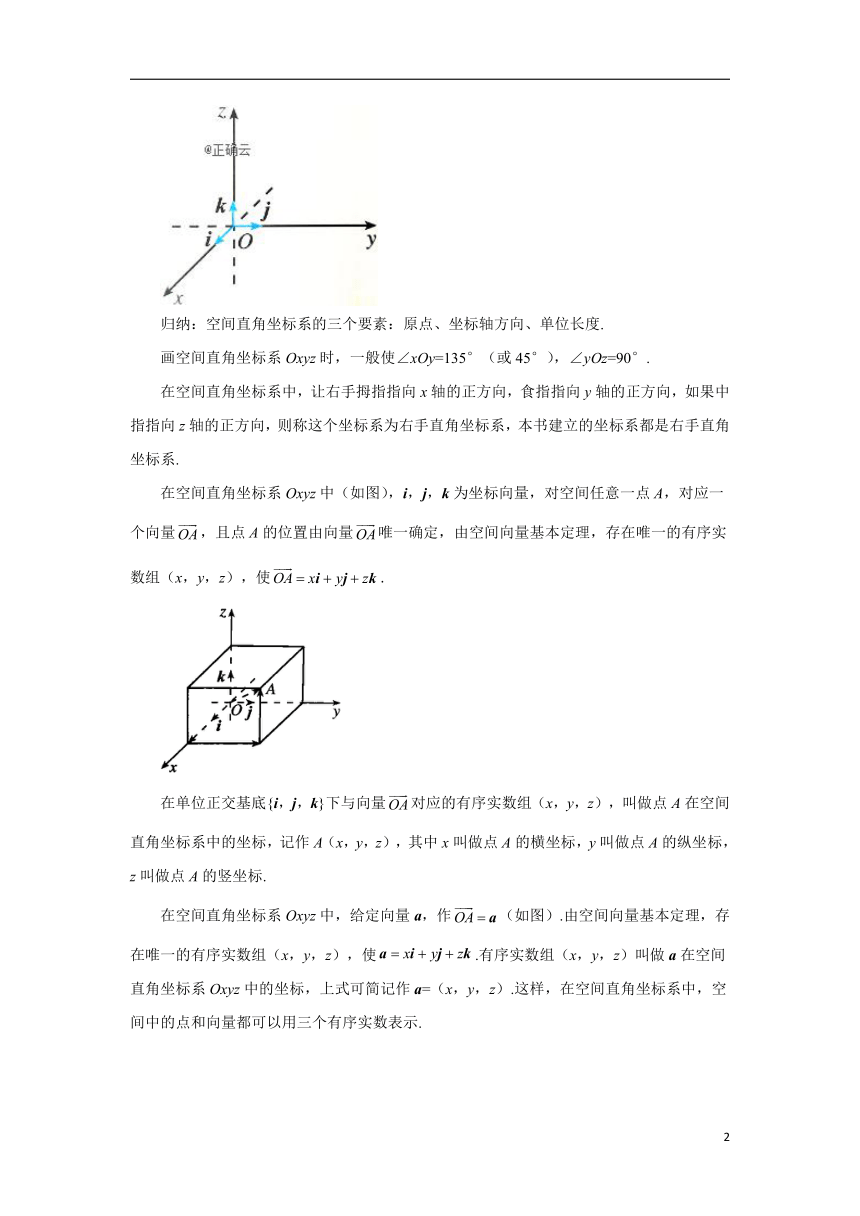
归纳:空间直角坐标系的三个要素:原点、坐标轴方向、单位长度.
画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系,本书建立的坐标系都是右手直角坐标系.
在空间直角坐标系Oxyz中(如图),i,j,k为坐标向量,对空间任意一点A,对应一个向量,且点A的位置由向量唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使.
在单位正交基底{i,j,k}下与向量对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.
在空间直角坐标系Oxyz中,给定向量a,作(如图).由空间向量基本定理,存在唯一的有序实数组(x,y,z),使.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,上式可简记作a=(x,y,z).这样,在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
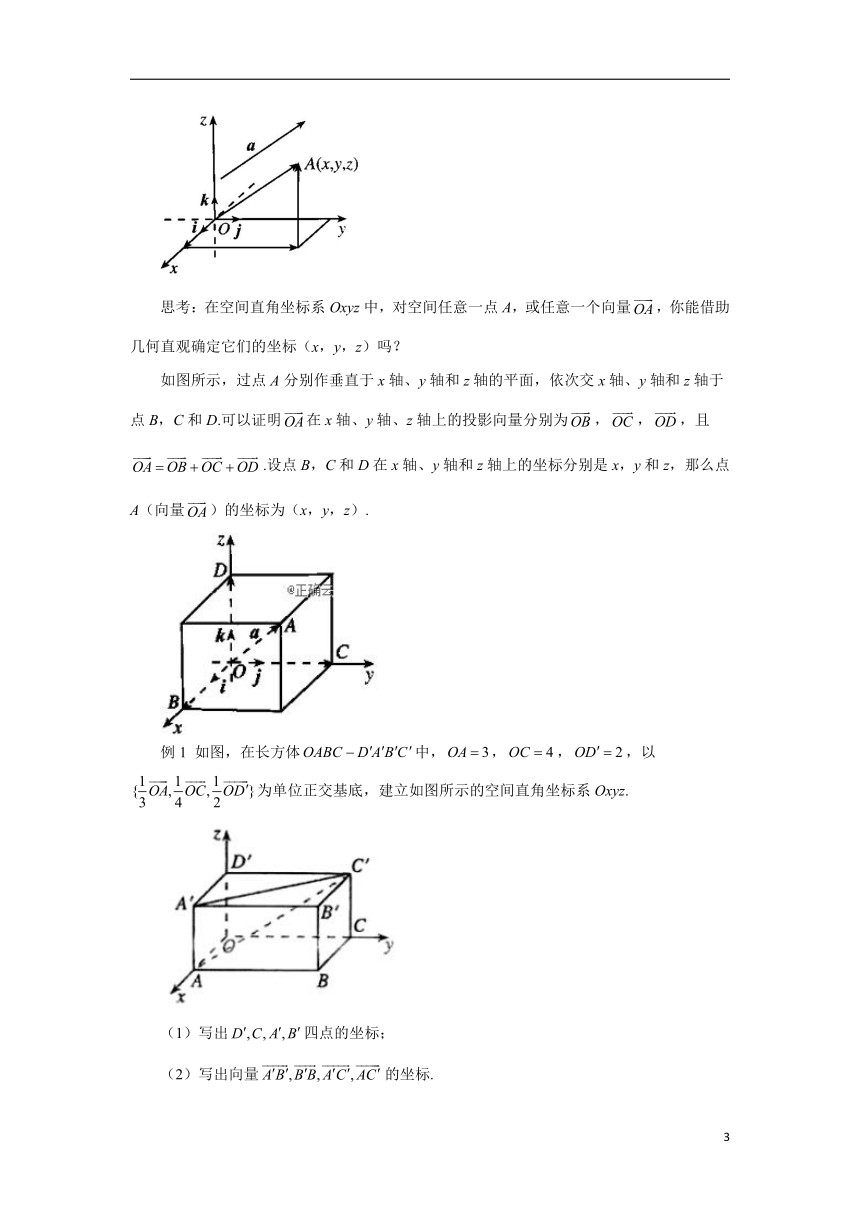
思考:在空间直角坐标系Oxyz中,对空间任意一点A,或任意一个向量,你能借助几何直观确定它们的坐标(x,y,z)吗?
如图所示,过点A分别作垂直于x轴、y轴和z轴的平面,依次交x轴、y轴和z轴于点B,C和D.可以证明在x轴、y轴、z轴上的投影向量分别为,,,且.设点B,C和D在x轴、y轴和z轴上的坐标分别是x,y和z,那么点A(向量)的坐标为(x,y,z).
例1 如图,在长方体中,,,,以为单位正交基底,建立如图所示的空间直角坐标系Oxyz.
(1)写出四点的坐标;
(2)写出向量的坐标.
解:(1)点在z轴上,且,所以.所以点的坐标是.
同理,点C的坐标是.
点在x轴、y轴、z轴上的射影分别为A,O,,它们在坐标轴上的坐标分别为3,0,2,所以点的坐标是.
点在轴、轴、轴上的射影分别为,它们在坐标轴上的坐标分别为3,4,2,所以点的坐标是.
(2);
;
.
(三)课堂练习
1.已知是标准正交基底,且,则的坐标为( )
A. B. C. D.
答案:A
解析:根据空间向量坐标的定义,知,故选A.
2.点在空间直角坐标系中的( )
A.轴上 B.平面内 C.平面内 D.平面内
答案:C
解析:点的纵坐标为0,所以该点在平面内.
3.在空间直角坐标系中,点关于平面对称的点的坐标是( )
A. B. C. D.
答案:A
解析:过点向平面作垂线,垂足为,则就是点与其关于平面对称的点连线的中点.又,所以.
4.在长方体中,若,则向量在基底下的坐标是______________.
答案:
解析:,向量在基底下的坐标是.
5.在长方体中,已知,连接,如图,建立空间直角坐标系.
(1)在图中标出点的位置;
(2)求与的坐标;
(3)求向量在平面上的投影向量的坐标.
答案:(1)点的位置如图中所示:
(2)设分别为方向上的单位向量,
则,
,
所以.
(3)连接,则向量在平面上的投影向量为.
又,
所以.
(四)小结作业
小结:1.空间直角坐标系的建立;
2.空间直角坐标系中点的坐标表示.
作业:
四、板书设计
1.3.1 空间直角坐标系
在空间选定一点O和一个单位正交基底{i,j,k}.以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.
1
1.3 空间向量及其运算的坐标表示
1.3.1 空间直角坐标系
教学设计
一、教学目标
1. 了解空间直角坐标系,会用空间直角坐标系刻画点的位置;
2. 掌握利用坐标表示空间直角坐标系中点的方法.
二、教学重难点
1. 教学重点
空间直角坐标系的建立,空间直角坐标系中点的坐标表示.
2. 教学难点
在空间直角坐标系中画出给定坐标的点的位置.
三、教学过程
(一)新课导入
平面直角坐标系由平面内两条互相垂直、原点重合的数轴组成.如图,在平面内选定一点O和一个单位正交基底{i,j},以O为原点,分别以i,j的方向为正方向、以它们的长为单位长度建立两条数轴:x轴、y轴,那么就建立了一个平面直角坐标系.
类比平面直角坐标系,探究空间直角坐标系.
(二)探索新知
在空间选定一点O和一个单位正交基底{i,j,k}(如图).以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.
归纳:空间直角坐标系的三个要素:原点、坐标轴方向、单位长度.
画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系,本书建立的坐标系都是右手直角坐标系.
在空间直角坐标系Oxyz中(如图),i,j,k为坐标向量,对空间任意一点A,对应一个向量,且点A的位置由向量唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使.
在单位正交基底{i,j,k}下与向量对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.
在空间直角坐标系Oxyz中,给定向量a,作(如图).由空间向量基本定理,存在唯一的有序实数组(x,y,z),使.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,上式可简记作a=(x,y,z).这样,在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
思考:在空间直角坐标系Oxyz中,对空间任意一点A,或任意一个向量,你能借助几何直观确定它们的坐标(x,y,z)吗?
如图所示,过点A分别作垂直于x轴、y轴和z轴的平面,依次交x轴、y轴和z轴于点B,C和D.可以证明在x轴、y轴、z轴上的投影向量分别为,,,且.设点B,C和D在x轴、y轴和z轴上的坐标分别是x,y和z,那么点A(向量)的坐标为(x,y,z).
例1 如图,在长方体中,,,,以为单位正交基底,建立如图所示的空间直角坐标系Oxyz.
(1)写出四点的坐标;
(2)写出向量的坐标.
解:(1)点在z轴上,且,所以.所以点的坐标是.
同理,点C的坐标是.
点在x轴、y轴、z轴上的射影分别为A,O,,它们在坐标轴上的坐标分别为3,0,2,所以点的坐标是.
点在轴、轴、轴上的射影分别为,它们在坐标轴上的坐标分别为3,4,2,所以点的坐标是.
(2);
;
.
(三)课堂练习
1.已知是标准正交基底,且,则的坐标为( )
A. B. C. D.
答案:A
解析:根据空间向量坐标的定义,知,故选A.
2.点在空间直角坐标系中的( )
A.轴上 B.平面内 C.平面内 D.平面内
答案:C
解析:点的纵坐标为0,所以该点在平面内.
3.在空间直角坐标系中,点关于平面对称的点的坐标是( )
A. B. C. D.
答案:A
解析:过点向平面作垂线,垂足为,则就是点与其关于平面对称的点连线的中点.又,所以.
4.在长方体中,若,则向量在基底下的坐标是______________.
答案:
解析:,向量在基底下的坐标是.
5.在长方体中,已知,连接,如图,建立空间直角坐标系.
(1)在图中标出点的位置;
(2)求与的坐标;
(3)求向量在平面上的投影向量的坐标.
答案:(1)点的位置如图中所示:
(2)设分别为方向上的单位向量,
则,
,
所以.
(3)连接,则向量在平面上的投影向量为.
又,
所以.
(四)小结作业
小结:1.空间直角坐标系的建立;
2.空间直角坐标系中点的坐标表示.
作业:
四、板书设计
1.3.1 空间直角坐标系
在空间选定一点O和一个单位正交基底{i,j,k}.以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.
1
