2021-2022学年新教材人教A版选择性必修第一册 1.3.2空间向量运算的坐标表示 教案
文档属性
| 名称 | 2021-2022学年新教材人教A版选择性必修第一册 1.3.2空间向量运算的坐标表示 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 434.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 00:00:00 | ||
图片预览

文档简介
第一章空间向量与立体几何
1.3.2空间向量运算的坐标表示
教学设计
一、教学目标
1.掌握空间向量坐标运算公式,并能解决简单几何问题.
2.能熟练应用两个向量夹角与向量长度的坐标计算公式.
3.掌握平行向量、垂直向量的坐标表示,并能解决相关的向量的平行、向量的垂直问题.
二、教学重难点
1、教学重点
空间向量的坐标运算,夹角公式,距离公式,空间向量平行和垂直的条件.
2、教学难点
空间向量的平行、垂直、夹角、距离问题.
三、教学过程
1、新课导入
上节课我们学习了空间向量的坐标表示,你能类比平面向量的坐标运算,得出空间向量运算的坐标表示并给出证明吗?
2、探索新知
一、空间向量运算的坐标表示:
设,,则
,
,
,,
.
二、空间向量数量积运算的坐标表示的证明:
设为空间的一个单位正交基底,则,,所以,利用向量数量积的分配律以及,,得.
三、空间向量的平行、垂直、长度和夹角余弦的坐标表示:
当时,,,;
;
;
.
四、空间两点间的距离公式:
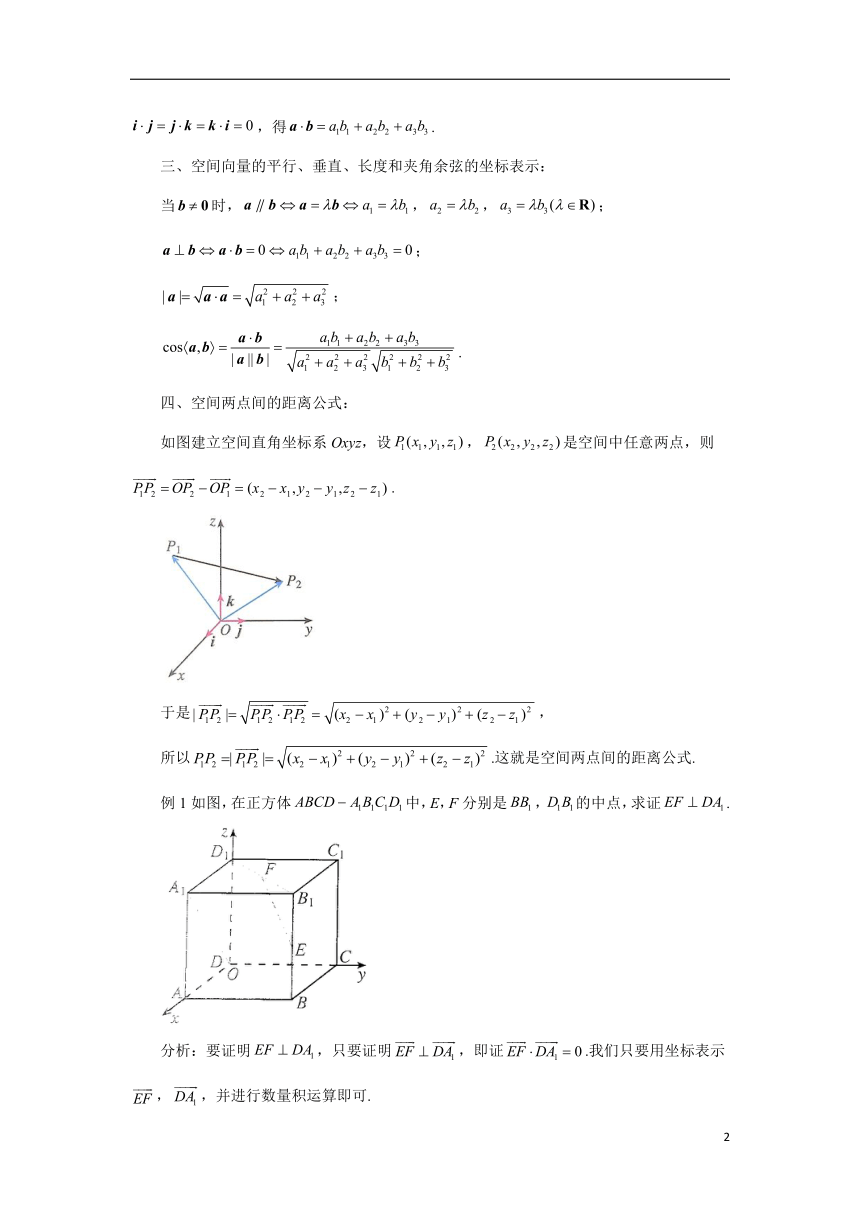
如图建立空间直角坐标系Oxyz,设,是空间中任意两点,则.
于是,
所以.这就是空间两点间的距离公式.
例1如图,在正方体中,E,F分别是,的中点,求证.
分析:要证明,只要证明,即证.我们只要用坐标表示,,并进行数量积运算即可.
证明:不妨设正方体的棱长为1,建立如图所示的空间直角坐标系Oxyz,则,,所以.
又,,所以.
所以,
所以,即.
例2 如图,在棱长为1的正方体中,M为的中点,分别在棱,上,,.
(1)求AM的长
(2)求与所成角的余弦值.
分析:(1)利用条件建立适当的空间直角坐标系,写出点A,M的坐标,利用空间两点间的距离公式求出AM的长.(2)与所成的角就是,所成的角或它的补角,因此,可以通过,的坐标运算得到结果.
解:(1)建立如图所示的空间直角坐标系Oxyz,则点A的坐标为,点M的坐标为,于是.
(2)由已知,得,,,,
所以,,
,,
所以,
所以.
所以,与所成角的余弦值是.
3、课堂练习
1.向量,,若,且,则的值为( )
A.-1 B.1 C.-4 D.4
2.设向量,,且,则的值为________.
3.如图,在直三棱柱中,,,,M,N分别是,的中点.
(1)求的模;
(2)求的值;
(3)求证:.
4、小结作业
小结:本节课学习了空间向量的坐标运算,平行、垂直、长度和夹角余弦的坐标表示及空间两点间的距离公式.
作业:完成本节课课后习题.
四、板书设计
1.3.2空间向量运算的坐标表示
1.空间向量运算的坐标表示:设,,则
,
,
,,
.
2.空间向量的平行、垂直、长度和夹角余弦的坐标表示:
当时,,,;
;
;
.
3.空间两点间的距离公式:设,是空间中任意两点,则.
1
1.3.2空间向量运算的坐标表示
教学设计
一、教学目标
1.掌握空间向量坐标运算公式,并能解决简单几何问题.
2.能熟练应用两个向量夹角与向量长度的坐标计算公式.
3.掌握平行向量、垂直向量的坐标表示,并能解决相关的向量的平行、向量的垂直问题.
二、教学重难点
1、教学重点
空间向量的坐标运算,夹角公式,距离公式,空间向量平行和垂直的条件.
2、教学难点
空间向量的平行、垂直、夹角、距离问题.
三、教学过程
1、新课导入
上节课我们学习了空间向量的坐标表示,你能类比平面向量的坐标运算,得出空间向量运算的坐标表示并给出证明吗?
2、探索新知
一、空间向量运算的坐标表示:
设,,则
,
,
,,
.
二、空间向量数量积运算的坐标表示的证明:
设为空间的一个单位正交基底,则,,所以,利用向量数量积的分配律以及,,得.
三、空间向量的平行、垂直、长度和夹角余弦的坐标表示:
当时,,,;
;
;
.
四、空间两点间的距离公式:
如图建立空间直角坐标系Oxyz,设,是空间中任意两点,则.
于是,
所以.这就是空间两点间的距离公式.
例1如图,在正方体中,E,F分别是,的中点,求证.
分析:要证明,只要证明,即证.我们只要用坐标表示,,并进行数量积运算即可.
证明:不妨设正方体的棱长为1,建立如图所示的空间直角坐标系Oxyz,则,,所以.
又,,所以.
所以,
所以,即.
例2 如图,在棱长为1的正方体中,M为的中点,分别在棱,上,,.
(1)求AM的长
(2)求与所成角的余弦值.
分析:(1)利用条件建立适当的空间直角坐标系,写出点A,M的坐标,利用空间两点间的距离公式求出AM的长.(2)与所成的角就是,所成的角或它的补角,因此,可以通过,的坐标运算得到结果.
解:(1)建立如图所示的空间直角坐标系Oxyz,则点A的坐标为,点M的坐标为,于是.
(2)由已知,得,,,,
所以,,
,,
所以,
所以.
所以,与所成角的余弦值是.
3、课堂练习
1.向量,,若,且,则的值为( )
A.-1 B.1 C.-4 D.4
2.设向量,,且,则的值为________.
3.如图,在直三棱柱中,,,,M,N分别是,的中点.
(1)求的模;
(2)求的值;
(3)求证:.
4、小结作业
小结:本节课学习了空间向量的坐标运算,平行、垂直、长度和夹角余弦的坐标表示及空间两点间的距离公式.
作业:完成本节课课后习题.
四、板书设计
1.3.2空间向量运算的坐标表示
1.空间向量运算的坐标表示:设,,则
,
,
,,
.
2.空间向量的平行、垂直、长度和夹角余弦的坐标表示:
当时,,,;
;
;
.
3.空间两点间的距离公式:设,是空间中任意两点,则.
1
