2021-2022学年新教材人教A版选择性必修第一册 1.4.1用空间向量研究直线、平面的位置关系 教案
文档属性
| 名称 | 2021-2022学年新教材人教A版选择性必修第一册 1.4.1用空间向量研究直线、平面的位置关系 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 13:20:47 | ||
图片预览



文档简介
第一章空间向量与立体几何
1.4.1用空间向量研究直线、平面的位置关系
教学设计
一、教学目标
1.能用向量语言描述点、直线和平面,理解直线的方向向量和平面的法向量.
2.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直与平行关系,
3.能用向量方法证明有关直线、平面位置关系的判定定理.
二、教学重难点
1、教学重点
理解直线的方向向量和平面的法向量,并会用直线的方向向量和平面的法向量证明直线与平面的位置关系.
2、教学难点
证明有关直线、平面位置关系的判定定理.
三、教学过程
1、新课导入
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题.
2、探索新知
一、空间中点、直线和平面的向量表示
1.空间中点的向量表示:如图,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示.我们把向量称为点P的位置向量.
2.空间中直线的向量表示:如图,a是直线l的方向向量,在直线l上取,设P是直线l上的任意一点,由向量共线的条件可知,点P在直线l上的充要条件是存在实数t,使得,即.
空间直线的向量表示式:如图,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使①,将代人①式,得②,①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
3.空间中平面的向量表示:平面可以由内两条相交直线确定.如图,设两条直线相交于点O,它们的方向向量分别为a和b,P为平面内任意一点,由平面向量基本定理可知存在唯一的有序实数对,使得.
这样,点O与向量a,b不仅可以确定平面,还可以具体表示出内的任意一点.
空间平面的向量表示式:如图,取定空间任意一点O,可以得到,空间一点P位于平面ABC内的充要条件是存在实数x,使③.我们把③式称为空间平面ABC的向量表示式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
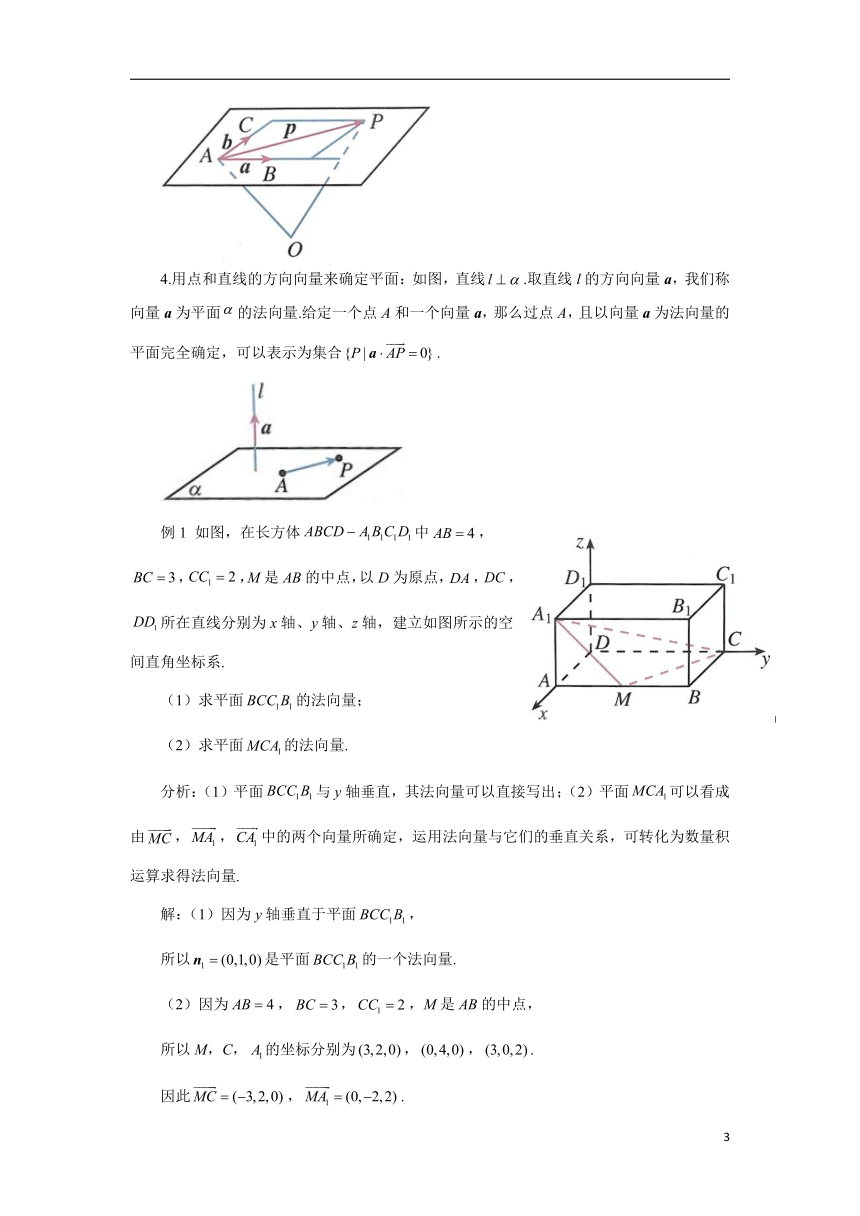
4.用点和直线的方向向量来确定平面:如图,直线.取直线l的方向向量a,我们称向量a为平面的法向量.给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合.
例1 如图,在长方体中,,,M是AB的中点,以D为原点,,,所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求平面的法向量;
(2)求平面的法向量.
分析:(1)平面与y轴垂直,其法向量可以直接写出;(2)平面可以看成由,,中的两个向量所确定,运用法向量与它们的垂直关系,可转化为数量积运算求得法向量.
解:(1)因为y轴垂直于平面,
所以是平面的一个法向量.
(2)因为,,,M是AB的中点,
所以M,C,的坐标分别为,,.
因此,.
设是平面的法向量,则,.
所以,
所以,取,则,.
于是是平面的一个法向量.
二、空间中直线、平面的平行
如图,设,分别是直线,的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行,所以,使得.
如图,设u是直线l的方向向量,n是平面的法向量,,则.
如图,设,分别是平面,的法向量,则,使得.
例2证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,,,,,.求证:.
证明:如图,取平面的法向量n,直线a,b的方向向量u,v.
因为,,所以,.
因为,,,
所以对任意点,存在,使得.
从而.
所以,向量n也是平面的法向量.故.
例3如图,在长方体中,,,.线段上是否存在点P,使得平面?
证明:以D为原点,,,所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
因为A,C,的坐标分别为,,,
所以,.
设是平面的法向量,则,,
即,所以.取,则,.
所以是平面的一个法向量.
由,,的坐标分别为,,,
得,.
设点P满足,则,
所以.
令,得,解得,这样的点P存在.
所以,当,即P为的中点时,平面.
三、空间中直线、平面的垂直
一般地,直线与直线垂直,就是两直线的方向向量垂直;直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
如图(1),设直线,的方向向量分别为,,则.
如图(2),设直线l的方向向量为u,平面的法向量为n,则,使得.
如图(3),设平面,的法向量分别为,,则.
例4如图,在平行六面体中,,,求证:直线平面.
证明:设,,,则为空间的一个基底,
且,,.
因为,,
所以,.
在平面上,取,为基向量,
则对于平面上任意一点P,存在唯一的有序实数对,使得.
所以.
所以是平面的法向量.
所以平面.
例5证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,,,求证:.
证明:取直线l的方向向量u,平面的法向量n.
因为,所以u是平面的法向量.
因为,而n是平面的法向量,所以.
所以.
3、课堂练习
1.对于空间任意一点和不共线的三点A,B,C,有,则( )
A.O,A,B,C四点必共面 B.P,A,B,C四点必共面
C.O,P,B,C四点必共面 D.O,P,A,B,C五点必共面
2.已知点是平行四边形所在的平面外一点,如果,,.对于结论:①;②;③是平面的法向量;④.其中正确的是________________.
3.如图,在四棱锥中,底面,与底面所成的角为45°,底面为直角梯形,,.问在棱上是否存在一点,使得平面 若存在,求出点E的位置;若不存在,请说明理由.
4、小结作业
小结:本节课学习了空间中点、直线和平面的向量表示,用向量刻画空间中直线、平面的平行、垂直关系.
作业:完成本节课课后习题.
四、板书设计
1.4.1用空间向量研究直线、平面的位置关系
1.空间直线的向量表示式:取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使①,将代人①式,得②,①式和②式都称为空间直线的向量表示式. 由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
2.空间平面的向量表示式:取定空间任意一点O,可以得到,空间一点P位于平面ABC内的充要条件是存在实数x,使③. 我们把③式称为空间平面ABC的向量表示式. 由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
3.空间中直线、平面的平行:
①直线与直线平行:设,分别是直线,的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行,所以,使得.
②直线与平面平行:设u是直线l的方向向量,n是平面的法向量,,则.
③平面与平面平行:设,分别是平面,的法向量,则,使得.
4.空间中直线、平面的垂直:
①直线与直线垂直:设直线,的方向向量分别为,,则.
②直线与平面垂直:直线l的方向向量为u,平面的法向量为n,则,使得.
③平面与平面垂直:设平面,的法向量分别为,,则.
1
1.4.1用空间向量研究直线、平面的位置关系
教学设计
一、教学目标
1.能用向量语言描述点、直线和平面,理解直线的方向向量和平面的法向量.
2.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直与平行关系,
3.能用向量方法证明有关直线、平面位置关系的判定定理.
二、教学重难点
1、教学重点
理解直线的方向向量和平面的法向量,并会用直线的方向向量和平面的法向量证明直线与平面的位置关系.
2、教学难点
证明有关直线、平面位置关系的判定定理.
三、教学过程
1、新课导入
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、平面的位置关系和度量问题.
2、探索新知
一、空间中点、直线和平面的向量表示
1.空间中点的向量表示:如图,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示.我们把向量称为点P的位置向量.
2.空间中直线的向量表示:如图,a是直线l的方向向量,在直线l上取,设P是直线l上的任意一点,由向量共线的条件可知,点P在直线l上的充要条件是存在实数t,使得,即.
空间直线的向量表示式:如图,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使①,将代人①式,得②,①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
3.空间中平面的向量表示:平面可以由内两条相交直线确定.如图,设两条直线相交于点O,它们的方向向量分别为a和b,P为平面内任意一点,由平面向量基本定理可知存在唯一的有序实数对,使得.
这样,点O与向量a,b不仅可以确定平面,还可以具体表示出内的任意一点.
空间平面的向量表示式:如图,取定空间任意一点O,可以得到,空间一点P位于平面ABC内的充要条件是存在实数x,使③.我们把③式称为空间平面ABC的向量表示式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
4.用点和直线的方向向量来确定平面:如图,直线.取直线l的方向向量a,我们称向量a为平面的法向量.给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合.
例1 如图,在长方体中,,,M是AB的中点,以D为原点,,,所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求平面的法向量;
(2)求平面的法向量.
分析:(1)平面与y轴垂直,其法向量可以直接写出;(2)平面可以看成由,,中的两个向量所确定,运用法向量与它们的垂直关系,可转化为数量积运算求得法向量.
解:(1)因为y轴垂直于平面,
所以是平面的一个法向量.
(2)因为,,,M是AB的中点,
所以M,C,的坐标分别为,,.
因此,.
设是平面的法向量,则,.
所以,
所以,取,则,.
于是是平面的一个法向量.
二、空间中直线、平面的平行
如图,设,分别是直线,的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行,所以,使得.
如图,设u是直线l的方向向量,n是平面的法向量,,则.
如图,设,分别是平面,的法向量,则,使得.
例2证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,,,,,.求证:.
证明:如图,取平面的法向量n,直线a,b的方向向量u,v.
因为,,所以,.
因为,,,
所以对任意点,存在,使得.
从而.
所以,向量n也是平面的法向量.故.
例3如图,在长方体中,,,.线段上是否存在点P,使得平面?
证明:以D为原点,,,所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
因为A,C,的坐标分别为,,,
所以,.
设是平面的法向量,则,,
即,所以.取,则,.
所以是平面的一个法向量.
由,,的坐标分别为,,,
得,.
设点P满足,则,
所以.
令,得,解得,这样的点P存在.
所以,当,即P为的中点时,平面.
三、空间中直线、平面的垂直
一般地,直线与直线垂直,就是两直线的方向向量垂直;直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
如图(1),设直线,的方向向量分别为,,则.
如图(2),设直线l的方向向量为u,平面的法向量为n,则,使得.
如图(3),设平面,的法向量分别为,,则.
例4如图,在平行六面体中,,,求证:直线平面.
证明:设,,,则为空间的一个基底,
且,,.
因为,,
所以,.
在平面上,取,为基向量,
则对于平面上任意一点P,存在唯一的有序实数对,使得.
所以.
所以是平面的法向量.
所以平面.
例5证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,,,求证:.
证明:取直线l的方向向量u,平面的法向量n.
因为,所以u是平面的法向量.
因为,而n是平面的法向量,所以.
所以.
3、课堂练习
1.对于空间任意一点和不共线的三点A,B,C,有,则( )
A.O,A,B,C四点必共面 B.P,A,B,C四点必共面
C.O,P,B,C四点必共面 D.O,P,A,B,C五点必共面
2.已知点是平行四边形所在的平面外一点,如果,,.对于结论:①;②;③是平面的法向量;④.其中正确的是________________.
3.如图,在四棱锥中,底面,与底面所成的角为45°,底面为直角梯形,,.问在棱上是否存在一点,使得平面 若存在,求出点E的位置;若不存在,请说明理由.
4、小结作业
小结:本节课学习了空间中点、直线和平面的向量表示,用向量刻画空间中直线、平面的平行、垂直关系.
作业:完成本节课课后习题.
四、板书设计
1.4.1用空间向量研究直线、平面的位置关系
1.空间直线的向量表示式:取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使①,将代人①式,得②,①式和②式都称为空间直线的向量表示式. 由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
2.空间平面的向量表示式:取定空间任意一点O,可以得到,空间一点P位于平面ABC内的充要条件是存在实数x,使③. 我们把③式称为空间平面ABC的向量表示式. 由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
3.空间中直线、平面的平行:
①直线与直线平行:设,分别是直线,的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行,所以,使得.
②直线与平面平行:设u是直线l的方向向量,n是平面的法向量,,则.
③平面与平面平行:设,分别是平面,的法向量,则,使得.
4.空间中直线、平面的垂直:
①直线与直线垂直:设直线,的方向向量分别为,,则.
②直线与平面垂直:直线l的方向向量为u,平面的法向量为n,则,使得.
③平面与平面垂直:设平面,的法向量分别为,,则.
1
