新教材人教A版选择性必修第一册 2.1.2两条直线平行和垂直的判定 教案
文档属性
| 名称 | 新教材人教A版选择性必修第一册 2.1.2两条直线平行和垂直的判定 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 00:00:00 | ||
图片预览

文档简介
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.2 两条直线平行和垂直的判定
教学设计
一、教学目标
1. 掌握两条直线平行与垂直的条件;
2. 能根据斜率判定两条直线平行或垂直.
二、教学重难点
1. 教学重点
两直线平行与垂直的判定及其应用.
2. 教学难点
探究两条直线斜率与两条直线垂直的关系.
三、教学过程
(一)新课导入
问题1:平面中两条直线有几种位置关系?
两种,相交和平行.
问题2:斜率是刻画直线倾斜程度的量,当两条直线相互平行或相互垂直时,它们之间的斜率有何关系?
(二)探索新知
如图,若,则与的倾斜角与相等,由,可得,即.因此,若,则.反之,当时,,由倾斜角的取值范围及正切函数的单调性可知,,因此.
于是,对于斜率分别为,的两条直线,,有.
显然,当时,直线的斜率不存在,此时.
若直线,重合,此时仍然有.用斜率证明三点共线时,常常用到这个结论.
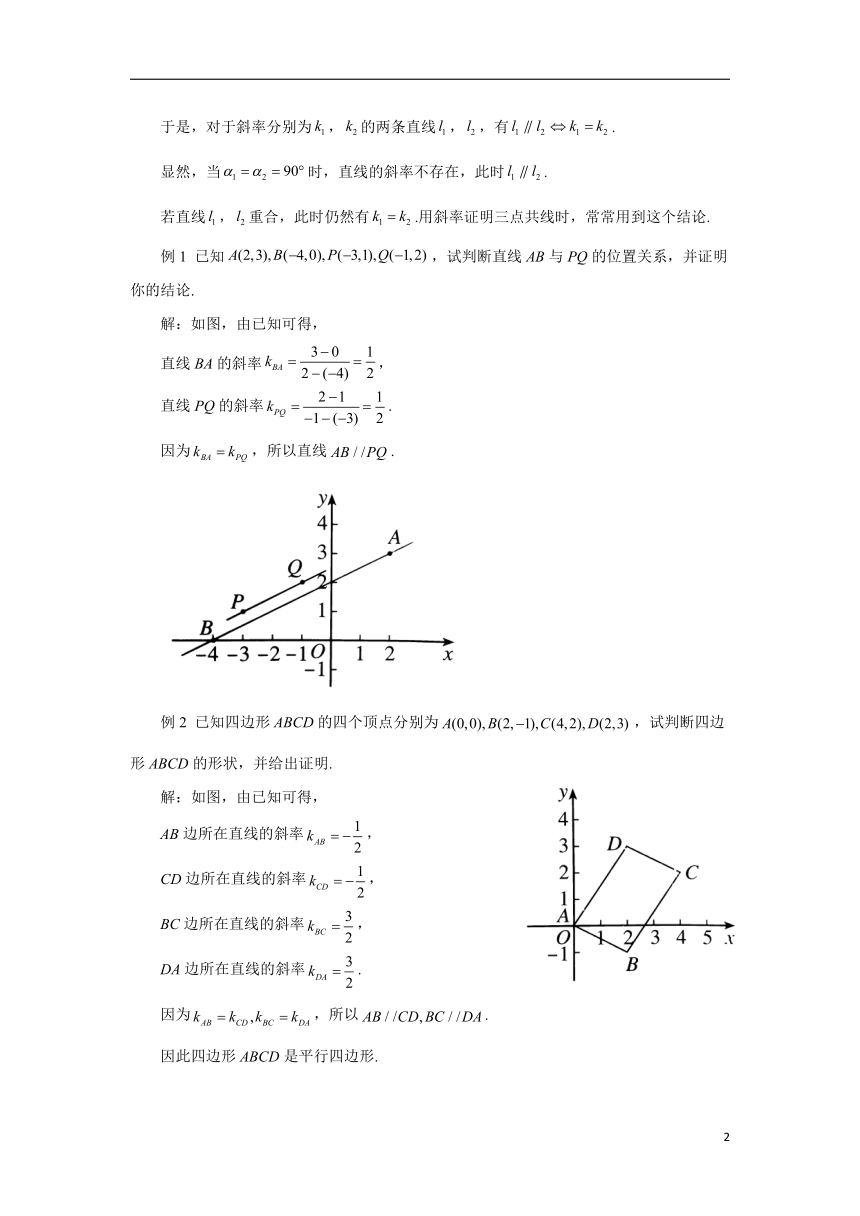
例1 已知,试判断直线AB与PQ的位置关系,并证明你的结论.
解:如图,由已知可得,
直线BA的斜率,
直线PQ的斜率.
因为,所以直线.
例2 已知四边形ABCD的四个顶点分别为,试判断四边形ABCD的形状,并给出证明.
解:如图,由已知可得,
AB边所在直线的斜率,
CD边所在直线的斜率,
BC边所在直线的斜率,
DA边所在直线的斜率.
因为,所以.
因此四边形ABCD是平行四边形.
显然,当两条直线相交时,它们的斜率不相等;反之,当两条直线的斜率不相等时,它们相交.在相交的位置关系中,垂直是最特殊的情形.
思考:当直线,垂直时,它们的斜率有什么数量关系?
设两条直线,的斜率分别为,,则直线,的方向向量分别是,,于是,即.
也就是说,.
当直线或的倾斜角为90°时,若,则另一条直线的倾斜角为0°;反之亦然.
由上得到,如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果两条直线的斜率之积等于-1,那么它们互相垂直.即.
例3 已知,试判断直线AB与PQ的位置关系.
解:直线AB的斜率,
直线PQ的斜率.
因为,所以直线.
例4 已知三点,试判断的形状.
解:边AB所在直线的斜率,边BC所在直线的斜率.
由,得,即.
所以是直角三角形.
(三)课堂练习
1.下列结论错误的是( )
A.若直线的斜率相等,则
B.若直线的斜率,则
C.若直线的斜率都不存在,则
D.若直线的斜率不相等,则与不平行
答案:ABC
解析:若直线的斜率相等,则或与重合,所以A结论错误;若直线的斜率,则,所以B结论错误;若直线的斜率都不存在,则或与重合,所以C结论错误;D结论正确.故选ABC.
2.若直线的倾斜角为135°,直线经过点,,则直线与的位置关系是( )
A.垂直 B.平行 C.重合 D.平行或重合
答案:D
解析:由题意得,直线的斜率为,直线的斜率为,直线与平行或重合.
3.若直线l经过点和,且与斜率为的直线垂直,则实数a的值是( )
A. B. C. D.
答案:A
解析:依题意得,,即,解得,故选A.
4.若不同两点P,Q的坐标分别为,,则线段PQ的垂直平分线的斜率为_________________.
答案:-1
解析:由题意得,所以线段PQ的垂直平分线的斜率为-1.
5.已知平行四边形中,.
(1)求点的坐标;
(2)试判断平行四边形是否为菱形.
答案:(1)设,则,
即,解得,
所以.
(2)因为,
所以,所以,
故平行四边形为菱形.
(四)小结作业
小结:根据斜率判定两条直线平行或垂直.
作业:
四、板书设计
2.1.2 两条直线平行和垂直的判定
对于斜率分别为,的两条直线,,有
(1);
(2).
1
2.1 直线的倾斜角与斜率
2.1.2 两条直线平行和垂直的判定
教学设计
一、教学目标
1. 掌握两条直线平行与垂直的条件;
2. 能根据斜率判定两条直线平行或垂直.
二、教学重难点
1. 教学重点
两直线平行与垂直的判定及其应用.
2. 教学难点
探究两条直线斜率与两条直线垂直的关系.
三、教学过程
(一)新课导入
问题1:平面中两条直线有几种位置关系?
两种,相交和平行.
问题2:斜率是刻画直线倾斜程度的量,当两条直线相互平行或相互垂直时,它们之间的斜率有何关系?
(二)探索新知
如图,若,则与的倾斜角与相等,由,可得,即.因此,若,则.反之,当时,,由倾斜角的取值范围及正切函数的单调性可知,,因此.
于是,对于斜率分别为,的两条直线,,有.
显然,当时,直线的斜率不存在,此时.
若直线,重合,此时仍然有.用斜率证明三点共线时,常常用到这个结论.
例1 已知,试判断直线AB与PQ的位置关系,并证明你的结论.
解:如图,由已知可得,
直线BA的斜率,
直线PQ的斜率.
因为,所以直线.
例2 已知四边形ABCD的四个顶点分别为,试判断四边形ABCD的形状,并给出证明.
解:如图,由已知可得,
AB边所在直线的斜率,
CD边所在直线的斜率,
BC边所在直线的斜率,
DA边所在直线的斜率.
因为,所以.
因此四边形ABCD是平行四边形.
显然,当两条直线相交时,它们的斜率不相等;反之,当两条直线的斜率不相等时,它们相交.在相交的位置关系中,垂直是最特殊的情形.
思考:当直线,垂直时,它们的斜率有什么数量关系?
设两条直线,的斜率分别为,,则直线,的方向向量分别是,,于是,即.
也就是说,.
当直线或的倾斜角为90°时,若,则另一条直线的倾斜角为0°;反之亦然.
由上得到,如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果两条直线的斜率之积等于-1,那么它们互相垂直.即.
例3 已知,试判断直线AB与PQ的位置关系.
解:直线AB的斜率,
直线PQ的斜率.
因为,所以直线.
例4 已知三点,试判断的形状.
解:边AB所在直线的斜率,边BC所在直线的斜率.
由,得,即.
所以是直角三角形.
(三)课堂练习
1.下列结论错误的是( )
A.若直线的斜率相等,则
B.若直线的斜率,则
C.若直线的斜率都不存在,则
D.若直线的斜率不相等,则与不平行
答案:ABC
解析:若直线的斜率相等,则或与重合,所以A结论错误;若直线的斜率,则,所以B结论错误;若直线的斜率都不存在,则或与重合,所以C结论错误;D结论正确.故选ABC.
2.若直线的倾斜角为135°,直线经过点,,则直线与的位置关系是( )
A.垂直 B.平行 C.重合 D.平行或重合
答案:D
解析:由题意得,直线的斜率为,直线的斜率为,直线与平行或重合.
3.若直线l经过点和,且与斜率为的直线垂直,则实数a的值是( )
A. B. C. D.
答案:A
解析:依题意得,,即,解得,故选A.
4.若不同两点P,Q的坐标分别为,,则线段PQ的垂直平分线的斜率为_________________.
答案:-1
解析:由题意得,所以线段PQ的垂直平分线的斜率为-1.
5.已知平行四边形中,.
(1)求点的坐标;
(2)试判断平行四边形是否为菱形.
答案:(1)设,则,
即,解得,
所以.
(2)因为,
所以,所以,
故平行四边形为菱形.
(四)小结作业
小结:根据斜率判定两条直线平行或垂直.
作业:
四、板书设计
2.1.2 两条直线平行和垂直的判定
对于斜率分别为,的两条直线,,有
(1);
(2).
1
