5.2运动的合成和分解 同步练习(含答案)
文档属性
| 名称 | 5.2运动的合成和分解 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 316.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-21 00:00:00 | ||
图片预览



文档简介
5.2运动的合成和分解
、单选题
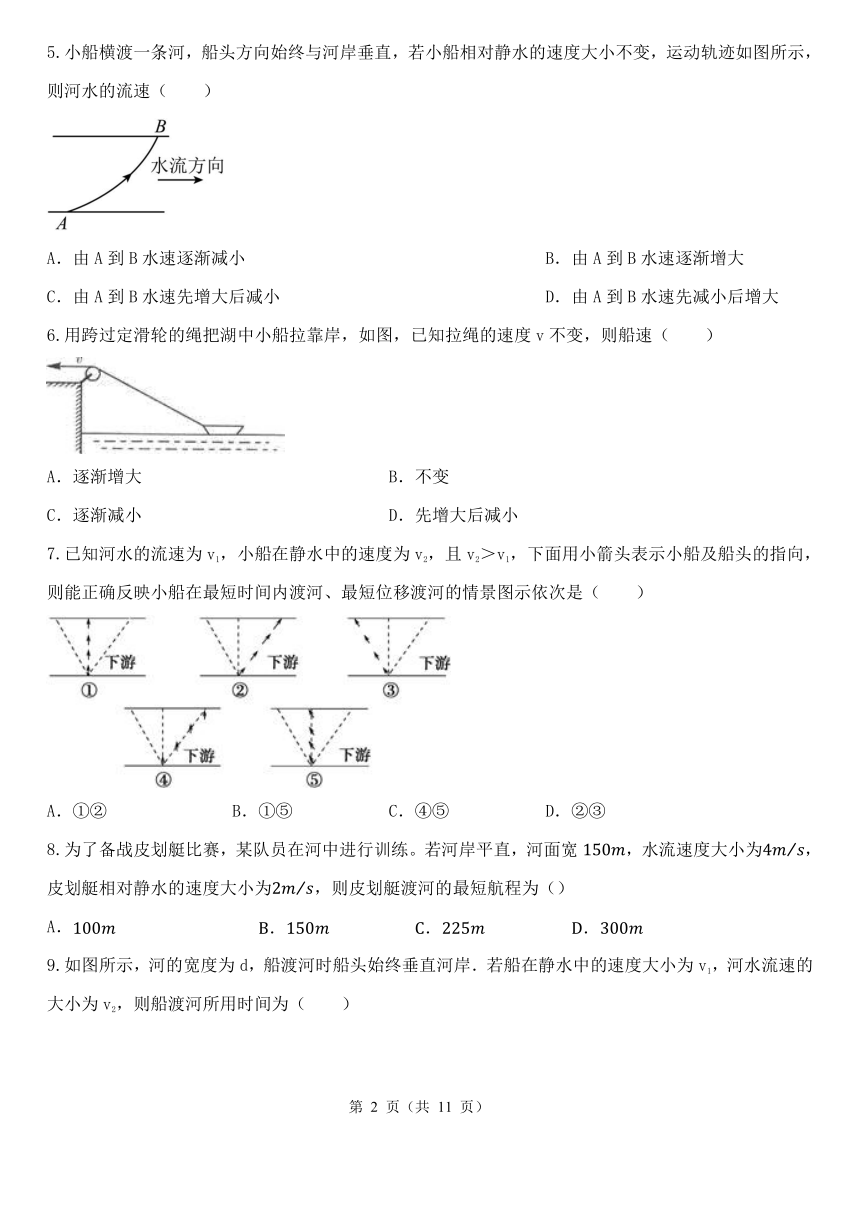
光滑水平面上有一直角坐标系,质量m=4 kg的质点静止在坐标原点O处.先用沿x轴正方向的力F1=8 N作用了2 s;然后撤去F1,并立即用沿y轴正方向的力F2=24 N作用1 s,则质点在这3 s内的轨迹为图中的( ).
A. B.
C. D.
有一条两岸平直、河水均匀流动,流速恒为v的大河,一条小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直,小船在静水中的速度大小为2v,去程与回程所用时间之比为( )
A.3∶2 B.2∶1 C.3∶1 D.
一只小船在静水中的速度为4m/s,它要渡过40m宽的河,河水的速度为3m/s,则下列说法正确的是( )
A.船不能渡过河 B.船不能垂直到达对岸
C.船渡河的最短时间为10s D.船渡河的速度一定为5m/s
一质点同时参与相互垂直的x方向和y方向上的两个运动,已知t=0时刻,x方向上速度为3m/s,y方向上速度为4m/s;两个方向上的运动均为匀加速运动,x方向上的加速度为4m/s2,y方向上的加速度为3m/s2.下列哪个图能定性描述该质点的运动轨迹( )
A. B.
C. D.
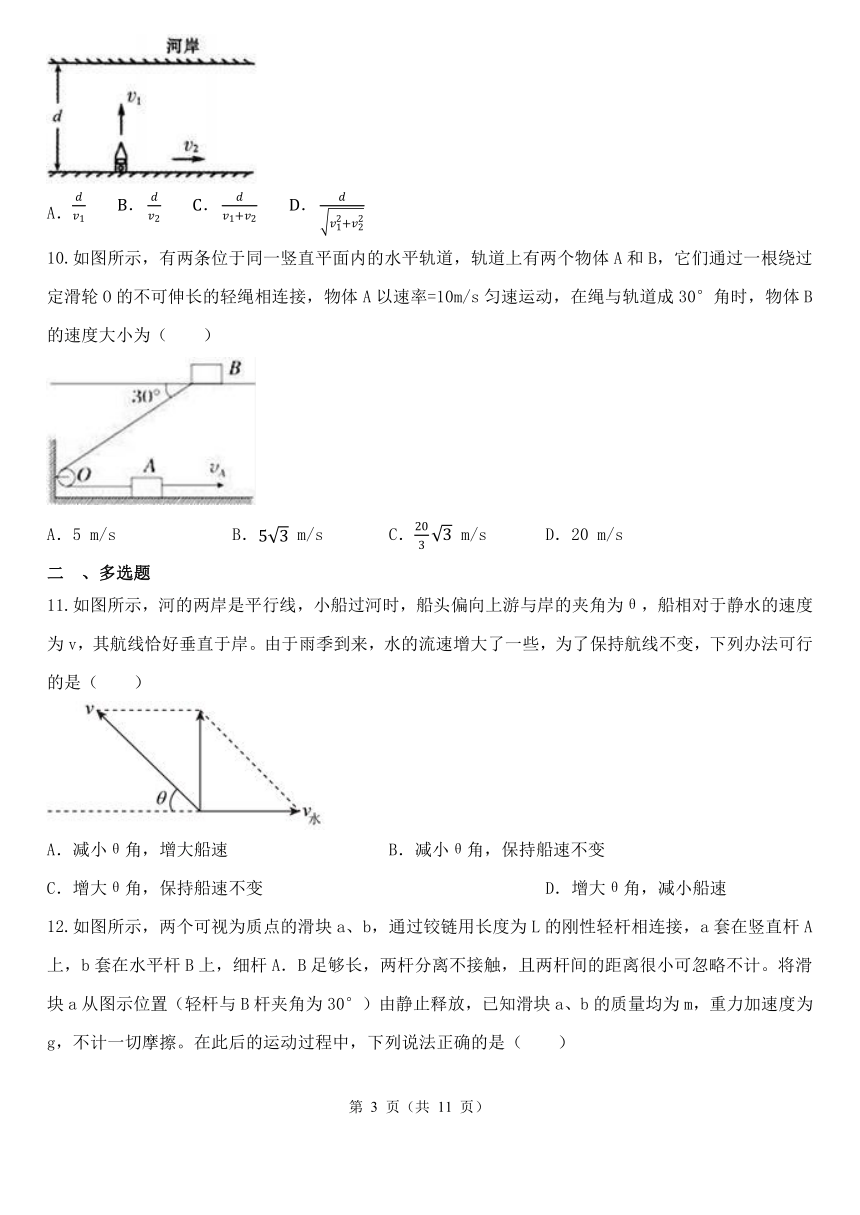
小船横渡一条河,船头方向始终与河岸垂直,若小船相对静水的速度大小不变,运动轨迹如图所示,则河水的流速( )
A.由A到B水速逐渐减小 B.由A到B水速逐渐增大
C.由A到B水速先增大后减小 D.由A到B水速先减小后增大
用跨过定滑轮的绳把湖中小船拉靠岸,如图,已知拉绳的速度v不变,则船速( )
A.逐渐增大 B.不变
C.逐渐减小 D.先增大后减小
已知河水的流速为v1,小船在静水中的速度为v2,且v2>v1,下面用小箭头表示小船及船头的指向,则能正确反映小船在最短时间内渡河、最短位移渡河的情景图示依次是( )
A.①② B.①⑤ C.④⑤ D.②③
为了备战皮划艇比赛,某队员在河中进行训练。若河岸平直,河面宽,水流速度大小为,皮划艇相对静水的速度大小为,则皮划艇渡河的最短航程为()
A.
如图所示,河的宽度为d,船渡河时船头始终垂直河岸.若船在静水中的速度大小为v1,河水流速的大小为v2,则船渡河所用时间为( )
A.
如图所示,有两条位于同一竖直平面内的水平轨道,轨道上有两个物体A和B,它们通过一根绕过定滑轮O的不可伸长的轻绳相连接,物体A以速率=10m/s匀速运动,在绳与轨道成30°角时,物体B的速度大小为( )
A.5 m/s B. m/s C. m/s D.20 m/s
、多选题
如图所示,河的两岸是平行线,小船过河时,船头偏向上游与岸的夹角为θ,船相对于静水的速度为v,其航线恰好垂直于岸。由于雨季到来,水的流速增大了一些,为了保持航线不变,下列办法可行的是( )
A.减小θ角,增大船速 B.减小θ角,保持船速不变
C.增大θ角,保持船速不变 D.增大θ角,减小船速
如图所示,两个可视为质点的滑块a、b,通过铰链用长度为L的刚性轻杆相连接,a套在竖直杆A上,b套在水平杆B上,细杆A.B足够长,两杆分离不接触,且两杆间的距离很小可忽略不计。将滑块a从图示位置(轻杆与B杆夹角为30°)由静止释放,已知滑块a、b的质量均为m,重力加速度为g,不计一切摩擦。在此后的运动过程中,下列说法正确的是( )
A.滑块a的机械能守恒
B.滑块a运动到B杆所在高度时加速度为g
C.滑块b的最大速度为
D.当滑块a运动到B杆下方处时的速度为
如图,轻质不可伸长的细绳跨过光滑定滑轮C与质量为的物体A连接,A放在倾角为的固定光滑斜面上,绳的另一端和套在固定竖直杆上的物体B连接,BC连线恰好沿水平方向。若物体B从当前位置以速度匀速下滑,重力加速度大小为,设绳的张力大小为,在此后的运动过程中( )
A.物体A做匀速运动 B.物体A处于失重状态
C.物体A做加速运动 D.绳的张力大小大于
、解答题
炮筒与水平方向成30°角(图),炮弹从炮口射出时的速度大小是800 ,这个速度在水平方向和竖直方向的分速度各是多大?
汽艇以v1=18km/h的速度沿垂直于河岸的方向匀速向对岸行驶,河宽d=300m。
(1)设想河水不流动,汽艇驶到对岸要多长时间?
(2)如果河水流速为v2=3.6km/h,汽艇驶到对岸需要多长时间?汽艇在对岸何处靠岸?
5.2运动的合成和分解答案解析
、单选题
【答案】D
【解析】【解答】质点在F1的作用由静止开始从坐标系的原点O沿+x轴方向做匀加速运动,加速度
速度为v1=at1=4m/s
对应位移x1= a1t12=4m
到2s末撤去F1再受到沿+y方向的力F2的作用,物体在+x轴方向匀速运动x2=v1t2=4m
在+y方向加速运动,+y方向的加速度
方向向上,对应的位移
物体做曲线运动.q再根据曲线运动的加速度方向大致指向轨迹凹的一向,知D符合题意,ABC不符合题意。
故答案为:D
【分析】对物体进行受力分析,在x和y两个方向上,利用牛顿第二定律求解物体的加速度,利用运动学公式求解两个方向的位移,再合成即可。
【答案】D
【解析】【解答】小船在静水中的速度大小为2v,当船头指向始终与河岸垂直,则有: ;当回程时行驶路线与河岸垂直,而回头时的船的合速度为: ;则有: ;因此去程与回程所用时间之比为 :2,D符合题意,ABC不符合题意;
故答案为:D.
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】C
【解析】【解答】A.只要静水速度与河岸不平行,船就能渡过河.A不符合题意;
B.因船在静水中的速度4m/s大于水的速度3m/s,所以船能沿垂直于河岸方向过河,B不符合题意;
C.静水速与河岸垂直时,渡河时间最短,最短时间为 ,C符合题意
D.船头与河岸的夹角不同,船渡河的速度一般不同,所以船渡河的速度不一定为5m/s,D不符合题意;
故答案为:C。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】B
【解析】【解答】解:质点同时参与相互垂直的两个方向上的两个运动,由题意可知v0x=3m/s,v0y=4m/s, ,
合运动的初速度为:
方向与水平方向夹角为θ,则
解得:θ=53°
合运动的加速度为:
方向与水平方向夹角为α,则
解得:α=37°
综合上述比较可知:θ>α
合初速度与合加速度不在同一直线上,质点做曲线运动,并且弯向受力一侧,也就是合加速度方向,又因为合加速度是个恒量,所以B符合题意,ACD不符合题意。
故答案为:B。
【分析】结合水平方向的加速度和竖直方向的加速度,利用运动学公式求解位移,进而求解两个方向的合位移即可。
【答案】A
【解析】【解答】由题图可知,合速度的方向与船的速度方向的夹角越来越小,如图所示
又因为不变,故一直减小。
故答案为:A.
【分析】利用速度的分解结合速度的方向可以判别水流速度的大小变化。
【答案】A
【解析】【解答】设某时刻船速v1,绳子方向和船速夹角为α,则
所以当小船靠岸时,随α增大,船速逐渐增大,A符合题意,BCD不符合题意。
故答案为:A.
【分析】把小船的速度分解到沿绳子的速度和垂直于绳子的速度,其中沿绳子的速度等于自由端速度,再利用几何关系分析速度的变化,确定加速度的方向。
【答案】C
【解析】【解答】根据题意,船的实际速度是 和 的合速度, 与河岸平行,对渡河时间没有影响,所以 与河岸垂直即船头指向对岸时,渡河时间最短为 ,式中d为河宽,此时合速度与河岸成一定夹角,船的实际路线应为 所示;最短位移即为d,应使合速度垂直河岸,则 应指向河岸上游,实际路线为 所示,C符合题意,ABD不符合题意.
故答案为:C.
【分析】最短时间过河船身应垂直岸,对地轨迹应斜向下游;最短路程过河船身应斜向上游,而船相对岸的轨迹是垂直岸.
【答案】D
【解析】【解答】根据矢量的合成法则,当合速度方向与皮划艇相对静水的速度方向垂直时,皮划艇渡河的航程最短,则有
故答案为:D。
【分析】结合矢量的合成以匀速直线运动的规律得出 皮划艇渡河的最短航程 ,
【答案】A
【解析】【解答】小船的渡河时间只和河宽已经沿垂直河岸方向的速度 ,所以 。
故答案为:A.
【分析】看分运动,垂直河岸,根据时间公式列式,求解时间。
【答案】C
【解析】【解答】将B点的速度分解如右图所示,则有:
,
解得:
故答案为:C
【分析】根据运动的合成与分解,结合A的速度与B的速度沿着绳子方向的速度大小相等,结合平行四边形定则求出物体B的速度.
、多选题
【答案】A,B
【解析】【解答】由题图,可将船在静水中的速度分解在水平方向,则有
水的流速增大了,为保持航线不变,即合速度方向仍然保持垂直对岸。若减小θ角,增大船速或若减小θ角,保持船速不变均可达到上述目的;同理,若增大θ角,保持船速不变或增大θ角,减小船速,均不能达到上述目的。AB符合题意,CD不符合题意。
故答案为:AB。
【分析】根据合运动与分运动之间的关系,将船的运动分解为沿河方向的分运动和垂直河岸的分运动进行分析求解。
【答案】B,C
【解析】【解答】A.由于整个运动过程中没有摩擦阻力,因此系统机械能守恒,滑块a的机械能不守恒,A不符合题意;
B.滑块a运动到B杆所在高度时,滑块b速度为0,滑块a到达水平面,在竖直方向只受重力作用,则加速度为g,B符合题意;
C.当滑块a下降到最低点时,滑块a的速度为零,滑块b的速度最大,根据机械能守恒定律
解得
C符合题意;
D.当滑块a运动到B杆下方处时,由几何知识可知,ab与B杆夹角仍为30°,根据机械能守恒定律
滑块ab沿刚性轻杆方向速度相等,有
解得
D不符合题意。
故答案为:BC。
【分析】注意机械能守恒是系统机械能守恒,不是单独某物体机械能守恒。如果可以求出某方向的合力,可以结合牛顿第二定律求出该方向加速度。系统机械能守恒,一个物体机械能最小时另一个物体机械能最大。还要注意连接体沿杆方向速度相等,利用运动合成与分解,求出正确结果。
【答案】C,D
【解析】【解答】由题意可知,将B的实际运动,分解成两个分运动,如图所示
根据平行四边形定则,有
因物体B以速度匀速下滑,增大,所以物体A的速度增大,则物体A做加速运动,物体A有向上的加速度,处于超重状态,可得绳子对A的拉力一定大于A的重力沿斜面向下的分力,即
CD符合题意,AB不符合题意。
故答案为:CD。
【分析】将B的实际运动,根据平行四边形定则,分解成两个分运动。物体A有向上的加速度,处于超重状态。
、解答题
【答案】解:根据速度的合成与分解,可将炮弹从炮口射出时的速度可以分解为水平和竖直方向,则水平方向的分速度为
则竖直方向的分速度为
【解析】【分析】炮弹从炮口射出后做斜抛运动,利用速度的分解结合合速度的大小可以求出两个分速度的大小。
【答案】(1)解:由题可知
因为汽艇沿垂直于河岸的方向匀速向对岸行驶,所以汽艇驶到对岸的时间为
(2)解:由于运动具有独立性,当河水速度不为零时,过河时间不变,仍为
又因为运动具有同时性,所以汽艇在对岸靠岸时,沿岸边的水平距离为
其中
所以
【解析】【分析】(1)汽艇过河做匀速直线运动,利用位移公式可以汽艇过河的时间;
(2)当河水速度不为0时,利用河岸宽度及船速可以判别过河时间不变;结合沿平行河岸的位移公式可以求出其位移的大小。
第 1 页(共 1 页)
、单选题
光滑水平面上有一直角坐标系,质量m=4 kg的质点静止在坐标原点O处.先用沿x轴正方向的力F1=8 N作用了2 s;然后撤去F1,并立即用沿y轴正方向的力F2=24 N作用1 s,则质点在这3 s内的轨迹为图中的( ).
A. B.
C. D.
有一条两岸平直、河水均匀流动,流速恒为v的大河,一条小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直,小船在静水中的速度大小为2v,去程与回程所用时间之比为( )
A.3∶2 B.2∶1 C.3∶1 D.
一只小船在静水中的速度为4m/s,它要渡过40m宽的河,河水的速度为3m/s,则下列说法正确的是( )
A.船不能渡过河 B.船不能垂直到达对岸
C.船渡河的最短时间为10s D.船渡河的速度一定为5m/s
一质点同时参与相互垂直的x方向和y方向上的两个运动,已知t=0时刻,x方向上速度为3m/s,y方向上速度为4m/s;两个方向上的运动均为匀加速运动,x方向上的加速度为4m/s2,y方向上的加速度为3m/s2.下列哪个图能定性描述该质点的运动轨迹( )
A. B.
C. D.
小船横渡一条河,船头方向始终与河岸垂直,若小船相对静水的速度大小不变,运动轨迹如图所示,则河水的流速( )
A.由A到B水速逐渐减小 B.由A到B水速逐渐增大
C.由A到B水速先增大后减小 D.由A到B水速先减小后增大
用跨过定滑轮的绳把湖中小船拉靠岸,如图,已知拉绳的速度v不变,则船速( )
A.逐渐增大 B.不变
C.逐渐减小 D.先增大后减小
已知河水的流速为v1,小船在静水中的速度为v2,且v2>v1,下面用小箭头表示小船及船头的指向,则能正确反映小船在最短时间内渡河、最短位移渡河的情景图示依次是( )
A.①② B.①⑤ C.④⑤ D.②③
为了备战皮划艇比赛,某队员在河中进行训练。若河岸平直,河面宽,水流速度大小为,皮划艇相对静水的速度大小为,则皮划艇渡河的最短航程为()
A.
如图所示,河的宽度为d,船渡河时船头始终垂直河岸.若船在静水中的速度大小为v1,河水流速的大小为v2,则船渡河所用时间为( )
A.
如图所示,有两条位于同一竖直平面内的水平轨道,轨道上有两个物体A和B,它们通过一根绕过定滑轮O的不可伸长的轻绳相连接,物体A以速率=10m/s匀速运动,在绳与轨道成30°角时,物体B的速度大小为( )
A.5 m/s B. m/s C. m/s D.20 m/s
、多选题
如图所示,河的两岸是平行线,小船过河时,船头偏向上游与岸的夹角为θ,船相对于静水的速度为v,其航线恰好垂直于岸。由于雨季到来,水的流速增大了一些,为了保持航线不变,下列办法可行的是( )
A.减小θ角,增大船速 B.减小θ角,保持船速不变
C.增大θ角,保持船速不变 D.增大θ角,减小船速
如图所示,两个可视为质点的滑块a、b,通过铰链用长度为L的刚性轻杆相连接,a套在竖直杆A上,b套在水平杆B上,细杆A.B足够长,两杆分离不接触,且两杆间的距离很小可忽略不计。将滑块a从图示位置(轻杆与B杆夹角为30°)由静止释放,已知滑块a、b的质量均为m,重力加速度为g,不计一切摩擦。在此后的运动过程中,下列说法正确的是( )
A.滑块a的机械能守恒
B.滑块a运动到B杆所在高度时加速度为g
C.滑块b的最大速度为
D.当滑块a运动到B杆下方处时的速度为
如图,轻质不可伸长的细绳跨过光滑定滑轮C与质量为的物体A连接,A放在倾角为的固定光滑斜面上,绳的另一端和套在固定竖直杆上的物体B连接,BC连线恰好沿水平方向。若物体B从当前位置以速度匀速下滑,重力加速度大小为,设绳的张力大小为,在此后的运动过程中( )
A.物体A做匀速运动 B.物体A处于失重状态
C.物体A做加速运动 D.绳的张力大小大于
、解答题
炮筒与水平方向成30°角(图),炮弹从炮口射出时的速度大小是800 ,这个速度在水平方向和竖直方向的分速度各是多大?
汽艇以v1=18km/h的速度沿垂直于河岸的方向匀速向对岸行驶,河宽d=300m。
(1)设想河水不流动,汽艇驶到对岸要多长时间?
(2)如果河水流速为v2=3.6km/h,汽艇驶到对岸需要多长时间?汽艇在对岸何处靠岸?
5.2运动的合成和分解答案解析
、单选题
【答案】D
【解析】【解答】质点在F1的作用由静止开始从坐标系的原点O沿+x轴方向做匀加速运动,加速度
速度为v1=at1=4m/s
对应位移x1= a1t12=4m
到2s末撤去F1再受到沿+y方向的力F2的作用,物体在+x轴方向匀速运动x2=v1t2=4m
在+y方向加速运动,+y方向的加速度
方向向上,对应的位移
物体做曲线运动.q再根据曲线运动的加速度方向大致指向轨迹凹的一向,知D符合题意,ABC不符合题意。
故答案为:D
【分析】对物体进行受力分析,在x和y两个方向上,利用牛顿第二定律求解物体的加速度,利用运动学公式求解两个方向的位移,再合成即可。
【答案】D
【解析】【解答】小船在静水中的速度大小为2v,当船头指向始终与河岸垂直,则有: ;当回程时行驶路线与河岸垂直,而回头时的船的合速度为: ;则有: ;因此去程与回程所用时间之比为 :2,D符合题意,ABC不符合题意;
故答案为:D.
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】C
【解析】【解答】A.只要静水速度与河岸不平行,船就能渡过河.A不符合题意;
B.因船在静水中的速度4m/s大于水的速度3m/s,所以船能沿垂直于河岸方向过河,B不符合题意;
C.静水速与河岸垂直时,渡河时间最短,最短时间为 ,C符合题意
D.船头与河岸的夹角不同,船渡河的速度一般不同,所以船渡河的速度不一定为5m/s,D不符合题意;
故答案为:C。
【分析】当船速度与水流速度的合速度指向对岸时,此时过河所走的路程最短,求出合速度再除以河宽即可;如果船头始终垂直于河对岸,那么过河所用的时间最短,直接利用河宽除以船的速度即可。
【答案】B
【解析】【解答】解:质点同时参与相互垂直的两个方向上的两个运动,由题意可知v0x=3m/s,v0y=4m/s, ,
合运动的初速度为:
方向与水平方向夹角为θ,则
解得:θ=53°
合运动的加速度为:
方向与水平方向夹角为α,则
解得:α=37°
综合上述比较可知:θ>α
合初速度与合加速度不在同一直线上,质点做曲线运动,并且弯向受力一侧,也就是合加速度方向,又因为合加速度是个恒量,所以B符合题意,ACD不符合题意。
故答案为:B。
【分析】结合水平方向的加速度和竖直方向的加速度,利用运动学公式求解位移,进而求解两个方向的合位移即可。
【答案】A
【解析】【解答】由题图可知,合速度的方向与船的速度方向的夹角越来越小,如图所示
又因为不变,故一直减小。
故答案为:A.
【分析】利用速度的分解结合速度的方向可以判别水流速度的大小变化。
【答案】A
【解析】【解答】设某时刻船速v1,绳子方向和船速夹角为α,则
所以当小船靠岸时,随α增大,船速逐渐增大,A符合题意,BCD不符合题意。
故答案为:A.
【分析】把小船的速度分解到沿绳子的速度和垂直于绳子的速度,其中沿绳子的速度等于自由端速度,再利用几何关系分析速度的变化,确定加速度的方向。
【答案】C
【解析】【解答】根据题意,船的实际速度是 和 的合速度, 与河岸平行,对渡河时间没有影响,所以 与河岸垂直即船头指向对岸时,渡河时间最短为 ,式中d为河宽,此时合速度与河岸成一定夹角,船的实际路线应为 所示;最短位移即为d,应使合速度垂直河岸,则 应指向河岸上游,实际路线为 所示,C符合题意,ABD不符合题意.
故答案为:C.
【分析】最短时间过河船身应垂直岸,对地轨迹应斜向下游;最短路程过河船身应斜向上游,而船相对岸的轨迹是垂直岸.
【答案】D
【解析】【解答】根据矢量的合成法则,当合速度方向与皮划艇相对静水的速度方向垂直时,皮划艇渡河的航程最短,则有
故答案为:D。
【分析】结合矢量的合成以匀速直线运动的规律得出 皮划艇渡河的最短航程 ,
【答案】A
【解析】【解答】小船的渡河时间只和河宽已经沿垂直河岸方向的速度 ,所以 。
故答案为:A.
【分析】看分运动,垂直河岸,根据时间公式列式,求解时间。
【答案】C
【解析】【解答】将B点的速度分解如右图所示,则有:
,
解得:
故答案为:C
【分析】根据运动的合成与分解,结合A的速度与B的速度沿着绳子方向的速度大小相等,结合平行四边形定则求出物体B的速度.
、多选题
【答案】A,B
【解析】【解答】由题图,可将船在静水中的速度分解在水平方向,则有
水的流速增大了,为保持航线不变,即合速度方向仍然保持垂直对岸。若减小θ角,增大船速或若减小θ角,保持船速不变均可达到上述目的;同理,若增大θ角,保持船速不变或增大θ角,减小船速,均不能达到上述目的。AB符合题意,CD不符合题意。
故答案为:AB。
【分析】根据合运动与分运动之间的关系,将船的运动分解为沿河方向的分运动和垂直河岸的分运动进行分析求解。
【答案】B,C
【解析】【解答】A.由于整个运动过程中没有摩擦阻力,因此系统机械能守恒,滑块a的机械能不守恒,A不符合题意;
B.滑块a运动到B杆所在高度时,滑块b速度为0,滑块a到达水平面,在竖直方向只受重力作用,则加速度为g,B符合题意;
C.当滑块a下降到最低点时,滑块a的速度为零,滑块b的速度最大,根据机械能守恒定律
解得
C符合题意;
D.当滑块a运动到B杆下方处时,由几何知识可知,ab与B杆夹角仍为30°,根据机械能守恒定律
滑块ab沿刚性轻杆方向速度相等,有
解得
D不符合题意。
故答案为:BC。
【分析】注意机械能守恒是系统机械能守恒,不是单独某物体机械能守恒。如果可以求出某方向的合力,可以结合牛顿第二定律求出该方向加速度。系统机械能守恒,一个物体机械能最小时另一个物体机械能最大。还要注意连接体沿杆方向速度相等,利用运动合成与分解,求出正确结果。
【答案】C,D
【解析】【解答】由题意可知,将B的实际运动,分解成两个分运动,如图所示
根据平行四边形定则,有
因物体B以速度匀速下滑,增大,所以物体A的速度增大,则物体A做加速运动,物体A有向上的加速度,处于超重状态,可得绳子对A的拉力一定大于A的重力沿斜面向下的分力,即
CD符合题意,AB不符合题意。
故答案为:CD。
【分析】将B的实际运动,根据平行四边形定则,分解成两个分运动。物体A有向上的加速度,处于超重状态。
、解答题
【答案】解:根据速度的合成与分解,可将炮弹从炮口射出时的速度可以分解为水平和竖直方向,则水平方向的分速度为
则竖直方向的分速度为
【解析】【分析】炮弹从炮口射出后做斜抛运动,利用速度的分解结合合速度的大小可以求出两个分速度的大小。
【答案】(1)解:由题可知
因为汽艇沿垂直于河岸的方向匀速向对岸行驶,所以汽艇驶到对岸的时间为
(2)解:由于运动具有独立性,当河水速度不为零时,过河时间不变,仍为
又因为运动具有同时性,所以汽艇在对岸靠岸时,沿岸边的水平距离为
其中
所以
【解析】【分析】(1)汽艇过河做匀速直线运动,利用位移公式可以汽艇过河的时间;
(2)当河水速度不为0时,利用河岸宽度及船速可以判别过河时间不变;结合沿平行河岸的位移公式可以求出其位移的大小。
第 1 页(共 1 页)
