1.1周期变化课件-2022-2023学年高一下学期数学北师大版(2019)必修第二册(共24张PPT)
文档属性
| 名称 | 1.1周期变化课件-2022-2023学年高一下学期数学北师大版(2019)必修第二册(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 14:14:04 | ||
图片预览






文档简介
(共24张PPT)
第一章 三角函数
1.1 周期变化
1.通过生活实例及部分呈周期变化的函数,得到周期函数及周期、最小正周期的概念,并能认识三角函数是刻画周期现象的重要模型.
2.对周期变化的函数有初步的了解与认识,能够用数学刻画生活中的周期变化,用数学的观点和从数学的角度认识实际问题.
周期函数及周期的概念.
识别身边的周期现象,并用周期函数刻画周期现象.
“东升西落”
“昼夜循环”
“草枯草荣”
“冬去春来”
周而复始,始而复周的周期变化
在日常生活或是自然界中,你感受到了哪些周期变化的实例?请举例说明,并交流周期变化有哪些特征?
海水会发生潮汐现象,大约在每一昼夜的时间里,潮水会涨落两次,这是一种周期变化;钟表上的时针、分针和秒针每经过一周就会重复,这也是一种周期变化,周期变化是每隔一段时间就重复出现的变化.
我们怎样从数学的角度刻画周期变化呢?
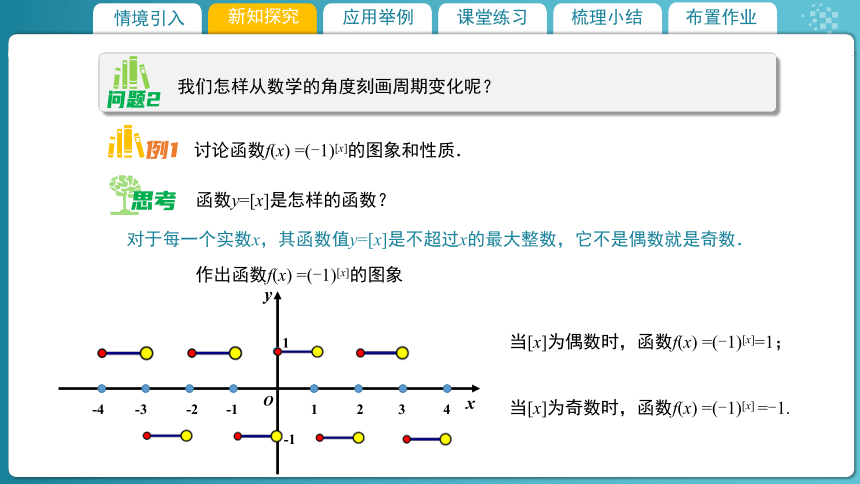
对于每一个实数x,其函数值y=[x]是不超过x的最大整数,它不是偶数就是奇数.
讨论函数f(x) =(-1)[x]的图象和性质.
函数y=[x]是怎样的函数?
作出函数f(x) =(-1)[x]的图象
4
3
2
1
-1
-2
-3
-4
1
-1
O
x
y
当[x]为偶数时,函数f(x) =(-1)[x]=1;
当[x]为奇数时,函数f(x) =(-1)[x] =-1.
根据图象,讨论函数f(x) =(-1)[x]的性质.
显然,对于任意一个实数x,每增加2的整数倍,其函数值保持不变,也就是说,在相同的“间隔”下,这种变化是重复进行的,所以函数f(x) =(-1)[x]变化是周期性的.
4
3
2
1
-1
-2
-3
-4
1
-1
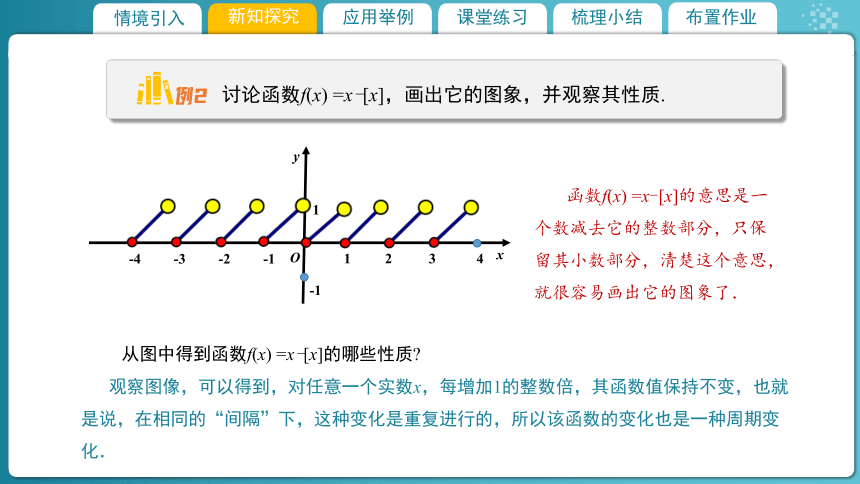
从图中得到函数f(x) =x-[x]的哪些性质
讨论函数f(x) =x-[x],画出它的图象,并观察其性质.
观察图像,可以得到,对任意一个实数x,每增加1的整数倍,其函数值保持不变,也就是说,在相同的“间隔”下,这种变化是重复进行的,所以该函数的变化也是一种周期变化.
函数f(x) =x-[x]的意思是一个数减去它的整数部分,只保留其小数部分,清楚这个意思,就很容易画出它的图象了.
O
x
y
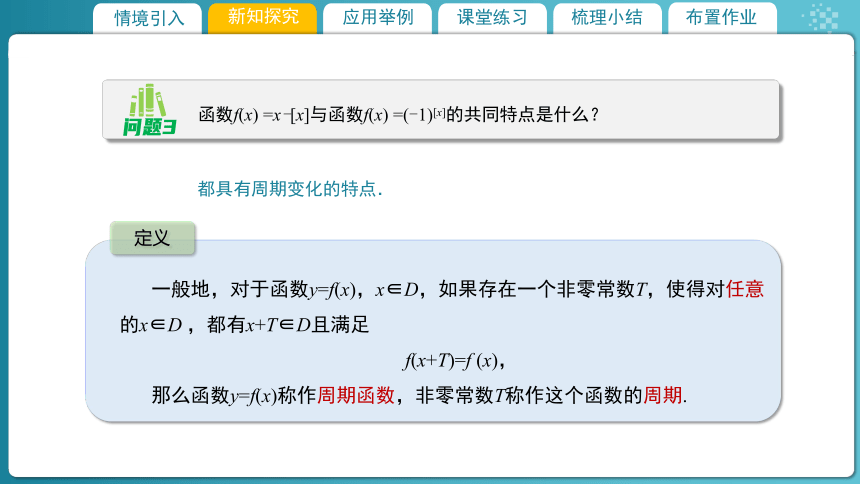
函数f(x) =x-[x]与函数f(x) =(-1)[x]的共同特点是什么?
都具有周期变化的特点.
定义
一般地,对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D ,都有x+T∈D且满足
f(x+T)=f (x),
那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.
如何理解概念中的“任意”?
周期函数定义中的“f(x+T)=f(x)”是对定义域中的每一个x值来说的,只有个别的x值满足f(x+T)=f(x),不能说T是y=f(x)的周期.
周期函数的周期是否只有一个
不是,比如对于例1中的函数f(x)=(-1)[x]来说,任何一个非零偶数都是它的周期.
对于例2中的函数f(x)=x- [x]来说,任何一个非零整数都是它的周期.
周期函数定义的实质:存在一个非零常数T,对定义域内的任意x,均有f(x+kT)=f(x),其中k∈Z,即自变量x每增加一个T后,函数值就会重复出现一次.
既然周期不唯一,如何选取某一个周期作为代表来表征函数的周期呢?
定义
如果在周期函数y=f(x)的所有周期中存在一个最小的正数,那么这个最小正数就称作函数y=f(x)的最小正周期.
若不加特别说明,本书所指周期均为函数的最小正周期.
判断(正确的打“√”,错误的打“×”) .
(1)若函数f(x)满足f(0)=f(5)=f(10),则它的周期T=5.( )
(2)若函数f(x)的周期T=5,则f(-5)=f(0)=f(5) .( )
(3)若函数f(x)为R上的奇函数,且f(x+2)=f(x),则f(2020)=0 .( )
概念辨析
(1)× (2)√ (3)√
讨论函数是否为周期函数,如果是,请指出它的周期.
解:当时,该函数的取值为8,6,8,6,8,…
可见它是周期函数,且周期T=2.
当给赋值,可以发现规律.
若对任意x∈R,函数f(x)满足f(x+2019)=-f(x+2020),求函数f(x)的周期.
解析:由f(x+2019)=-f(x+2020),
得f(x+2 019)=-f(x+2019+1)
令x+2 019=t,即f(t+1)=-f(t),
所以f(t+2)=f(t),
即函数f(x)的周期是2.
如何将f(x+2019)=-f(x+2020)形式转化为f(x+T)=f (x)的结构?
若对任意x∈R,函数f(x)满足 ,求函数f(x)的周期.
由 ,得 ,即 .
(1)若对任意,函数满足,则函数的周期T=?
(2)若对任意,函数满足,则函数的周期T=?
(3)若对任意,函数满足,则函数的周期T=?
(4)若对任意,函数满足,则函数的周期T=?
设定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+…+f(2018)=___________.
由f(x+2)=f(x),得函数f(x)的周期T=2.
又当x∈[0,2)时,f(x)=2x-x2,所以f(0)=0,f(1)=1,
所以f(0)=f(2)=f(4)=…=f(2 018)=0, f(1)=f(3)=f(5)=…=f(2 017)=1.
故 f(0)+f(1)+f(2)+…+f(2018)=1009.
由局部到整体
如何由x∈[0,2)扩充到整个定义域的函数值?
设定义在R上的函数f(x)满足f(x+3)=f(3),且f(x)为偶函数,若f(1)<1, ,求实数a的取值范围.
解:由f(x)为定义在R上的周期为3的偶函数,
得 f(5)=f(5-6)= f(-1)= f(1).
由f(1)<1, ,
得 .
解得 -1<a<4.
由于f(x)的周期由于f(x)的周期为5,且为奇函数,所以f(8)=f(5+3)=f(3)=f(5-2)=f(-2)=-f(2)=-2,f(4)=f(5-1)=f(-1)=-f(1)=-1,所以f(8)-f(4)=-2-(-1)=-1.
答案:A.
为5,且为奇函数,所以f(8)=f(5+3)=f(3)=f(5-2)=f(-2)=-f(2)=-2,f(4)=f(5-1)=f(-1)=-f(1)=-1,所以f(8)-f(4)=-2-(-1)=-1.
答案:A.
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(8)-f(4)的值为( )
A.-1 B.1 C.-2 D.2
解:由于f(x)的周期为5,且为奇函数,
所以f(8)=f(5+3)=f(3)=f(5-2)=f(-2)=-f(2)=-2,f(4)=f(5-1)=f(-1)=-f(1)=-1,
所以f(8)-f(4)=-2-(-1)=-1.
答案:A.
A
由f(x)=-f(x+2),得f(x+4)=f(x),所以函数f(x)是周期为4的周期函数,所以
f(2 019)=f(504×4+3)=f(3)=f(1+2)=-f(1)=-(2+0)=-2.
答案:D.
若定义在R上的函数f(x)满足f(x)=-f(x+2),当x∈(0,2]时,f(x)=2x+x,则f(2019)=( )
A.5 B.-5 C.2 D.-2
解:由f(x)=-f(x+2),得f(x+4)=f(x),所以函数f(x)是周期为4的周期函数,所以f(2019)=f(504×4+3)=f(3)=f(1+2)=-f(1)=-(2+0)=-2.
答案:D.
D
十字路口处红绿灯亮灭的情况如下:1 min亮绿灯,接着10 s亮黄灯,再接着1 min亮红灯,10 s亮黄灯,1 min亮绿灯……刚开始亮绿灯时,某人过路口,10 min后又回到此路口,此时应该亮 灯.
红绿灯的亮灭以140s为一个周期,600=140×4+40,所以是绿灯.
答案:绿灯.
绿
已知f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-2.5)= .
解:f(-2.5)=f(-0.5)=-f(0.5)=-0.5.
答案0.5.
0.5
一般地,对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D ,都有x+T∈D且满足
f(x+T)=f (x),
那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.
周期函数
最小正周期
如果在周期函数y=f(x)的所有周期中存在一个最小的正数,那么这个最小正数就称作函数y=f(x)的最小正周期.
周期函数、最小正周期的概念
周期变化
求周期函数的最小正周期
利用函数的周期性求值
教材第3页练习第1,2,3题;
第4页A组第2,3题,B组第1题.
再 见
第一章 三角函数
1.1 周期变化
1.通过生活实例及部分呈周期变化的函数,得到周期函数及周期、最小正周期的概念,并能认识三角函数是刻画周期现象的重要模型.
2.对周期变化的函数有初步的了解与认识,能够用数学刻画生活中的周期变化,用数学的观点和从数学的角度认识实际问题.
周期函数及周期的概念.
识别身边的周期现象,并用周期函数刻画周期现象.
“东升西落”
“昼夜循环”
“草枯草荣”
“冬去春来”
周而复始,始而复周的周期变化
在日常生活或是自然界中,你感受到了哪些周期变化的实例?请举例说明,并交流周期变化有哪些特征?
海水会发生潮汐现象,大约在每一昼夜的时间里,潮水会涨落两次,这是一种周期变化;钟表上的时针、分针和秒针每经过一周就会重复,这也是一种周期变化,周期变化是每隔一段时间就重复出现的变化.
我们怎样从数学的角度刻画周期变化呢?
对于每一个实数x,其函数值y=[x]是不超过x的最大整数,它不是偶数就是奇数.
讨论函数f(x) =(-1)[x]的图象和性质.
函数y=[x]是怎样的函数?
作出函数f(x) =(-1)[x]的图象
4
3
2
1
-1
-2
-3
-4
1
-1
O
x
y
当[x]为偶数时,函数f(x) =(-1)[x]=1;
当[x]为奇数时,函数f(x) =(-1)[x] =-1.
根据图象,讨论函数f(x) =(-1)[x]的性质.
显然,对于任意一个实数x,每增加2的整数倍,其函数值保持不变,也就是说,在相同的“间隔”下,这种变化是重复进行的,所以函数f(x) =(-1)[x]变化是周期性的.
4
3
2
1
-1
-2
-3
-4
1
-1
从图中得到函数f(x) =x-[x]的哪些性质
讨论函数f(x) =x-[x],画出它的图象,并观察其性质.
观察图像,可以得到,对任意一个实数x,每增加1的整数倍,其函数值保持不变,也就是说,在相同的“间隔”下,这种变化是重复进行的,所以该函数的变化也是一种周期变化.
函数f(x) =x-[x]的意思是一个数减去它的整数部分,只保留其小数部分,清楚这个意思,就很容易画出它的图象了.
O
x
y
函数f(x) =x-[x]与函数f(x) =(-1)[x]的共同特点是什么?
都具有周期变化的特点.
定义
一般地,对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D ,都有x+T∈D且满足
f(x+T)=f (x),
那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.
如何理解概念中的“任意”?
周期函数定义中的“f(x+T)=f(x)”是对定义域中的每一个x值来说的,只有个别的x值满足f(x+T)=f(x),不能说T是y=f(x)的周期.
周期函数的周期是否只有一个
不是,比如对于例1中的函数f(x)=(-1)[x]来说,任何一个非零偶数都是它的周期.
对于例2中的函数f(x)=x- [x]来说,任何一个非零整数都是它的周期.
周期函数定义的实质:存在一个非零常数T,对定义域内的任意x,均有f(x+kT)=f(x),其中k∈Z,即自变量x每增加一个T后,函数值就会重复出现一次.
既然周期不唯一,如何选取某一个周期作为代表来表征函数的周期呢?
定义
如果在周期函数y=f(x)的所有周期中存在一个最小的正数,那么这个最小正数就称作函数y=f(x)的最小正周期.
若不加特别说明,本书所指周期均为函数的最小正周期.
判断(正确的打“√”,错误的打“×”) .
(1)若函数f(x)满足f(0)=f(5)=f(10),则它的周期T=5.( )
(2)若函数f(x)的周期T=5,则f(-5)=f(0)=f(5) .( )
(3)若函数f(x)为R上的奇函数,且f(x+2)=f(x),则f(2020)=0 .( )
概念辨析
(1)× (2)√ (3)√
讨论函数是否为周期函数,如果是,请指出它的周期.
解:当时,该函数的取值为8,6,8,6,8,…
可见它是周期函数,且周期T=2.
当给赋值,可以发现规律.
若对任意x∈R,函数f(x)满足f(x+2019)=-f(x+2020),求函数f(x)的周期.
解析:由f(x+2019)=-f(x+2020),
得f(x+2 019)=-f(x+2019+1)
令x+2 019=t,即f(t+1)=-f(t),
所以f(t+2)=f(t),
即函数f(x)的周期是2.
如何将f(x+2019)=-f(x+2020)形式转化为f(x+T)=f (x)的结构?
若对任意x∈R,函数f(x)满足 ,求函数f(x)的周期.
由 ,得 ,即 .
(1)若对任意,函数满足,则函数的周期T=?
(2)若对任意,函数满足,则函数的周期T=?
(3)若对任意,函数满足,则函数的周期T=?
(4)若对任意,函数满足,则函数的周期T=?
设定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+…+f(2018)=___________.
由f(x+2)=f(x),得函数f(x)的周期T=2.
又当x∈[0,2)时,f(x)=2x-x2,所以f(0)=0,f(1)=1,
所以f(0)=f(2)=f(4)=…=f(2 018)=0, f(1)=f(3)=f(5)=…=f(2 017)=1.
故 f(0)+f(1)+f(2)+…+f(2018)=1009.
由局部到整体
如何由x∈[0,2)扩充到整个定义域的函数值?
设定义在R上的函数f(x)满足f(x+3)=f(3),且f(x)为偶函数,若f(1)<1, ,求实数a的取值范围.
解:由f(x)为定义在R上的周期为3的偶函数,
得 f(5)=f(5-6)= f(-1)= f(1).
由f(1)<1, ,
得 .
解得 -1<a<4.
由于f(x)的周期由于f(x)的周期为5,且为奇函数,所以f(8)=f(5+3)=f(3)=f(5-2)=f(-2)=-f(2)=-2,f(4)=f(5-1)=f(-1)=-f(1)=-1,所以f(8)-f(4)=-2-(-1)=-1.
答案:A.
为5,且为奇函数,所以f(8)=f(5+3)=f(3)=f(5-2)=f(-2)=-f(2)=-2,f(4)=f(5-1)=f(-1)=-f(1)=-1,所以f(8)-f(4)=-2-(-1)=-1.
答案:A.
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(8)-f(4)的值为( )
A.-1 B.1 C.-2 D.2
解:由于f(x)的周期为5,且为奇函数,
所以f(8)=f(5+3)=f(3)=f(5-2)=f(-2)=-f(2)=-2,f(4)=f(5-1)=f(-1)=-f(1)=-1,
所以f(8)-f(4)=-2-(-1)=-1.
答案:A.
A
由f(x)=-f(x+2),得f(x+4)=f(x),所以函数f(x)是周期为4的周期函数,所以
f(2 019)=f(504×4+3)=f(3)=f(1+2)=-f(1)=-(2+0)=-2.
答案:D.
若定义在R上的函数f(x)满足f(x)=-f(x+2),当x∈(0,2]时,f(x)=2x+x,则f(2019)=( )
A.5 B.-5 C.2 D.-2
解:由f(x)=-f(x+2),得f(x+4)=f(x),所以函数f(x)是周期为4的周期函数,所以f(2019)=f(504×4+3)=f(3)=f(1+2)=-f(1)=-(2+0)=-2.
答案:D.
D
十字路口处红绿灯亮灭的情况如下:1 min亮绿灯,接着10 s亮黄灯,再接着1 min亮红灯,10 s亮黄灯,1 min亮绿灯……刚开始亮绿灯时,某人过路口,10 min后又回到此路口,此时应该亮 灯.
红绿灯的亮灭以140s为一个周期,600=140×4+40,所以是绿灯.
答案:绿灯.
绿
已知f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-2.5)= .
解:f(-2.5)=f(-0.5)=-f(0.5)=-0.5.
答案0.5.
0.5
一般地,对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D ,都有x+T∈D且满足
f(x+T)=f (x),
那么函数y=f(x)称作周期函数,非零常数T称作这个函数的周期.
周期函数
最小正周期
如果在周期函数y=f(x)的所有周期中存在一个最小的正数,那么这个最小正数就称作函数y=f(x)的最小正周期.
周期函数、最小正周期的概念
周期变化
求周期函数的最小正周期
利用函数的周期性求值
教材第3页练习第1,2,3题;
第4页A组第2,3题,B组第1题.
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
